The Joule-Thomson effect describes the decrease in temperature of real gases when they expand against a lower pressure!
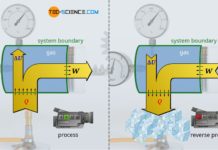
In the article Free expansion of an ideal gas in a vacuum it was explained that the free expansion of a gas against a vacuum taking place in an (ideal) adiabatic system is an isothermal process. For this purpose, a gas-filled cylinder was considered, which is closed with a massless and frictionless sliding piston.

The temperature of the ideal gas remains constant during such an adiabatic expansion. However, this applies only to ideal gases. If, on the other hand, such an experiment is carried out with a real gas, then a slight decrease in temperature would be observed in reality (even though the piston can still be considered to be massless). This phenomenon is due to the attractive forces acting between the gas molecules, which are neglected in the case of ideal gases.
Because when a real gas expands, the distances between the molecules increase due to the increasing volume. The gas must therefore increase its volume against the attractive forces acting between the molecules. This process obviously requires energy. This energy must be delivered by the gas itself and can only be provided at the expense of the kinetic energy of the gas molecules. This means a decrease in temperature, because the temperature is directly linked to the kinetic energy. This phenomenon does not only occur during the expansion against a vacuum, but ultimately whenever a real gas expands against a lower pressure. This effect of temperature decrease is also called Joule-Thomson effect.
The Joule-Thomson effect is the phenomenon of a decrease in temperature of real gases when they expand against a lower pressure!
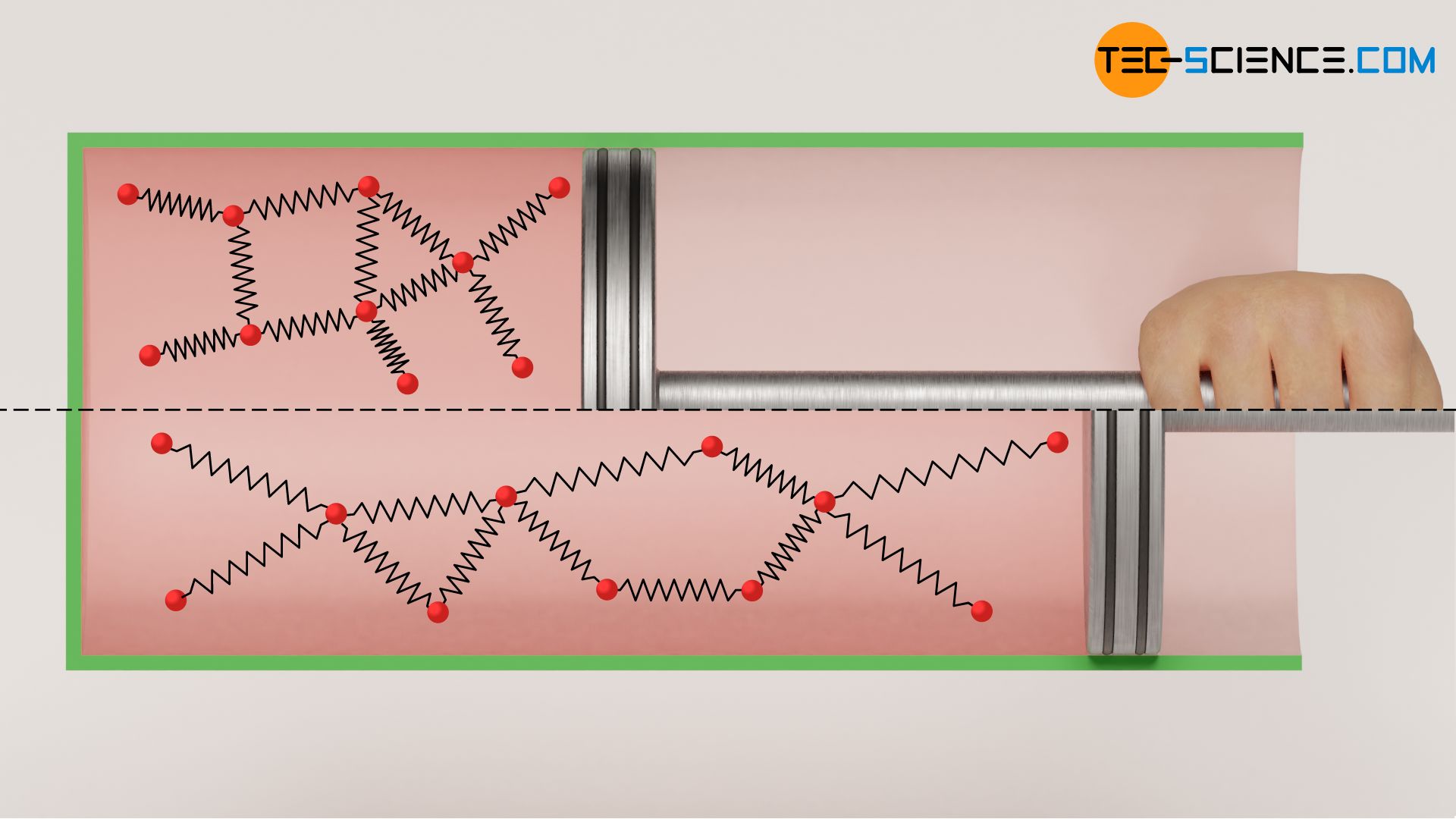
Note that in many cases the gas temperature decreases during an expansion. This generally has nothing to do with the Joule-Thomson effect. The Joule-Thomson effect only describes the stronger decrease in temperature for real gases than would be the case for ideal gases, since binding energies must be taken into account for real gases. And as already explained, these binding energies cause an additional amount of work during an expansion, which is at the expense of the kinetic energies, which additionally decreases the temperature. Only this additional temperature decrease is called the Joule-Thomson effect.
Note also that even with an adiabatic (!) expansion of a real gas against a vacuum, the internal energy of the gas remains constant. In a real gas, the internal energy is not only composed of the kinetic energy of the molecules as in an ideal gas, but also binding energies are part of the internal energy. In real gases, there is only an “internal” redistribution of energies, namely at the expense of the kinetic energy and in favor of the binding energies. The work done by the gas to increase the molecular distances is not transferred across the system boundary, but only redistributed internally!
The first law of thermodynamics only balances energies that are tranferred accross the system boundary! In an adiabatic expansion against a vacuum, neither such boundary work nor heat is transferred (W=0, Q=0)! Thus, even for real gases, there is no change in the internal energy ΔU:
\begin{align}
\underbrace{W}_{=0} + \underbrace{Q}_{=0} = \Delta U = 0
\end{align}