Heat transfer by thermal conduction means that heat is conducted through a material. Heat energy is transferred from molecule to molecule at the atomic level.
Introduction
The principle of thermal convection can basically only occur in materials that have the ability to flow. This applies therefore only to liquids and gases (fluids). In solids, however, the molecules are bound to a certain location and therefore cannot flow. Heat transport by convection is therefore not possible in solids.
The figure below show thermal images of a building and a cup of hot tea. It can be seen that heat is obviously also transported by such solids and heat is transferred from the inside to the outside. So there must be another mechanism for heat transfer besides convection.

Experiment on thermal conduction
To demonstrate this new mechanism of heat transfer, a metal bar is attached horizontally to a tripod. A Bunsen burner is now placed under the bar at point A, while a thermometer is attached to the end of the bar at point B. Additionally, there are drops of wax on the bar at smaller distances. When the Bunsen burner is turned on, after a short time one can observe how the wax drops liquefy and drip off the bar, while the temperature at the thermometer gradually increases.
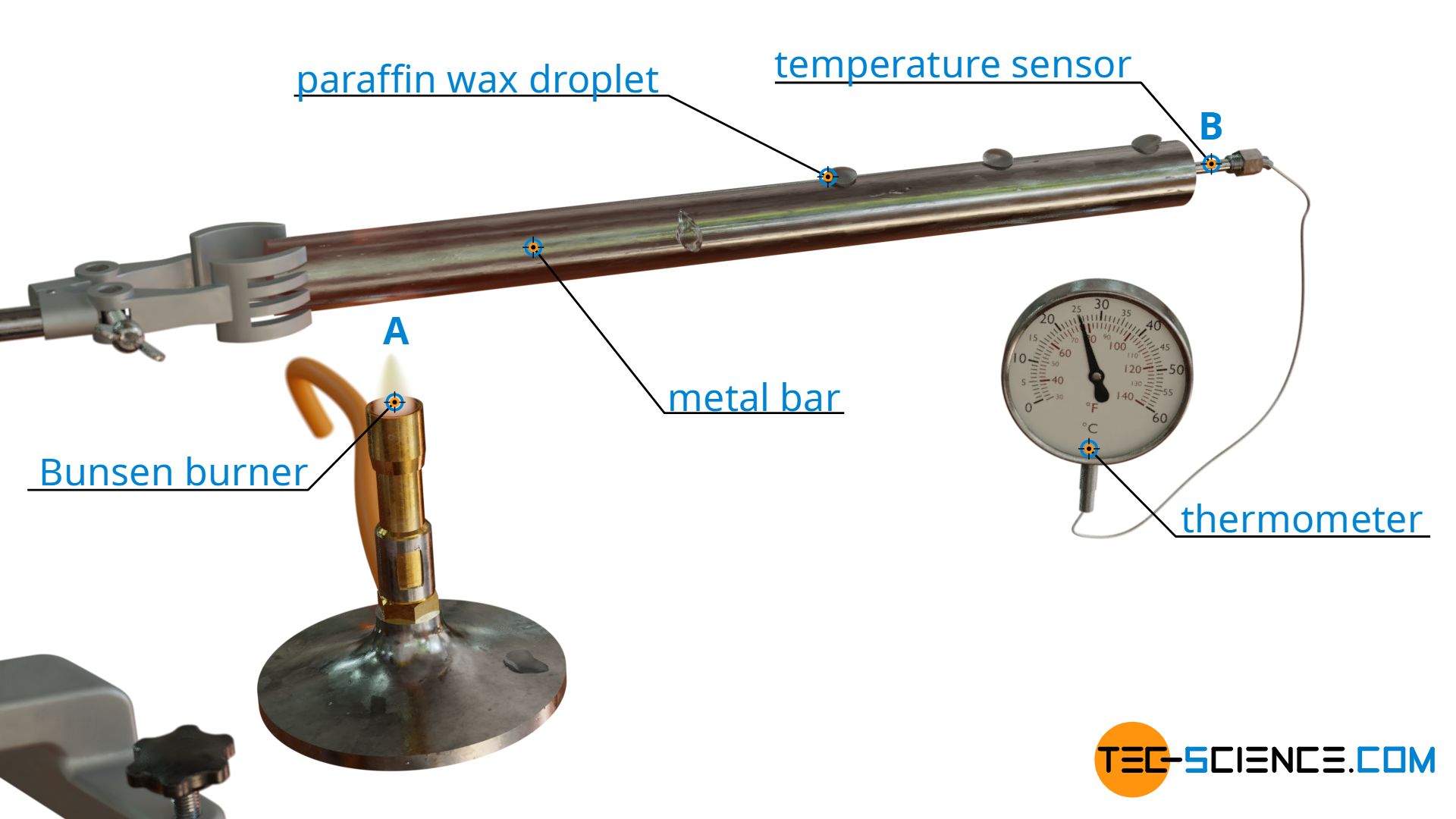
Obviously heat energy was transported from heat source A (Bunsen burner) to point B (thermometer) to cause this temperature increase. Unlike the heat flow, however, the “hot” particles did not move macroscopically from A to B. After all, in a solid body the particles are bound to a fixed location and cannot move freely as in liquids or gases. This can also be seen in the wax drops, which melt at a fixed location and do not move from the actual location during the heat transfer.
In this case, the heat transfer took place through the elastic bonding forces between the particles, which are similar to a spring. This is because if one particle is set in oscillation at a certain point, the neighbouring particles will also be set in oscillation by the elastic bond. In thermal conduction, heat energy can thus be transferred from particle to particle without the particles moving macroscopically from the location as is the case with thermal convection.
Thermal conduction does not necessarily require the presence of binding forces between the individual particles. Energy can also be transferred from one molecule to another molecule by direct collisions. In this way too, energy can be transported over long distances without the individual particles themselves moving over greater distances. Thermal conduction therefore occurs not only in solids, but also in liquids or gases. More about this later.
Conclusion and illustration
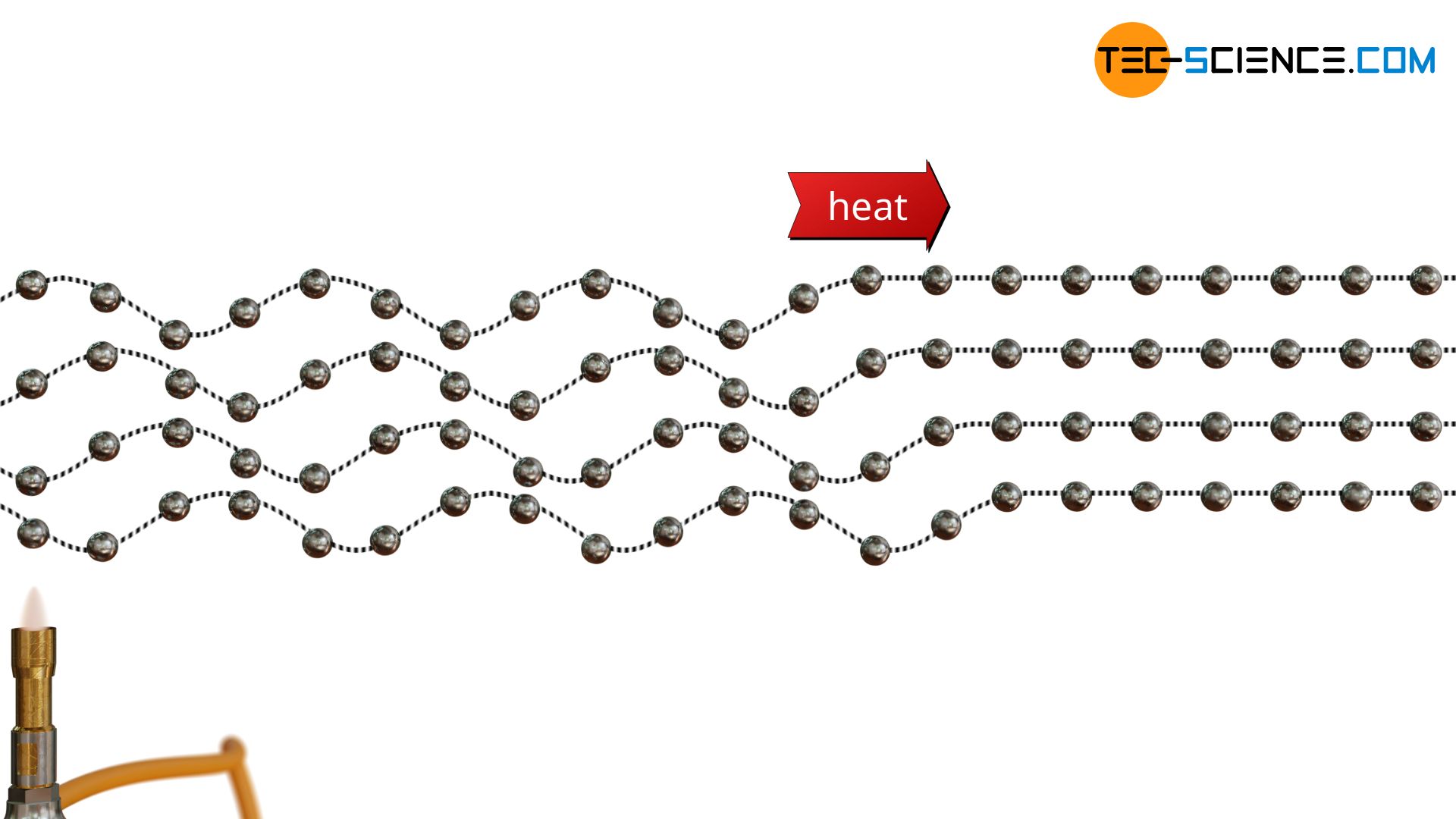
This principle of transferring the heat energy from particle to particle without moving over long distances is called thermal conduction. Heat is conducted through the material, so to speak. The animation below illustrates the principle of thermal conduction, in which heat is transferred from molecule to molecule without the molecules moving themselves.
In heat transport by conduction, heat is passed through the material without the particles moving macroscopically.
How well or poorly an object conducts heat varies from material to material. Physically, this property is described by the so-called thermal conductivity, which due to its complexity is discussed in more detail in a separate article. In the following sections, however, the physical cause of the different thermal conductivities will be dealt with in more detail.
Thermal conductivity in insulators
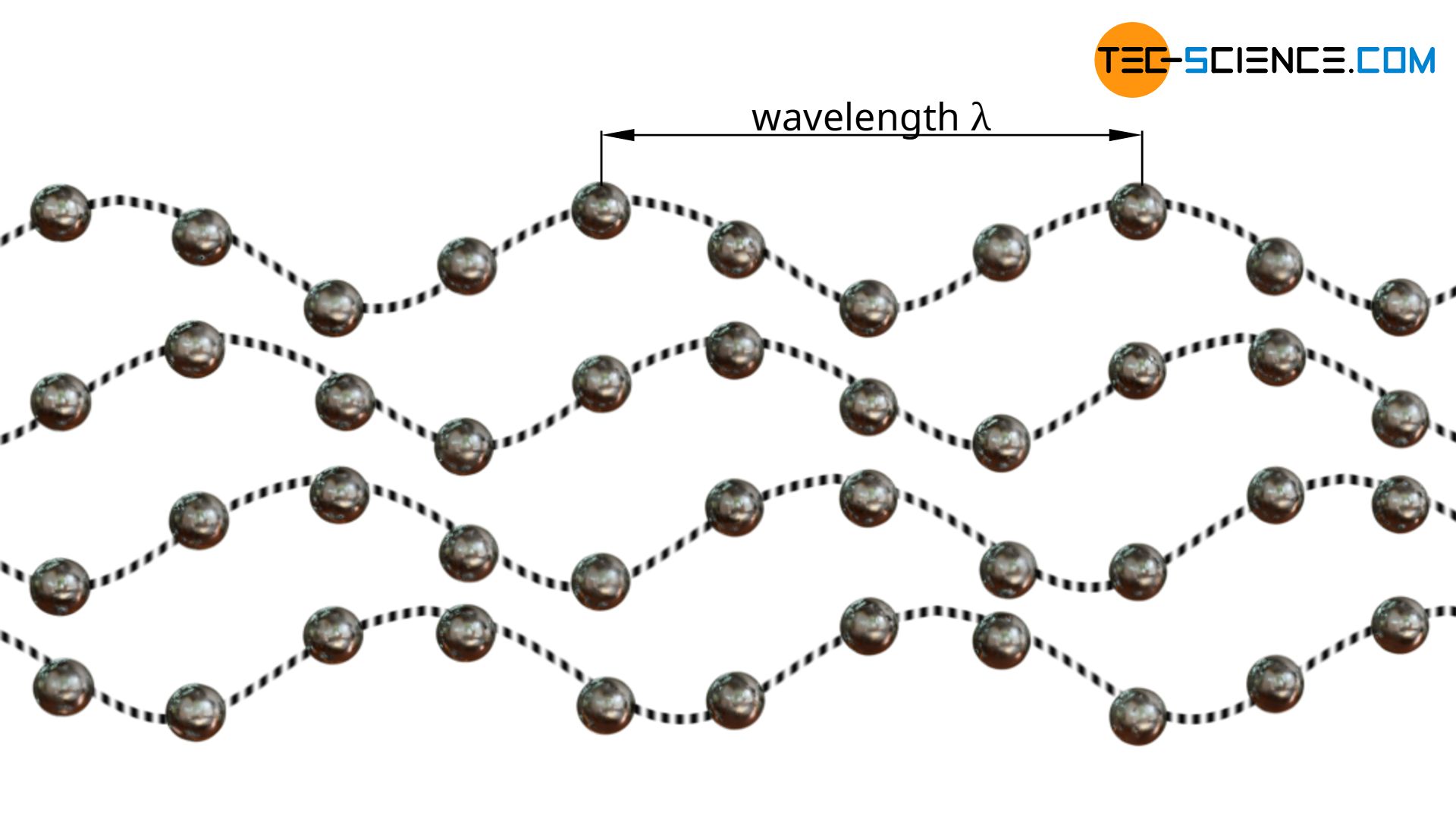
As already mentioned, heat transfer in solids occurs due to oscillations of the atoms. For this purpose, one can imagine the atoms as balls attached to a rubber cord at regular intervals. If one ball is now set in oscillation, the neighboring ball also begins to oscillate due to the elastic bond. The vibrational energy is thus transferred from ball to ball. Finally a kind of wave is formed which transports (heat) energy.
In solids, if the particles of a substance are very close to each other, energy can be transferred from one particle to the neighboring particle relatively quickly due to the stronger binding forces (“rigid connection”). One can again imagine the atoms as balls. However, instead of attaching the balls to an extremely elastic rubber cord, they are now mounted at small distances on a relatively rigid rod. If the first ball is now set in vibration, the neighbouring ball is set in vibration practically at the same moment. The vibrational energy thus spreads extremely quickly from ball to ball. If the balls are also relatively light, they can also be made to vibrate quickly. Both together (strong bonding forces and light particles) thus lead to good heat conduction.
Solids consisting of light particles with a high particle density generally have a high thermal conductivity!
The oscillations of the atoms ultimately represent waves that propagate within the solid body at the speed of sound. According to quantum mechanics, such waves can also be understood as particles with an impulse (wave-particle duality). The momentum of the particle corresponds to the momentum of the original wave. In this way, thermal conduction in solids can also be described by the movement/collision of “classical” particles, as is the case in gases or liquids. The atom waves imagined as particles are also called phonons (not to be confused with photons; these are the particles of an electromagnetic wave!)
In the same way that electromagnetic waves can be described by particles (called photons), lattice waves can also be described by particles (called phonons).
With the help of the model of the phonons, a uniform basis is thus obtained on which all thermal conduction is described: by collisions of particles! Just as “real” particles of gases or liquids transfer heat energy by collisions, with the phonon model energy is also transferred by collisions, i.e. by collisions of phonons.
Thermal conduction in metals
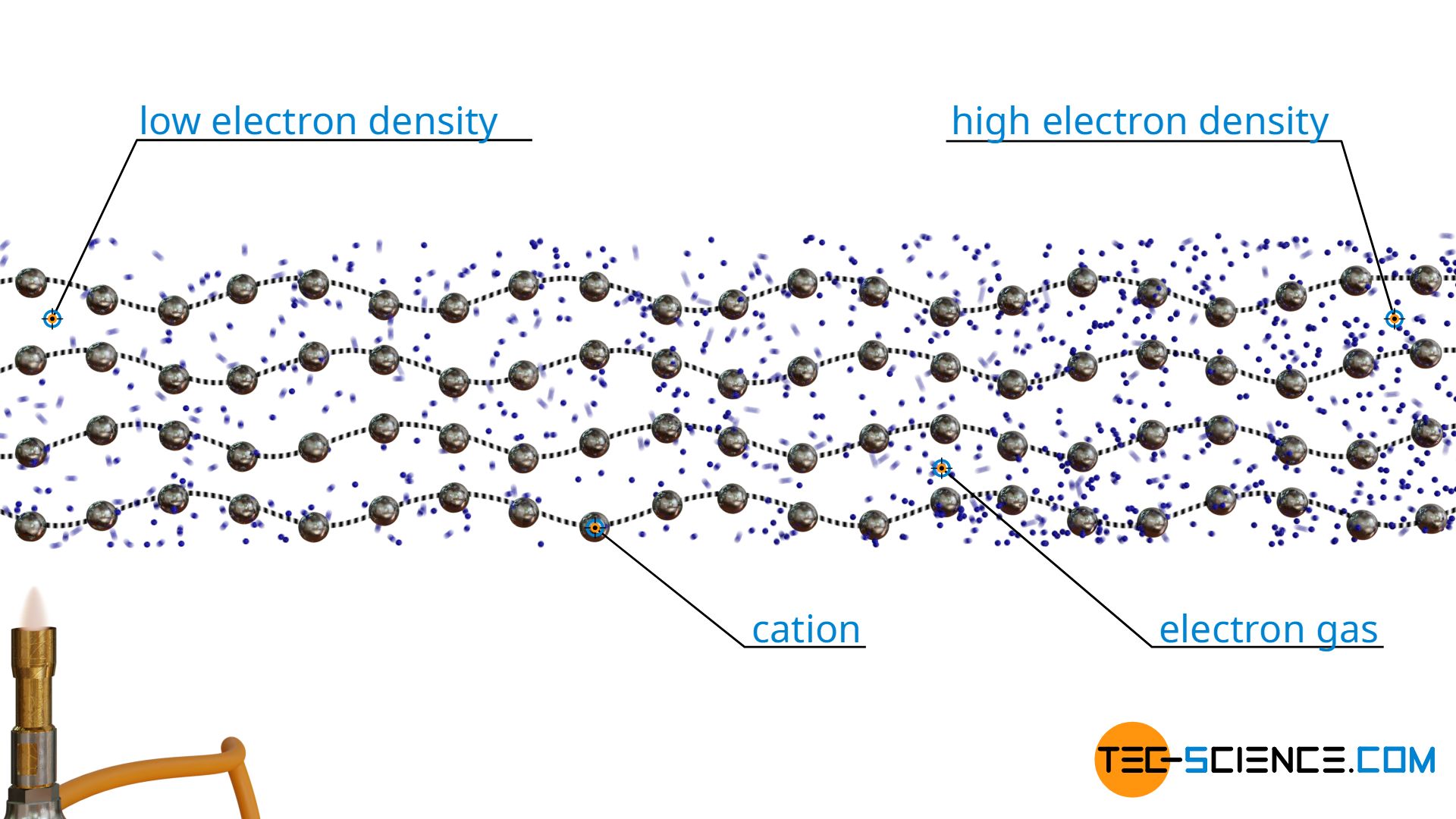
In metals, thermal conduction is not only caused by the oscillation of the atoms (i.e. by phonons), but mainly by the free electrons of the electron gas. The electrons are able to transfer their energy by collisions with other electrons. They thus also take part in heat transport, and to a much greater extent than the lattice vibrations.
Due to the large number of free electrons, metals are therefore not only very good conductors of electricity, but also very good conductors of heat! Especially graphene, as the only electrically conductive non-metal, has an extremely high thermal conductivity due to the large number of free electrons present. Graphene exceeds the thermal conductivity of steel, for example, by more than a hundred times!
At this point, another phenomenon appears in addition to the good heat conduction of metals. Due to the strong thermal motion of the electrons, the electron gas has a lower density near the heat source than at a greater distance from it, where the temperature and thus the thermal motion is lower. This charge difference ultimately leads to a voltage. The resulting voltage along the temperature gradient is also called the Seebeck effect. Conversely, the temperature difference can be deduced from the Seebeck effect or the resulting voltage. This principle is used in thermocouples for measuring temperatures.
The relatively high thermal conductivity of metals is used wherever heat needs to be transported as quickly as possible. This is the case for example in cooling applications. The figure below shows a graphics card. The metal heat sink absorbs the heat from the underlying chip and conducts it to the cooling fins as quickly as possible. The airflow caused by the fan then transports the heat away by convection.
Another example where high thermal conductivity is required is the radiator. The heat given off by the circulating water should be transferred to the room air as quickly as possible. It should therefore pass through the radiator relatively quickly. This is why the high thermal conductivity of metals is also used there and radiators are made of metal and not plastic.

Thermal conduction in gases
Compared to solids, gases usually show low thermal conductivites. This is because gases have only a relatively low number of molecules. However, since thermal conduction is based on the transfer of energy from molecule to molecule, only little energy can be transported when only a few molecules are present.
In fact, however, for ideal gases the thermal conductivity is independent of pressure, i.e. independent of particle density! This seems to contradict the statement just made that density has an influence on thermal conductivity. In ideal gases, however, the thermal conductivity is independent of particle density because, to the same extent as the heat-conducting particles increase due to a higher density, the mean free path decreases! The many particles stand in their own way, so to speak, and hinder each other in thermal conduction. More about this in the article Thermal conductivity of gases.
The independence of thermal conductivity from gas pressure is only valid up to a certain extent. At very low pressures the situation changes. If there are no particles at all in a gas, then of course no energy can be transferred from particle to particle and thus no heat can be transported. The thermal conductivity in a vacuum is therefore zero. In this case, heat transfer can only take place through thermal radiation. This is used, for example, in double-walled vacuum flasks, which contain a vacuum in between to prevent heat conduction.
The low thermal conductivity of gases is also used in construction engineering. In particular, air is often used for the thermal insulation of buildings. For example, panels made of foamed polystyrene (“Styrofoam”), which consists of over 98 % air. Because the air is firmly enclosed in the hollow spaces of the polystyrene, heat transport by convection is minimised at the same time.

Thermal conduction in liquids
In terms of particle density and the magnitude of the binding forces, the properties of liquids are between those of solids and gases. This is also reflected in the thermal conductivity. Therefore, liquids show significantly lower thermal conductivities compared to solids, but slightly higher thermal conductivities compared to gases.
The relatively low thermal conductivity of liquids compared to solids is also clearly demonstrated by the example of water. As already explained in the article Heat transfer by thermal convection, water is an excellent fluid when it comes to heat transport by convection. However, when it comes to thermal conductivity, water is actually a relatively poor conductor of heat. The relatively low thermal conductivity of water can be impressively demonstrated in a simple experiment. For this purpose, an ice cube is placed in a water-filled test tube. The ice cube is pressed against the bottom of the test tube with a small spiral spring so that it float to to the top.

If one now heats the upper part of the test tube with a Bunsen burner, the water there begins to boil. The ice cube, on the other hand, remains solid for a relatively long time, i.e. the water hardly heats up there. This shows that only little heat is conducted by the water to the ice cube.
The ice cube must therefore be at the bottom of the test tube, otherwise convection currents would form when the water is heated at the bottom. The warm water would then rise to the top and mix with the cold water. However, this would then no longer correspond to pure thermal conduction but to a thermal convection. By attaching the ice cube to the bottom, it should therefore be ensured that the heat transfer is mainly due to heat conduction.








