Der Druck beschreibt die Kraftverteilung auf einer Fläche und ist somit ein Maß für Stärke mit der eine Fläche belastet wird!
Definition
Im Alltag begegnet einem häufig der Begriff des Drucks. Beim Backen drückt man mit den Fingern in den Teig um ihn durchzukneten. Die Füße eines schweren Tisches drücken auf den relativ weichen Holzboden und hinterlassen unschöne Abdrücke. Eine Reißzwecke wird in eine Wand gedrückt um ein Plakat aufzuhängen.
Diese Beispiele zeigen, dass ein Druck offensichtlich immer nur dann entsteht, wenn mindestens zwei Gegenstände beteiligt sind (Finger-Teig, Tischfuß-Boden, Reißzwecke-Wand) und aufeinander Kräfte ausüben. Die Druckwirkung entsteht dabei immer an den unmittelbaren Berührungsflächen der beiden Gegenstände.

Aber nicht nur die Kraft ist für die Stärke einer Druckwirkung entscheidend. Hält man bspw. eine Reißzwecke zwischen Daumen und Zeigefinger, so wird man beim Zusammendrücken sehr rasch Unterschiede feststellen, und das obwohl beide Seiten offensichtlich mit derselben Kraft zusammengedrückt werden. Die Spitze der Reißzwecke drückt wesentlich schmerzhafter auf die Haut als der gegenüberliegende Kopf.

Auch die hinterlassenen Druckstellen der Füße des Tisches auf einem Holzboden werden umso tiefer sein, um so kleiner die Auflagefläche ist. Neben der Kraft ist also auch die Größe der Fläche für die Stärke der Druckwirkung entscheidend.
Die Alltagserfahrung zeigt, dass die Druckwirkung umso größer ist …
- je größer die Druckkraft und
- je geringer die Druckfläche ist.
Sinnvollerweise definiert man die Stärke einer Druckwirkung deshalb als Quotient aus Kraft F und Fläche A. Diese Druckwirkung wird kurz als Druck p bezeichnet.
\begin{align}
\label{p}
&\boxed{p =\frac{F}{A}}~~~~~[p]=\frac{\text{N}}{\text{m²}}=\text{Pa}~~~\text{(Pascal)} \\[5px]
\end{align}
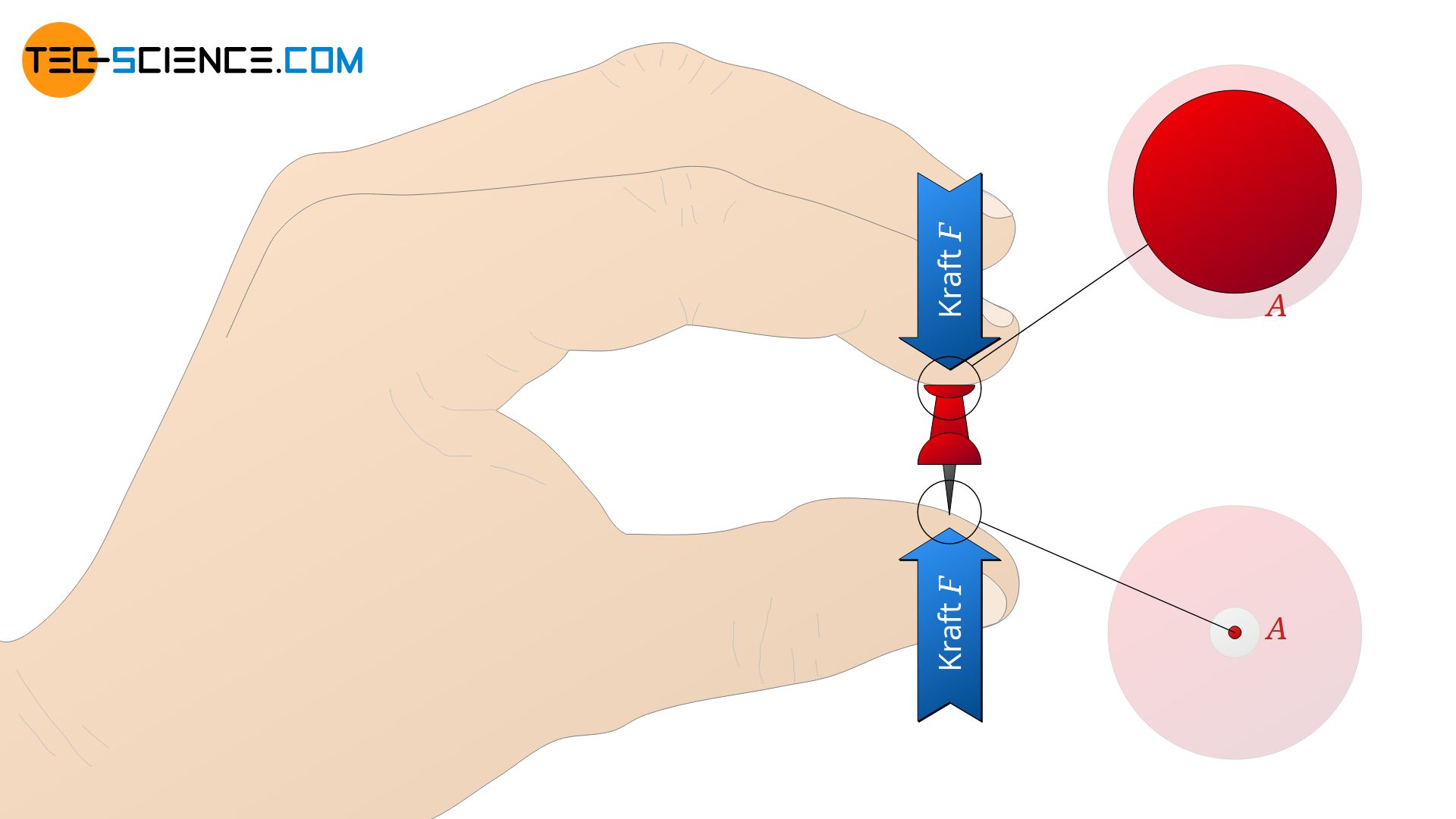
Der Druck beschreibt somit anschaulich die Kraftverteilung auf einer Fläche (Kraft pro Flächeneinheit) und besitzt entsprechend die Einheit N/m². Diese Einheit wird oft auch als Pascal „Pa“ bezeichnet. So bedeutet bspw. ein Druck von 300 N/m², dass pro Quadratmeter Fläche eine Kraft von 300 N wirkt.
Der Druck beschreibt die Kraftverteilung auf einer Fläche und ist somit ein Maß für Stärke mit der eine Fläche belastet wird!
Druck in Flüssigkeiten und Gasen
Bei den oben genannten Beispielen handelt es sich stets um feste Gegenstände, die Drücke aufeinander ausübten. Man spricht in diesem Zusammenhang auch vom sogenannten Auflagedruck. Aber nicht nur feste Körper können auf andere feste Gegenstände Kräfte und damit je nach Kontaktfläche entsprechende Drücke ausüben. Auch Gase und Flüssigkeiten üben auf Grenzflächen Kräfte und somit Drücke aus. Man spricht dann von Gasdrücken bzw. Flüssigkeitsdrücken.
Die Druckwirkung eines Gases zeigt sich zum Beispiel beim Aufpumpen eines Autoreifens. Die Luft ist offensichtlich in der Lage das Auto beim Aufpumpen etwas anzuheben. Die notwendige Kraft ergibt sich aus dem Luftdruck/Gasdruck im Reifen. Auch Flüssigkeiten sind in der Lage Kräfte und damit Drücke auszuüben. Man denke bspw. an das Hydrauliköl eines Wagenhebers, durch dessen Druck ein Kolben mit großer Kraft angehoben wird.
Im Gegensatz zum Auflagedruck der salopp formuliert in eine bestimmte Richtung wirkt, ist die Druckwirkung von Gasen oder auch von Flüssigkeiten in alle Richtungen gleich. Auf diese Weise ist bspw. der Gasdruck eines Autoreifen in der Lage den Reifen in jede Richtung stabil in der Form zu halten. Auch der Druck in einer Flüssigkeit wird in alle Richtungen gleichermaßen wirken.

Im Gegensatz zu Auflagedrücken von festen Gegenständen, wirken die Drücke in Gasen oder Flüssigkeiten in alle Richtungen gleichermaßen!
Dass der Druck in Flüssigkeiten und Gasen in alle Richtungen gleichermaßen wirkt, kann man durch folgendes Experiment leicht nachweisen. Hierzu wird ein Kissen aus Gummi mit Wasser gefüllt. An verschiedenen Stellen des Kissens sind Schläuche angebracht. Am anderen Ende der Schläuche befinden sich Druckmessgeräte. Nun drückt man an einer beliebigen Stelle das Kissen zusammen. Man wird dabei feststellen, dass nicht nur der Druck in der Nähe der Druckstelle ansteigt, sondern alle Druckmesser gleichermaßen. Offensichtlich ist der Druck an allen Stellen der Flüssigkeit gleich groß. Anstelle von Wasser kann man den Versuch auch mit Gas durchführen, z.B. mit Luft. Das Ergebnis wird dasselbe sein.

Dass der Druck in Flüssigkeiten und Gasen in alle Richtungen gleichermaßen wirkt, ist der relativ freien Beweglichkeit der darin enthaltenen Teilchen geschuldet. Da die Teilchen keine bevorzugte Bewegungsrichtung aufweisen, prallen diese auch auf alle angrenzenden Flächen gleichermaßen. Die bei diesen Kollisionen entstehenden Stoßkräfte, welche letztlich Ursache für den Druck sind, sind somit in alle Richtungen identisch. Physikalisch wird dieser Sachverhalt durch das sogenannte Äquipartitionstheorem (Gleichverteilungssatz) beschrieben. Ausführlichere Informationen zum Druck in Gasen finden sich im Artikel Gasdruck wieder.

Druck von Flüssigkeiten und Gasen auf gekrümmte Oberflächen
Die untere Abbildung zeigt ein unter Druck stehendes Gas (oder auch eine Flüssigkeit) in einem Zylinder, der mit einem beweglichen Kolben verschlossen ist. Die vom Fluid auf den Kolben ausgeübte Kraft lässt sich gemäß der Definition des Druckes als Produkt von Druck p und Kolbenfläche A berechnen:
\begin{align}
\label{a}
&F = p \cdot A \\[5px]
\end{align}
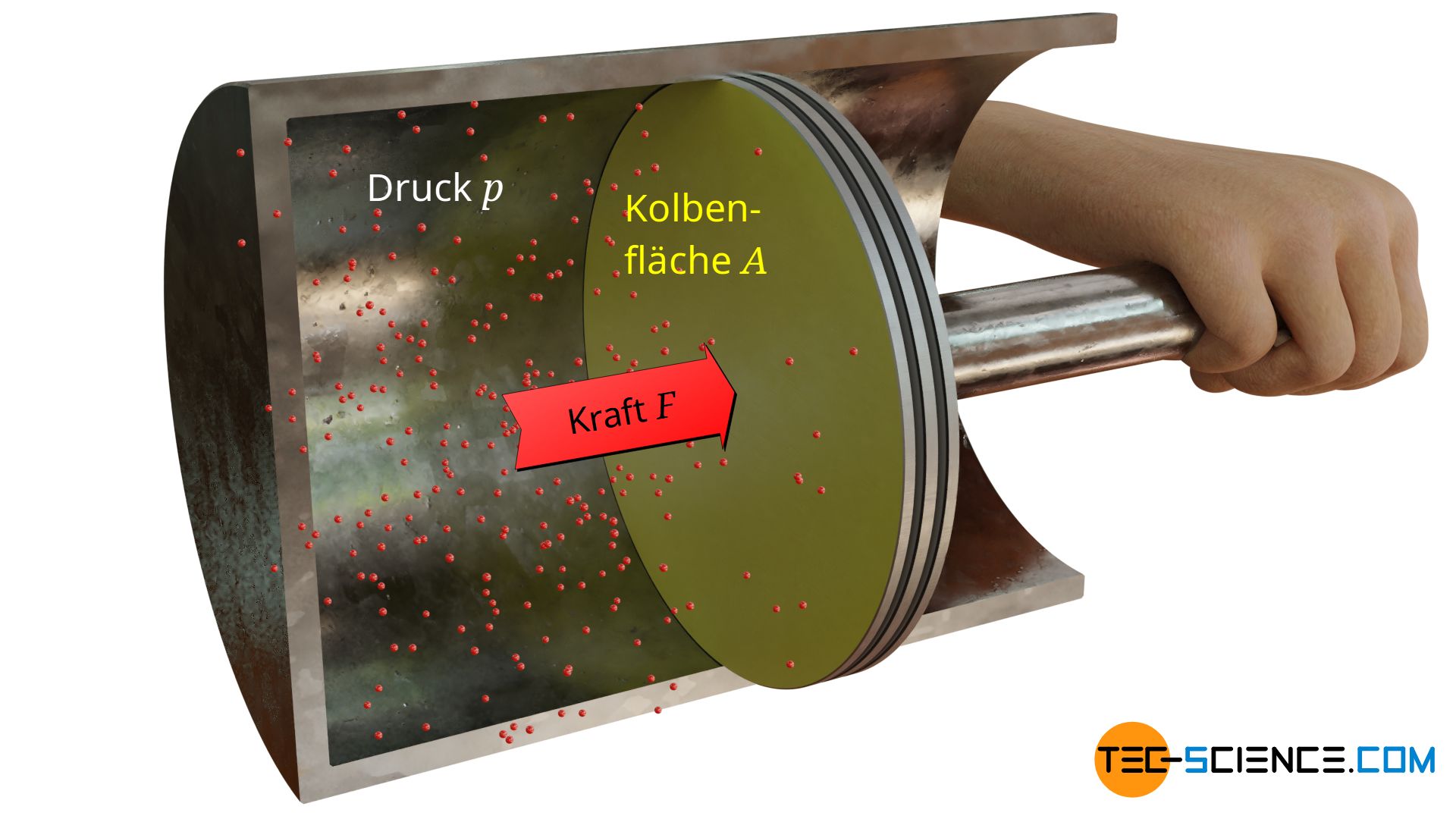
In der bisherigen Betrachtung wurde stets von einer ebenen Fläche ausgegangen, auf die der Druck wirkt und hierdurch eine entsprechende Kraft ausübt. Wie ändert sich aber die Kraftwirkung, wenn es sich nicht mehr um eine flache sondern um eine gekrümmte Oberfläche handelt? Die untere Abbildung zeigt hierzu einen Kolben, dessen Oberfläche nicht mehr eben ist (die Oberfläche auf die der Druck lastet ist zur besseren Sichtbarkeit gelb eingefärbt).
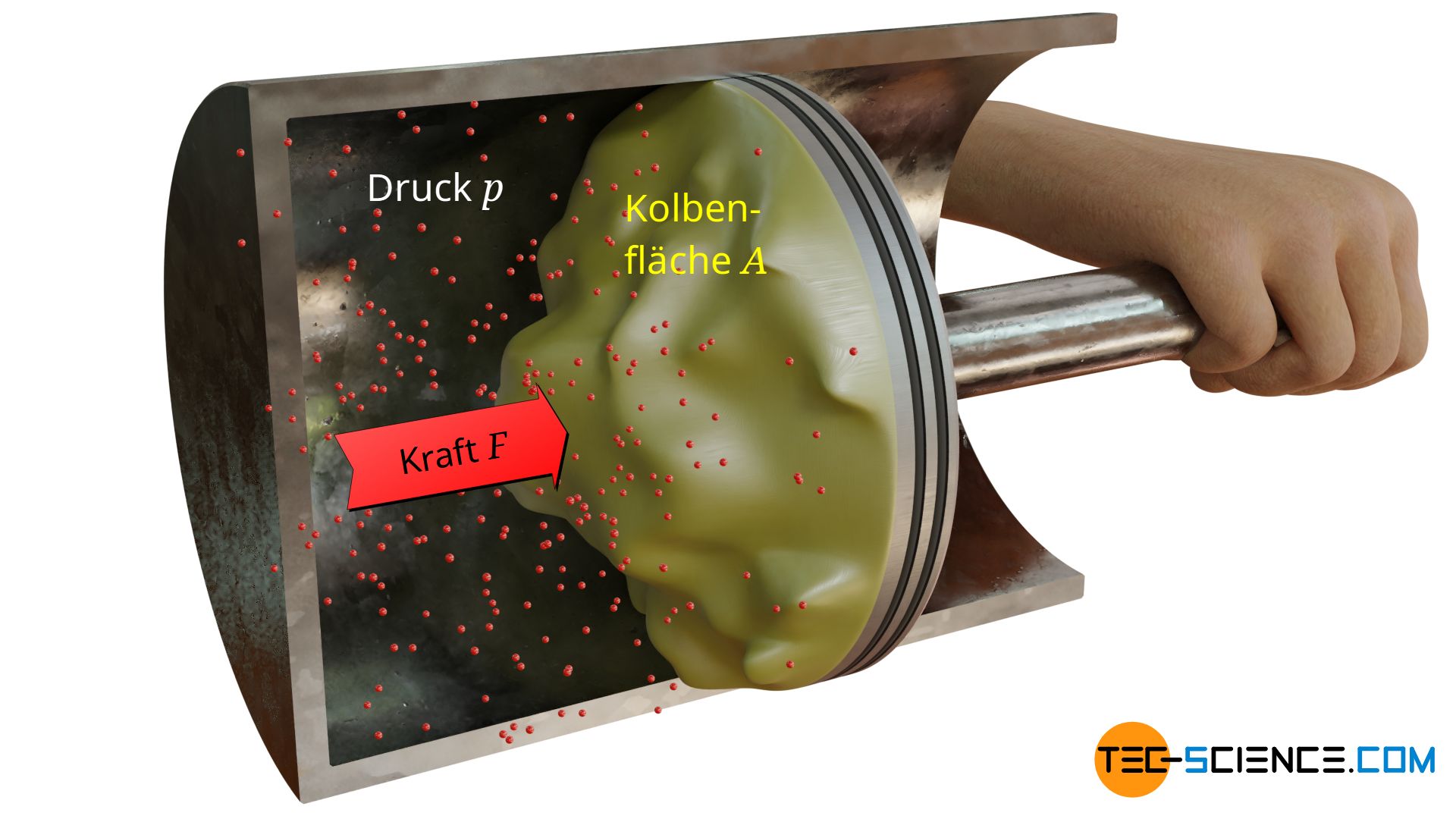
Aufgrund der Krümmungen hat der Kolben nun eine insgesamt größere Oberfläche. Man könnte deshalb vorschnell zu dem Schluss kommen, dass sich durch die vergrößerte Kolbenoberfläche auch die Kraft auf den Kolben gemäß Gleichung (\ref{a}) erhöht. Tatsächlich wird aber die Kraft auf den Kolben jedoch dieselbe sein! Die Form der Oberfläche hat also keinen Einfluss auf die Kraft, die der Druck verursacht.
An einem einfachen Beispiel aus dem Alltag kann man dieses zunächst paradox erscheinende Phänomen relativ einfach demonstrieren. Hierzu hält man den Kolben ohne Zylinder einfach in die Luft. Beide Seiten des Kolbens sind in diesem Fall demselben Luftdruck ausgesetzt. Dieser Luftdruck kommt durch die umgebenden Luftteilchen zustande, die auf beide Seiten des Kolbens prallen. Offensichtlich wird der Kolben dabei aber weder in die eine noch in die andere Richtung gedrückt, sondern bleibt in Ruhe. Da sich der Kolben also im Kräftegleichgewicht befindet, muss die vom Umgebungsdruck auf die ebene Oberfläche ausgeübte Kraft genauso groß sein wie auf die gekrümmte Oberfläche.
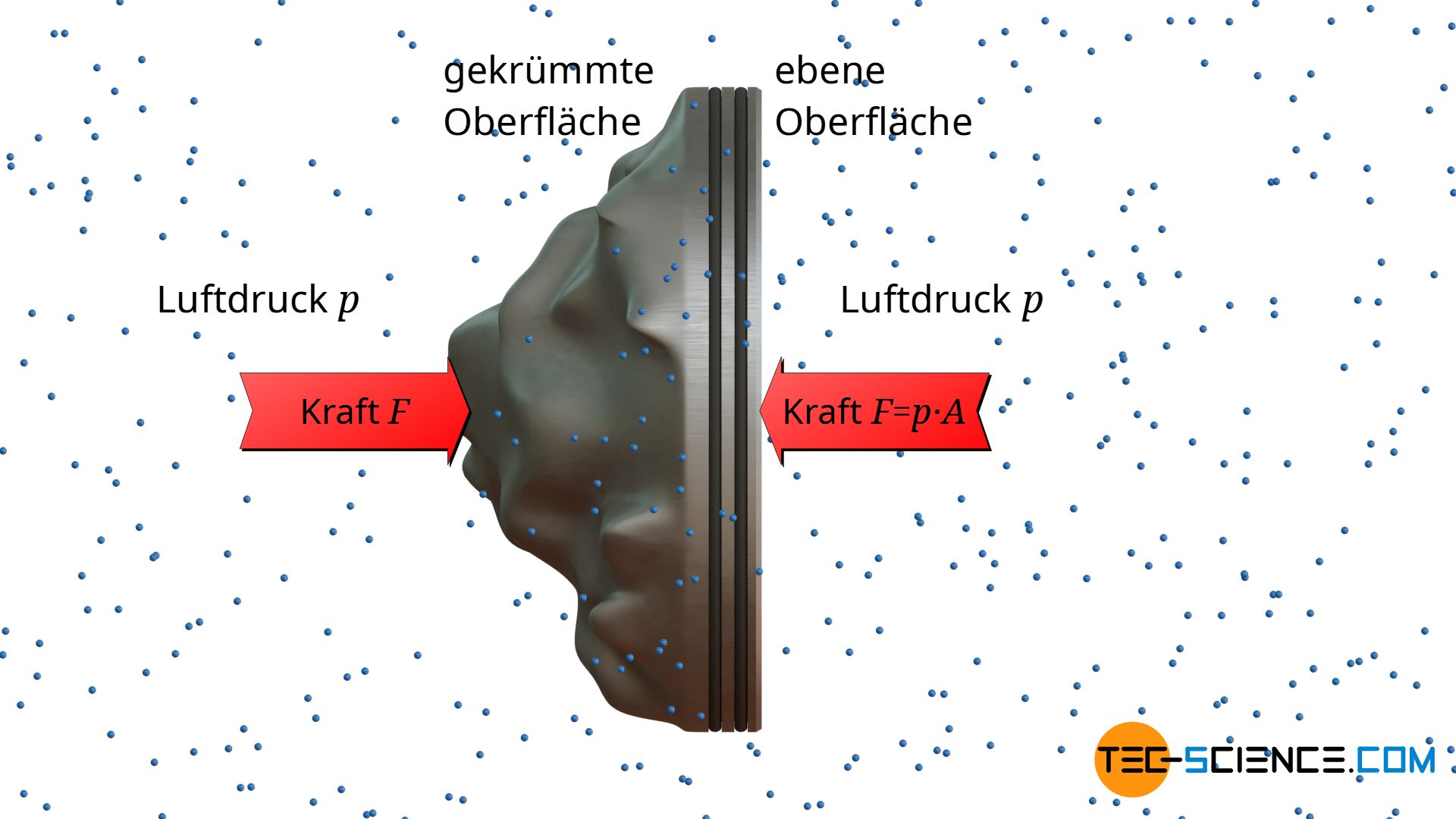
Salopp formuliert ist also zur Berechnung der Kraft auf eine gekrümmte Oberfläche stets die flache Oberfläche zugrunde zu legen; präziser gesagt: die in Kraftrichtung projizierte Fläche. Man kann sich dabei einfach vorstellen, man bestrahlt die gekrümmte Oberfläche in Kraftrichtung mit einer Taschenlampe. Die Fläche des dabei entstehenden Schattens auf einer ebenen Wand, entspricht der in Kraftrichtung projizierten Fläche.

Zur Berechnung der Kraft, den der Druck eines Gases oder einer Flüssigkeit auf eine beliebig gekrümmte Oberfläche ausübt, muss die in Kraftrichtung projizierte Fläche zugrunde gelegt werden!
Man kann sich diese Tatsache auch anschaulich erklären. Hierzu stellt man sich die gekrümmte Oberfläche als aus vielen Treppenstufen aufgebaut vor (was auf atomarere Ebene durch die Atome letztlich ja auch der Fall ist). Nur senkrecht zur Kraftwirkung angeordnete Flächen erzeugen beim Aufprall der Fluidteilchen eine Kraftwirkung in die entsprechende Richtung (gelb markierte Pfeile). Prallen Teilchen auf die seitlichen Flächen so erzeugen diese zwar auch eine Kraft, aber nicht in betrachteter Richtung sondern senkrecht dazu (weiße Pfeile). Somit wird deutlich, dass also nur Flächenanteile relevant sind, die senkrecht zur betrachteten Kraftwirkung angeordnet sind. Dies entspricht gerade der projizierten Fläche!

Kompressibilität & Inkompressibilität
Auch wenn sich Gase und Flüssigkeiten hinsichtlich ihrer räumlichen Druckwirkung sehr ähneln, gibt es aber einen entscheidenden Unterschied. Dieser zeigt sich, wenn man einmal versucht ein Gas und einmal eine Flüssigkeit zu komprimieren, d.h. das Volumen zu verkleinern. Schließt man hierzu Luft in einen Zylinder ein und komprimiert diese mit einem beweglichen Kolben, dann steigt der Gasdruck unter Volumenverkleinerung stark an. Wird anstelle des Gases jedoch eine Flüssigkeit verwendet, dann steigt der Flüssigkeitsdruck zwar ebenfalls stark an, aber (nahezu) ohne Volumenverkleinerung.

Im Gegensatz zu Gasen können Flüssigkeiten also nicht komprimiert werden. Dies gilt auch für viele Festkörper, wie bspw. Metalle. Solche Stoffe, die ihr Volumen unter Druck nicht ändern, werden auch als inkompressibel bezeichnet. Stoffe wie Gase, die ihr Volumen unter Druck hingegen sehr stark ändern, werden kompressibel genannt.
Als inkompressibel werden Stoffe bezeichnet, die ihr Volumen unter Druckeinwirkung nicht ändern!
Beachte, dass sich der Begriff der Inkompressibilität nur auf das Volumen des Stoffes bezieht und nicht auf die Form. Ein Stahlwürfel wird zwar unter dem hohen Druck einer Presse die Form ändern, nicht aber das Volumen. Das Volumen ist durch die Stoffdichte und die Masse fest vorgegeben. Da die Stoffdichte ϱ eine Materialkonstante ist und die Masse m sich bei der Umformung nicht ändert, bleibt folglich auch das Volumen V konstant (V=m/ϱ). Stahl ist also trotz der änderbaren Form inkompressibel! Dies gilt auch für Flüssigkeiten, die zwar ihre Form, nicht aber ihr Volumen ändern können können.






