Die Wärmeleitfähigkeit ist ein Maß wie gut oder schlecht ein Material Energie in Form von Wärme durch sich hindurch leitet (Maß für die Stärke der Wärmeleitung)!
Wärmeleitung
Im Allgemeinen kann Wärme auf drei unterschiedliche Arten übertragen werden (zu den nachfolgend genannten Arten finden sich im Artikel Wärmeübertragung mehr Informationen):
- durch Wärmeströmung,
- Wärmestrahlung und
- Wärmeleitung.
Vor allem in Festkörpern hat die Wärmeleitung große technische Bedeutung, aber auch in dünnen Gasen bei erhöhten Temperaturen überwiegt die Wärmeleitung gegenüber der Wärmestrahlung und Konvektion. So sollten bspw. Häuserwände oder mit Luft aufgeschäumte Dämmplatten nur in geringem Maße Wärme hindurchleiten. Dies stellt sicher, dass im Winter nur wenig Energie durch Wärme von innen nach außen dringt. Dadurch verhindert man, dass die Wohnung zu schnell auskühlt. Gleichzeitig hat dies den Vorteil, dass bei geringer Wärmeleitung Wärme im Sommer nur in geringem Maße von außen in die Wohnung dringt. Auf diese Weise bleibt die Wohnung angenehm kühl.

Aufgrund der besonderen Bedeutung der Wärmeleitung soll diese deshalb im Folgenden näher charakterisiert werden. Dabei zeigt bereits die Alltagserfahrung zeigt, dass verschiedene Materialien unterschiedliche gut Wärme leiten. Metalle sind im allgemeinen sehr gute Wärmeleiter, wohingegen Plastik oder Holz die Wärme meist nur in geringerem Maße leiten. Aus diesem Grund sind Griffe an heißen Metallgegenständen wie Ofentüren bspw. aus Holz (siehe hierzu auch den Artikel Menschliches Wärmeempfinden). Aus demselben Grund findet man auch an Wasserkocher aus Metall meist einen Griff aus Plastik.

Unabhängig des Materials stellt sich zunächst die Frage, welche Größen sonst Einfluss darauf haben wie viel Wärme ein Material durch sich hindurch leitet.
Einfluss der Temperaturdifferenz
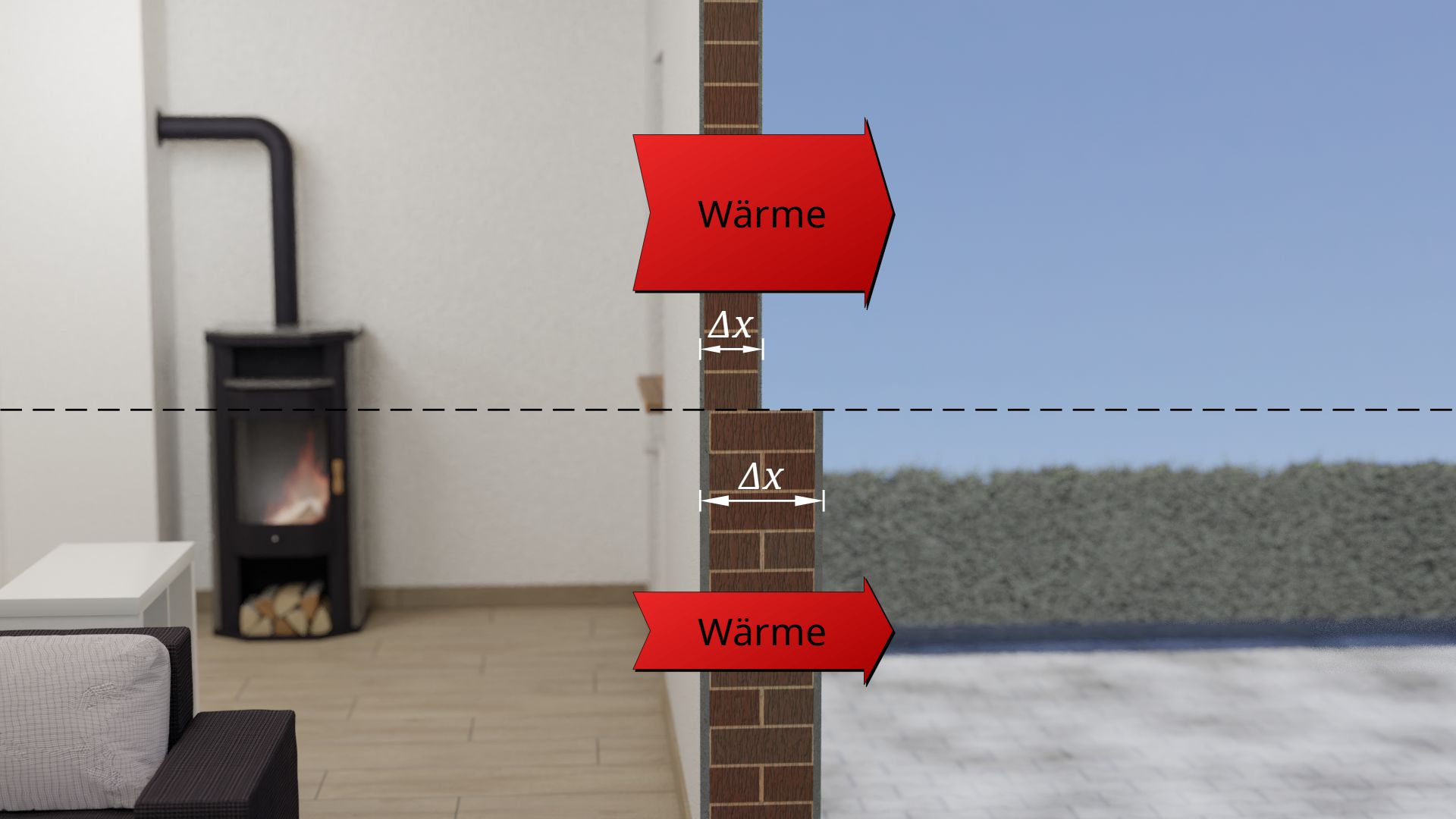
Damit ein Wärmestrom überhaupt entstehen kann, muss zunächst zwingend eine Temperaturdifferenz am betrachteten Gegenstand vorhanden sein. Um beim Beispiel der Hauswand zu bleiben, ist der Grund für den Wärmestrom die Temperaturdifferenz zwischen dem Inneren des Hauses und der freien Umgebung.

Die Praxis zeigt dabei, dass umso mehr Wärme durch die Hauswand strömt, je größer die Temperaturdifferenz ist. Dies ist auch der Grund weshalb im Winter mehr geheizt werden muss als im Herbst oder Frühling. Durch die größere Temperaturdifferenz im Winter zwischen Innenseite und Außenseite der Wand, ist der hindurchgehende Wärmestrom größer als im Frühling, wenn die Temperaturdifferenz geringer ist. Ist die Temperaturdifferenz null, d.h. die Außenluft hat dieselbe Temperatur wie die Luft im Haus, dann muss sogar gar nicht geheizt werden. Demzufolge dringt auch keine Wärme durch die Wand nach außen.
Der Wärmestrom durch einen wärmeleitenden Gegenstand ist umso größer, je größer die Temperaturdifferenz von der einen zur anderen Seite des Gegenstandes ist!
Genauere Untersuchungen zeigen, dass der Wärmestrom Q* durch einen Gegenstand nahezu proportional zur vorhandenen Temperaturdifferenz ΔT ist. Eine Vervielfachung der Temperaturdifferenz bedeutet demnach einen im selben Maße erhöhten Wärmestrom:
\begin{align}
&\dot Q \sim \Delta T \\[5px]
\end{align}
Einfluss der Dicke des Materials
Des Weiteren beeinflusst die Dicke des Gegenstandes den Wärmestrom. Auch dabei zeigt bereits die Alltagserfahrung, dass der hindurchgehende Wärmestrom durch einen Gegenstand umso größer ist, je dünner der Gegenstand ist. Umgekehrt bedeutet dies natürlich, dass der Wärmestrom umso geringer ist, je dicker das Material ist. Deshalb zieht man im Winter schließlich auch eine dicke Jacke an anstelle einer dünnen.
Auch bei Gebäudewänden zeigt sich deutlich der Einfluss der Materialdicke auf den Wärmestrom. Dicke Wände lassen das Gebäude weniger schnell auskühlen als relativ dünne Gebäudewände. Der Wärmestrom durch eine dicke Wand ist offensichtlich geringer als durch eine dünne.
Heizkörper in älteren Gebäuden, die aus optischen Gründen etwas in die Gebäudewände eingelassen sind (sog. Heizkörpernischen), sind aus energetischen Gründen deshalb in zweierlei Hinsicht sehr ungünstig. Zum einen ist dort die Gebäudewand relativ dünn, was ohnehin schon einen großen Wärmestrom verursacht. Zum anderen befindet sich dort auch noch die Heizung, d.h. es herrscht an der Innenwand eine sehr hohe Temperatur. Die Temperaturdifferenz zwischen innen und außen ist somit ebenfalls relativ hoch, was den abgehend Wärmestrom nochmals vergrößert! Das Anbringen von Reflexionsfolie hinter dem Heizkörper bringt (anders als viele Hersteller behaupten) so gut wie keinen wahrnehmbaren Dämmeffekt. Reflektierende Folie hilft nur gegen Wärmestrahlung, nicht aber gegen den weitaus größeren Effekt der Wärmeleitung!

Der Wärmestrom durch einen wärmeleitenden Gegenstand ist umso geringer, je dicker das Material ist!
Genauere Untersuchungen zeigen, dass eine Verdopplung der Materialdicke eine Halbierung des Wärmestroms bedeutet. Wärmestrom Q* und Materialdicke Δx stehe also in einem umgekehrt proportionalen Verhalten:
\begin{align}
&\dot Q \sim \frac{1}{\Delta x} \\[5px]
\end{align}
Einfluss der Fläche des Materials
Der Wärmestrom ist auch direkt von der Fläche abhängig durch den der Wärmestrom tritt, d.h. die Querschnittsfläche senkrecht zum Wärmestrom. Im Fall einer Gebäudewand entspricht dies der Fläche der Wand. Umso größer die Fläche, desto mehr Wärme kann durch die Fläche bzw. durch den Gegenstand dringen. Folglich ist der Wärmestrom bei großen Flächen auch relativ hoch. Deshalb sind die Heizkosten bei Gebäuden mit vielen großen Fenstern (die die Wärme im Vergleich zu den Gebäudewänden meist besser leiten) im Allgemeinen höher als bei Gebäuden mit nur wenigen kleinen Fenstern. Durch die große Fensterfläche dringt viel Wärme nach außen, d.h. der hindurchgehende Wärmestrom ist relativ hoch.
Der Wärmestrom durch einen wärmeleitenden Gegenstand ist umso größer, je größer die Querschnittsfläche des Materials ist!
Die Verringerung eines Wärmestroms durch eine entsprechende Verkleinerung der Fläche, zeigt sich unbewusst auch bei uns Menschen. Das Zusammenkauern des Körpers bei Kälte ist genau ein solches instinktives Verhalten, das auf dem Prinzip der Verkleinerung der Fläche beruht. Von allen geometrischen Formen hat die Kugel nämlich die kleinst mögliche Oberfläche im Verhältnis zum Volumen und ist somit energetisch betrachtet extrem günstig. Mit dem Zusammenkauern versucht man letztlich die Form einer Kugel anzunehmen. Damit ist man versucht eine möglichst geringe Fläche zu erzeugen die in Kontakt mit der kalten Umgebung steht. Auf diese Weise erzielt man einen geringen abgehenden Wärmestrom und der Körper bleibt länger warm.

Genauere Untersuchungen zeigen, dass der Wärmestrom proportional zur Fläche ist. Dies kann man auch anschaulich sehr leicht nachvollziehen. Hierzu kann man sich bspw. zwei identische Flächen an einer Gebäudewand vorstellen. Durch beide Flächen tritt derselbe Wärmestrom. Nun nimmt man in Gedanken beide Flächen zu einer großen zusammen, d.h. man verdoppelt die Fläche. Offensichtlich fließt dann auch insgesamt der doppelte Wärmestrom durch die doppelt so große Fläche hindurch. Wärmestrom und Fläche sind also proportional zueinander:
\begin{align}
&\dot Q \sim A \\[5px]
\end{align}

Die verstärke Wärmeleitung durch größere Oberflächen macht man sich bspw. bei Heizkörpern zunutze. Heizkörper werden aus diesem Grund meist nicht aus einem Stück gebaut, sondern bestehen aus vielen Rippen. Dies vergrößert die Fläche, was zu einem insgesamt größeren Wärmestrom führt. Die Wohnung wird schneller warm.

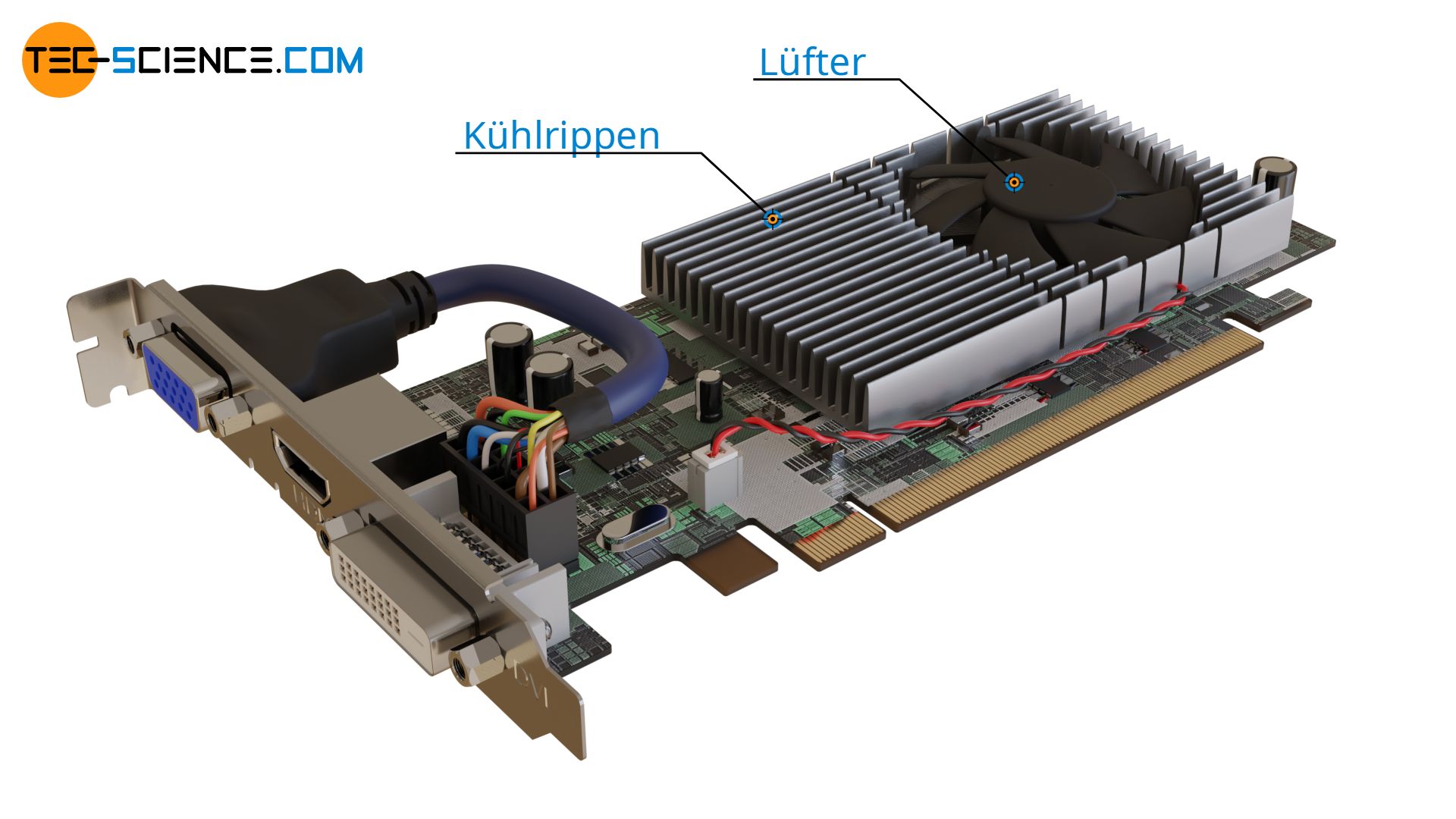
Die Funktionsweise von Kühlrippen beruht im Prinzip ebenfalls auf der Vergrößerung der Fläche und dem entsprechend höheren Wärmestrom. Nur, dass in diesem Fall Wärme nicht zugeführt, sondern abgeführt wird. Hierdurch kann der Gegenstand schneller gekühlt werden. Die untere Abbildung zeigt hierzu die Anwendung von Kühlrippen zur Kühlung des Chips (GPU) einer Grafikkarte.
Fouriersches Gesetz
Wie die oben beschriebenen Zusammenhänge zeigen, ist der Wärmestrom Q* durch ein Material also proportional zur Temperaturdifferenz ΔT und proportional zur Fläche des Materials A, sowie umgekehrt proportional zu dessen Dicke Δx. Dies lässt sich wie folgt darstellen:
\begin{align}
\dot Q &\sim \frac{\Delta T \cdot A }{\Delta x}\\[5px]
\end{align}
Diese Gesetzmäßigkeit gilt zunächst unabhängig des Materials, d.h. bei jedem Material wird der Wärmestrom proportional zu Temperaturdifferenz und zur Fläche sowie umgekehrt zur Dicke sein. Durch Einführung einer materialabhängigen Proportionalkonstanten λ kann diese Gesetzmäßigkeit aber schließlich als Gleichung formuliert werden. Dieser Zusammenhang wird auch als Fouriersches Gesetz bezeichnet.
\begin{align}
\label{q}
&\boxed{\dot Q =\lambda \cdot \frac{\Delta T \cdot A }{\Delta x}} ~~~~~\text{mit}~~~~~[\lambda]=\frac{\text{W}}{\text{m} \cdot \text{K}} ~~~~~\text{Wärmeleitfähigkeit}\\[5px]
\end{align}
Das Fouriersche Gesetz beschreibt den Wärmestrom der durch Wärmeleitung durch ein Material tritt!
Der Proportionalitätsfaktor λ in der oberen Gleichung wird Wärmeleitfähigkeit, thermische Leitfähigkeit oder Wärmeleitkoeffizient genannt und ist maßgeblich durch das Material des Gegenstandes bestimmt. Die Wärmeleitfähigkeit hat die Einheit W/(m·K) („Watt pro Meter und Kelvin“). Eine Wärmeleitfähigkeit von bspw. 2,4 W/(m·K) bedeutet anschaulich, dass bei einer Materialdicke von einem Meter, ein Wärmestrom von 2,4 Watt (d.h. 2,4 Joule pro Sekunde) durch eine Fläche von einem Quadratmeter tritt, wenn die Temperaturdifferenz ein Kelvin beträgt.
Die Wärmeleitfähigkeit ist ein Maß wie gut oder schlecht ein Material Energie in Form Wärme durch sich hindurch leitet („Maß für die Stärke der Wärmeleitung“)! Sie gilt nur für die Wärmeübertragung durch Wärmeleitung, nicht durch Konvektion oder Strahlung!
Das Fouriersche Gesetz gilt in dieser Form nur, wenn die Flächen durch die der Wärmestrom tritt eben und parallel zueinander sind. Tatsächlich ist die Wärmeleitfähigkeit aber keine reine Stoffkonstante, sondern von der Temperatur abhängig. Bei großen Temperaturdifferenzen kann sich deshalb die Wärmeleitfähigkeit über die Dicke des Materials hinweg relativ stark ändern. In diesen Fällen ist mit einem mittleren Wärmeleitkoeffizienten zu rechnen.
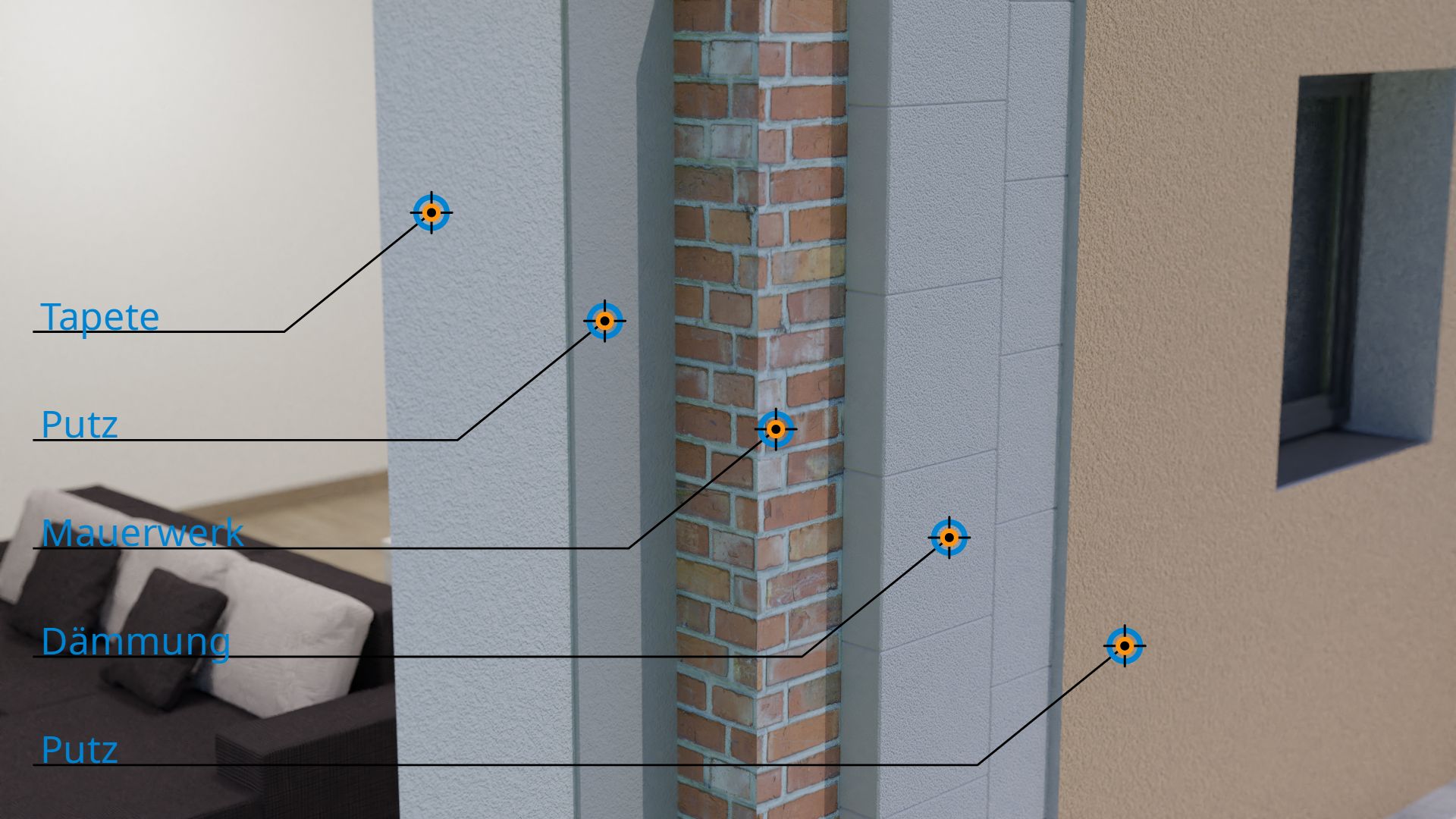
Ferner gilt zu beachten, dass der Wärmeleitkoeffizient nur den Wärmetransport durch Wärmeleitung im inneren eines Materials beschreibt. Nicht berücksichtigt sind Wärmetransportvorgänge an der Grenzschicht durch Konvektion. Zudem hat man es beim Wärmetransport durch eine Hauswand im Allgemeinen mehrere Schichten, die den Wärmedurchgang beeinflussen. Von innen nach außen könnten dies bspw. sein: Tapete → Putz → Mauerwerk → Dämmung → Putz. Solche Wärmedurchgänge durch Materialien und deren Grenzschichten werden im Artikel Wärmedurchgangskoeffizient (U-Wert) näher betrachtet.
Informationen zur experimentellen Bestimmung der Wärmeleitfähigkeit finden sie im verlinkten Artikel.
Wärmestromdichte & Temperaturgradient
Gleichung (\ref{q}) beschreibt den Wärmestrom in Abhängigkeit von geometrischen Größen des Materials wie Fläche und Dicke. Durch Umstellen dieser Gleichung lassen sich diese geometrischen Abhängigkeiten jedoch leicht beseitigen:
\begin{align}
\dot Q &= \lambda \cdot \frac{ \Delta T }{\Delta x} \cdot A \\[5px]
\label{u}
\underbrace{\frac{\dot Q}{A}}_{\text{Wärmestromdichte } \dot{q}} &=\lambda \cdot \underbrace{\frac{\Delta T}{\Delta x}}_{\text{Temperaturgradient }\nabla{T}} \\[5px]
\end{align}
Der Quotient auf der linken Seite, bestehend aus Wärmestrom und Fläche, beschreibt den pro Flächeneinheit hindurchtretenden Wärmestrom. Er lässt sich somit als Wärmestromdichte q* interpretieren.
Als Wärmestromdichte bezeichnet man den pro Flächeneinheit durchtretenden Wärmestrom!
Auch der Quotient auf der rechten Seite aus Temperaturdifferenz und Materialdicke lässt sich anschaulich interpretieren. Dieser Quotient beschreibt letztlich den Abfall der Temperatur pro Längeneinheit, d.h. ein sogenanntes Temperaturgefälle. Eine solche räumliche Änderung einer Größe entlang einer Strecke wird allgemein auch als Gradient bezeichnet. In diesem Fall wird das Temperaturgefälle also auch als Temperaturgradient ∇T bezeichnet. Der Temperaturgradient entspricht der Steigung des Temperaturprofils. Symbolisiert wird ein Gradient meist durch ein umgekehrtes Delta-Zeichen (auch Nabla-Operator genannt).
Als Temperaturgradient bezeichnet man die Temperaturänderung pro Längeneinheit („Temperaturgefälle“)!
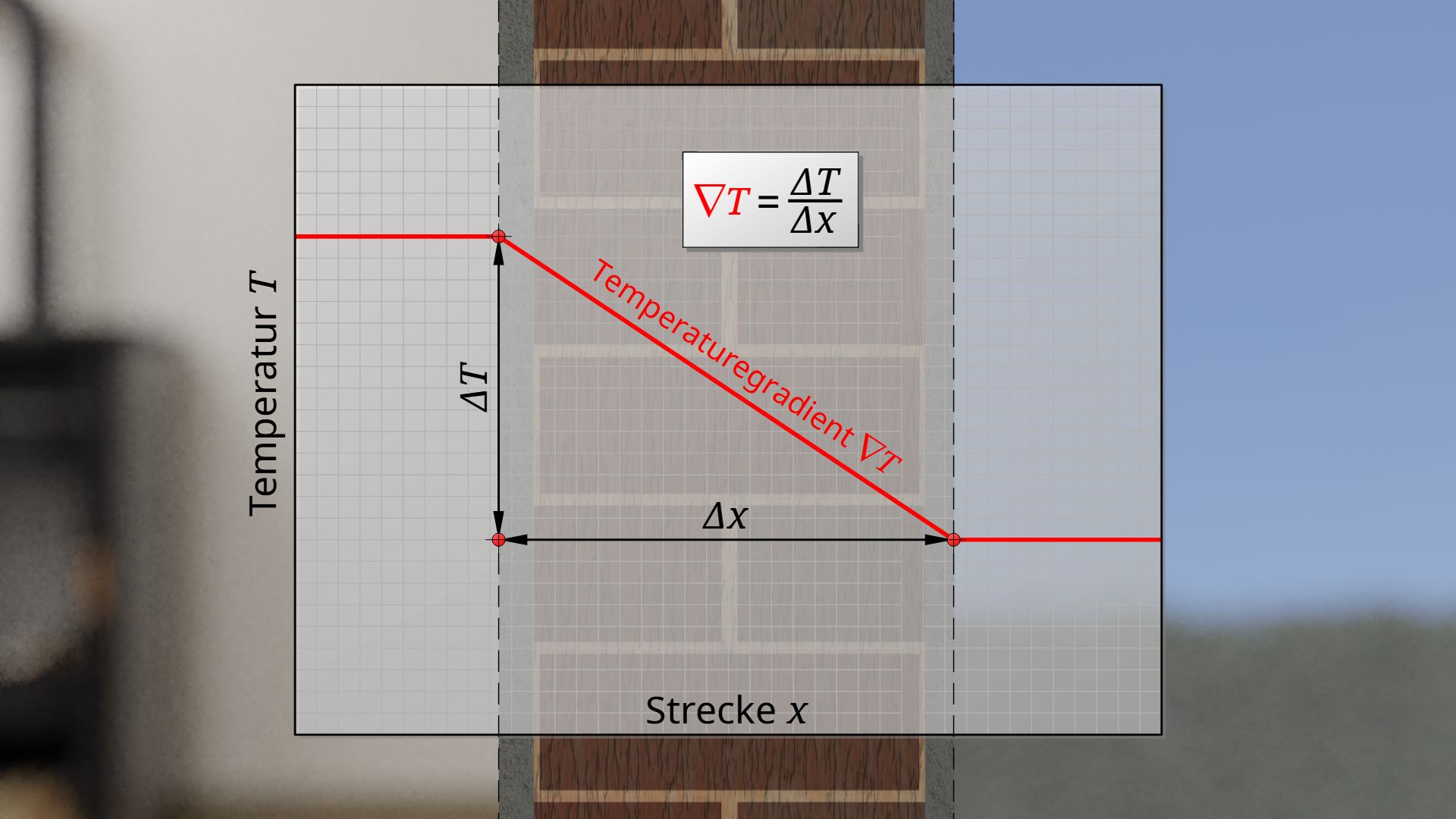
Für eine korrekte mathematische Beschreibung muss in Gleichung (\ref{u}) (und eigentlich auch in Gleichung (\ref{q})) zusätzlich noch ein Minuszeichen eingeführt werden, da der Wärmestrom stets in Richtung abnehmender Temperatur fleißt. Der Wärmestrom fließt salopp formuliert von warm nach kalt, d.h. in Richtung negativem Temperaturgradienten.
\begin{align}
\label{r}
&\boxed{\dot{q} = -\lambda \cdot \nabla{T}}
\end{align}
Die Wärmeleitfähigkeit eines Materials beschreibt vor diesem Hintergrund also den Zusammenhang zwischen einem vorhandenem Temperaturgradienten und der hieraus resultierenden Wärmestromdichte. Die als Beispiel bereits erwähnte Wärmeleitfähigkeit von 2,4 W/(m·K) kann demnach auch wie folgt interpretiert werden: Bei einem Temperaturgradienten von 1 K/m tritt durch das betrachtete Material eine Wärmestromdichte von 2,4 W/m². Bei dieser Interpretation spielt weder die Fläche, noch die Dicke des Materials eine Rolle spielt. Diese Größen sind in der Wärmestromdichte bzw. im Temperaturgradienten sozusagen bereits „inbegriffen“. Obere Gleichung ist somit unabhängig von geometrischen Materialwerten!
Auch die in diesem Zusammenhang häufig gehörte Aussage, dass das Fourier’sche Gesetz nur für eindimensionale Wärmeströme mit ebenen, parallelen Flächen gilt, ist in diesem Zusammenhang irrelevant. Eine solche Einschränkung trifft nur auf die Gleichung (\ref{q}) zu, die den Wärmestrom im makroskopischen Maßstab beschreibt, nicht aber für Gleichung (\ref{r})! Gleichung (\ref{r}) macht eine Aussage über die Wärmestromdichte in einem einzigen Punkt eines Materials in Abhängigkeit des dort vorhandenen Temperaturgradienten. Irgendwelche Fläche haben in einem solchen Punkt überhaupt keine Relevanz. Gleichung (\ref{r}) bildet die Grundlage für die Wärmeleitungsgleichung, mit der auch dreidimensionale Wärmeleitungsvorgänge in beliebig geformten Körpern, mit nicht-parallelen Flächen beschrieben werden.
Wärmeleitfähigkeit ausgewählter Materialien
Die unteren Tabellen zeigen eine Auswahl an verschiedenen Materialien mit zugehörender Wärmeleitfähigkeit (Quelle: Wikipedia und energie-lexikon). Die angegebenen Werte beziehen sich dabei auf eine Temperatur von 20 °C. Es ist zu erkennen, dass Festkörper und insbesondere Metalle relativ hohe Wärmeleitfähigkeiten aufweisen, wohingegen Kunststoffe meiste geringere Koeffizienten haben. Nochmals geringere Werte finden sich im Allgemeinen bei Flüssigkeiten wieder, die nur noch von Gasen unterboten werden. Die Unterschiede kommen maßgeblich durch den charakteristischen atomaren Aufbau zustande. Mehr dazu im Artikel Wärmeleitung.
Die Wärmeleitfähigkeit nimmt im Allgemeinen ausgehend von Metallen, über Kunststoffe und Flüssigkeiten, bis hin zu Gasen ab!
Auffällig bei Metallen ist die relativ hohe Wärmeleitfähigkeit von Kupfer. Deshalb nutzt man Kupfer auch bspw. als Material zum Bau von Kühlelementen wie PC-Kühler. Wärme kann hierdurch sehr schnell von der Wärmequelle abgeführt werden. Silber hätte zwar eine noch höhere thermische Leitfähigkeit, ist jedoch deutlich teurer.
| Metalle | Wärmeleitfähigkeit in W/(m·K) bei 20°C |
| Silber | 429 |
| Kupfer | 401 |
| Gold | 314 |
| Aluminium | 236 |
| Wolfram | 170 |
| Magnesium | 156 |
| Messing | 120 |
| Zink | 110 |
| Nickel | 85 |
| Eisen | 80 |
| Platin | 71 |
| Stahl | ~50 |
| Blei | 35 |
| Titan | 22 |
| Weitere Feststoffe | Wärmeleitfähigkeit in W/(m·K) bei 20°C |
| Graphen | 5300 |
| Diamant | 2300 |
| Aluminiumnitrid | ~200 |
| Silicium | 148 |
| Korund | 42 |
| Aluminiumoxid | 28 |
| Eis (-10°C) | 2,3 |
| Beton | 2,0 |
| Kreide | 1 |
| Kalksandstein | ~1 |
| Porenbeton (Gasbeton) | 0,2 |
| Holz | ~0,15 |
| Kunststoffe | Wärmeleitfähigkeit in W/(m·K) bei 20°C |
| Polyethylen | ~ 0,45 |
| Polytetrafluorethylen („Teflon“) | 0,25 |
| Polyurethan (nicht geschäumt) | 0,25 |
| Polypropylen | 0,23 |
| Epoxidharz (EP) | 0,20 |
| Polymethylmethacrylat (Plexiglas) | 0,19 |
| Polyvinylchlorid (PVC) | 0,17 |
| Polysterol (nicht geschäumt) | 0,17 |
| Flüssigkeiten | Wärmeleitfähigkeit in W/(m·K) bei 20°C |
| Wasser | 0,60 |
| Schwefelsäure | 0,54 |
| Alkohol | 0,17 |
| Benzin | 0,14 |
| Öl | 0,14 |
| Gase | Wärmeleitfähigkeit in W/(m·K) bei 20°C |
| Wasserstoff | 0,186 |
| Helium | 0,157 |
| Methan | 0,034 |
| Sauerstoff | 0,026 |
| Luft | 0,026 |
| Stickstoff | 0,026 |
| Wasserdampf | 0,025 |
| Argon | 0,018 |
| Kohlenstoffdioxid (CO2) | 0,017 |
| Krypton | 0,010 |
| Xenon | 0,006 |
| Dämmstoffe | Wärmeleitfähigkeit in W/(m·K) bei 20°C |
| Holzfaserplatten | ~0,05 |
| Glaswolle | ~0,04 |
| Zellulose | ~0,04 |
| Wolle | 0,035 |
| Kork | ~0,04 |
| Geschäumtes Polysterol | ~0,04 |