Erfahre in diesem Artikel mehr über die Unterschiede und Bedeutung von Wärmeleitfähigkeit, Temperaturleitfähigkeit, Wärmeübergangskoeffizient und Wärmedurchgangskoeffizient, etc.
Wärmeleitfähigkeit
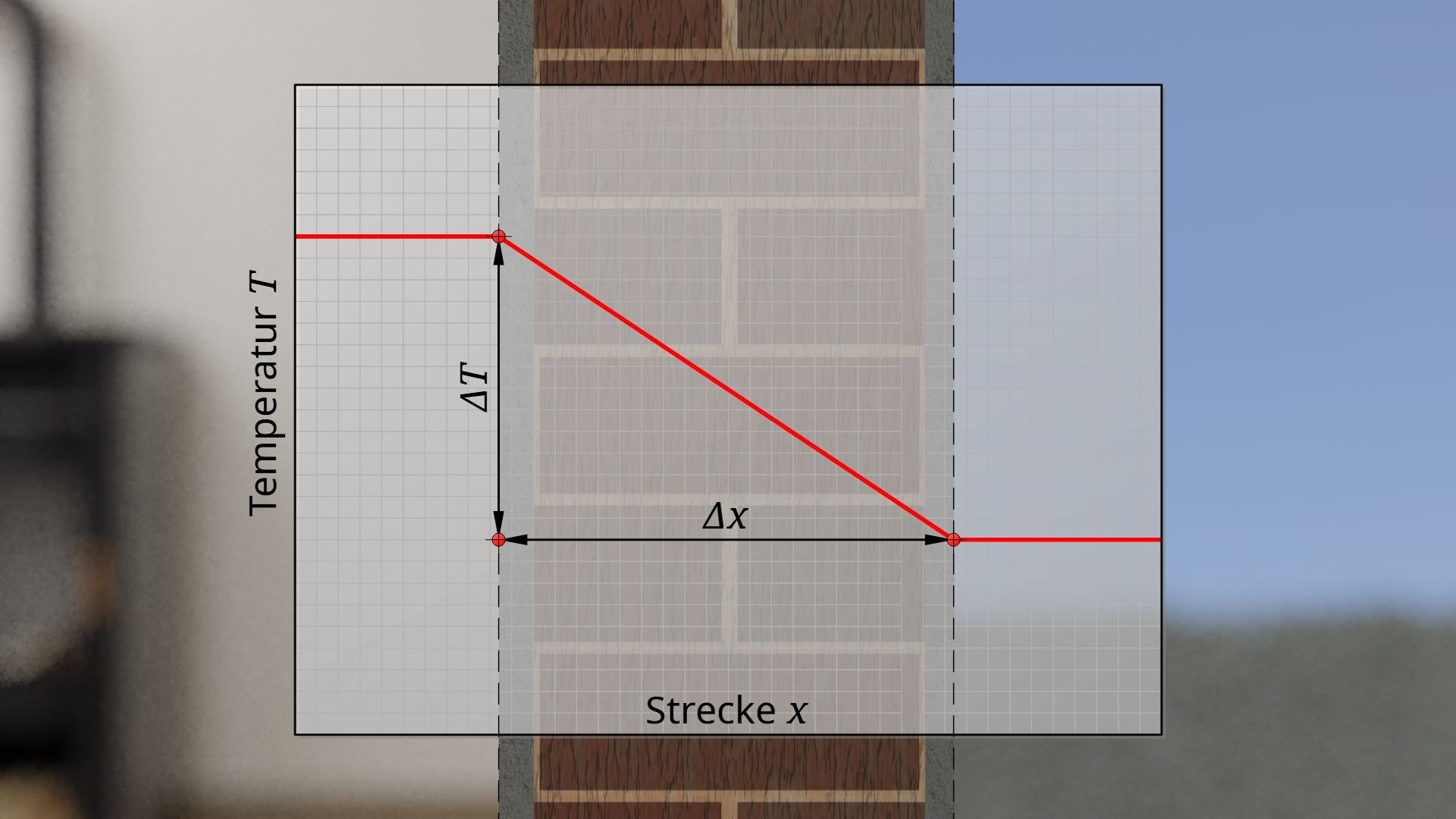
Die Wärmeleitfähigkeit \(\lambda\) beschreibt den stationären Wärmetransport durch Wärmeleitung infolge eines Temperaturgradienten \(\frac{\Delta T}{\Delta x}\). Für den Betrag der Wärmestromdichte \(\dot q\) (= Wärmeleistung pro Flächeneinheit) gilt das Fourier’sche Gesetz:
\begin{align}
&\boxed{\dot q= \lambda \cdot \frac{\Delta T}{\Delta x}}~~~~~\text{Fourier’sches Gesetz} \\[5px]
\end{align}
Mehr Informationen zur Wärmeleitfähigkeit finden sich im Artikel Wärmeleitfähigkeit (Fouriersche Gesetz).
Wärmedurchlasskoeffizient und Wärmedurchlasswiderstand
Bezieht man die Wärmeleitfähigkeit \(\lambda\) auf die Dicke des Gegenstandes \(\Delta x\), durch das die Wärme geleitet wird, so erhält man den Wärmedurchlasskoeffizienten \(\Lambda\) (auch als Wärmedurchlasszahl bezeichnet):
\begin{align}
&\dot q= \underbrace{\frac{\lambda}{\Delta x}}_{\text{Wärmedurchlass-}\\{\text{koeffizient }\Lambda}} \cdot \Delta T \\[5px]
\end{align}
Das Fourier’sche Gesetz lautet in diesem Fall:
\begin{align}
&\boxed{\dot q= \Lambda \cdot \Delta T}~~~\text{mit}~~ \boxed{\Lambda=\frac{\lambda}{\Delta x}}~~\text{als Wärmedurchlasskoeffizient} \\[5px]
\end{align}
Während die Wärmeleitfähigkeit eine charakteristische Stoffgröße ist, die lediglich vom Material abhängig ist, ist der Wärmedurchlasskoeffizient eine bauteilabhängige Größe, da dieser die tatsächliche Dimension des Gegenstandes (Dicke) mitberücksichtigt!
Der Kehrwert des Wärmedurchlasskoeffizienten wird als Wärmedurchlasswiderstand \(R\) bezeichnet:
\begin{align}
&R:=\frac{1}{\Lambda} \\[5px]
&\boxed{R=\frac{\Delta x}{\lambda}} ~~~\text{Wärmedurchlasswiderstand} \\[5px]
\end{align}
Der Wärmedurchlasswiderstand beschreibt als bauteilabhängige Größe die Dämmwirkung eines Bauteils bezüglich der Wärmeleitung (Widerstand gegenüber Wärmeleitung)!
Temperaturleitfähigkeit
Mit der Wärmeleitfähigkeit verknüpft ist die Temperaturleitfähigkeit \(a\) (auch Temperaturleitkoeffizient genannt). Die Temperaturleitfähigkeit ermittelt sich anhand der Dichte \(\rho\) und der spezifischen Wärmekapazität des Stoffes \(c\):
\begin{align}
&\boxed{a=\frac{\lambda}{\rho \cdot c}} ~~~~~\text{Temperaturleitfähigkeit}\\[5px]
\end{align}
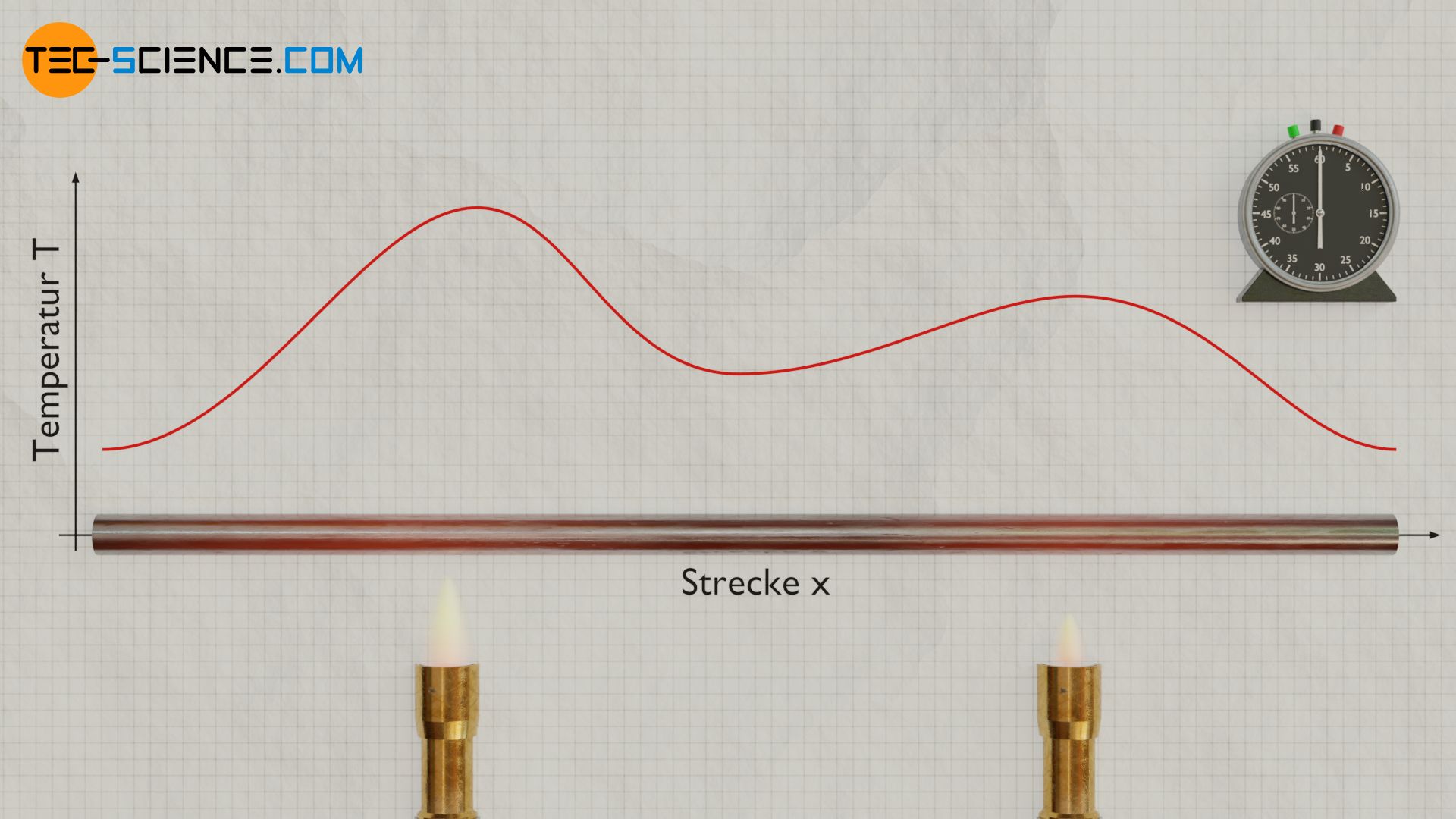
Im Gegensatz zur Wärmeleitfähigkeit beschreibt die Temperaturleitfähigkeit das instationäre Verhalten eines Temperaturfeldes, d.h. die zeitliche Ausbreitung der Temperatur infolge der Wärmeleitung in einem Gegenstand.
Die Temperaturleitfähigkeit \(a\) verknüpft die örtliche Änderung des Temperaturgradienten \(\frac{\partial^2 T}{\partial x^2}\) in einem Punkt mit der hieraus resultierenden zeitlichen Änderung der Temperatur \(\frac{\partial T}{\partial t}\) in diesem Punkt. Der mathematische Zusammenhang wird als Wärmeleitungsgleichung bezeichnet:
\begin{align}
& \boxed{\frac{\partial T}{\partial t} = a \cdot \frac{\partial^2 T}{\partial x^2}}~~~\text{eindimensionale Wärmeleitungsgleichung} \\[5px]
\end{align}
Mit Hilfe der Wärmeleitungsgleichung kann bspw. die zeitliche Temperaturausbreitung entlang eines Stabes ermittelt werden.
Wärmeübergangskoeffizient und Wärmeübergangswiderstand
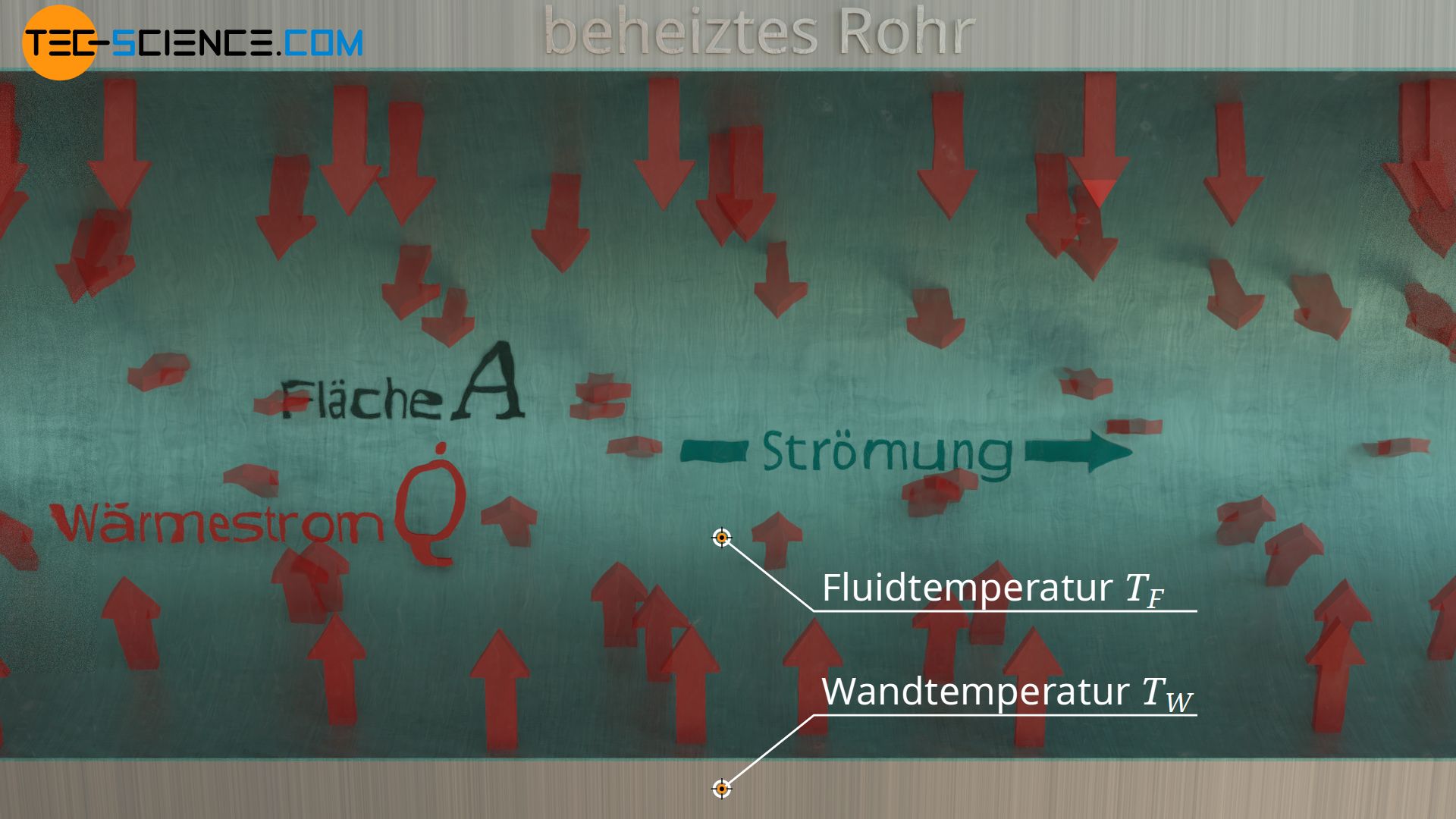
Der Wärmeübergangskoeffizient \(\alpha\) (auch Wärmeübergangszahl genannt) beschreibt den Wärmetransport durch Wärmeströmung (Konvektion) zwischen einem Fluid (Gas oder Flüssigkeit) und einem Feststoff infolge eines Temperaturunterschieds zwischen diesen Medien. Große Bedeutung hat ein solcher Wärmetransport bspw. bei einer Rohrströmung mit Wasser. Zwischen Wasser und Rohrwand wird dabei Wärme durch Konvektion übertragen, sofern bspw. das Rohr wärmer ist als das Wasser. Für die Wärmestromdichte \(\dot q\) an der Grenzfläche zwischen Festkörper („Wand“) und Fluid gilt:
\begin{align}
&\boxed{\dot q = \alpha \cdot (T_W-T_F)} \\[5px]
\end{align}
Darin bezeichnet \(T_F\) die Temperatur des Fluids und \(T_W\) die Temperatur unmittelbar an der Wand des Festkörpers. Mehr Informationen zum Wärmeübergangskoeffizient finden sich im Artikel Wärmeübergangskoeffizient für Konvektion.
Der Kehrwert des Wärmeübergangskoeffizienten wird Wärmeübergangswiderstand \(R_\text{s}\) genannt:
\begin{align}
\label{rk}
&\boxed{R_\text{s} =\frac{1}{\alpha}} ~~~\text{Wärmeübergangswiderstand} \\[5px]
\end{align}
Der Wärmeübergangswiderstand beschreibt als bauteilabhängige Größe die Dämmwirkung eines Bauteils bezüglich der Wärmeströmung (Widerstand gegenüber Konvektion)!
Wärmedurchgangskoeffizient (U-Wert) und Wärmedurchgangswiderstand
Der Wärmedurchgangskoeffizient \(U\) wird auch als U-Wert bezeichnet und beschreibt den Wärmetransport zwischen zwei Fluiden, die durch einen Festkörper voneinander getrennt sind. Die Wärmestromdichte \(\dot q\) durch den Festkörper ist dabei von der Temperaturdifferenz \(\Delta T\) der Fluide abhängig:
\begin{align}
&\boxed{\dot q = U \cdot \Delta T}\\[5px]
\end{align}
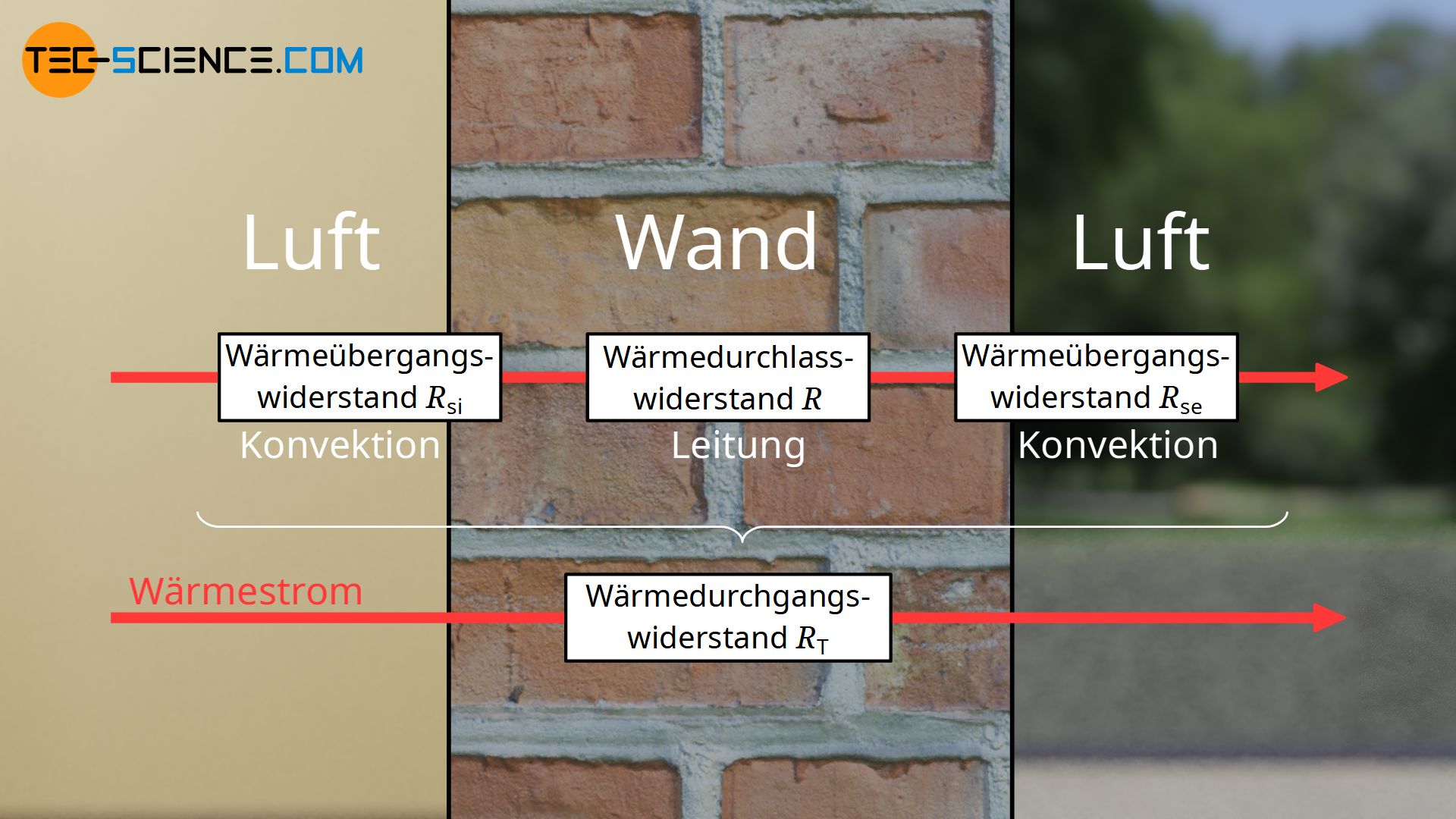
Der U-Wert spielt im Bauwesen eine große Rolle, wo bspw. eine Gebäudewand die Luft innerhalb des Gebäudes von der Luft außerhalb des Gebäudes trennt. Dabei spielen zwei Wärmeübertragungsmechanismen eine besondere Rolle, wobei sich die gesamte Wärmeübertragung in drei Schritte gliedern lässt:
- Wärmeströmung vom Fluid auf die eine Seite des Festkörpers („Innenseite“)
→ Wärmeübergangswiderstand \(R_\text{si}\) - Wärmeleitung durch den Festkörper hindurch („im Inneren“)
→ Wärmedurchlasswiderstand \(R\) - Wärmeströmung von der gegenüberliegenden Seite des Festkörpers („Außenseite“) auf das Fluid
→ Wärmeübergangswiderstand \(R_\text{se}\)
Die Summe der einzelnen Wärmewiderstände, ergibt schließlich den Gesamtwärmewiderstand durch das Bauteil (analog zu elektrischen Widerständen). Dieser Gesamtwärmewiderstand wird auch als Wärmedurchgangswiderstand \(R_\text{T}\) bezeichnet:
\begin{align}
&\boxed{R_\text{T} =R_\text{si} + R + R_\text{se}} ~~~\text{Wärmedurchgangswiderstand}\\[5px]
\end{align}
Der Wärmedurchgangswiderstand beschreibt also die Dämmwirkung eines Bauteils, welches zwei Fluide (z.B. Luft) voneinander trennt. Der Kehrwert des Wärmedurchgangswiderstands entspricht dann schließlich dem Wärmedurchgangskoeffizienten \(U\):
\begin{align}
&\boxed{U = \frac{1}{R_\text{T}} =\frac{1}{R_\text{si} + R + R_\text{se}}} ~~~\text{U-Wert}\\[5px]
\end{align}
Zusammenfassung
| Kenngröße | Beschreibung der … | Bemerkung |
|---|---|---|
| Wärme- leitfähigkeit \(\lambda\) | stationären Wärmeleitung | Stoffeigenschaft |
| Wärmedurchlass- koeffizient \(\Lambda\) | stationären Wärmeleitung | Bauteileigenschaft |
| Wärmedurchlass- widerstand \(R\) | Dämmwirkung bei Wärmeleitung | Kehrwert des Wärmedurchlass-koeffizienten |
| Temperaturleit- fähigkeit \(a\) | instationären Temperaturausbreitung durch Wärmeleitung | siehe Wärmeleitungs-gleichung |
| Wärmeübergangs- koeffizient \(\alpha\) | Wärmeströmung (Konvektion) zwischen Fluid und Feststoff | – |
| Wärmeübergangs- widerstand \(R_\text{s}\) | Dämmwirkung bei Wärmeübertragung durch Konvektion | Kehrwert des Wärmeübergangs-koeffizienten |
| Wärmedurchgangs- koeffizient \(U\) (U-Wert) | Wärmeübertragung zwischen zwei Fluiden, die durch einen Feststoff getrennt sind | Auftreten von Konvektion und Wärmeleitung gleichzeitig |
| Wärmedurchgangs- widerstand \(R_\text{T}\) | Dämmwirkung bei Wärmeübertragung zwischen zwei Fluiden, die durch einen Feststoff getrennt sind | Kehrwert des Wärmedurchgangs-koeffizienten |