Erfahre in diesem Artikel mehr zur Berechnung der Endtemperatur eines Getränkes beim Kühlen mit Eiswürfel.
Einleitung (Excel-Tabelle zur Berechnung)
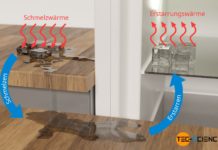
Möchte man im Sommer ein warmes Getränk relativ schnell kühlen, so nutzt man hierzu meist Eiswürfel. Der Nachteil ist allerdings, dass Erfrischungsgetränke durch das Schmelzen der Eiswürfel meist verwässert werden. Wäre es also nicht sinnvoll, Eiswürfel zu entwickeln, die nicht schmelzen? Oder könnte man nicht einfach im Gefrierschrank gekühlte Kupferwürfel nutzen?

Um diese Frage abschließend zu beantworten, wird im Folgenden zunächst gezeigt, wie die sich einstellende Endtemperatur nach vollständigem Schmelzen der Eiswürfel und Mischen des Schmelzwassers mit dem Getränk berechnet werden kann. Dabei wird vereinfachend davon ausgegangen, dass Wärme nur zwischen Getränk und Eiswürfel übertragen wird. In der Realität sind bei den stattfindenden Wärmeübertragungen auch die Umgebung und das Glas involviert, was im Folgenden allerdings vernachlässigt wird.
Der gesamte Kühlprozess durch die Eiswürfel lässt sich grundsätzlich in drei Schritte unterteilen, auf die im Folgenden näher eingegangen wird:
- Erwärmen der Eiswürfel auf Schmelztemperatur
- Schmelzen der Eiswürfel
- Mischen des Schmelzwassers mit dem Getränk

Für all diejenigen, die sich nicht mit der Herleitung der Formeln beschäftigen möchten, können die Endtemperatur mit Hilfe folgender Excel-Datei direkt berechnen lassen:
Erwärmen der Eiswürfel auf Schmelztemperatur
Eiswürfel aus dem Gefrierschrank haben in der Regel eine Temperatur von etwa -20 °C. Gibt man die Eiswürfel ins Getränk, so erwärmen sich diese zunächst bis auf Schmelztemperatur von 0 °C. Mit Hilfe der mittleren spezifischen Wärmekapazität des Eises von cE = 2,0 kJ/(kg⋅K) und der Masse mE = 50 g kann die erforderliche Wärme QE für diese Erwärmungsprozess anhand des Temperaturanstiegs von ΔTE = 20 °C ermittelt werden:
\begin{align}
&Q_\text{E} = c_\text{E} \cdot m_\text{E} \cdot \Delta T_\text{E} \\[5px]
&Q_\text{E} = 2,0 \frac{\text{kJ}}{\text{kg⋅K}} \cdot 0,05 \text{ kg} \cdot 20 \text{ °C} = 2 \text{ kJ}\\[5px]
\end{align}
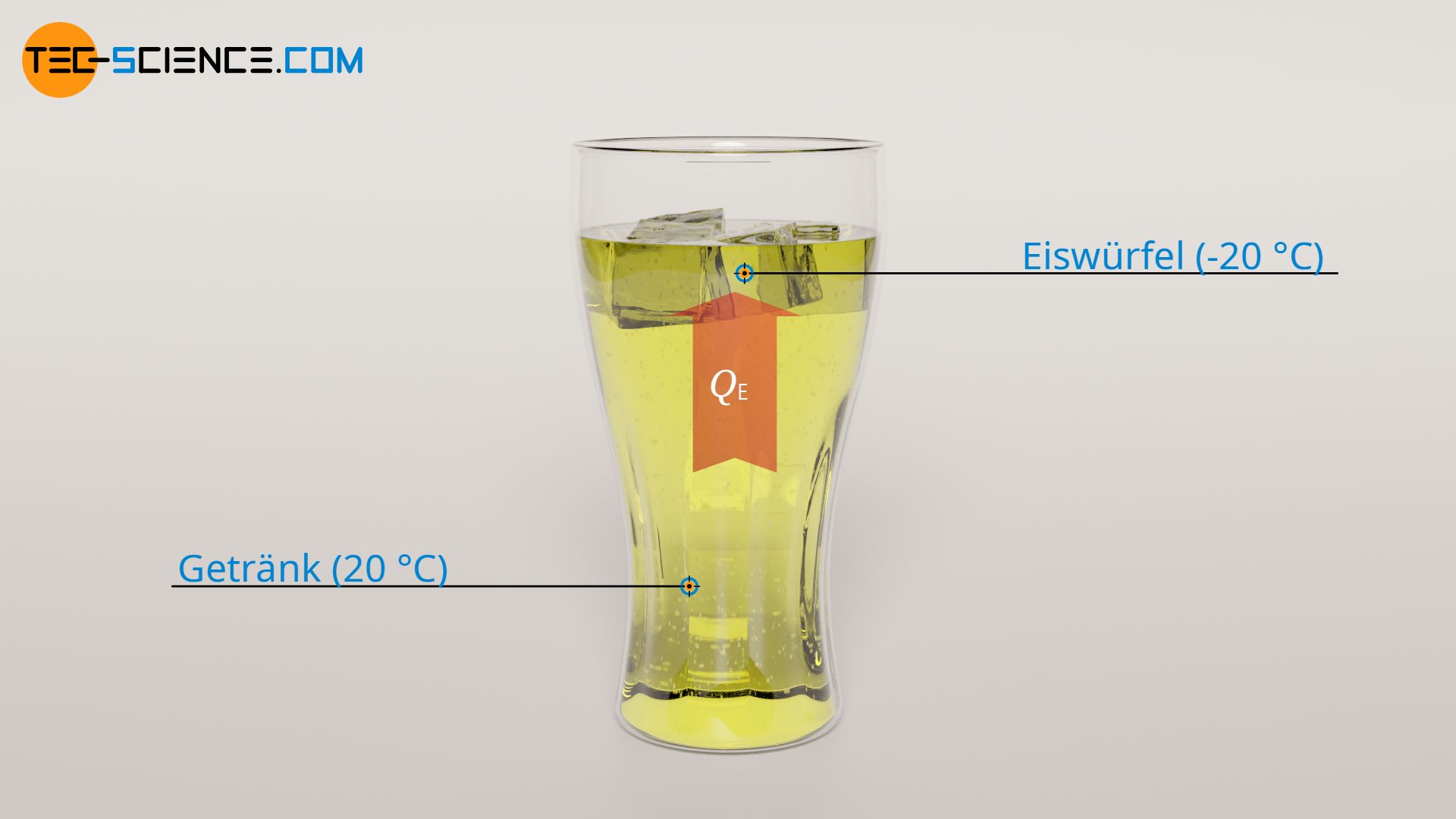
Für die Erwärmung der anfänglich -20 °C kalten Eiswürfel auf Schmelztemperatur von 0°C ist also eine Wärmeenergie von 2 kJ notwendig. Diese erforderliche Wärme wird vom Getränk geliefert. Umgekehrt bedeutet dies, dass dem Getränk zur Erwärmung der Eiswürfel 2 kJ an Wärmeenergie entzogen werden. Die Temperatur des Getränkes wird hierdurch offensichtlich geringer. Den Betrag ΔT1, um den sich die Temperatur des Getränkes durch die Abfuhr der Wärme QE verringert, kann mit Hilfe der spezifischen Wärmekapazität des Getränkes cG und der Masse des Getränkes mG ermittelt. Da die meisten Getränke nahezu vollständig aus Wasser bestehen (außer Milchgetränke), kann an dieser Stelle die spezifische Wärmekapazität von Wasser mit cG = 4,2 kJ/(kg⋅K) verwendet werden:
\begin{align}
&Q_\text{E} = c_\text{G} \cdot m_\text{G} \cdot \Delta T_\text{1} \\[5px]
&\Delta T_\text{1} = \frac{Q_\text{E}}{c_\text{G} \cdot m_\text{G}} \\[5px]
&\Delta T_\text{1} = \frac{2 \text{ kJ}}{4,2 \frac{\text{kJ}}{\text{kg⋅K}} \cdot 0,5 \text{ kg}} \approx 1 \text{ °C} \\[5px]
\end{align}
Aufgrund der Erwärmung der Eiswürfel auf Schmelztemperatur verringert sich die Temperatur des Getränkes um 1 °C. Da die Temperatur des Getränkes zu Beginn von 20 °C betrug, hat dieses folglich nun eine Temperatur von 19 °C.
Schmelzen der Eiswürfel
Sind die Eiswürfel auf Schmelztemperatur erwärmt, dann beginnen diese zu Schmelzen. Hierfür ist Schmelzwärme QS nötig. Diese kann mit Hilfe der spezifischen Schmelzwärme von Eis mit qS = 334 kJ/kg und der Masse der zu schmelzenden Eiswürfel von mE = 50 g ermittelt werden:
\begin{align}
&Q_\text{S} = q_\text{S} \cdot m_\text{E} \\[5px]
&Q_\text{S} = 334 \frac{\text{kJ}}{\text{kg}} \cdot 0,05 \text{ kg} = 16,7 \text{ kJ} \\[5px]
\end{align}
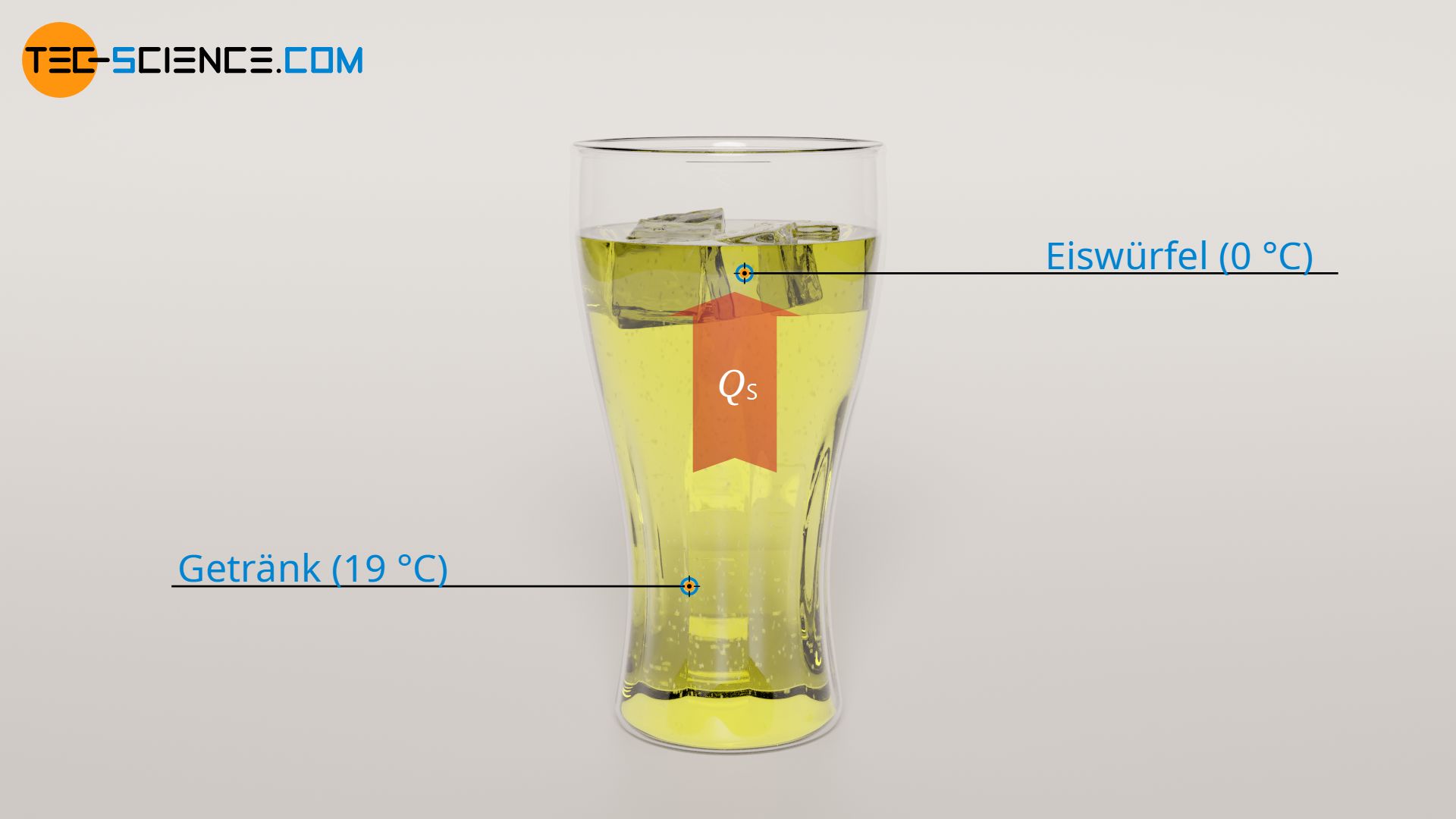
Zum vollständigen Schmelzen der Eiswürfel ist folglich eine Wärmeenergie von 16,7 kJ notwendig. Auch dieser Wärmebetrag wird vom Getränk geliefert. Somit wird dem Getränk während des Schmelzen 16,7 kJ an Wärmeenergie entzogen. Dies ist deutlich mehr als während der Erwärmung der Eiswürfel. Dementsprechend fällt auch die damit verbundene Temperaturänderung ΔT2 durch den Wärmeentzug QS des Getränkes höher aus:
\begin{align}
&Q_\text{S} = c_\text{G} \cdot m_\text{G} \cdot \Delta T_2 \\[5px]
&\Delta T_2 = \frac{Q_\text{S}}{c_\text{G} \cdot m_\text{G}} \\[5px]
&\Delta T_2 = \frac{16,7 \text{ kJ}}{4,2 \frac{\text{kJ}}{\text{kg⋅K}} \cdot 0,5 \text{ kg}} \approx 8 \text{ °C} \\[5px]
\end{align}
Aufgrund des Schmelzens der Eiswürfel verringert sich die Temperatur des Getränkes folglich nochmals um 8 °C. Da die Temperatur des Getränkes unmittelbar vor dem Schmelzen 19 °C betrug, hat dieses nun eine Temperatur von 11 °C.
Mischen der geschmolzenen Eiswürfel mit dem Getränk (Mischtemperatur)
Zwar findet während des Schmelzens der Eiswürfel gleichzeitig eine Vermischung des 0 °C kalten Schmelzwassers mit dem Getränk statt, dieser Vorgang kann energetisch jedoch getrennt betrachtet werden. Dies bedeutet, dass zunächst die Eiswürfel, wie im Abschnitt zuvor betrachtet, vollständig geschmolzen werden. Erst im Anschluss hieran wird der Mischvorgang zwischen 0 °C kaltem Schmelzwasser (TS) und 11 °C kaltem Getränk betrachtet (TG). Dieser Mischvorgang kann mit Hilfe der Richmann’schen Mischungsregel beschrieben werden:
\begin{align}
\boxed{T_\text{M} = \frac{c_\text{G} \cdot m_\text{G} \cdot T_\text{G} + c_\text{S} \cdot m_\text{S} \cdot T_\text{S}}{c_\text{G} \cdot m_\text{G} + c_\text{S} \cdot m_\text{S}}} ~~~\text{Richmann’sche Mischungsregel} \\[5px]
\end{align}
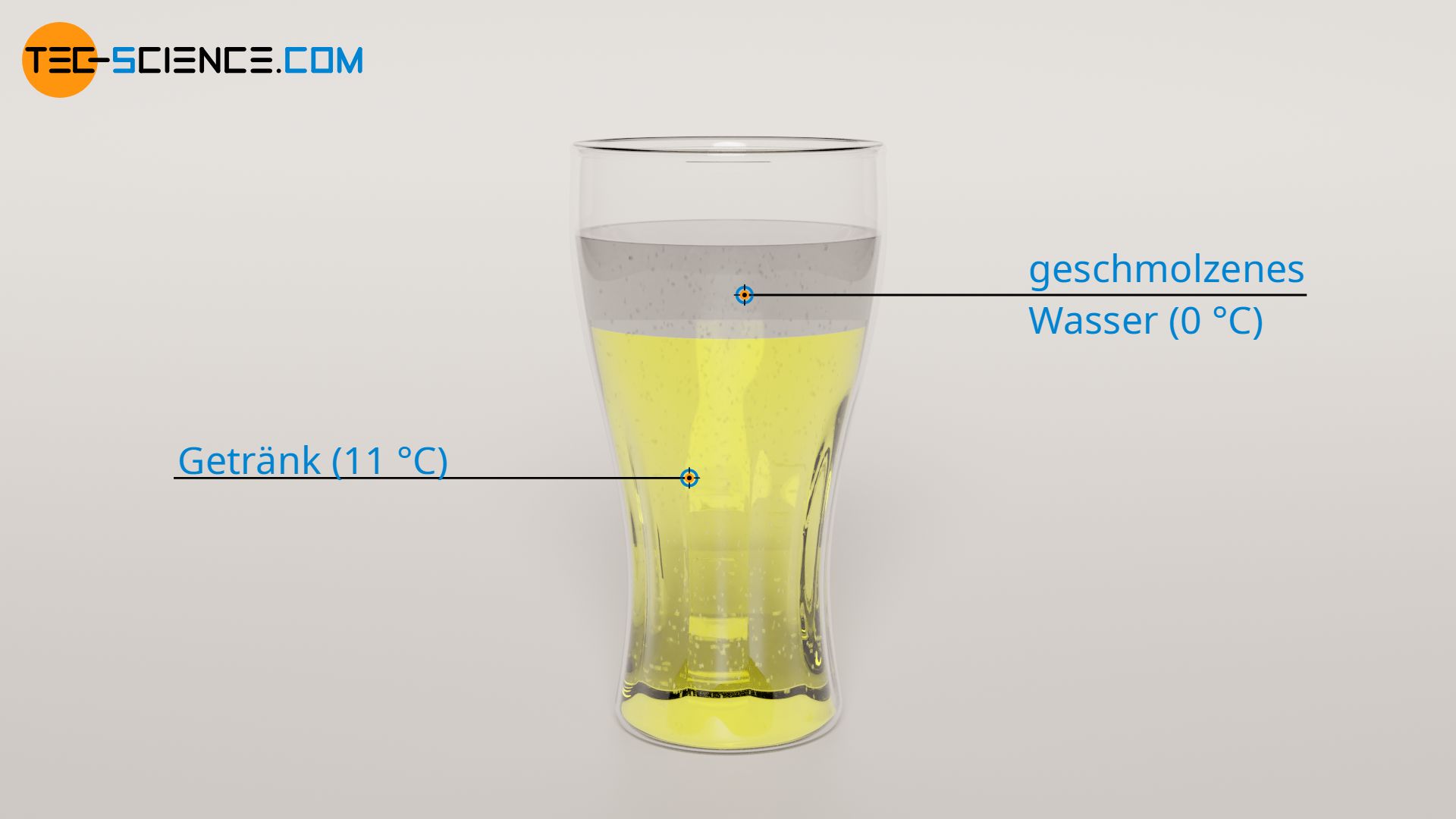
Für die spezifische Wärmekapazität der geschmolzenen Eiswürfel cS wird, wie für das Getränk auch, die spezifische Wärmekapazität von Wasser mit cS = 4,2 kJ/(kg⋅K) zugrunde gelegt (in diesem Fall kürzen sich die spezifischen Wärmekapazitäten in der oberen Formel sogar heraus). Die Masse des Schmelzwassers mS entspricht dabei der Masse der Eiswürfel mit mS = 50 g. Die endgültige Mischtemperatur TM lässt sich damit wie folgt ermitteln:
\begin{align}
\require{cancel}
&T_\text{M} = \frac{\cancel{c_\text{G}} \cdot m_\text{G} \cdot T_\text{G} + \cancel{c_\text{S}} \cdot m_\text{S} \cdot T_\text{S}}{\cancel{c_\text{G}} \cdot m_\text{G} + \cancel{c_\text{S}} \cdot m_\text{S}} \\[5px]
&T_\text{M} = \frac{ m_\text{G} \cdot T_\text{G} + m_\text{S} \cdot T_\text{S}}{m_\text{G} + m_\text{S}} \\[5px]
&T_\text{M} = \frac{ 0,5 \text{ kg} \cdot 11 \text{ °C} + 0,05 \text{ kg} \cdot 0 \text{ °C}}{0,5 \text{ kg} + 0,05 \text{ kg}} = 10 \text { °C} \\[5px]
\end{align}
Durch den Mischvorgang fällt die Temperatur des Getränkes also nochmals um ΔT3 = 1 °C auf insgesamt 10 °C.
Schlussfolgerung
Betrachtet man den in drei Schritten gegliederten Abkühlungsvorgang des Getränkes, dann zeigt sich in den jeweiligen Fällen folgende Temperaturänderung des Getränkes:
- Temperaturänderung durch Erwärmen der Eiswürfel: ΔT1 = 1 °C
- Temperaturänderung durch Schmelzen der Eiswürfel: ΔT2 = 8 °C
- Temperaturänderung durch Mischen des Schmelzwassers: ΔT3 = 1 °C
Die größte Temperaturänderung ist folglich auf den Schmelzvorgang der Eiswürfel zurückzuführen. Dies liegt an der relativ großen Schmelzwärme von Wasser (bzw. Eis) im Vergleich zu den geringen Wärmemengen, die während des Erwärmens der Eiswürfel bzw. dem Mischen übertragen werden. Es ist also für die Kühlwirkung wesentlich, dass die Eiswürfel schmelzen! Insofern muss immer ein Kompromiss eingegangen werden zwischen der gewünschten Kühlung und der zulässigen Verwässerung des Getränkes durch die geschmolzenen Eiswürfel.

Würde man anstelle der Eiswürfel die erwähnten Kupferwürfel nutzen, die man im Gefrierschrank auf -20 °C abkühlt, erhielte man lediglich eine Endtemperatur von 16,7 °C. Beachte, dass Kupfer offensichtlich nicht schmilzt, wenn man es in ein Getränk gibt. Insofern handelt es sich dabei lediglich um einen „Mischungsvorgang“, der mit der Richmann’schen Mischungsregel beschrieben werden kann. Die Kupferwürfel haben eine spezifische Wärmekapazität von 0,385 kJ/(kg⋅K) und eine Masse von 0,488 kg (bei identischem Volumen wie die 50-Gramm-Eiswürfel):
\begin{align}
\require{cancel}
&T_\text{M} = \frac{c_\text{G} \cdot m_\text{G} \cdot T_\text{G} + c_\text{Cu} \cdot m_\text{Cu} \cdot T_\text{Cu}}{c_\text{G} \cdot m_\text{G} + c_\text{Cu} \cdot m_\text{Cu}} \\[5px]
&T_\text{M} = \frac{ 0,5 \text{ kg} \cdot 4,2 \frac{\text{kJ}}{\text{kg⋅K}} \cdot 20 \text{ °C} + 0,488 \text{ kg} \cdot 0,385 \frac{\text{kJ}}{\text{kg⋅K}} \cdot (-20 \text{ °C})}{0,5 \text{ kg} \cdot 4,2 \frac{\text{kJ}}{\text{kg⋅K}} + 0,488 \text{ kg} \cdot 0,385 \frac{\text{kJ}}{\text{kg⋅K}}} \\[5px]
&T_\text{M} = 16,7 \text{ °C} \\[5px]
\end{align}