Die Expansion eines idealen Gases gegen ein Vakuum in einem adiabaten System ist ein isothermer Prozess!
Im Artikel zum isentropen Prozess wurde bereits angedeutet, dass die oft gleichgesetzte Bezeichnung „adiabatischer Prozess“ an mancher Stelle irreführend sein kann und im allgemeinen nicht korrekt ist. Um dies zu verdeutlichen wird im Folgenden die Expansion eines idealen Gases gegen ein Vakuum betrachtet.
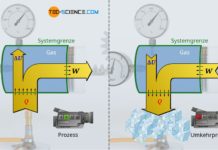
Man stelle sich hierzu ein Gas in einem Zylinder vor, das mit einem beweglichen (masselosen) Kolben reibungsfrei verschlossen ist. Der Kolben wird zunächst mit einer Kraft in Stellung gehalten. Der Zylinder selbst befinde sich in einer evakuierten Kammer, sodass um ihn herum ein Vakuum herrscht. Zylinder und Kolben sollen perfekt wärmeisoliert sein. Es handelt sich demzufolge um ein adiabates System. Nun wird der Kolben losgelassen und das Gas expandiert folglich gegen das Vakuum.

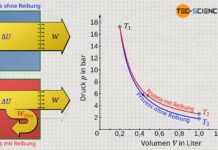
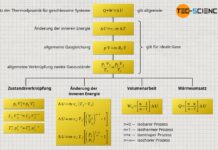
Nur weil der vorliegende Zylinder ein adiabates System bildet, bedeutet dies in diesem Fall allerdings nicht, dass die hergeleiteten Gesetzmäßigkeiten des vermeintlich „adiabaten Prozesses“ angewendet werden können! So sollte nach diesen Gesetzmäßigkeiten die Temperatur bei einer Expansion mit größer werdendem Volumen sinken (T⋅Vκ-1=konstant). Dies wird man bei der vorliegenden Expansion gegen das Vakuum allerdings nicht beobachten! Das überraschende Ergebnis dieser Expansion zeigt sich, wenn man den ersten Hauptsatz der Thermodynamik zur Hilfe nimmt:
\begin{align}
\underbrace{W}_{=0} + \underbrace{Q}_{=0} = \Delta U = 0
\end{align}

Da es sich um ein adiabates System handelt, wird dem Gas per Definition keine Energie in Form von Wärme zu- oder abgeführt (Q=0). Zudem verrichtet das Gas keine Arbeit (W=0), denn schließlich expandiert das Gas gegen ein Vakuum. Das Gas muss folglich keinerlei Kraft aufwenden, um den (masselosen) Kolben gegen den nicht vorhandenen Umgebungsdruck zu verschieben. Es existiert sozusagen kein Gegendruck, gegen den das Gas „ankämpfen“ muss. Folglich muss das Gas für die Expansion des Volumens keine Arbeit verrichten. Wird jedoch keine Energie in Form von Wärme oder Arbeit am System umgesetzt, so bleibt die innere Energie folglich konstant (ΔU=0).
Da die innere Energie für ein ideales Gas direkt mit der Temperatur verknüpft ist (und diese sich nicht ändert), handelt es sich bei der vorliegenden freien Expansion gegen das Vakuum also um eine isotherme Zustandsänderung! Überraschenderweise bleibt die Temperatur bei diesem Prozess folglich konstant und nimmt nicht ab.
Bei der Expansion eines idealen Gases in einem adiabaten System entgegen eines Vakuums bleibt die Temperatur konstant (isothermer Prozess)!
Anmerkung: Dass die Temperatur bei der Expansion gegen das Vakuum konstant bleibt, gilt lediglich für ideale Gase. Für reale Gase wird man hingegen eine leichte Verringerung der Temperatur feststellen. Dies bezeichnet man dann auch als Joule-Thomson-Effekt.
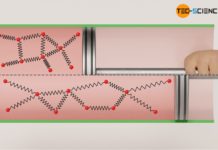
Man kann sich diesen isothermen Expansionsvorgang auch ganz anschaulich erklären. Man stelle sich hierzu vor man befände sich in einem Vakuum und hielte wild umherfliegende Teilchen in der Hand. Öffnet man nun die Hand, dann fliegen die Teilchen in das Vakuum und werden letztlich durch keine weiteren Teilchen abgebremst (da der Kolben im oberen Beispiel als masselos betrachtet wird, kann man diesen ohnehin weggedacht vorstellen und die Teilchen frei in das Vakuum strömen lassen – dies ist dieselbe Situation). Die Teilchen behalten also ihre kinetische Energie bei. Da die kinetische Energie der Teilchen direkt mit der Temperatur verknüpft ist, bedeutet dies letztlich eine unveränderte Temperatur.
Das adiabatische Expandieren eines idealen Gases in ein Vakuum stellt ein isothermer Prozess dar!
Dieses Beispiel macht deutlich, dass sich Zustandsänderungen von adiabaten Systemen nicht notwendigerweise nach den Gesetzmäßigkeiten des isentropen Prozesses beschreiben lassen. Deshalb sollte im Zusammenhang mit den dafür hergeleiteten Isentropengleichungen auch nicht unbedingt von adiabatischen Prozessen gesprochen werden. Denn dies suggeriert fälschlicherweise, dass bei allen adiabaten Systemen diese Gleichungen verwendet werden könnten. Das soeben beschriebene Expansionsbeispiel widerlegt jedoch genau dies.
Es schließt sich natürlich die Frage an, unter welcher Bedingung sich die Zustandsänderung eines adiabates Systems dann tatsächlich durch die hergeleiteten Gleichungen beschreiben lässt bzw. wann eben nicht. Die Antwort hierauf wird findet sich im Artikel Reversibilität von thermodynamischen Prozessen (Entropie).