Dissipation von Energie in geschlossenen Systemen

Erfahre in diesem Artikel, warum bei Vorgängen mit Reibung, die Volumenänderungsarbeit des Gases nicht dem vom System verrichteten Arbeit entspricht.

Volumenänderungsarbeit (Volumenarbeit)

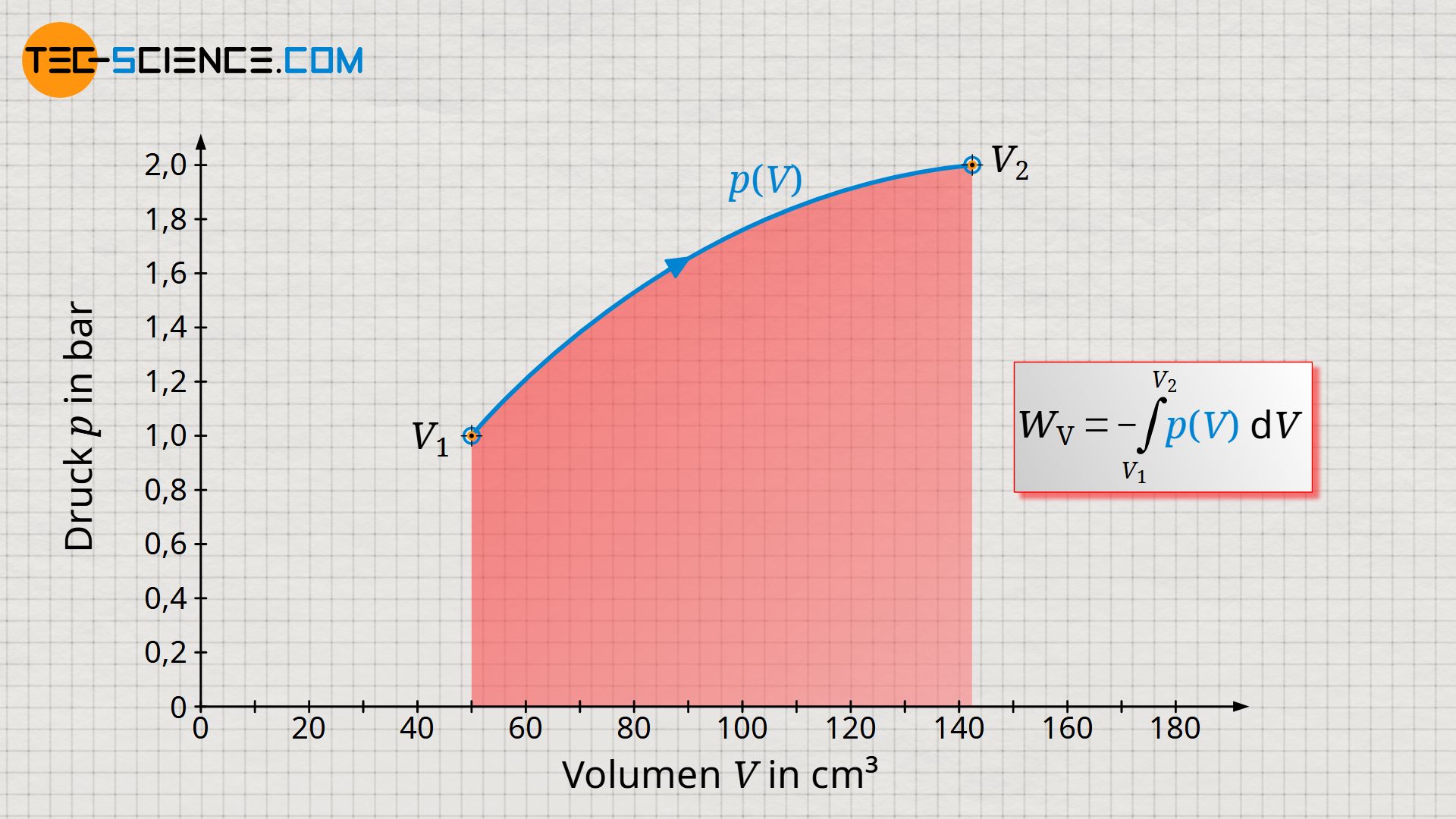
Im Artikel Volumenänderungsarbeit wurde ausführlich erläutert, dass die vom Gas oder am Gas verrichtete Arbeit bei einem thermodynamischen Prozess, der Fläche unter der Zustandskurve in einem Volumen-Druck-Diagramm entspricht. Hierzu stellen wir uns ein Gas in einem Zylinder vor, welches mit einem Kolben verschlossen ist. Durch Erwärmung des Gases wird über eine Zahnstange und ein Zahnrad ein dabei ein Gewicht angehoben.

Der thermodynamische Prozess gestaltet sich im Volumen-Druck-Diagramm wie abgebildet. Die Arbeit, die das Gas am Kolben verrichtet entspricht der Volumenänderungsarbeit (Volumenarbeit) des Gases, welche sich als Fläche unter der Kurve ergibt.

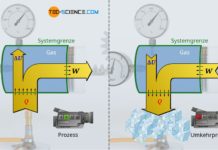
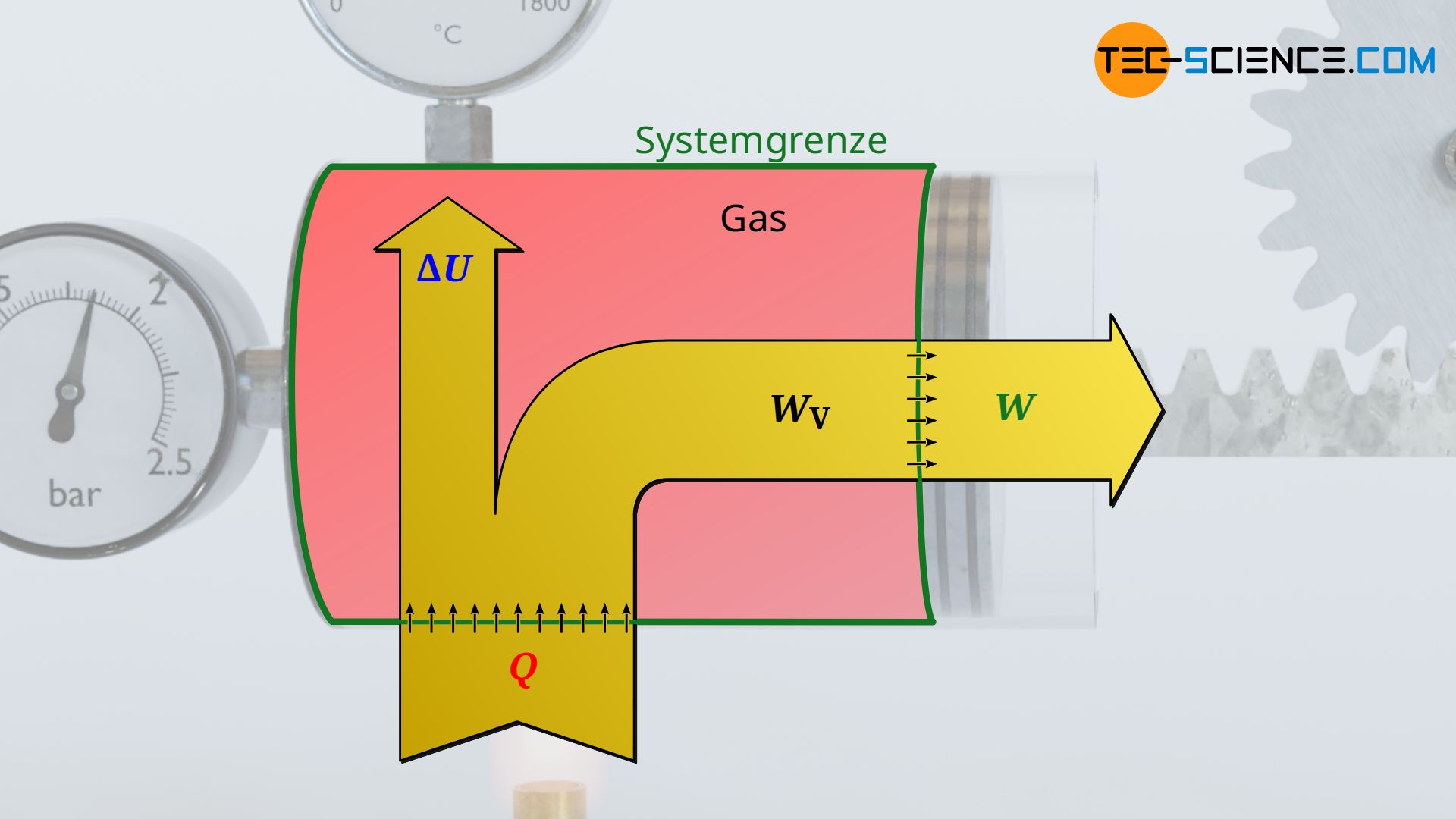
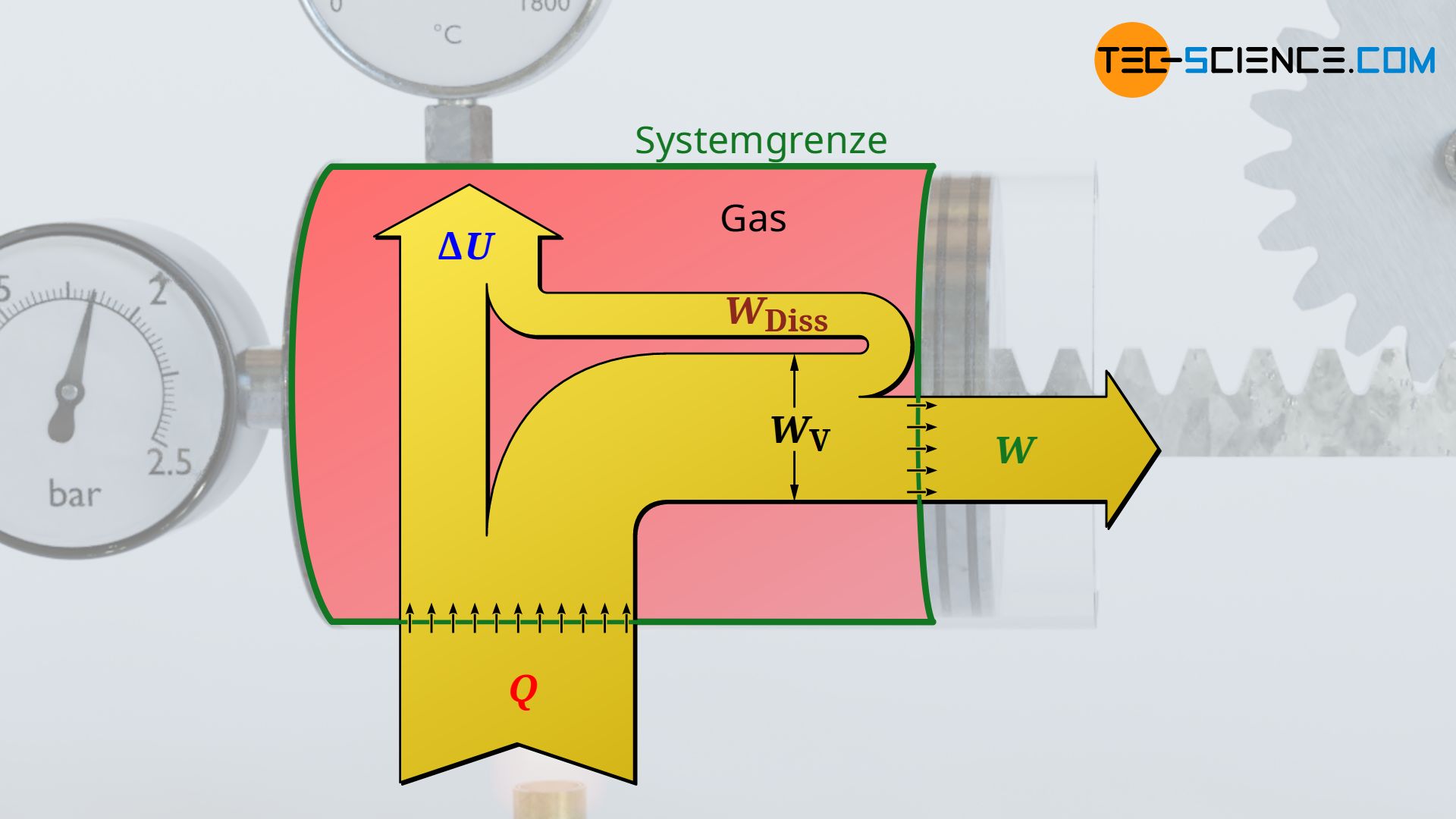
Die vom Gas verrichtete Volumenarbeit entspricht allerdings nicht zwangsweise dem Arbeitsumsatz, den das System dann über die Kolbenstange nach außen abgibt. Dies wird lediglich bei einem reibungsfreien Vorgang der Fall sein. Tritt hingegen Reibung zwischen Kolben und Zylinderwand auf, so wird nicht mehr die gesamte vom Gas erbrachte Volumenänderungsarbeit nach außen an den Kolben abgegeben. Ein solcher reibungsbehafteter Prozess wird im Folgenden näher betrachtet.

Volumenarbeit ≠ abgegebene Arbeit

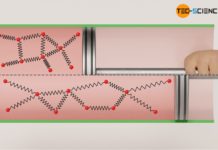
Für den Fall dass Reibung zwischen Kolben und Zylinderwand herrscht, schiebt der Gasdruck zwar den Kolben mit jener Volumenänderungsarbeit aus die sich als Fläche unter der Zustandskurve im Volumen-Druck-Diagramm ergibt. Dieser Arbeitsumsatz kommt allerdings nicht vollständig an der Kolbenstange an, da ein Teil dieser Volumenarbeit (Ausschiebearbeit) durch Reibung „verloren“ geht. Das System gibt bei reibungsbehafteten Vorgängen also nicht mehr die gesamte vom Gas erbrachte Volumenänderungsarbeit W_V nach außen ab, sondern nur jenen Teil abzüglich der im Inneren aufzuwendenden Reibungsarbeit W_Diss:

\begin{align}
\label{1}
&\boxed{W = W_\text{V} + W_\text{Diss}} ~~~\text{nach außen über die Systemgrenze abgegebene Arbeit}
\end{align}

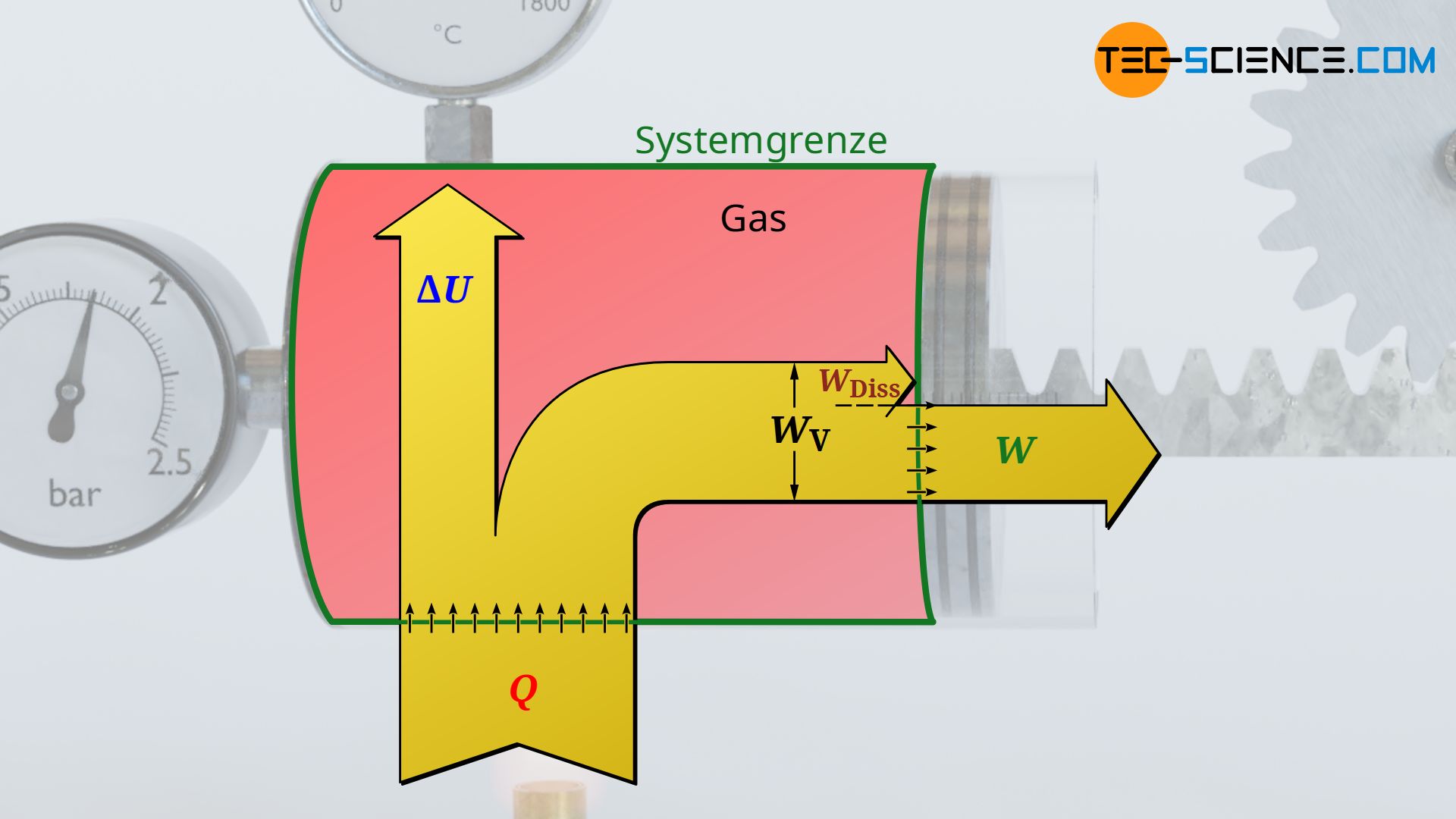
Man darf sich an dieser Stelle nicht vom Pluszeichen in der Gleichung verwirren lassen! Dieses ergibt sich lediglich aufgrund der Vorzeichenkonvention. So wird bei einer Expansion die negative Volumenarbeit W_V durch die positive Reibungsarbeit W_Diss betragsmäßig verringert. Es verbleit somit nur noch ein geringerer (negativer) Arbeitsumsatz (W<0), der nach außen abgegeben wird.

Erhöhung der inneren Energie durch Dissipation von Energie

Wenn das Gas im reibungsbehafteten Fall also eine größere Volumenänderungsarbeit erbringt als nach außen abgegeben wird, wohin verschwindet dann der Restbetrag, d.h. die Reibungsarbeit W_Diss?

Die Reibungsarbeit führt letztlich zur Erhöhung der inneren Energie des Systems. Dies lässt sich in der Praxis daran erkennen, dass reibungsbehaftete Prozesse mit größeren Temperaturen verbunden sind als reibungsfreie Vorgänge. Beachte, dass bei idealen Gasen die innere Energie direkt mit der Temperatur verknüpft ist (siehe hierzu Artikel Berechnung der inneren Energie für ideale Gase). Eine höhere innere Energie bedeutet somit immer auch eine höhere Temperatur!

Umgangssprachlich würde man an dieser Stelle wahrscheinlich sagen:

„Reibung wird in Wärme umgewandelt und sorgt somit für höhere Temperaturen.“

Diese Aussage ist aufgrund des falsch verwendeten Wärmebegriffs zwar fachsprachlich nicht korrekt, bringt es bezüglich der Temperaturerhöhung jedoch auf den Punkt. Fachsprachlich korrekt muss die Aussage lauten, dass Reibungsarbeit der inneren Energie des Gases zugutekommt und damit die Temperaturerhöhung bewirkt! Die Reibungsarbeit wird sozusagen in innere Energie „zerstreut“. Deshalb bezeichnet man die Reibungsarbeit auch ganz allgemein als Dissipationsarbeit W_Diss (vom Lateinischen dissipare für zerstreuen).

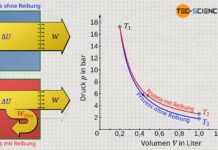
Beachte, dass die erhöhte innere Energie bei reibungsbehafteten Vorgängen stets größere Temperaturen und damit auch höhere Drücke zur Folge haben. Dementsprechend erhöht sich das Druckniveau während der Expansion und führt somit schließlich zu einer größeren Volumenänderungsarbeit im Vergleich zum reibungsfreien Fall. Vergleiche hierzu die Flächen unter den Zustandskurven für den reibungsfreien bzw. reibungsbehafteten Expansionsvorgang, welche jeweils die Volumenarbeit veranschaulichen!

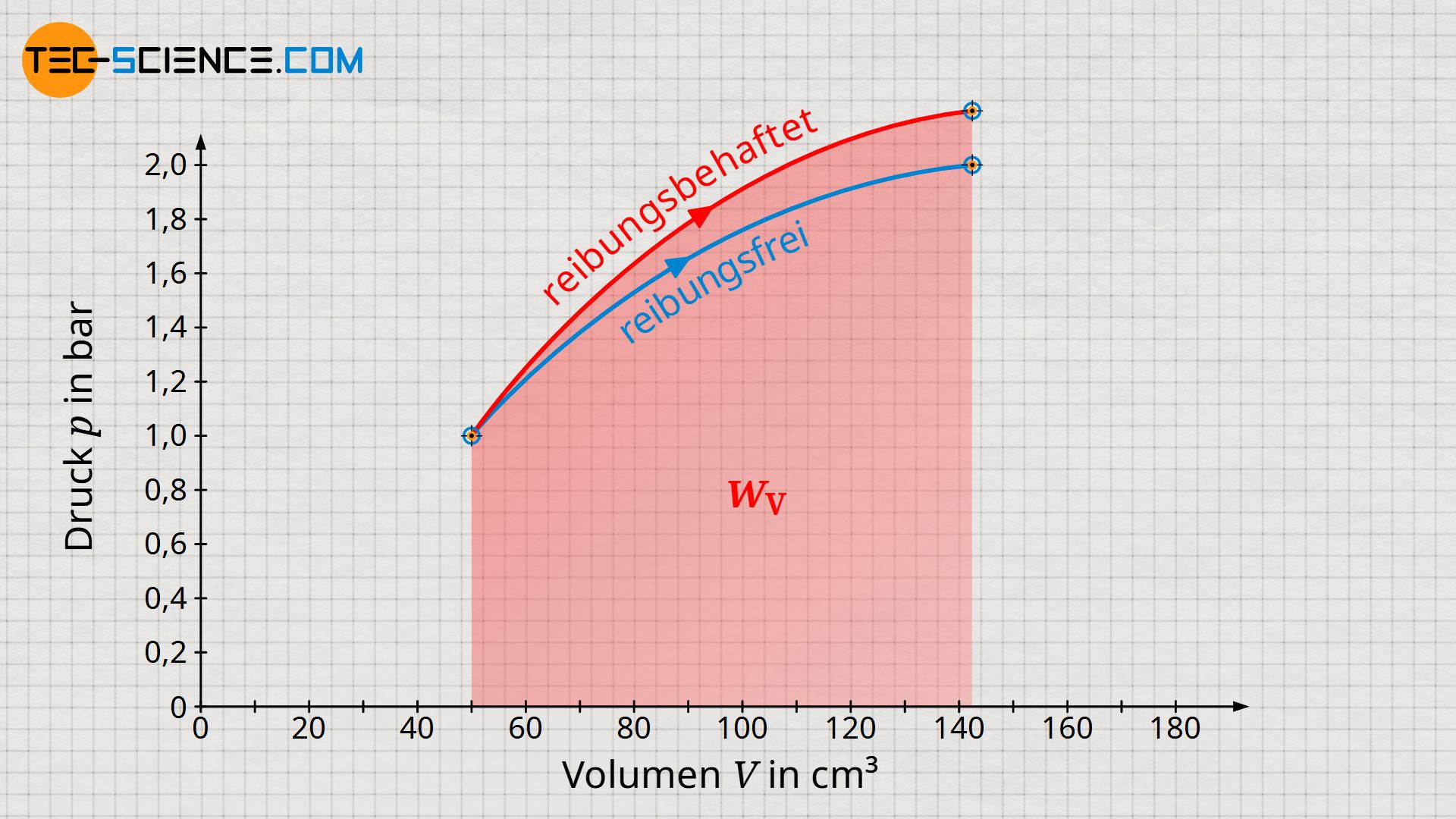
Die größere Volumenänderungsarbeit bei der reibungsbehafteten Expansion darf an dieser Stelle aber nicht über die Tatsache hinwegtäuschen, dass diese ja nicht im vollen Maße nach außen abgegeben wird. Nach außen abgegeben wird nur jener Teil der Volumenänderungsarbeit welcher abzüglich der Dissipationsarbeit übrig bleibt. Trotz höherer Volumenarbeit wird im reibungsbehafteten Fall also stets ein geringerer Energiebetrag nach außen abgegeben als im reibungsfreien Fall.

Expansion vs. Kompression

Gleichung (\ref{1}) gilt im Übrigen nicht nur für einen Expansionsvorgang, sondern auch für einen Kompressionsvorgang. So bringt diese Gleichung vorzeichenrichtig zum Ausdruck, dass bei einer reibungsbehafteten Kompression mehr Arbeit W>0 von außen aufgewendet werden muss im Vergleich zum reibungsfreien Fall. Denn dann muss nicht mehr nur das Gasvolumen entgegen des Gasdrucks komprimiert werden (Volumenänderungsarbeit W_V>0), sondern es muss zusätzlich auch noch die Reibungsarbeit aufgewendet werden (W_Diss>0). Die positive Volumenänderungsarbeit und positive Reibungsarbeit ergeben somit eine größere Arbeit W>0, die dem System von außen über die Systemgrenze zuzuführen ist. Auch hierbei wird die Reibungsarbeit W_Diss wieder in innere Energie dissipiert, was zu einer höheren Temperatur im Vergleich zum reibungsfreien Fall führt.

Diese Betrachtungen machen deutlich, dass Dissipationsarbeiten stets die innere Energie eines Gases erhöhen; unabhängig davon ob es sich um einen Expansionsvorgang oder um einen Kompressionsvorgang handelt. Deshalb gehen Dissipationsenergien grundsätzlich immer mit einem positiven Vorzeichen in die Energiebilanzierung ein!

Beachte, dass im Allgemeinen also stets unterschieden werden muss zwischen:

• der Volumenarbeit W_V als Arbeit, die im Inneren des Systems am Gas bzw. vom Gas verrichtet wird und
• der Arbeit W, die tatsächlich über die Systemgrenze in das System bzw. aus dem System gelangt.

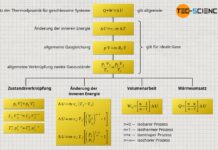
Erster Hauptsatz der Thermodynamik

Der erste Hauptsatz der Thermodynamik bilanziert grundsätzlich nur die Energieströme über die Systemgrenze hinweg, d.h. die Wärme Q und die Arbeit W (nicht die Volumenarbeit im inneren des Systems!):

\begin{align}
\label{0}
&\boxed{W + Q = \Delta U} ~~~\text{gilt allgemein} \\[5px]
\end{align}

Jedoch lässt sich die Volumenänderungsarbeit W_V und die Dissipationsarbeit W_Diss mit Hilfe von Gleichung (\ref{1}) explizit in den ersten Hauptsatz (\ref{0}) aufnehmen:

\begin{align}
\label{2}
&\boxed{W_\text{V} + W_\text{Diss} + Q = \Delta U} ~~~\text{gilt allgemein} \\[5px]
\end{align}

Beachte, dass nur unter der Voraussetzung eines reibungsfrei ablaufenden Prozesses, d.h. ohne Dissipation von Energie (W_Diss=0), die Volumenänderungsarbeit W_V auch tatsächlich der vom bzw. am System umgesetzten Arbeit W entspricht:

\begin{align}
\label{3}
&\boxed{W_\text{V} + Q = \Delta U} ~~~\text{gilt nur reibungsfreie Prozesse} \\[5px]
\end{align}