Technische Arbeit (Wellenarbeit) in offenen Systemen

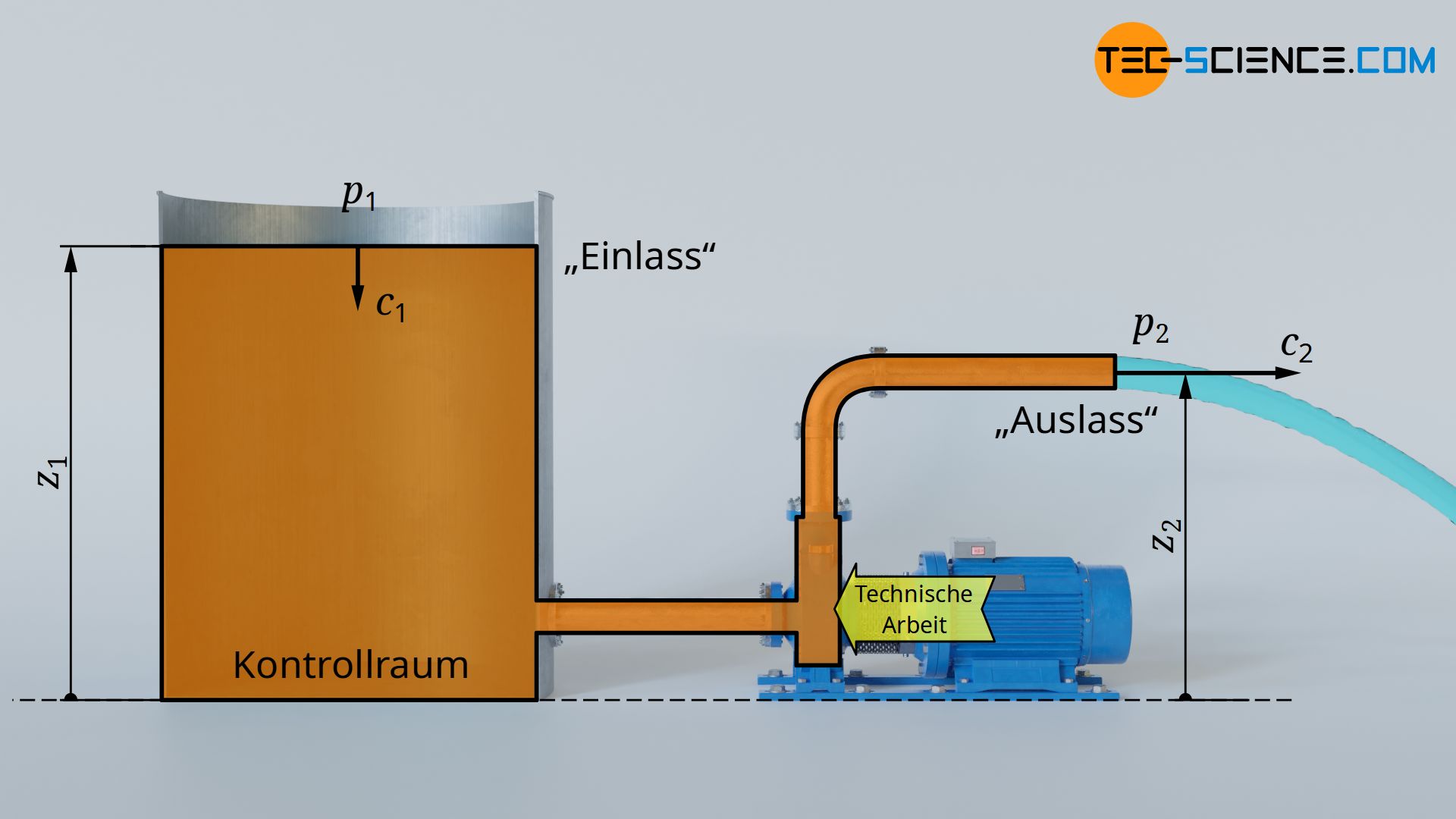
Als technische Arbeit bezeichnet man die insgesamt in offenen Systemen verrichtete Arbeit, welche meist über Wellen zu- bzw. abgeführt wird.

Druckänderungsarbeit

Im Artikel zur Druckänderungsarbeit beschränkte sich die in offenen System (z.B. in Verdichtern oder Pumpen) umgesetzte Arbeit lediglich auf die Druckänderungsarbeit. Dabei wurde davon ausgegangen, dass das offene System lediglich für das Durchschieben des Fluids (Verschiebearbeit) und für die Volumenänderung des Fluids (Volumenänderungsarbeit) Arbeit aufbringen muss. Diese als Druckänderungsarbeit W_D bezeichnete Arbeit eines offenen Systems kann durch folgendes Integral ermittelt werden:

\begin{align}
\label{7410}
W_\text{D} = \int\limits_{p_1}^{p_2}V(p)~\text{d}p
\end{align}

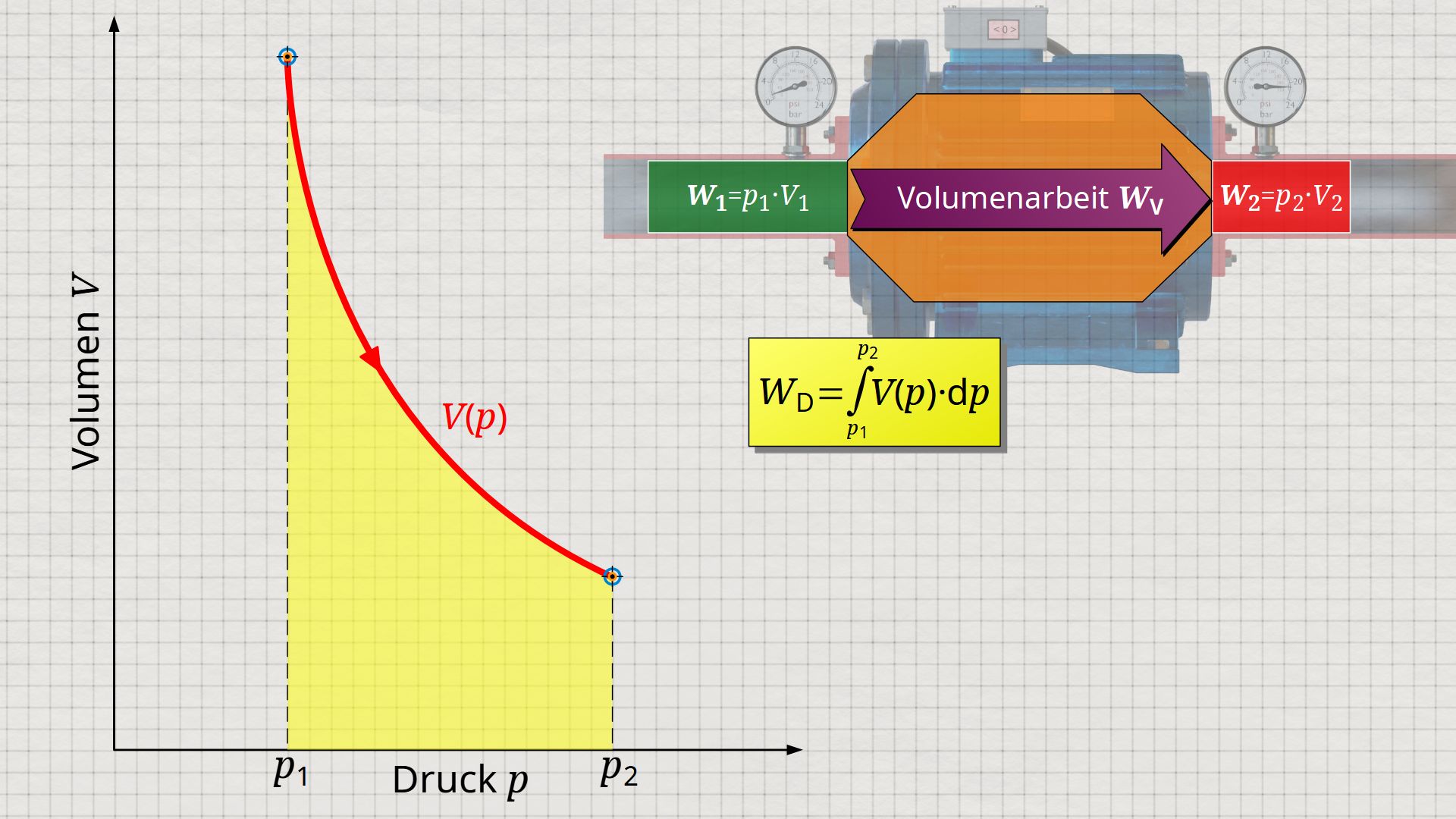
Darin bezeichnet V(p) der Verlauf des Volumens eines eingeschobenen Fluidelementes in Abhängigkeit des Drucks, wenn dieses durch das offene System strömt.

Neben der Druckänderungsarbeit finden in einem offenen System im Allgemeinen jedoch noch weitere energetische Prozesse statt, die mit einem Aufwand an Arbeit verbunden sind. Am Beispiel einer Wasserpumpe soll dies im Folgenden exemplarisch erläutert werden.

Beschleunigungsarbeit

Wir betrachten eine Pumpe, bei der der Einlassquerschnitt größer ist als der Auslassquerschnitt. Dennoch strömt im stationären Fall innerhalb einer bestimmten Zeit dieselbe Masse durch den kleineren Auslassquerschnitt wie durch den größeren Einlassquerschnitt. Diese Tatsache ist der Erhaltung der Masse geschuldet (Kontinuitätsbedingung), denn im stationären Betrieb kann sich keine Masse auf Dauer in der Pumpe ansammeln oder vernichtet werden. Es wird also dieselbe Menge an Wasser in die Pumpe durch den Einlassquerschnitt eintreten wie im selben Moment am Auslassquerschnitt wieder austritt.

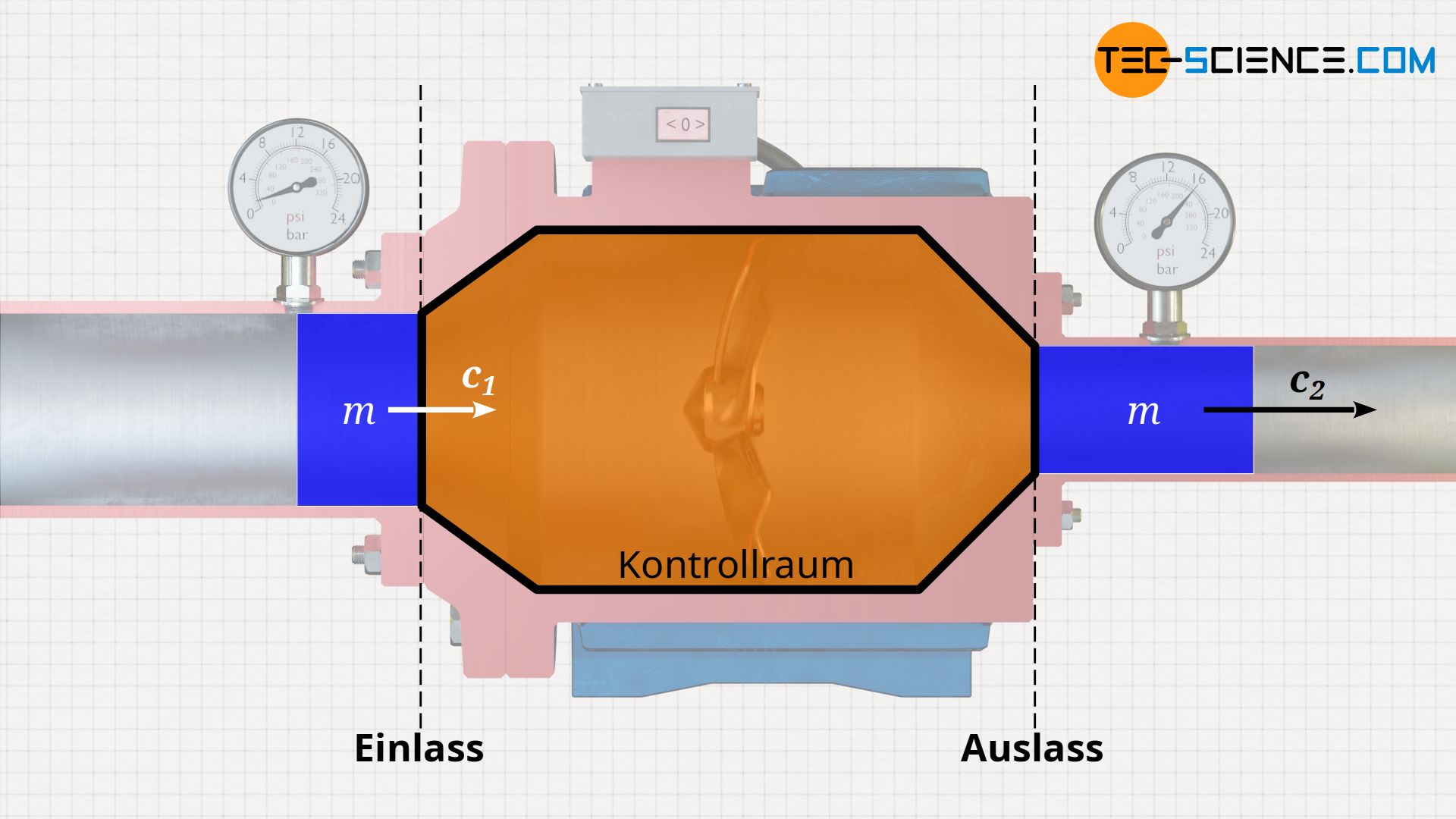
Da der Auslassquerschnitt jedoch kleiner ist, muss die dortige Wassermasse folglich mit höherer Geschwindigkeit hindurchströmen. Nur so kann in derselben Zeit dieselbe Wassermasse wie am Eingang hindurchströmen. Dieses Phänomen kennt man auch aus der Alltagserfahrung: Drückt man einen offenen Gartenschlauch am vorderen Ende etwas zusammen und verringert dadurch den Querschnitt, so strömt das Wasser mit größerer Geschwindigkeit aus.

Demnach muss ein betrachtetes Fluidelement der Masse m beim Hindurchströmen durch die Pumpe von der Einströmgeschwindigkeit c₁ auf die Ausströmgeschwindigkeit c₂ beschleunigt werden. Die Pumpe hat zusätzlich zur Druckänderungsarbeit W_D also auch noch die Beschleunigungsarbeit W_B aufzuwenden:

\begin{align}
\label{6723}
\boxed{W_\text{B} = \tfrac{1}{2}~m~\Delta c^2} ~~~\text{mit}~~~ \Delta c^2 = c_2^2 – c_1^2
\end{align}

Anmerkung: Bei identischen Ein- und Ausgangsquerschnitte muss für inkompressible Medien wie Flüssigkeiten keine Beschleunigungsarbeit aufgewandt werden, da sich hierbei die Geschwindigkeiten nicht ändern werden. Bei kompressiblen Medien wie Gasen wird sich die Durchströmgeschwindigkeit jedoch auch bei gleichen Ein- und Ausgangsquerschnitten ändern! Denn schließlich wird hierbei die betrachtete Gasmasse mit deutlich unterschiedlichem Volumen ausgeschoben, was wiederum andere Geschwindigkeiten bedingt, um den Massenstrom konstant zu halten.

Hubarbeit

In den bisherigen Betrachtungen war der Einlass der Pumpe auf derselben Höhe wie der Auslass. Dies muss aber nicht zwangsläufig der Fall sein! Im Allgemeinen sind Ein- und Auslass auf unterschiedlichen Höhen. Bei Kreiselpumpen liegt der Pumpenausgang meist höher als der Pumpeneingang. Diese Höhendifferenz bedingt einen weiteren Arbeitsaufwand der Pumpe.

Das Wasser muss nun nicht mehr einfach nur entgegen des wirkenden Druckunterschieds zwischen Ein- und Auslass durch die Pumpe durchgeschoben werden muss, sondern die hindurchströmende Wassermasse m muss entgegen der Schwerkraft um die Höhendifferenz Δz=z₂-z₁ angehoben werden. Die Pumpe muss folglich auch noch Hubarbeit W_H verrichten:

\begin{align}
\label{2735}
\boxed{W_\text{H} = m~g~\Delta z} ~~~\text{mit}~~~ \Delta z = z_2-z_1
\end{align}

Technische Arbeit

Das Durchströmen der Wassermasse durch die Pumpe wird aufgrund der Viskosität des Fluids in der Realität nicht reibungsfrei ablaufen. Schließlich werden die Wassermassen an der Innenwandung der Pumpe reiben. Und auch die Reibung in den Lagern muss zusätzlich überwunden werden. Folglich muss die Pumpe auch noch diese Reibungsarbeit W_Diss (Dissipationsarbeit) aufbringen.

All die oben genannten Arbeitsumsätze, d.h. die Summe aus

• Druckänderungsarbeit W_D (= Verschiebearbeit + Volumenänderungsarbeit),
• Beschleunigungsarbeit W_B,
• Hubarbeit W_H und
• Dissipationsarbeit W_Diss (Reibungsarbeit),

müssen von der Pumpe aufgewendet werden. Man könnte in diesem Fall zwar von Pumpenarbeit reden, jedoch muss es sich bei einem offenen System nicht immer um eine Pumpe handeln. Deshalb spricht man ganz allgemein von der technischen Arbeit W_t, die das offene System insgesamt aufzuwenden hat (z.B. bei Pumpen) oder abzugeben hat (z.B. bei Turbinen). Die technische Arbeit wird von offenen Systemen in der Regel kontinuierlich umgesetzt. Diese Energieumsetzung geschieht häufig über Wellen. So wird bei Pumpen die technische Arbeit über die Pumpenwelle zugeführt und bei Wasserturbinen über die Turbinenwelle abgeführt. Aus diesem Grund wird die technische Arbeit auch häufig als Wellenarbeit bezeichnet.

\begin{align}
\label{8918}
&W_\text{t} = W_\text{D} +W_\text{B} +W_\text{H} +W_\text{Diss} \\[5px]
\label{e8761}
&\boxed{W_\text{t} = \int\limits_{p_1}^{p_2}V(p)~\text{d}p + \tfrac{1}{2}~m~\Delta c^2 + m~g~\Delta z + W_\text{Diss}} ~~~~~\text{technische Arbeit} \\[5px]
\end{align}

bzw. als spezifische technische Arbeit w_t ausgedrückt (technische Arbeit pro Masseneinheit):

\begin{align}
\label{9228}
\boxed{w_\text{t} = \int\limits_{p_1}^{p_2}v(p)~\text{d}p + \tfrac{1}{2}~\Delta c^2 + g~\Delta z + w_\text{Diss}} ~~~~~\text{spezifische technische Arbeit}
\end{align}

Schließlich kann die technische Leistung P_t aus der spezifischen technischen Arbeit w_t multipliziert mit dem Massenstrom m‘, der durch das offene System bewegt wird, berechnet werden (siehe zur Herleitung auch den Abschnitt Verschiebeleistung):

\begin{align}
\label{4794}
\boxed{P_\text{t} = w_\text{t} ~\dot{m}}
\end{align}

Anmerkung: Bisher wurden als offene Systeme lediglich Pumpen bzw. Verdichter betrachtet. Diese werden unter Aufwand von technischer Arbeit betrieben. Das Prinzip kann aber auch umgekehrt werden, d.h. offene Systeme können auch technische Arbeit nach außen abgeben. Eine solche Umsetzung findet sich zum Beispiel in durchströmten Wasserturbinen oder Dampfturbinen wieder. Diese geben über die Turbinenwelle mechanische Arbeit nach außen ab. Die bisher betrachteten Gleichungen können prinzipiell für jedes offene System angewandt werden.

Wahl der Systemgrenzen

Beachte, dass die in den oberen Gleichungen angegebenen Strömungsgeschwindigkeiten c und Höhen z jeweils an den offenen Systemgrenzen definiert sind, wenn die betrachtete Masse in den Kontrollraum ein- bzw. ausströmt. Dies gilt im Übrigen auch für die angegebenen Drücke in der Druckänderungsarbeit. Diese Größen sind immer an den Kontrollraumgrenzen definiert.

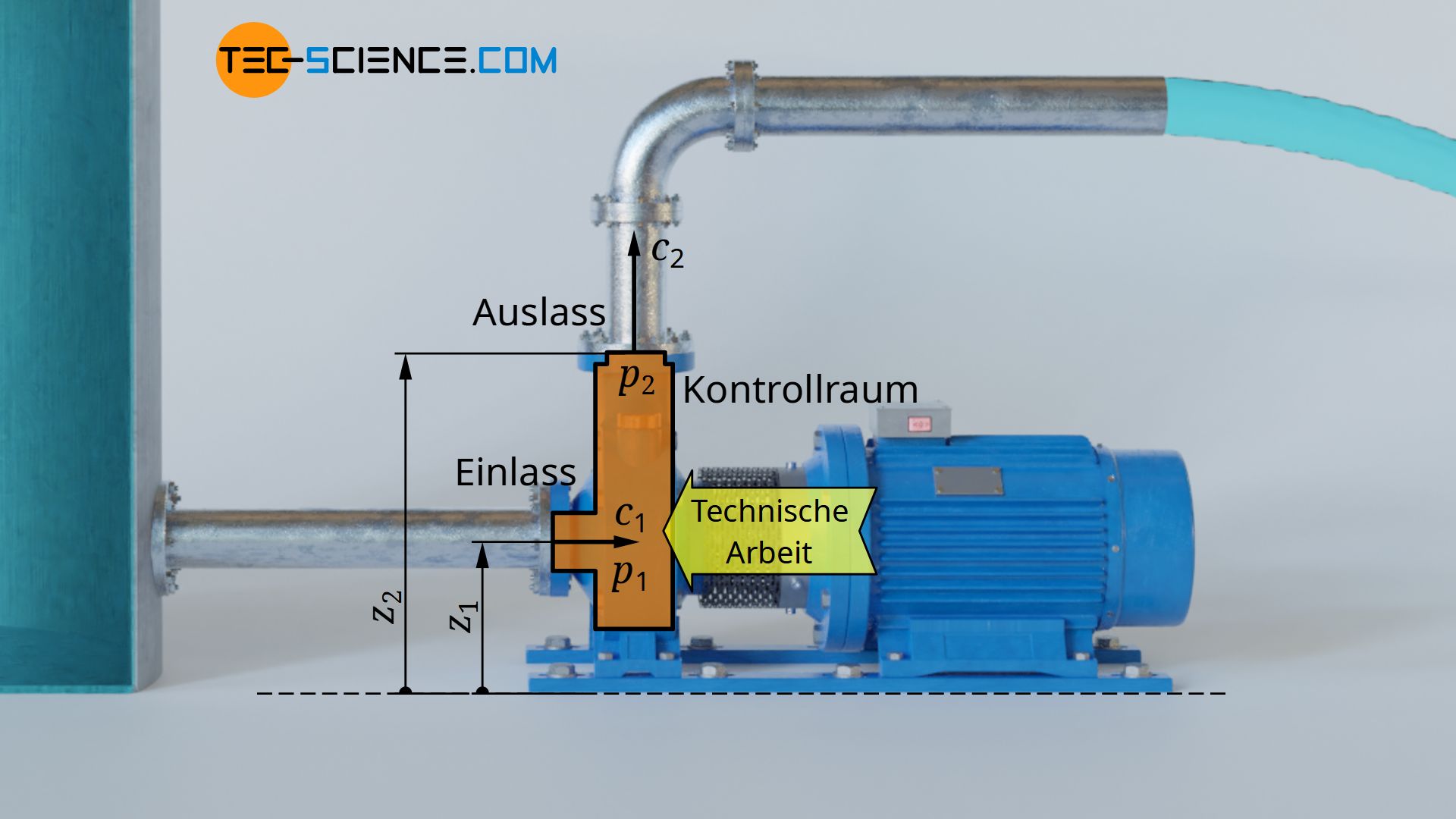
Je nach Wahl der Systemgrenze, können sich somit gänzlich unterschiedliche Werte für die jeweiligen Größen ergeben. So wäre es auch möglich, das gesamte Rohrleitungssystem und den Wassertank noch in die Betrachtung als Teil des offenen Systems miteinzubeziehen. Die Systemgrenzen wären dann an der Oberfläche des Wassertanks und am Rohrende. Dieser Betrachtung lägen folglich ganz andere Drücke, Volumina, Strömungsgeschwindigkeiten und Lagehöhen an den beiden offenen Systemgrenzen zugrunde!