Druckänderungsarbeit als Volumenänderungsarbeit von geschlossenen Systemen

Die Druckänderungsarbeit in offenen Systemen lässt sich als Volumenänderungsarbeit von geschlossenen Systemen interpretieren.

Druckänderungsarbeit

Wie im Artikel zur Druckänderungsarbeit ausführlich erläutert, setzt sich die Druckänderungsarbeit W_D aus der Summe von Verschiebearbeit W_S und Volumenänderungsarbeit W_V zusammen:

\begin{align}
\label{5715}
&W_\text{D} = W_\text{V} + W_\text{S} \\[5px]
\label{4461} 
&\boxed{W_D = – \int\limits_{V_1}^{V_2}p(V)~\text{d}V + p_2~V_2 – p_1~V_1 }
\end{align}

Am Beispiel einer kontinuierlich arbeitenden Pumpe bzw. eines Kompressors wurde das Zustandekommen der einzelnen Terme näher erläutert. Im Folgenden sollen die einzelnen Terme in Gleichung (\ref{4461}) jedoch anhand eines diskontinuierlich arbeitenden Kolbenverdichters näher diskutiert werden. Der Kolbenverdichter bietet den didaktischen Vorteil, dass die einzelnen thermodynamischen Vorgänge (Einsaugen, Verdichte und Ausstoßen) zeitlich nacheinander ablaufen und anschaulich nachvollzogen werden können.

Funktionsweise eines Kolbenverdichters

Der Kolbenverdichter besteht im Prinzip aus einem Zylinder, der mit einem Einlass- und Auslassventil versehen ist. In dem Zylinder selbst bewegt sich ein elektrisch angetriebener Kolben auf und ab. Zunächst strömt bei sich zurückziehendem Kolben und geöffnetem Einlassventil Luft in den Zylinder. Anschließend wird die Luft bei geschlossenen Ventilen verdichtet. Nach dem Verdichtungsvorgang wird das Auslassventil geöffnet. Dieses Auslassventil verbindet den Zylinder mit einem großen Druckbehälter, in dem die verdichtete Luft gesammelt wird.

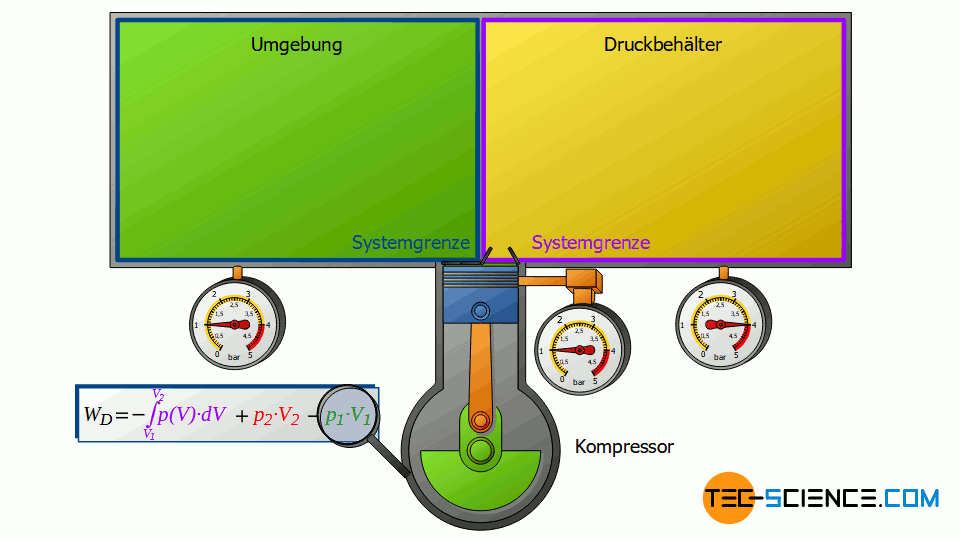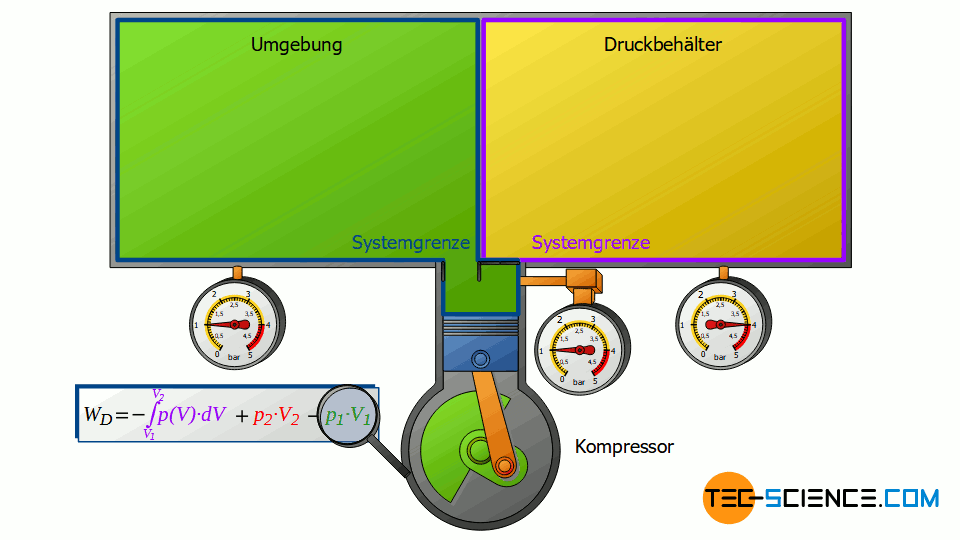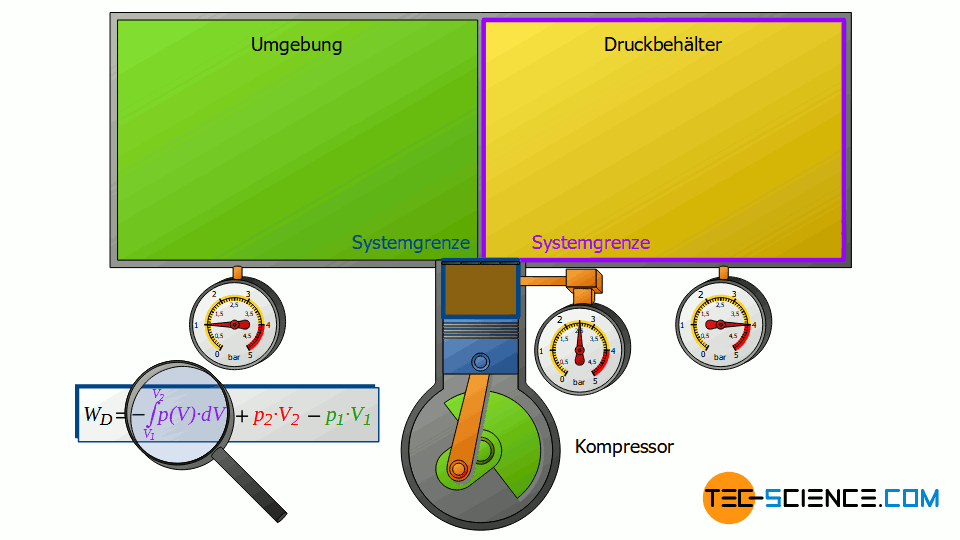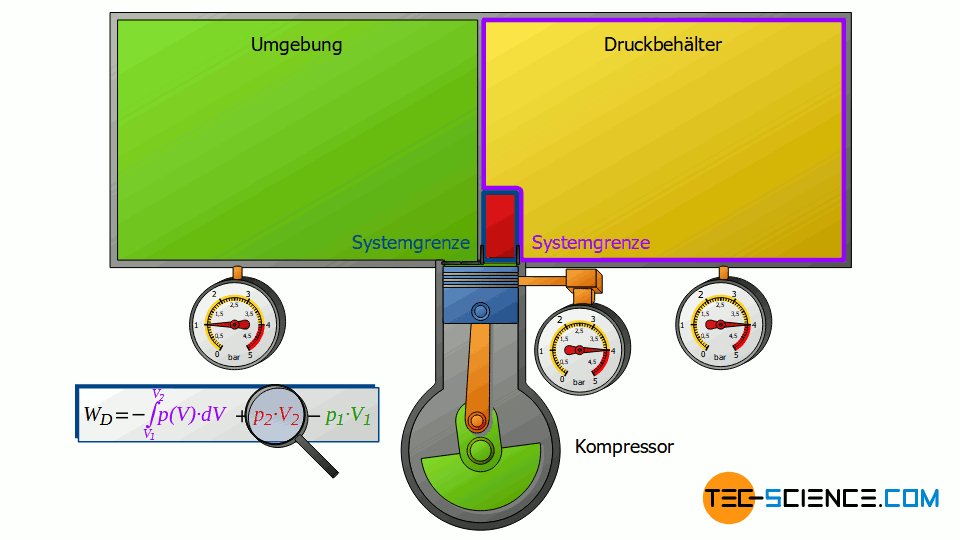
Der Druck im Druckbehälter wird dadurch konstant gehalten, dass bei Druckluftentnahme aus dem Sammelbehälter der Kolbenverdichter sofort wieder anspringt und verdichtete Luft nachliefert. Somit kommt es im Idealfall gar nicht erst zu einem Druckabfall im Druckbehälter. Das Auslassventil des Verdichters öffnet genau dann, wenn der Druck im Zylinder genauso groß ist wie der Druck im Druckbehälter, sodass die verdichtete Luft bei konstantem Druck aus dem Zylinder ausgeschoben wird.

Thermodynamische Beschreibung

Das Einsaugen, Verdichten und Ausschieben der Luft untersuchen wir im Folgenden nun etwas genauer. Dabei betrachten wir das Einsaugen und Ausstoßen jedoch nicht aus Sicht der eingesaugten bzw. ausgestoßenen Luft, sondern aus Sicht Umgebung bzw. des Druckbehälters.

Einsaugen

Zunächst saugt der Verdichter Luft aus jenem Raum an, in dem sich der Verdichter befindet – zum Beispiel aus einem Kellerraum, dessen Fenster und Türen geschlossen sind. Die Umgebung bildet somit ein geschlossenes System (im Prinzip ist der Ort, an dem der Kompressor steht, unerheblich, da die gesamte Erde ebenfalls als geschlossene System betrachtet werden könnte). Zieht sich der Kolben des Verdichters nun zurück, so wird das Volumen der geschlossenen Umgebung letztlich um das Volumen des Zylinders V₁ vergrößert.

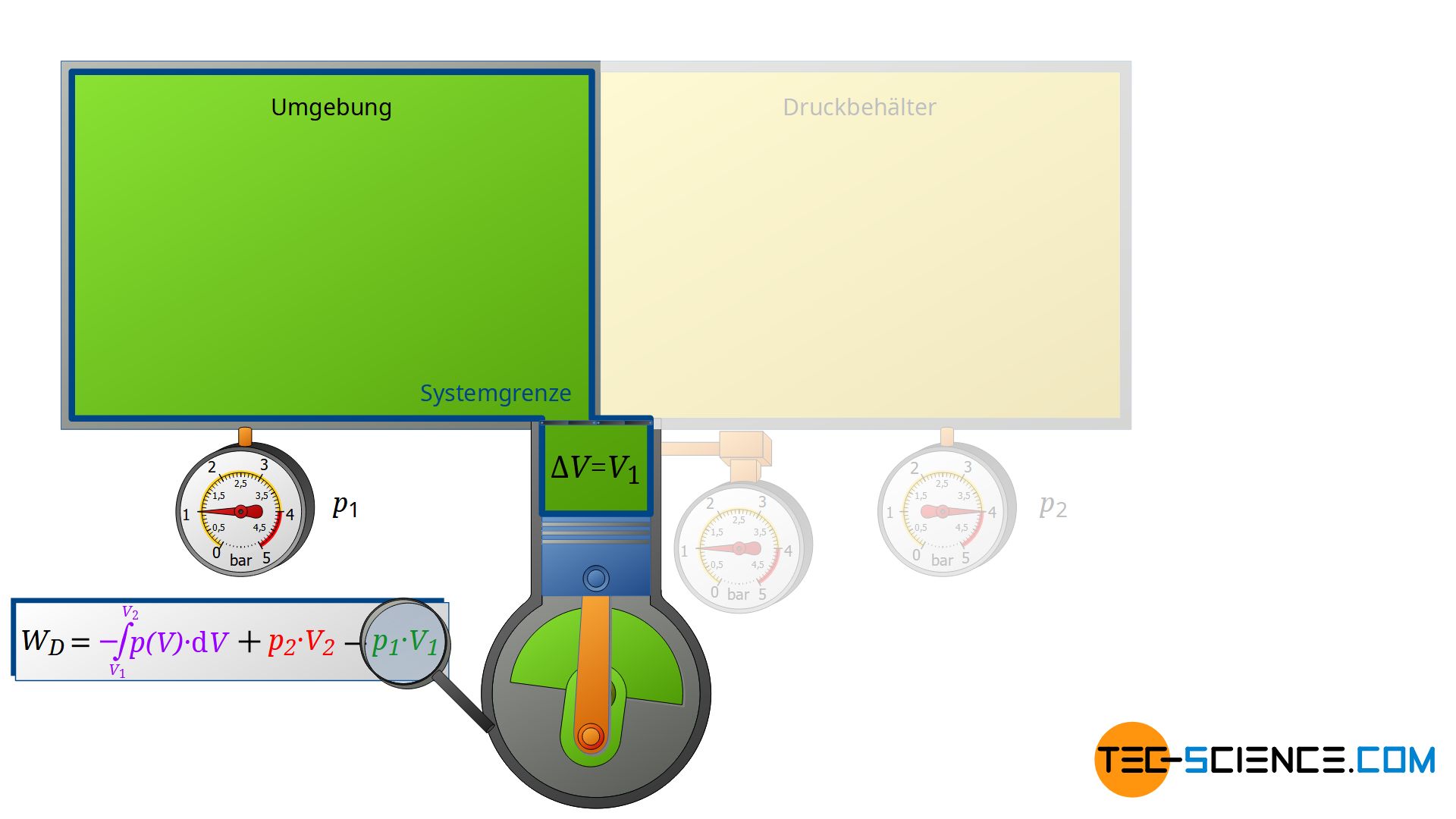
Dieser Expansionsvorgang der Umgebungsluft kann dabei als isobar angenommen werden, da sich der Druck im Kellerraum währenddessen praktisch nicht ändern wird. Die Umgebungsluft im geschlossenen Kellerraum expandiert also bei konstantem Druck p₁, wobei sich das Volumen der Umgebung um ΔV = V₁ vergrößert. Folglich wird die Volumenänderungsarbeit W₁=-p₁⋅V₁ von der Umgebung verrichtet (dieser Arbeitsumsatz ist negativ, da von der betrachteten Umgebungsluft Arbeit verrichtet wird):

\begin{align}
\label{8780}
W_1= -p_1~V_1
\end{align}

Ausschieben

Nun betrachten wir die Zustandsänderung nach dem Verdichten, d.h. wenn die verdichtete Luftmasse in den Druckluftbehälter ausgeschoben wird. Dabei wird der Druckluftbehälter wiederum als geschlossenes System angesehen. Die bereits im Behälter befindliche Druckluft kann man sich als in einer gedanklichen Blase befindlich vorstellen. Wird das vom Verdichter kommende (komprimierte) Volumen V₂ nun in den Druckluftbehälter eingeschoben, so wird die darin gedachte Druckluftblase um dieses Volumen zusammengeschoben. Das Volumen der Druckluftblase verringert sich folglich um das Volumen V₂.

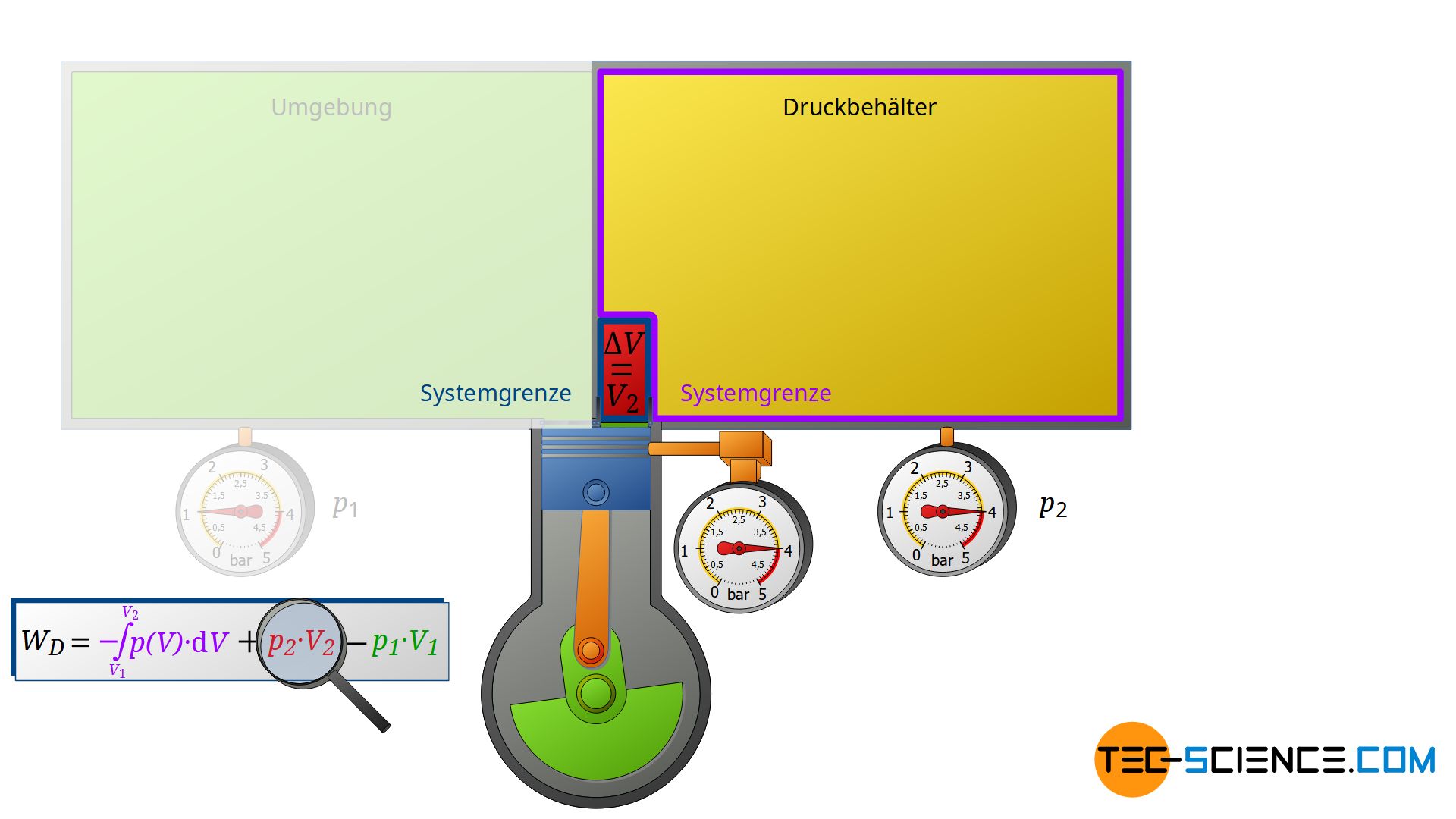
Auch dabei kann dieser Kompressionsvorgang wieder als isobar angenommen werden, wenn der Sammelbehälter nur groß genug ist. Dann wird nämlich der geringe Zustrom nicht wesentlich den Druck im Sammelbehälter ändern. Die Luft im geschlossenen Druckluftbehälter wird also bei konstantem Druck p₂ komprimiert, wobei sich das Volumen um ΔV = V₂ verringert. Dementsprechend wird die Volumenänderungsarbeit W₂=p₂⋅V₂ an der Luft im Druckbehälter verrichtet (dieser Arbeitsumsatz ist positiv, da am betrachteten Gas im Behälter Arbeit verrichtet wird):

\begin{align}
\label{eq:8844}
W_2 = p_2~V_2
\end{align}

Energieänderung der Luft in der Umgebung und im Druckbehälter

Der Energiegehalt der Luft in der Umgebung ändert sich folglich um die Volumenänderungsarbeit W₁, während sich der Energiegehalt der Luft im Druckluftbehälters um W₂ ändert. Ursache dieser Änderungen ist offensichtlich das offene System, das letztlich die Summe beider Volumenänderungsarbeiten zu verantworten hat. Die Änderung des Energiegehaltes ist auf das Ein- bzw. Ausschieben der Luft zurückzuführen und entspricht somit der Verschiebearbeit W_S des offenen Systems:

\begin{align}
\label{6852}
W_\text{S} = W_2+W_1=p_2~V_2-p_1~V_1
\end{align}

Dieses Beispiel zeigt, dass sich die Verschiebearbeit eines offenen Systems als Volumenänderungsarbeit von äußeren, geschlossenen Systemen interpretieren lässt, die mit dem offenen System gekoppelt sind! Das offene System (Verdichter) überträgt sozusagen Energie von einem geschlossenen System (Umgebung) auf ein anderes geschlossenes System (Druckbehälter).

Energieänderung der Luft im Verdichter

Der Verdichter ändert aber nicht nur den Energiegehalt der beiden äußeren Systeme, sondern auch noch den Energiegehalt der eingesaugten Luftmasse, d.h. jener Luftmasse, die durch das offene System geschoben wird. Deshalb muss der Verdichtungsvorgang der angesaugten Luftmasse von V₁ auf V₂ für eine Energiebilanzierung ebenfalls mitberücksichtigt werden.

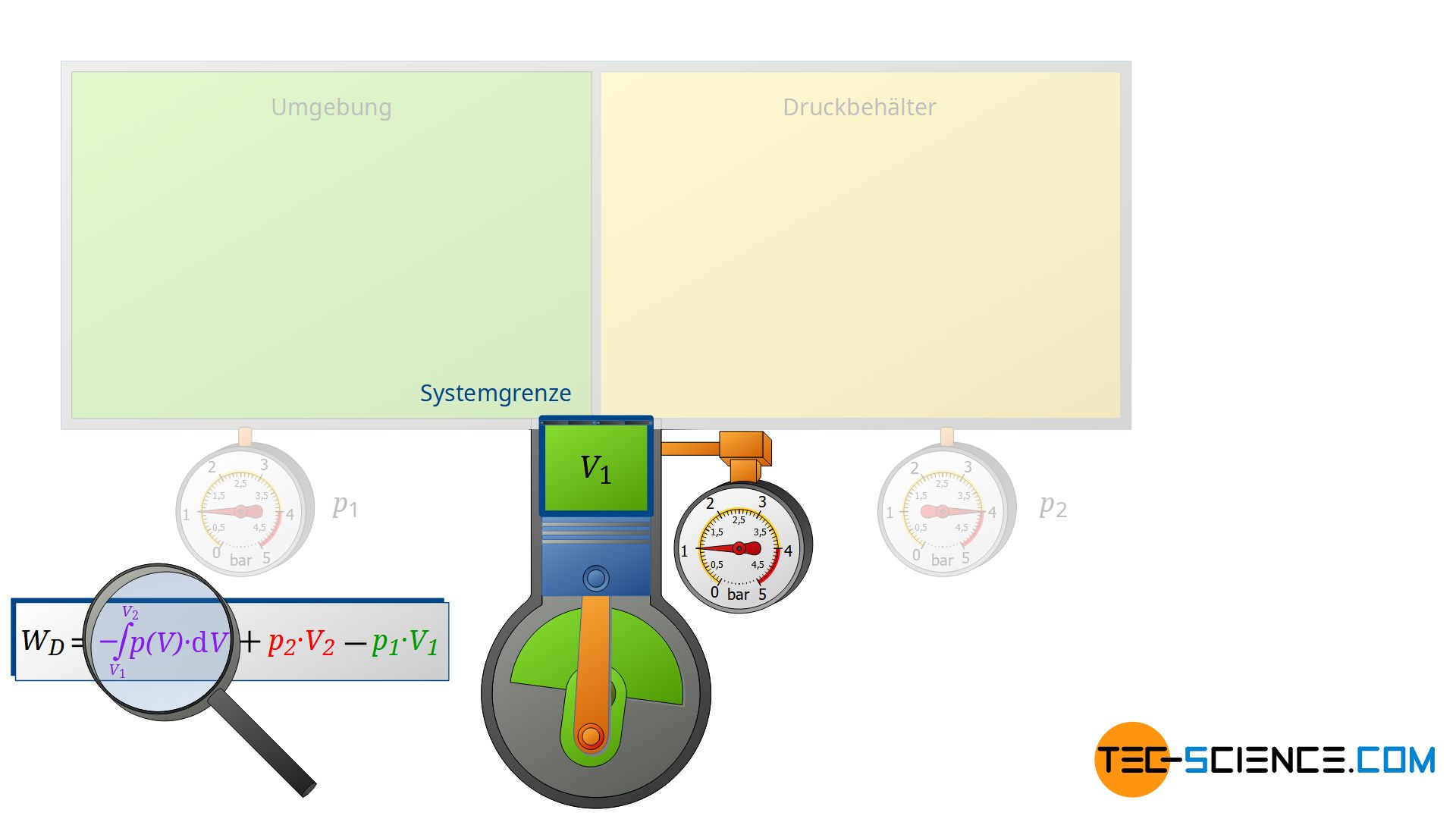
Diese Volumenänderung führt zu einem dritten Arbeitsumsatz W_V, welcher allerdings nicht mehr isobar stattfindet. Deshalb muss für diese Volumenänderungsarbeit im offenen System ganz allgemein das Integral -∫p(V)⋅dV ermittelt werden. Die Summe aller drei Arbeitsumsätze ist vom Verdichter zu erbringen und entspricht der insgesamt vom offenen System umgesetzten Druckänderungsarbeit W_D:

\begin{align}
\label{3568}
W_\text{D} = W_\text{V} +W_2+W_1=-\int\limits_{V_1}^{V_2}p(V)~\text{d}V + p_2~V_2-p_1~V_1
\end{align}

Beachte, dass der Kompressionsvorgang der Luft von V₁ auf V₂ im Verdichter bei geschlossenen Ventilen erfolgt. Somit kann auch dieser Arbeitsumsatz als Volumenänderungsarbeit W_V eines geschlossenen Systems betrachtet werden! Es zeigt sich also, dass sich die einzelnen Terme in Gleichung (\ref{4461}) zur Berechnung der Druckänderungsarbeit stets auf Zustandsänderungen von geschlossenen Systemen zurückführen lassen!

Änderung der Temperatur beim Verdichten

Die isobare Zustandsänderung der Umgebung während dem Einschiebevorgang (Arbeitsumsatz W₁) geht prinzipiell mit einer Temperaturänderung einher. Die Temperaturänderung hängt davon ab, wie stark sich das Volumen der Umgebungsluft ändert. Für ideale Gase gilt hierfür das Gesetz von Gay-Lussac. Es besagt, dass sich bei einem isobaren Prozess die Temperatur im selben Maße ändert wie das Volumen. Die Volumenvergrößerung der Umgebung durch den zurückfahrenden Kolben kann allerdings vernachlässigt werden. Nimmt man bspw. ein Umgebungsvolumen von 50000 Liter an (Raum mit den Maßen 5m x 4m x 2,5m), so würde dieses bei einem Zylindervolumen von V₁=1 l gerade einmal auf ein Endvolumen von 50001 Liter expandiert werden. Die Volumenänderung der Umgebung und damit auch die Temperaturänderung betrüge in diesem Fall gerade einmal 0,002%. Der Einschiebevorgang der Luft in den Verdichter verursacht in der Praxis also keine nennenswerte Temperaturänderung.

Auch die Temperaturänderung der Druckluft im Sammelbehälter während des isobaren Ausschiebeprozesses (Arbeitsumsatz W₂), kann aus den oben genannten Gründen in der Praxis vernachlässigt werden. Denn in der Regel ist auch das Zylindervolumen des Verdichters vernachlässigbar klein gegenüber dem Volumen des Sammelbehälters. Der Ausschiebevorgang der verdichteten Luft in den Druckluftbehälter führt in der Praxis also ebenfalls nicht zu einer nennenswerten Temperaturänderung.

Aber dennoch wird man in der Realität eine deutliche Erhöhung der Temperatur zwischen der eingeschobenen und der ausgeschobenen Luft feststellen! Diese Temperaturänderung kommt allerdings nicht durch den Ein- bzw. Ausschiebevorgang zustande, sondern durch den Kompressionsvorgang im Verdichter selbst (Arbeitsumsatz W_V)! Denn in der Regel erhöht sich bei einer Kompression nicht nur der Druck, sondern auch die Temperatur des Gases. Je nach Verdichterart können dabei Temperaturen von über 100 °C entstehen. Aus diesem Grund werden Verdichter in der Regel gekühlt.

Um die Temperaturänderung während des Verdichtens zu ermitteln, kann der Erste Hauptsatz der Thermodynamik für geschlossene Systeme angewandt werden. Denn wie bereits erläutert, erfolgt der Kompressionsvorgang bei beidseitig geschlossenen Ventilen und somit in einem geschlossenen System. Selbst wenn der Verdichter ohne klassische Ventile arbeitet (z.B. Schraubenverdichter), so kann dieser Vorgang dennoch immer auf ein geschlossenes System zurückgeführt werden. Zum Beispiel dadurch, dass man sich einfach eine Blase um die eingesaugte Luftmasse vorstellt. Z.B. eine „Plastiktüte“ voller Luft, wobei diese selbst die Systemgrenze bildet. Innerhalb dieser Blase ist die Luftmasse konstant und es handelt sich folglich um ein geschlossenes System. Die eingesaugte „Plastiktüte“ voller Luft wird praktisch nur zusammengepresst, ohne dass dabei Masse entweicht noch einströmt.

Der Erste Hauptsatz für ein geschlossenes System besagt nun ganz allgemein, dass die Zufuhr von Arbeit W_V (Volumenänderungsarbeit) und Wärme Q in einer entsprechenden Änderung der inneren Energie ΔU des Stoffes resultieren:

\begin{align}
\label{7560}
\underbrace{-\int\limits_{V_1}^{V_2}p(V)~\text{d}V}_{=W_\text{V}} + Q = \Delta U
\end{align}

Für ein ideales Gas ist die Änderung der inneren Energie ΔU nur auf die Temperaturänderung ΔT zurückzuführen:

\begin{align}
\label{8373}
\Delta U = c_\text{v}~m~\Delta T
\end{align}

Mit einer solchen Betrachtung als ideales Gas kann schließlich aus der zugeführten Volumenänderungsarbeit W_V>0 und der abgeführten Wärme Q<0 durch Kühlung die resultierende Temperaturänderung ΔT bestimmt werden. Oder umgekehrt, kann anhand der Temperaturänderung dann auf die Volumenänderungsarbeit geschlossen werden.