Volumenänderungsarbeit (Volumenarbeit)

Die Volumenänderungsarbeit (Volumenarbeit) entspricht der am Gas oder vom Gas verrichteten Arbeit aufgrund des wirkenden Gasdrucks bei Volumenänderung.

Wärmekraftmaschinen und Wärmepumpen

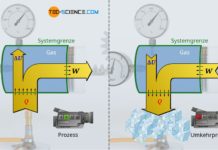
In der Thermodynamik spielen Gase eine wichtige Rolle. Durch sie findet beispielsweise in Verbrennungsmotoren eine Umwandlung von Wärme in Arbeit statt. Aufgrund der entstehende Verbrennungswärme (Zufuhr von Wärme) bei der Verbrennung des Treibstoffs erhöht sich die Temperatur des gasförmigen Treibstoff-Luft-Gemisches. Dies führt zur Druckerhöhung im Zylinder, die den Kolben unten drückt und die Kurbelwelle antreibt (Abgabe von Arbeit). Aus Sicht des Gases wird dem Gas also auf der einen Seite Wärme zugeführt, während dieses wiederum Arbeit nach außen abgibt. Durch das Gas findet also eine Umwandlung von Wärme in Arbeit statt. Man bezeichnet Verbrennungsmotoren deshalb auch ganz allgemein als Wärmekraftmaschinen.

Die umgekehrte Energieumwandlung, d.h. die Umwandlung von Arbeit in Wärme für Heizzwecke, findet hingegen in sogenannten Wärmepumpen statt. Dieses Prinzip einer Wärmepumpe lässt sich anhand einer Luftpumpe verdeutlichen. Verschließt man beim Pumpen das Auslassventil, so steigt nicht nur der Druck sehr stark an, sondern es lässt sich aufgrund der zugeführten Arbeit während der Kompression auch eine Temperaturerhöhung feststellen. Aus Sicht des Gases wird dem Gas also auf der einen Seite Arbeit zugeführt, während dieses wiederum Wärme nach außen abgibt. Durch das Gas findet also eine Umwandlung von Arbeit in Wärme statt.

Gase spielen also sowohl bei Wärmekraftmaschinen, als auch bei Wärmepumpen eine zentrale Rolle. Auf die Abgabe bzw. Aufnahme von Arbeit während der Zustandsänderung eines Gases wird deshalb im Folgenden näher eingegangen. Dies führt schließlich zum Begriff der Volumenänderungsarbeit. Was sich hinter diesem Begriff genau verbirgt und wie sich diese Arbeit in Zustandsdiagrammen anschaulich bestimmen lässt, wird in den nächsten Abschnitten genauer erläutert.

Darstellung von Zustandsänderungen in Volumen-Druck-Diagrammen

Im Folgenden betrachten wir einen horizontal stehenden Zylinder, der reibungsfrei mit einem beweglichen Kolben verschlossen ist. Mit Hilfe der als Zahnstange ausgeführten Kolbenstange wird über ein Zahnrad und ein Hebel ein Gewichtsstück angehoben. Es handelt sich folglich um ein geschlossenes thermodynamisches System mit den Zylinderwänden und der Kolbenfläche als Systemgrenze.

Um das Gewichtsstück anheben zu können, muss der Druck im Zylinder erhöht werden. Dies geschieht durch Wärmezufuhr eines Bunsenbrenners, der die Temperatur des Gases erhöht und somit den Druck ansteigen lässt. Ist der Druck schließlich ausreichend hoch, so beginnt das Gas nun mit bestimmter Kraft die Kolbenstange auszufahren. Dies ist mit einem entsprechenden Aufwand an Arbeit verbunden, den das Gas erbringt, um hierdurch das Gewicht anzuheben.

Betrachten wir nun den Prozess aus Sicht des Gases. Dem Gas wird auf der einen Seite Wärme zugeführt und auf der anderen Seite gibt das Gas Arbeit ab (verrichtet also Arbeit), um den Kolben entgegen der wirkenden Last auszufahren. Während des Anhebens des Gewichtes durchläuft das Gas offensichtlich verschiedene Zustände, die durch unterschiedliche Volumina, Drücke und Temperaturen gekennzeichnet sind. Um solche thermodynamischen Zustandsänderungen des Gases anschaulich abzubilden, werden diese häufig in einem Volumen-Druck-Diagramm dargestellt. Für den vorlegenden Fall stellt sich der Prozess aus Sicht des Gases wie abgebildet dar.

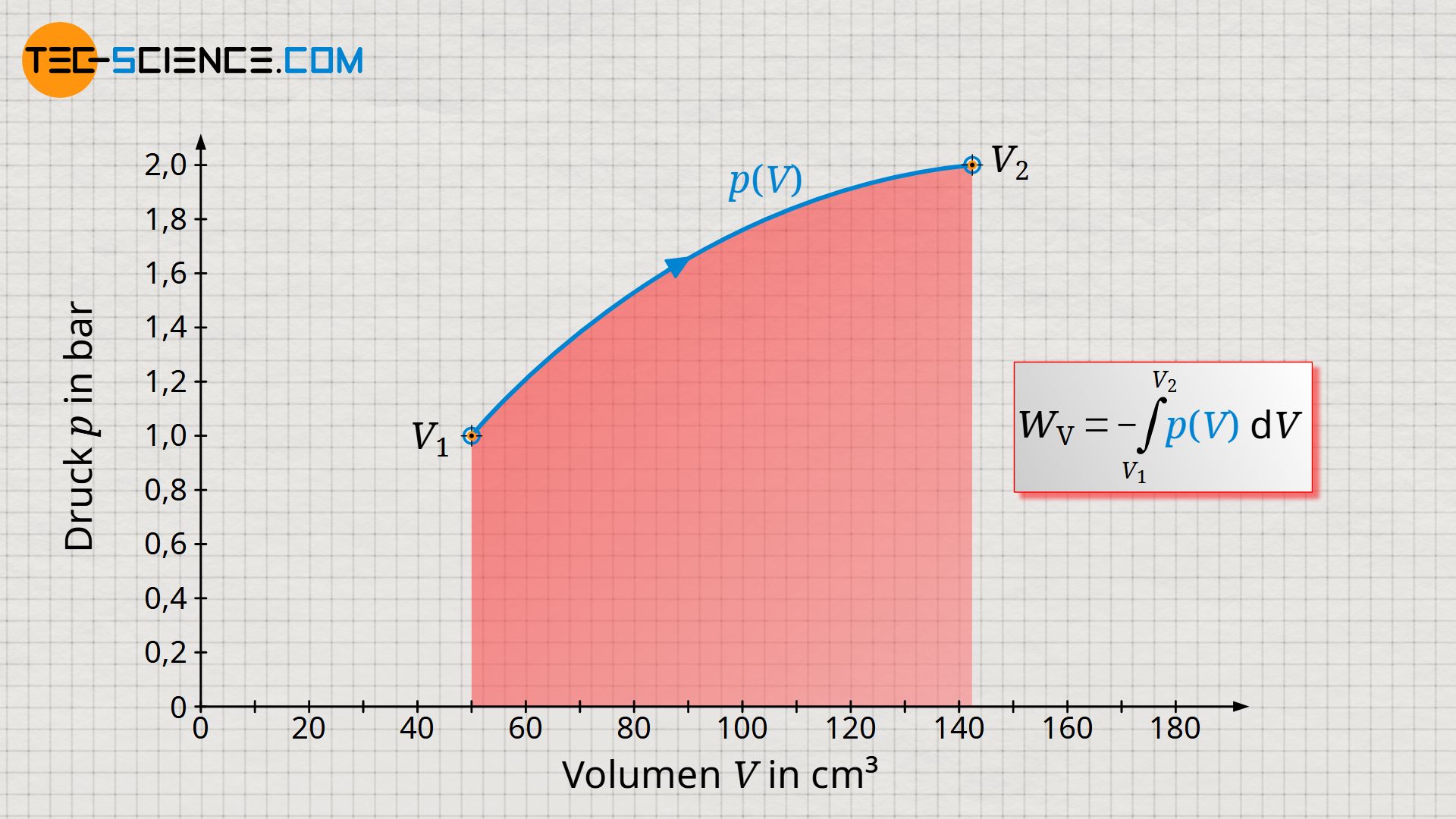
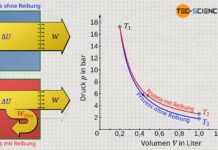
Zur Erläuterung des Druckverlaufs: Zu Beginn des Prozesses steht der Gasdruck mit dem Luftdruck von 1 bar im Gleichgewicht, sodass also auch das im Zylinder befindliche Gas einen Druck von 1 bar aufweist. Das Gas besitzt in diesem Ausgangszustand ein Volumen von 50 ml, wobei die Temperatur 20 °C beträgt. Aufgrund der Wärmezufuhr und den damit verbundenen Temperaturanstieg erhöht sich nun der Druck. Gleichzeitig hat dies zur Folge, dass der Kolben hierdurch bewegt wird und das Gewicht angehoben wird. Das Gasvolumen vergrößert sich dabei. Aufgrund des größer werdenden Hebelverhältnisses beim Anheben muss das Gas in der Folge immer mehr Kraft aufbringen um das Gewicht weiter anheben zu können. Der Gasdruck muss bei weiterer Volumenvergrößerung folglich stetig zunehmen. Schließlich ist das Gewicht bei einem Gasvolumen von 142,5 ml vollständig angehoben. Der Druck beträgt in diesem Endzustand rund 2 bar bei einer Gastemperatur von 1413 °C.

In einem Volumen-Druck-Diagramm kann nicht nur der Prozessablauf abgebildet werden, sondern es bietet auch die vom Gas verrichtete Arbeit anschaulich zu ermitteln. Diese Arbeit ergibt sich als Fläche unter der Zustandskurve! Dies zeigt auch ein kurzer Vergleich der Einheiten, die auf den Achsen aufgetragen sind und bei einer Flächenberechnung entsprechend miteinander zu multiplizieren sind:

\begin{align}
&\text{[Fläche]} = [p] \cdot [V] = \frac{\text{N}}{\text{m²}} \cdot \text{m³} = \text{N} \cdot \text{m} = \text{J} = \text{[Arbeit]}   \\[5px]
\end{align}

Eine Fläche unter der Zustandskurve und damit ein Arbeitsumsatz kann sich natürlich nur dann ergeben, wenn sich bei einer Zustandsänderung das Gasvolumen ändert. Deshalb bezeichnet man die vom Gas bzw. am Gas verrichtete Arbeit auch als Volumenänderungsarbeit W_V (kurz: Volumenarbeit). Mathematisch lässt sich diese Volumenänderungsarbeit als Integral der Druckfunktion p(V) innerhalb der Grenzen zwischen Anfangsvolumen V₁ und Endvolumen V₂ bestimmen (eine ausführliche Herleitung der folgenden Formel findet sich im Artikel Herleitung der Volumenänderungsarbeit wieder.):

\begin{align}
\boxed{W_\text{V} = – \int\limits_{V_1}^{V_2} p(V) ~ \text{d}V} ~~~\text{Volumenänderungsarbeit}  \\[5px]
\end{align}

Beachte, dass die Volumenänderungsarbeit bei einer Expansion (Volumenvergrößerung) vom Gas verrichtet wird, d.h. das Gas gibt dabei Arbeit über die Systemgrenze nach außen ab. Wohingegen bei einer Kompression (Volumenverkleinerung) die Volumenänderungsarbeit am Gas verrichtet wird, d.h. dem Gas wird über die Systemgrenze hinweg Arbeit zugeführt.

Die Volumenänderungsarbeit (Volumenarbeit) entspricht der am Gas oder vom Gas verrichteten Arbeit aufgrund des wirkenden Gasdrucks bei Volumenänderung.

Volumenarbeit als Prozessgröße

Ist bei einem thermodynamischen Prozess der Anfangs- und der Endzustand des Gases bekannt, so ist es für die Ermittlung der Volumenänderungsarbeit zwangsweise nötig zu wissen, wie der Prozess genau abläuft. Denn je nach Prozessführung können sich unter Umständen gänzlich unterschiedliche Flächen unter den Zustandskurven und somit unterschiedliche Volumenänderungsarbeiten ergeben.

Im Vergleich zum oben beschriebenen Anhebeprozess mittels Zahnstangenmechanismus sind zwei weitere thermodynamische Prozesse im p(V)-Diagramm abgebildet. Obwohl Anfangs- und Endzustände offensichtlich identisch sind, ergeben sich jedoch unterschiedliche Flächen unter den Kurven und somit verschiedene Beträge für die Volumenarbeit. Im Vergleich zum Ausgangsprozess (1) ist die Volumenänderungsarbeit in der zweiten Variante (2) geringer und in der dritten Prozessführung (3) größer. Dementsprechend kann das Gewicht im Fall (2) nicht so weit angehoben werden wie in der ersten Variante. In der Variante (3) hingegen kann das Gewicht durch die größere Volumenänderungsarbeit auch um einen entsprechend größeren Betrag angehoben werden.

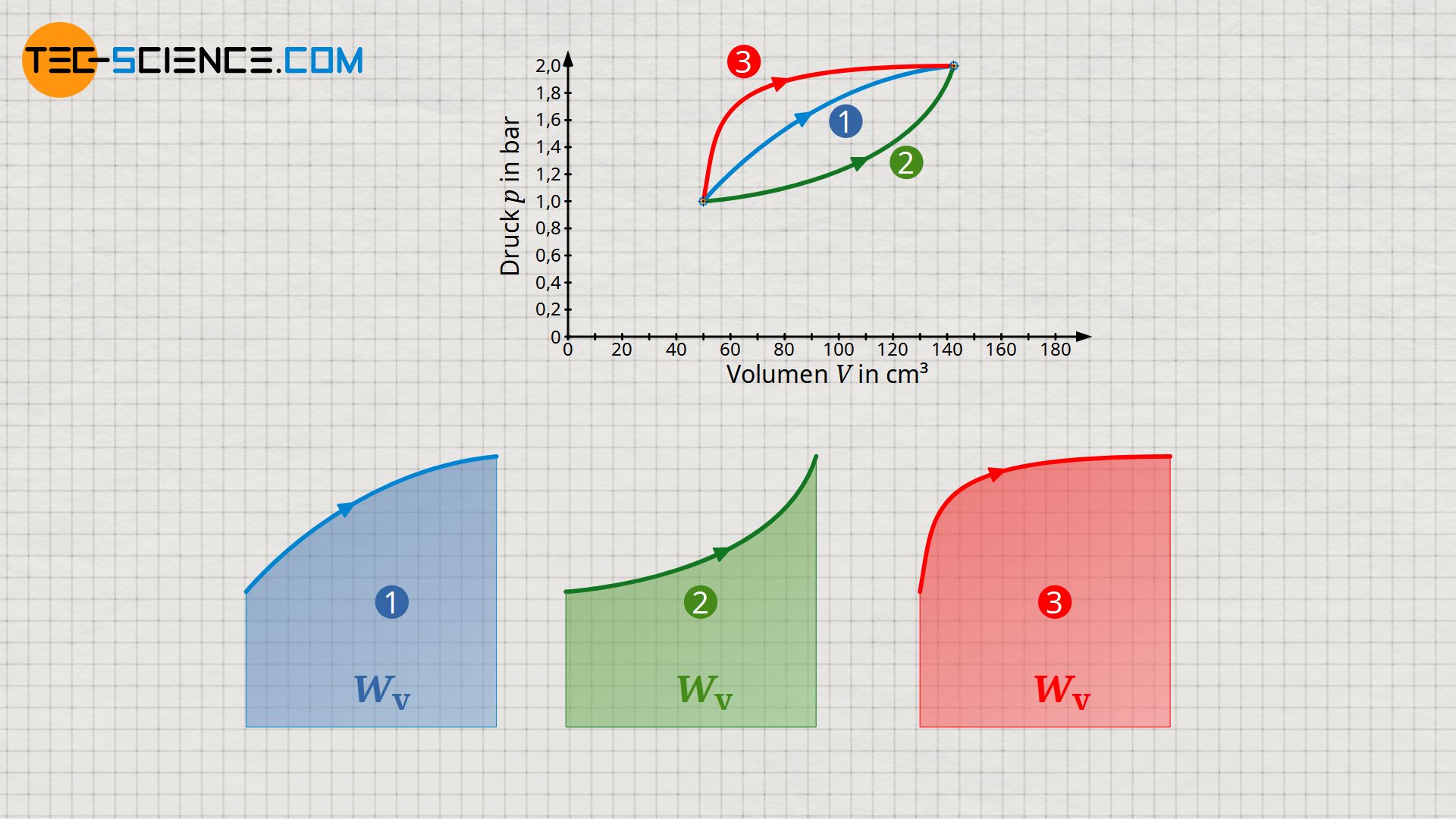
Die Volumenänderungsarbeit hängt somit im entscheidenden Maße davon ab, wie der Prozess zwischen dem Anfangs- und Endzustand genau verläuft. Es handelt sich bei der Volumenänderungsarbeit eben um eine typische Prozessgröße. Weitere Informationen hierzu finden sich auch im Artikel Die Prozessgrößen: Wärme und Arbeit.

Die Volumenänderungsarbeit ist eine Prozessgröße und ergibt sich im Volumen-Druck-Diagramm als Fläche unterhalb der Zustandskurve (wegabhängig)!

Volumenarbeit ≠ Nutzarbeit

Man könnte nun vorschnell meinen, dass die Volumenänderungsarbeit des Gases auch der Arbeit entspricht, die das System am Gewicht in Form von Hubarbeit verrichtet. Im Allgemeinen ist dies allerdings aus zweierlei Sicht nicht der Fall!

Zum einen muss bedacht werden, dass das Gas den Kolben nicht nur aufgrund der angehängten Last verschieben muss (Hubarbeit), sondern auch entgegen des äußeren Luftdrucks außerhalb des Zylinders, der von der Gegenseite her auf den Kolben wirkt (Verschiebearbeit). Die am Gewicht verrichtete Hubarbeit entspricht letztlich dem Nutzen, der mit der gesamten Apparatur bezweckt wird und wird deshalb auch als Nutzarbeit bezeichnet, während das Verschieben des Kolbens entgegen des äußeren Luftdrucks Verschiebearbeit genannt wird.

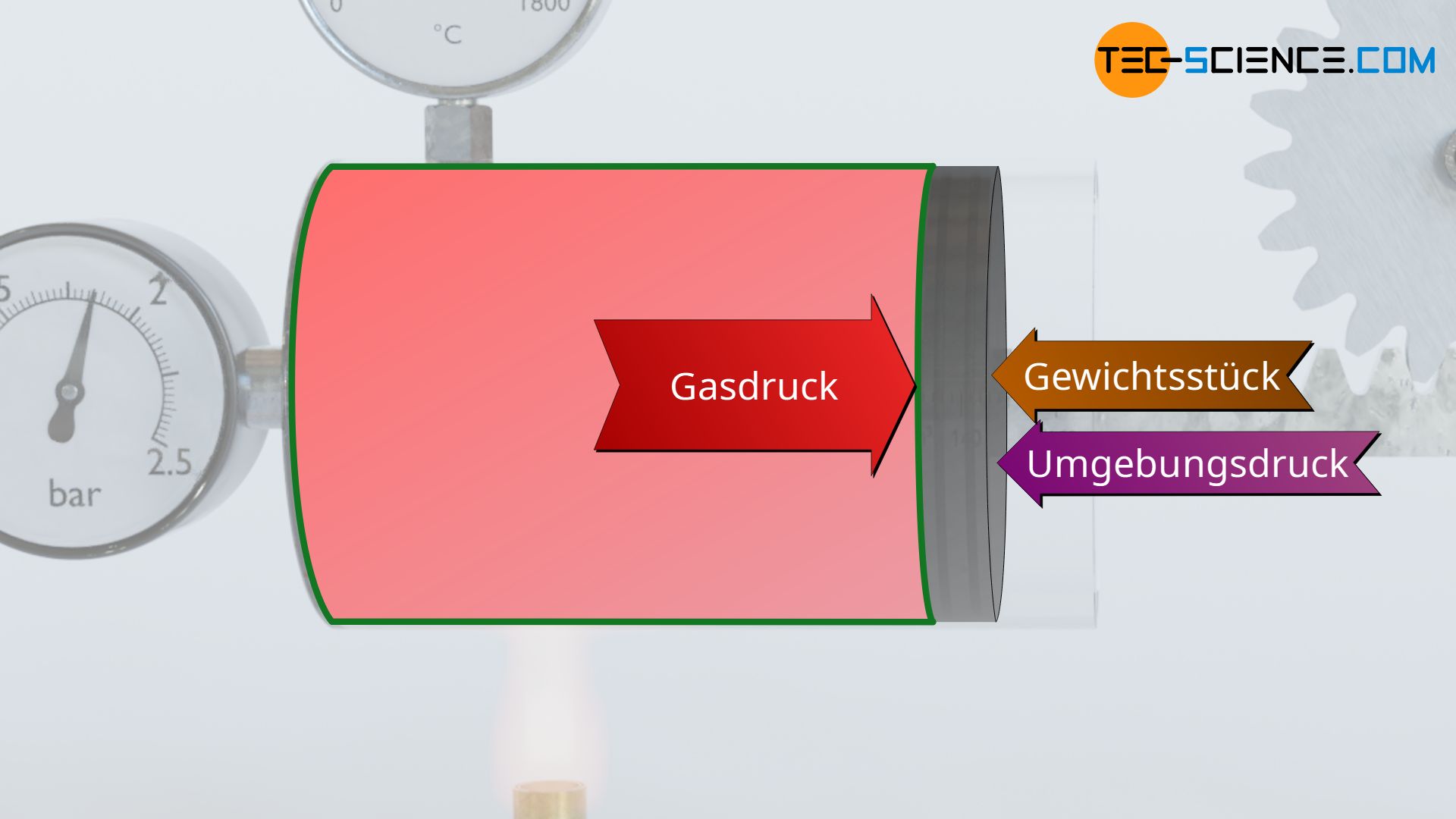
Zum anderen muss beachtet werden, dass Prozesse in der Realität nicht reibungsfrei ablaufen. Im vorliegenden kommt zwischen Kolben und Zylinderwand zu Reibungseffekten. Das Gas muss den Kolben somit auch entgegen der wirkenden Reibung verschieben. Das Gas verrichtet deshalb zusätzlich noch Reibungsarbeit. Diese Reibungsarbeit wird oft auch als Dissipationsarbeit bezeichnet. Auf die Dissipation von Energie wird in einem separaten Artikel näher eingegangen.

Die Volumenarbeit W_V, die das Gas zur Vergrößerung seines Volumens verrichten muss (Fläche unter der p(V)-Zustandskurve!), ergibt sich im Allgemeinen folglich aus der Summe von Nutzarbeit W_N, Verschiebearbeit W_S und Reibungsarbeit W_R:

\begin{align}
\boxed{W_\text{V} = W_\text{N} + W_\text{S} + W_\text{R} }  \\[5px]
\end{align}

Erster Hauptsatz der Thermodynamik

Gibt das Gas bei der oben beschriebenen Energieumwandlung die gesamte zugeführte Wärmeenergie Q wieder in Form von mechanischer Arbeit W nach außen ab?

Um diese Frage zu beantworten, betrachten wir die Situation unmittelbar nach dem vollständigen Anheben der Last. Dabei wird deutlich, dass das Gas offensichtlich nur dann in der Lage ist das Gewicht in Stellung zu halten, wenn der Gasdruck entsprechend hoch ist, um die notwendige Haltekraft zu erzeugen. Dieser erforderliche Gasdruck wird durch eine starke Temperaturzunahme erzielt. Die Temperatur des Gases muss also nach dem Anheben des Gewichtes zwangsweise höher sein als zu Beginn. Dies wiederum bedeutet allerdings eine Änderung der inneren Energie des Gases, die für ein ideales Gas direkt mit der Temperaturänderung verknüpft ist. In diesem konkreten Fall eine Zunahme der inneren Energie.

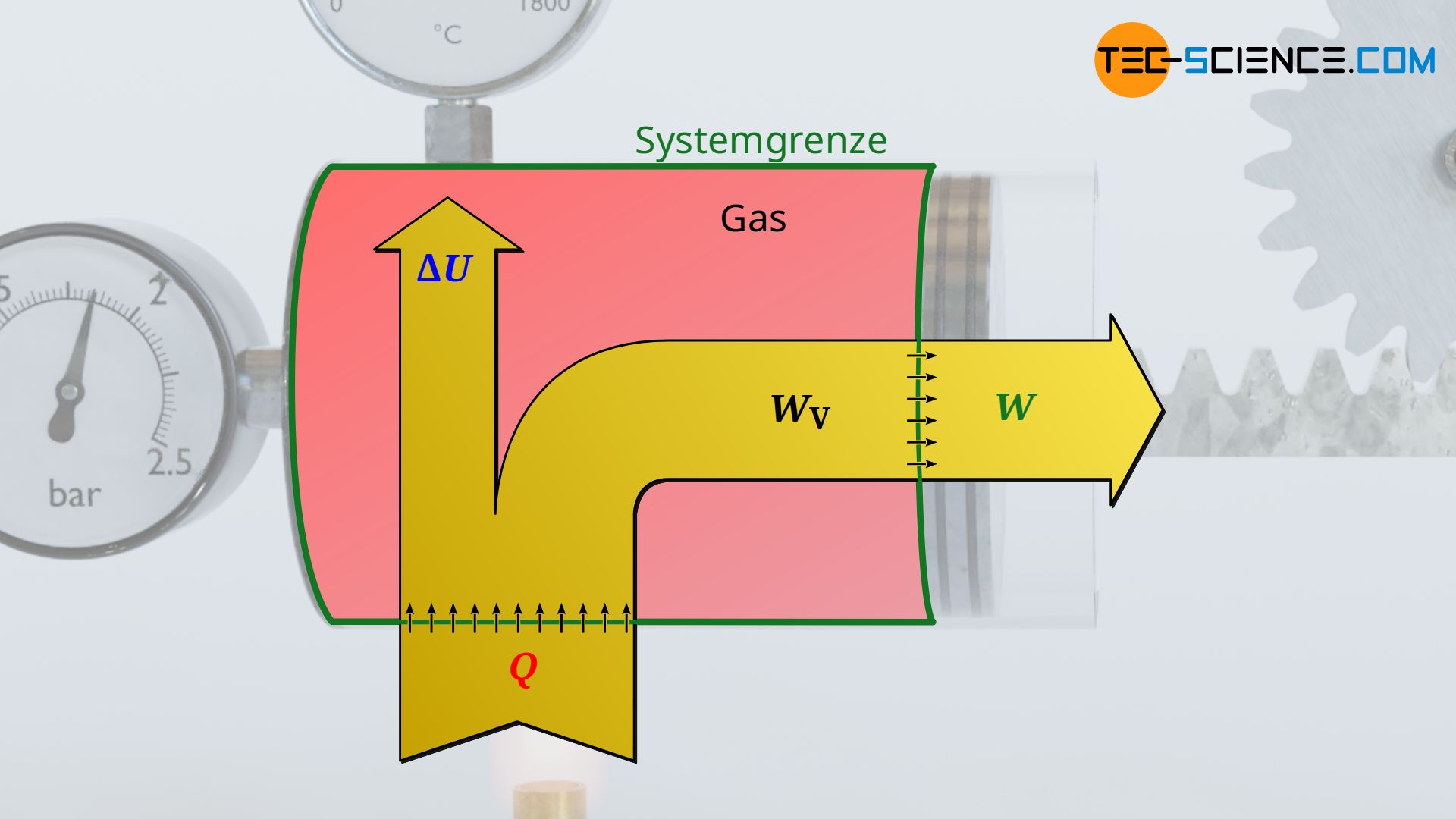
Die Energiezufuhr durch Wärme Q>0 wird also nicht wieder vollständig in Form von Arbeit W<0 nach außen abgegeben. Ein gewisser Teil der zugeführten Wärmeenergie verbleit als innere Energie ΔU>0 im System und sorgt für die notwendige Temperaturerhöhung (zur Vorzeichenkonvention siehe Artikel Innere Energie & Erster Hauptsatz der Thermodynamik)! Die entsprechende Bilanzierung der Energien wird im Ersten Hauptsatz der Thermodynamik beschrieben. Für das vorliegende geschlossene System stellt sich dieser wie folgt dar:

\begin{align}
\label{wg}
&\boxed{W + Q = \Delta U} ~~~\text{Erster Hauptsatz für geschlossene Systeme}\\[5px]
\end{align}

Beachte, dass die im ersten Hauptsatz aufgeführte Wärme Q und Arbeit W stets als Energieumsätze zu verstehen sind, die über die Systemgrenze des geschlossenen Systems hinweg transportiert werden (Prozessgrößen!). Diese bewirken im Inneren eine entsprechende Änderung der inneren Energie ΔU des Gases (Zustandsgröße!). Für einen reibungsfreien Fall, d.h. ohne Dissipation von Energie, entspricht die über die Systemgrenze hinweg transportierte Arbeit W gerade der Volumenänderungsarbeit W_V des Gases.