Die Van-der-Waals-Gleichung beschreibt den Zusammenhang zwischen Druck, Volumen und Temperatur für reale Gase.
Ideale Gasgleichung (Gasgesetz für ideale Gase)
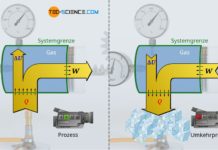
In thermodynamischen Prozessen werden Gase der Einfachheit halber häufig als ideale Gase betrachtet. Je nachdem welche Menge eines Gases in einem bestimmten Volumen eingeschlossen wird, erzeugt dieses Gas in Abhängigkeit der Temperatur einen bestimmten Druck. Der Zusammenhang zwischen Gasmasse m, Gasvolumen V, Temperatur T und hieraus resultierendem Druck p wird durch die sogenannte ideale Gasgleichung beschrieben (darin bezeichnet Rm die allgemeine Gaskonstante, die unabhängig der Gasart ist):
\begin{align}
\label{ideal}
&\boxed{p \cdot V = n \cdot R_\text{m} \cdot T} ~~~~~\text{ideale Gasgleichung}\\[5px]
\end{align}
Bei der Betrachtung der Gase als ideale Gase wurde die Annahme zugrunde gelegt, dass die Gasteilchen als Punktmassen anzunehmen sind, d.h. keine Ausdehnung besitzen. Die Teilchen in realen Gasen besitzen aber ein Eigenvolumen, das berücksichtigt werden muss. Des Weiteren wird in der Modellvorstellung von idealen Gasen davon ausgegangen, dass keinerlei Anziehungskräfte zwischen den Teilchen wirken. In der Realität beeinflussen sich die Gasteilen durch ihre gegenseitige Anziehungskraft allerdings gegenseitig.
Sowohl die Berücksichtigung des Eigenvolumens der Gasteilchen als auch die gegenseitige Wechselwirkung machen eine Modifikation der idealen Gasgleichung nötig, wenn es um die Beschreibung von realen Gasen geht. Dies mündet schließlich in der sogenannten Van-der-Waals-Gleichung, die im Folgenden näher beschrieben wird.
Berücksichtigung der Anziehungskraft der Teilchen
Betrachtet wird nun ein reales Gas, das sich in einem geschlossenen Behälter befindet. Die Gasmoleküle untereinander üben eine geringe Anziehungskraft aufeinander auf. In hinreichend großem Abstand zur Wand sind die Gasteilchen allerdings „umringt“ von Nachbarteilchen. Da im zeitlichen Mittel die Anziehungskraft, die die Teilchen ausüben symmetrisch in alle Richtungen verläuft, erfährt ein solches Teilchen keine resultierende Kraft. Dieselbe Argumentation gilt natürlich für jedes andere Teilchen auch, solange sich dieses nicht in der Nähe der Wand befindet.
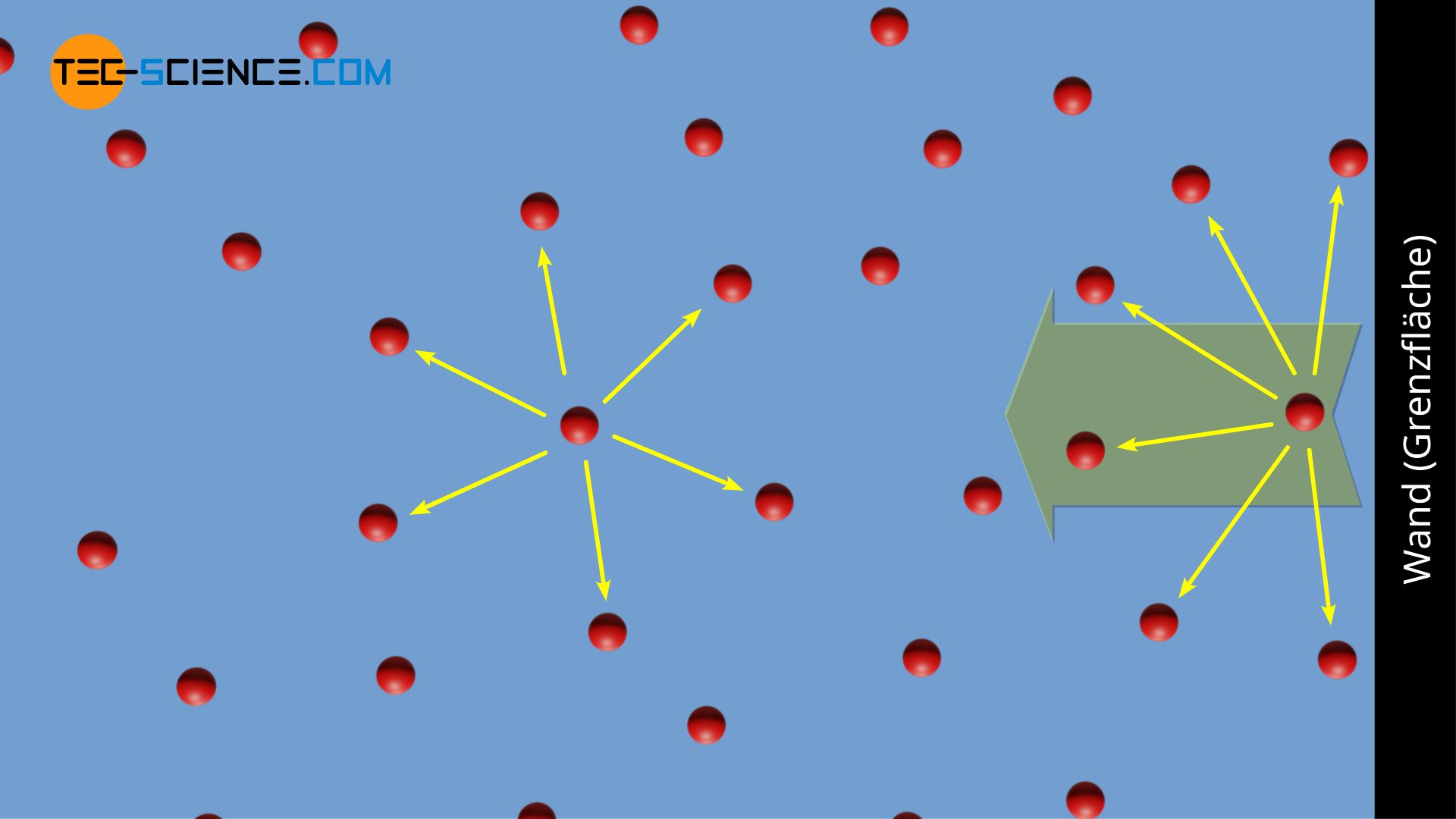
Anders sieht die Situation allerdings aus, wenn sich ein Gasteilchen in der Nähe der Wand aufhält. Für ein solches Teilchen befinden sich fernab der Wand mehr Teilchen. Damit verspürt dieses eine resultierende Kraft, welche von der Wand weggerichtet ist. Fliegt also ein Gasteilchen auf die Gefäßwand zu, so wird dieses durch die resultierende Kraft etwas abgebremst. Der Impulsübertrag beim Stoß mit der Wand ist hierdurch reduziert. Dieser Impulsübertrag macht allerdings den messbaren Druck in einem Gas aus (siehe Artikel Druck in Gasen), welcher durch die unmittelbar zuvor stattgefundene Abbremsung der Teilchen reduziert wurde.
Unter Berücksichtigung der gegenseitigen Anziehungskraft der Teilchen, ist also der reale messbare Druck p in einem Gas um einen Betrag Δp geringer als wenn das Gas als ideales Gas betrachtet werden würde (Druck pideal):
bzw.
\begin{align}
\label{pi}
& p < p_\text{ideal} ~~~\Rightarrow~~~ \underline{p_\text{ideal} = p + \Delta p} \\[5px]
\end{align}
Der Effekt, dass für ein ideales Gas der Druck pideal um einen Betrag Δp größer ist als wenn dieses Gas als reales Gas betrachtet werden würde (Druck p) ist im Wesentlichen von der Teilchendichte n/V bestimmt (mit n als Stoffmenge). Dieser Druckunterschied Δp, wird auch Binnendruck oder Kohäsionsdruck genannt. Dabei zeigt sich, dass dieser Binnendruck Δp proportional zum Quadrat der Teilchendichte (n/V)² ist:
\begin{align}
\label{dp}
& \Delta p \sim \left(\frac{n}{V}\right)^2 ~~~\Rightarrow~~~ \boxed{\Delta p = a \cdot \left(\frac{n}{V}\right)^2} ~\text{Binnendruck}\\[5px]
\end{align}
Zur quantitativen Beschreibung des Binnendrucks wurde in der oberen Gleichung ein Proportionalitätsfaktor a eingeführt, der letztlich vom verwendeten Gas abhängig ist und aus empirischen Untersuchungen bestimmt wird. Insgesamt kann also festgehalten werden, dass sich der Druck eines als ideal betrachteten Gases pideal um den Wert a⋅(n/V)² höher liegt als der Druck des realen (tatsächlichen) Gases. Wird Gleichung (\ref{dp}) in Gleichung (\ref{pi}) eingesetzt, so zeigt sich offensichtlich folgender Zusammenhang zwischen dem idealen Gasdruck und dem realen Gasdruck:
\begin{align}
\label{pp}
& \boxed{p_\text{ideal} = p + a \cdot \left(\frac{n}{V}\right)^2} \\[5px]
\end{align}
Berücksichtigung des Eigenvolumens der Teilchen
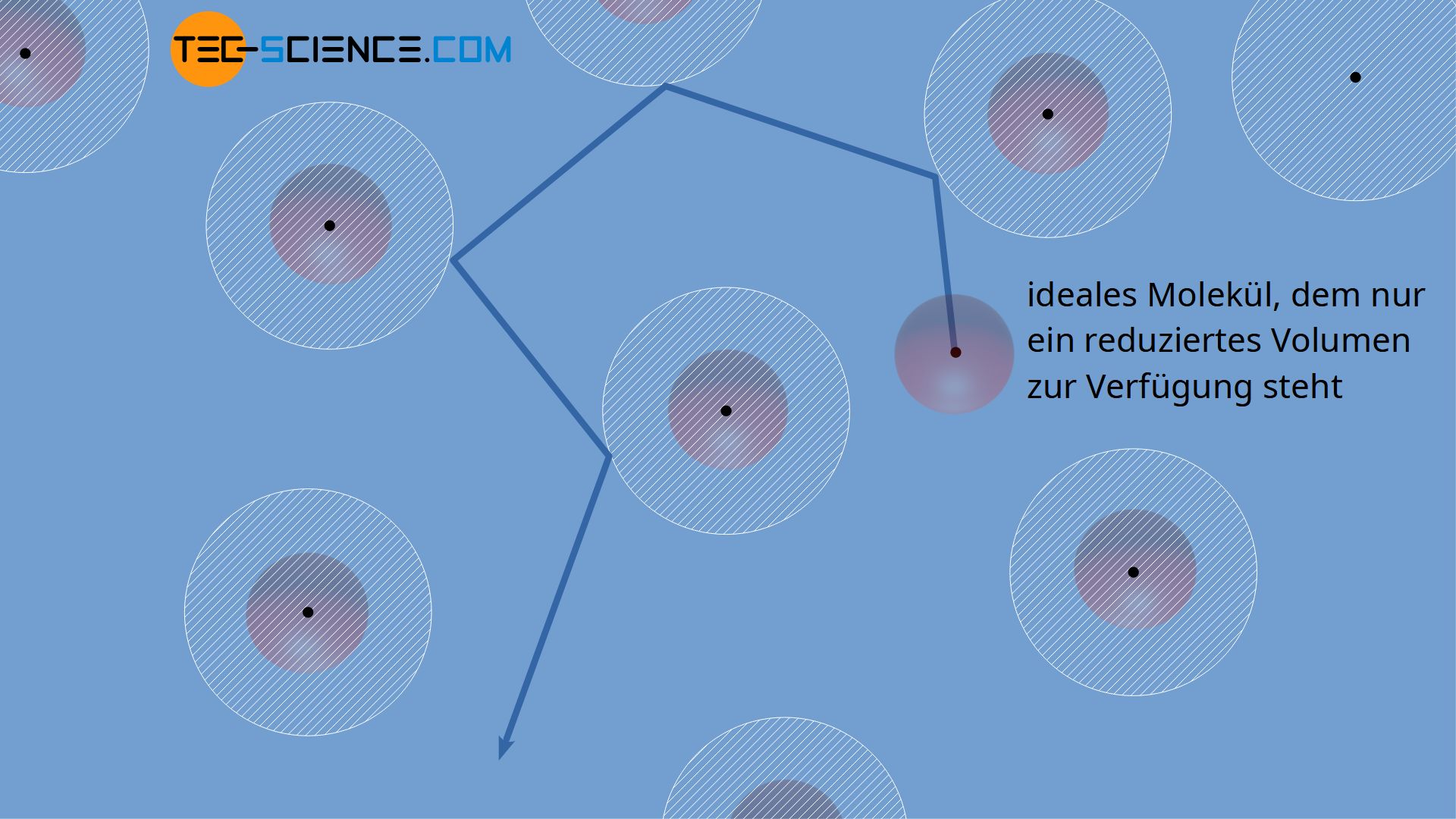
Für ein ideales Gas, dessen Teilchen als (verschwindend kleine) Massepunkte angenommen werden können, steht im Prinzip das gesamte Gasvolumen V für deren Bewegung zur Verfügen. Für reale Gase muss jedoch das Eigenvolumen der Teilchen mitberücksichtigt werden. Es steht den einzelnen Gasteilchen damit effektiv weniger freies Volumen für deren Bewegung zur Verfügung.
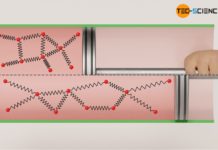
Der Massenmittelpunkt eines Teilchens kann sich offensichtlich nur bis auf einen minimalen Abstand der Wand nähern, der gerade dem Teilchenradius des realen Gasmoleküls entspricht. Die in der Abbildung weiß schraffierte Zone stellt deshalb eine „verbotene“ Zone dar, in die die Teilchen nicht eindringen können. Damit verringert sich das effektiv für die Bewegung der Teilchen zur Verfügung stehende Volumen.
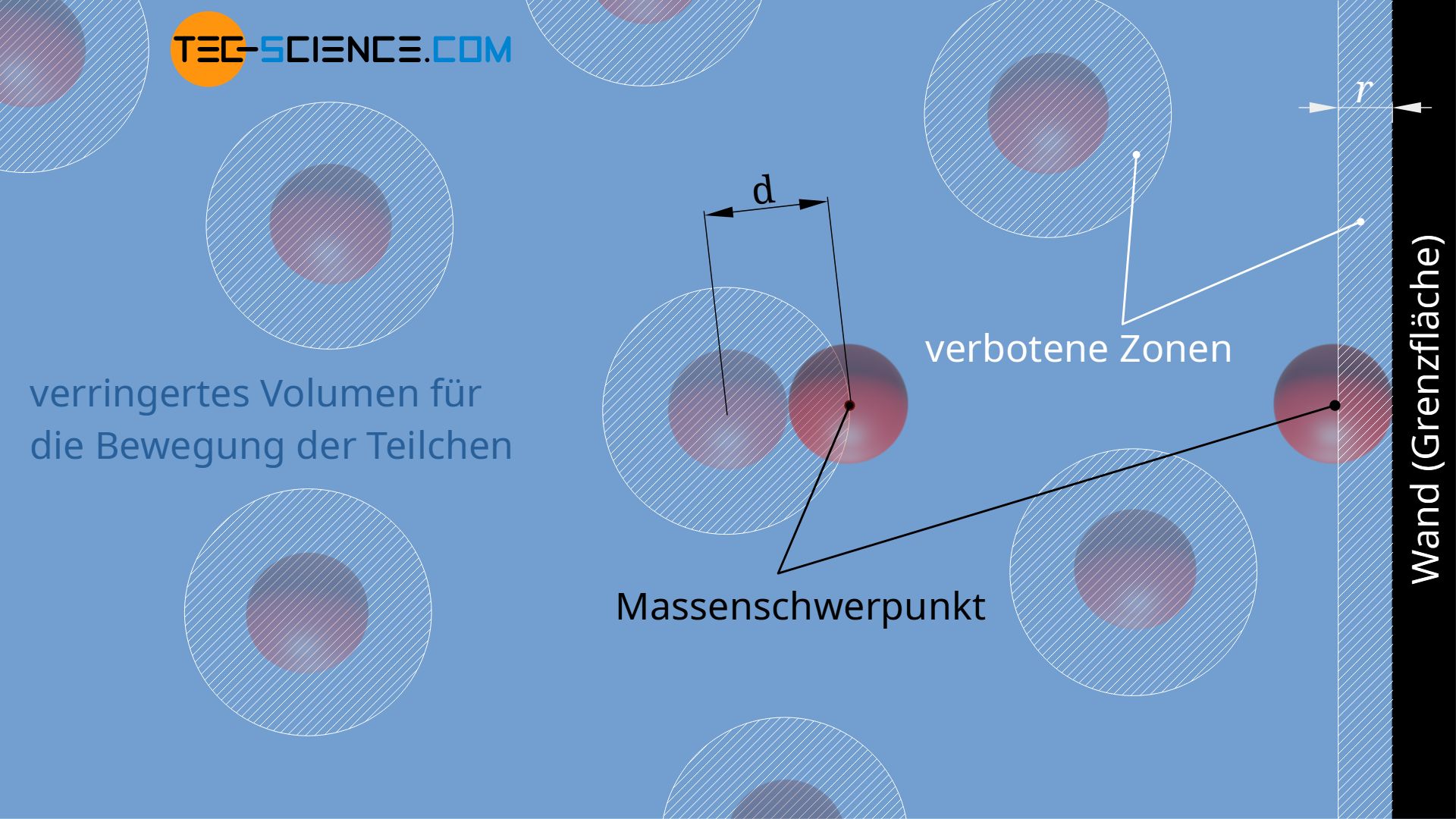
Aber nicht nur in der Nähe der Gefäßwand, sondern auch um die Teilchen selbst bilden sich verbotene Bereiche. So können sich die Massenschwerpunkte zweier Teilchen maximal bis auf den Teilchendurchmesser d nähern. Unterschreitet ein Teilchen diesen Abstand, dann käme es zu einem Stoß. Den Teilchen steht für die Bewegung somit ein geringes Volumen zur Verfügung als geometrisch vorhanden. Das effektive Bewegungsvolumen der Teilchen wird damit zusätzlich eingeschränkt.
Wird das geometrisch vorhandene Volumen mit V und die Reduktion des Volumen aufgrund der verbotenen Zonen mit ΔV bezeichnet, so ergibt sich das effektive Gasvolumen Veff, innerhalb dessen sich die Teilchen frei bewegen können, wie folgt:
\begin{align}
\label{ve}
& V_\text{eff} = V – \Delta V \\[5px]
\end{align}
Das verbotene Volumen durch die Wandzone kann gegenüber den verbotenen Bereichen, die sich um die Teilchen herum ergeben, vernachlässigt werden. Deshalb ist der Volumenverlust ΔV nur durch die verbotenen Bereiche der Gasteilchen bestimmt. Umso mehr Teilchen sich also in einem Gas befinden, desto größer werden die nicht zugänglichen Bereich, d.h. das verbotene Volumen V ist proportional zur Stoffmenge n:
\begin{align}
\label{dv}
& \Delta V \sim n ~~~\text{bzw.}~~~ \boxed{\Delta V = b \cdot n} ~\text{Kovolumen („Eigenvolumen“ der Teilchen)} \\[5px]
\end{align}
Auch an dieser stelle wurde zur quantitativen Beschreibung des effektiven Volumens wieder eine Proportionalitätskonstante b eingeführt, die von der verwendeten Gasart abhängig und empirisch zu ermitteln ist. Wird Gleichung (\ref{dv}) in Gleichung (\ref{ve}) eingesetzt, so zeigt sich offensichtlich folgender Zusammenhang zwischen dem geometrischen Volumen und dem effektiv zur Verfügung stehendem Volumen:
\begin{align}
\label{veff}
& \boxed{V_\text{eff}= V – b \cdot n} \\[5px]
\end{align}
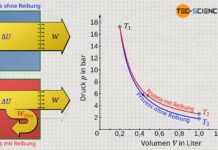
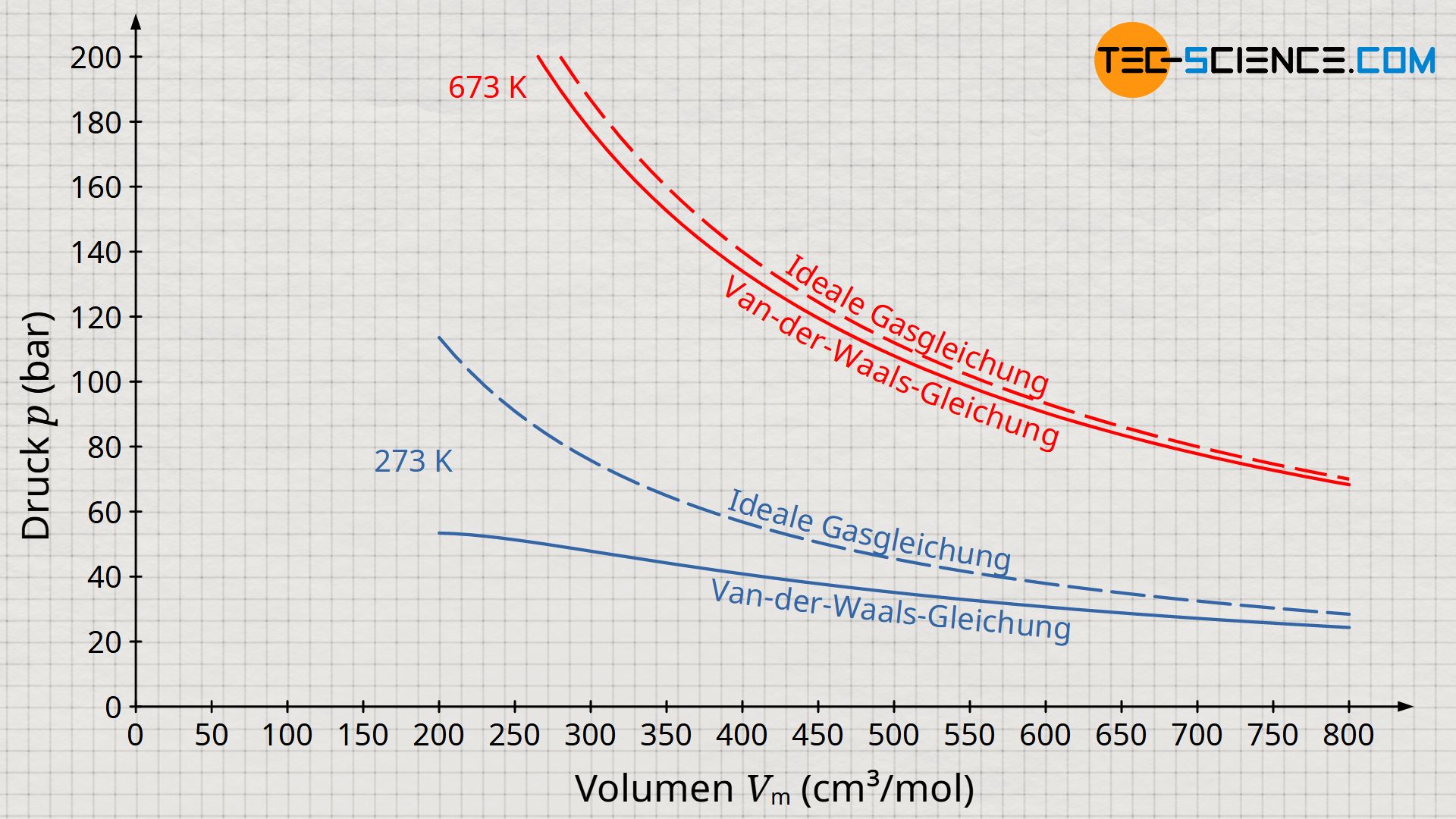
Die Verkleinerung des effektiven Volumens hat auf den Druck den gegenteiligen Effekt wie die Berücksichtigung der Anziehungskraft zwischen den Teilchen. Eine Verkleinerung des zur Verfügung stehenden Volumens entspräche bei einem idealen Gas letztlich einer Kompression, welcher zur Erhöhung des Drucks führt. Anders als die Berücksichtigung der gegenseitigen Anziehungskraft zwischen den Gasteilchen, führt die Berücksichtigung des Eigenvolumens der Gasmoleküle deshalb zur Erhöhung des Druck bei realen Gasen im Vergleich zu idealen Gasen. Beide Effekte heben sich allerdings nicht gegenseitig auf, da beide Effekte anderen Gesetzmäßigkeiten folgen (siehe Volumen-Druck-Diagramm unten)!
Van-der-Waals-Gleichung
An dieser Stelle kann man nun die ideale Gasgleichung (\ref{ideal}) verwenden, um sowohl das Kovolumen als auch den Binnendruck zu berücksichtigen. In einem ersten Schritt wird zunächst berücksichtigt, dass bei einem realen Gas offensichtlich nicht mehr das gesamte geometrische Gasvolumen für die Gasteilchen zur Verfügung steht, sondern lediglich das effektive Volumen Veff. Die ideale Gasgleichung gestalt sich somit wie folgt:
\begin{align}
&\color{red}{p_\text{ideal}} \cdot \color{blue}{V_\text{eff}} = n \cdot R_\text{m} \cdot T \\[5px]
\end{align}
In einem zweiten Schritt setzten wir nun die für das reale Gas geltenden Zusammenhänge gemäß Gleichung (\ref{pp}) und Gleichung (\ref{veff}) ein:
\begin{align}
&\boxed{\color{red}{\left[p+a \cdot \left(\frac{n}{V}\right)^2\right]} \cdot \color{blue}{\left(V- b \cdot n \right)} = n \cdot R_\text{m} \cdot T} ~~~\text{Van-der-Waals-Gleichung} \\[5px]
\end{align}
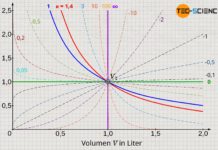
Diese Gleichung wird schließlich Van-Der-Waals-Gleichung genannt und beschreibt das Verhalten von realen Gasen unter Berücksichtigung des Eigenvolumens und der gegenseitige Wechselwirkung der Gasteilchen. Beachte, dass unter Vernachlässigung des Binnendrucks (a=0) und des Kovolumens (b=0) die Van-der-Waals-Gleichung in die ideale Gasgleichung übergeht. Auch für hohe Temperaturen bzw. geringer Drücke nähert sich die Van-der-Waals-Gleichung mehr und mehr der idealen Gasgleichung an.
Die Van-der-Waals-Gleichung ist eine Modifikation der idealen Gasgleichung und berücksichtigt sowohl das Eigenvolumen der Gasteilchen als auch die untereinander wirkenden Anziehungskräfte!
Die Van-der-Waals-Gleichung lässt sich auch mit Hilfe des molaren Volumens Vm=V/n, als Quotient von geometrischem Volumen V und Stoffmenge n, ausdrücken:
\begin{align}
&\boxed{\color{red}{\left(p+\frac{a}{V_\text{m}^2}\right)} \cdot \color{blue}{\left(V_\text{m} – b\right)} = R_\text{m} \cdot T} ~~~\text{mit}~~~\boxed{V_\text{m}=\frac{V}{n}}~~\text{molares Volumen} \\[5px]
\end{align}
Die untere Tabelle gibt für verschiedene Gase den experimentell ermittelten Binnendruck a und das Kovolumen b für ausgewählte reale Gase wieder. Beachte, dass diese Größen im allgemeinen keine Konstanten sind, sondern vom Druck und von der Temperatur abhängig sind. Sie stellen also lediglich Näherungswerte dar. Vor allem bei hohen Drücken, bei denen die Gasteilchen auf ein sehr geringes Volumen gepresst werden, gibt es starke Abweichungen zu den unten angegebenen Konstanten bzw. die Van-der-Waals-Gleichung liefert keine brauchbaren Ergebnisse mehr.
Für den Fall, dass bspw. der Druck so groß wird und damit das molare Volumen Vm kleiner wird als das Kovolumen b, versagt die Van-der-Waals-Gleichung offensichtlich, da die linke Seite der Gleichung dann negativ wird; die rechte Seite aber stets positiv bleibt. Untersuchungen zeigen aber, dass das molare Volumen von realen Gasen durchaus kleiner als das angegebene Kovolumen sein kann, da es sich bei den Gasmolekülen ja nicht wie angenommen um starre Kugeln handelt, die bei vollständigem aneinanderschmiegen nicht mehr weiter zusammengepresst werden können.
| Gasart | Binnendruck a in 10-3 J⋅m³/mol² | Kovolumen b in 10-6 m³/mol |
|---|---|---|
| Ammoniak (NH3) | 424 | 37 |
| Argon (Ar) | 136 | 32 |
| Chlor (Cl2) | 655 | 56 |
| Helium (He) | 3,45 | 24 |
| Kohlendioxid (CO2) | 365 | 43 |
| Luft | 136 | 37 |
| Methan (CH4) | 230 | 43 |
| Neon (Ne) | 21 | 17 |
| Propan (C3H8) | 93 | 90 |
| Sauerstoff (O2) | 138 | 32 |
| Stickstoff (N2) | 141 | 39 |
| Wasser (H2O) | 553 | 30 |
| Wasserstoff (H2) | 25 | 27 |
Mit Hilfe der Van-der-Waals-Gleichungen lassen sich nicht nur präzisiere Aussagen zum Verhalten von realen Gasen machen, sondern diese Gleichung liefert auch eine Erklärung, warum sich Gase bei hohen Drücken verflüssigen. Im Artikel Erklärung der Verflüssigung von Gasen (Van-der-Waals-Gleichung) wird hierauf näher eingegangen.