Erfahre in diesem Artikel mehr über polytrope thermodynamische Prozesse in geschlossenen Systemen.
Ausgewählte Prozesse im Volumen-Druck-Diagramm
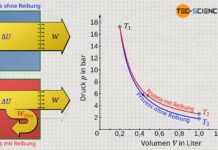
Die untere Abbildung zeigt den Verlauf des Drucks in Abhängigkeit des Volumens für einen isobaren, isochoren, isothermen und isentropen Prozess. Alle Prozesse finden dabei ausgehend des Anfangsvolumens V1 statt. Die Druckverläufe zeigen sowohl einen Expansionsvorgang als auch einen Kompressionsvorgang. Für die isentrope Zustandsänderung wurde der Isentropenexponent von Luft mit κ=1,4 gewählt.
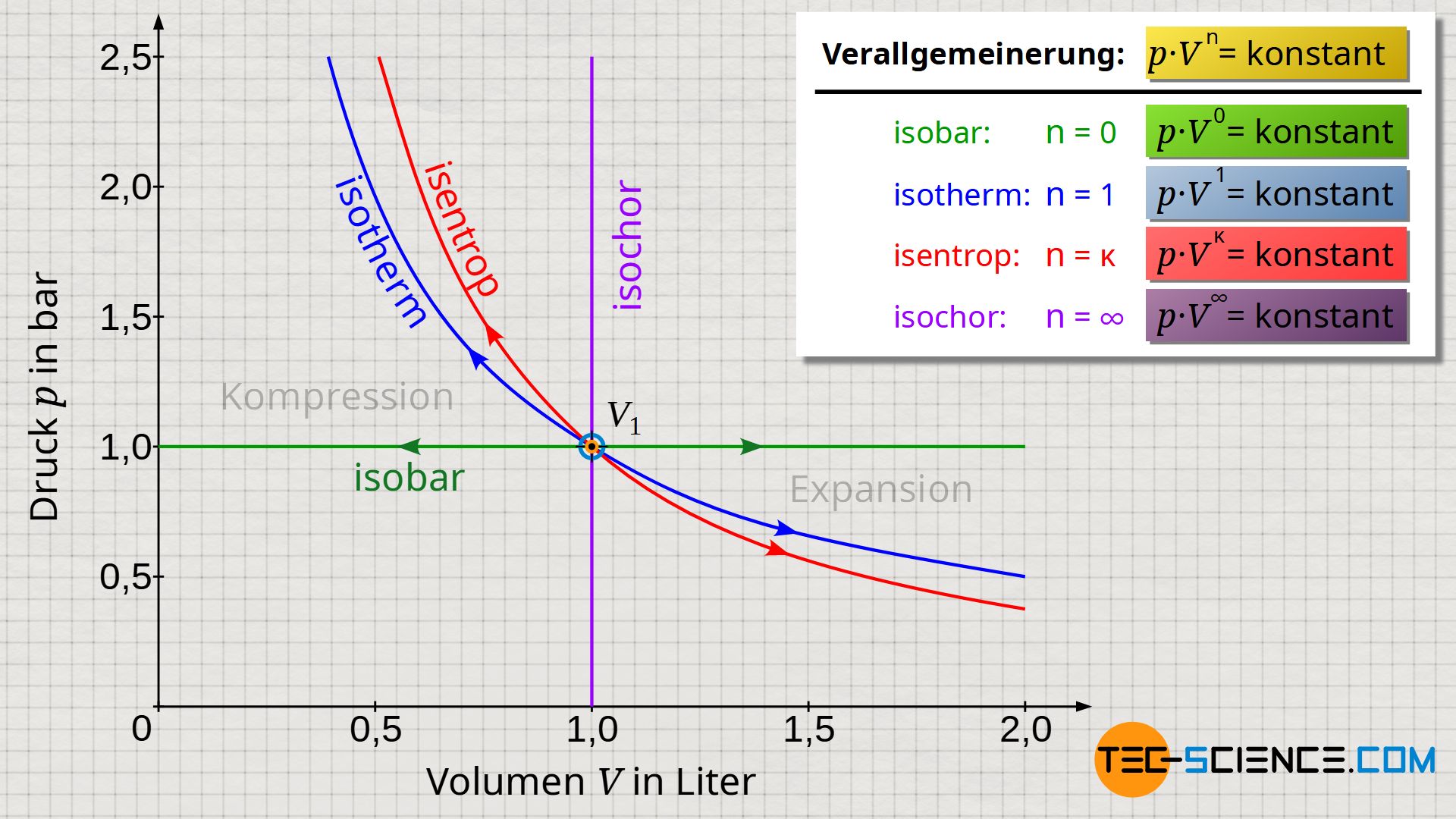
Obwohl sich die unterschiedlichen thermodynamischen Prozesse auf den ersten Blick stark voneinander unterscheiden, so stellt man bei näherer Untersuchung Gemeinsamkeiten fest. Diese werden deutlich, wenn man die qualitativen Verläufe des Druckes in Abhängigkeit des Volumens näher betrachtet:
\begin{alignat}{3}
\text{isobarer Prozess: } ~~~ &p=\text{konstant} &&~~~~~~ \Rightarrow ~~~ &&& { p~V^0 =\text{konstant}} \\[5px]
\text{isothermer Prozess: } ~~~ &p\sim {1\over V} &&~~~~~~ \Rightarrow ~~~ &&& { p~V^1 =\text{konstant}} \\[5px]
\text{isentroper Prozess: } ~~~ &p\sim {1\over V^{\kappa}} &&~~~~~~ \Rightarrow ~~~ &&& { p~V^{\kappa} =\text{konstant}} \\[5px]
\text{isochorer Prozess: } ~~~ &V=\text{konstant} &&~~~~~~ \Rightarrow ~~~ &&& { p~V^{\infty} =\text{konstant}} \\[5px]
\label{8858}
\end{alignat}
Aus der Gegenüberstellung wird deutlich, dass sich die gesamten dargestellten Prozesse auf den Zusammenhang p⋅Vn=konstant verallgemeinern lassen, wobei sich für jeden Prozess ein ganz spezieller Exponent n finden lässt:
\begin{align}
\label{3445}
\text{Verallgemeinerung: } ~~~ & \boxed{p~V^{n} =\text{konstant}} ~~~\text{ bzw. }~~~ {p_1~V_1^n}={p_2~V_2^n} \\[5px]
\end{align}
Anmerkung: Weshalb für den isochoren Prozess n=∞ gilt, wird rasch deutlich, wenn man Gleichung (\ref{3445}) nach dem Volumen V umstellt und anschließend n=∞ setzt:
\begin{align}
p~V^n=\text{konst.} ~~~\Rightarrow ~~~
V ={\left(\text{konst.} \over p \right)^{1 \over n}}
={\text{konst.} \over p^{1 \over n}}
\overset{n=\infty}={\text{konst.} \over \underbrace{p^0}_{=1}}
=\text{konstant!} \nonumber \\[5px]
\end{align}
Verallgemeinerung der Zustandsgleichungen
Sowohl für den Zusammenhang zwischen Temperatur und Volumen als auch zwischen Temperatur und Druck zeigen sich die analogen Gemeinsamkeiten der Prozesse. Diese Gemeinsamkeiten können durch Verknüpfung der idealen Gasgleichung mit der Grundgleichung (\ref{3445}) hergeleitet werden. Somit lassen sich alle bisher behandelten Prozesse auf folgende (gemeinsame) Gesetzmäßigkeiten reduzieren:
\begin{align}
\label{2716}
\boxed{p~V^n=\text{konstant}} &~~\Rightarrow~~ \boxed{p_1~V_1^n=p_2~V_2^n} \\[5px]
\label{4375}
\boxed{T~V^{n-1}=\text{konstant}} &~~\Rightarrow~~ \boxed{T_1~V_1^{n-1}=T_2~V_2^{n-1}} \\[5px]
\label{7991}
\boxed{T^n~p^{1-n}=\text{konstant}} &~~\Rightarrow~~ \boxed{T_1^n~p_1^{1-n}=T_2^n~p_2^{1-n}} \\[5px]
\text{ mit: }~~ &n=0 ~~~\text{für isobraren Prozess} \nonumber \\
&n=1 ~~~\text{für isothermen Prozess} \nonumber \\
&n=\kappa ~~~\text{für isentropen Prozess} \nonumber \\
&n=\infty ~~~\text{für isochoren Prozess} \nonumber \\
\end{align}
Der Exponent n bleibt jedoch nicht auf die Spezialfälle (isobar, isotherm, isentrop und isotherm) beschränkt. Grundsätzlich kann der Exponent beliebig gewählt werden! Die Wahl hängt im entscheidenden Maße davon ab, durch welchen Wert des Exponenten die in der Realität ablaufende Zustandsänderung am besten beschrieben werden kann. Schließlich laufen die meisten thermodynamischen Prozesse in der Realität nie exakt isobar, isotherm, isentrop oder isochor ab. Das unten abgebildete Diagramm zeigt für beliebige Werte von n die zugehörigen Druckverläufe. Je nachdem welche Kurve dem tatsächlichen Prozess am nächsten kommt, wäre dann der entsprechende Exponent zu wählen. Prinzipiell sind auch negative Exponenten denkbar!
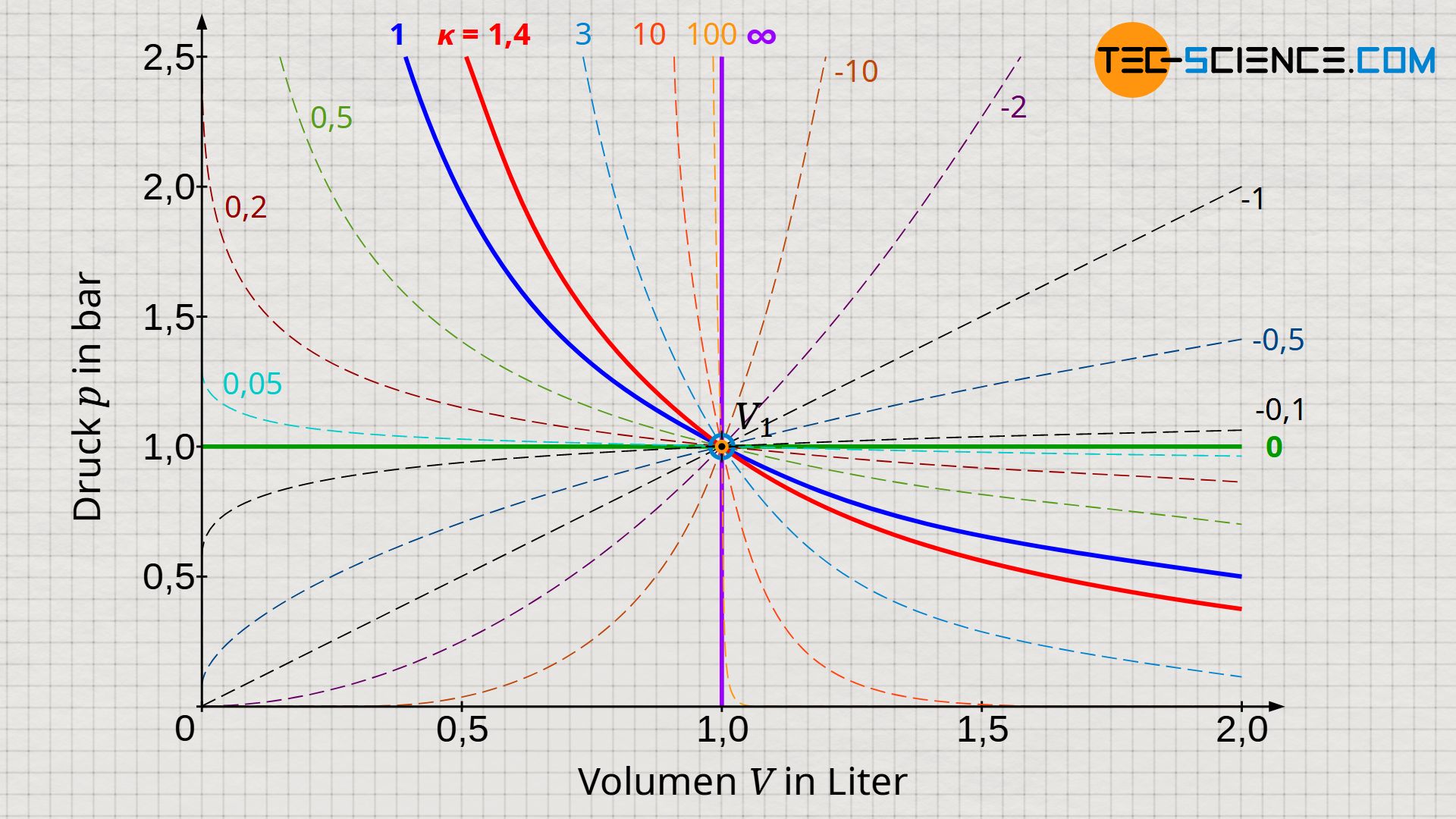
Beachte, dass letztlich die gesamten abgebildeten Kurven alle zur selben Kurvenschar gehören, die durch die Gleichung (\ref{2716}) beschrieben werden.
Da mit den Gleichung (\ref{2716}) bis (\ref{7991}) eine Vielzahl an thermodynamischen Vorgängen beschrieben werden können (die Spezialfälle eingeschlossen), bezeichnet man die dahinterstehenden Prozesse auch ganz allgemein als polytrope Prozesse („poly“=viel). Der Exponent n wird deshalb auch Polytropenexponent genannt. Die isobaren, isothermen, isentropen und isochoren Prozesse sind demnach lediglich als Spezialfälle eines im Allgemeinen polytropen Prozesses anzusehen!
Volumenänderungsarbeit und Wärmeumsatz
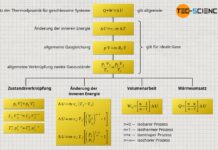
Neben der Beschreibung der Zustandsgrößen durch die Gleichungen (\ref{2716}) bis (\ref{7991}), lassen sich für polytrope Prozesse auch allgemeingültige Formeln zu den Prozessgrößen wie Volumenänderungsarbeit WV und Wärmeumsatz Q finden, sowie zur Änderung der inneren Energie ΔU. Auf die Herleitung der nachfolgend angegebenen Formeln wird aufgrund der Komplexität im verlinkten Artikel näher eingegangen. In diesem Artikel sollen die Formeln lediglich vorgestellt und diskutiert werden.
\begin{alignat}{2}
\label{4862}
&\boxed{W_\text{V} = \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~\left(T_2-T_1 \right)}& &= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[\left(T_2\over T_1\right)-1 \right] \\[5px]
&&&= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[20px]
\label{5451}
&\boxed{Q = \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~\left(T_2-T_1 \right)}& &= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[\left(T_2\over T_1\right)-1 \right] \\[5px]
&&&= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[20px]
\label{9277}
&\boxed{\Delta U = c_\text{v}~m~\left(T_2-T_1 \right)}& &= c_\text{v}~m~T_1~\left[{T_2 \over T_1}-1 \right] \\[5px]
&&&= c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&=c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[5px]
\end{alignat}
Beachte, dass der Isentropenexponent κ in den oberen Gleichungen lediglich als Quotient der Wärmekapazitäten aufzufassen ist (κ=cp/cv). Man sollte also nicht dem Trugschluss verfallen, dass die oberen Gleichungen lediglich für den isentropen Prozess gelten, nur weil sich der Isentropenexponent κ verbirgt! Grundsätzlich können diese Gleichungen für jeden beliebigen, polytropen Prozess angewendet werden, die Spezialfälle natürlich eingeschlossen!
Aufgepasst werden muss an dieser Stelle jedoch für den Spezialfall des isothermen Prozesses mit einem Polytropenexponenten von n=1, da hierbei der Nenner in den Gleichungen null werden würde. Mathematisch betrachtet, ergibt sich hierfür dann keine Lösung. Für diesen Fall müssen die speziellen Gleichungen für den isothermen Prozess benutzt werden. Mit hinreichender Genauigkeit kann als Alternative jedoch ein Polytropenexponent nahe Eins gewählt werden, zum Beispiel n=0,999.
Zusammenhang zwischen Änderung der inneren Energie und Volumenarbeit bzw. Wärme
Betrachtet man die Gleichungen (\ref{4862}) und (\ref{5451}) genauer, so fällt auf, dass der darin enthaltene Term cv⋅m⋅(T2-T1) letztlich der Änderung der inneren Energie ΔU entspricht. Somit kann die Volumenänderungsarbeit WV und der Wärmeumsatz Q auch in Abhängigkeit der Änderung der inneren Energie ΔU angegeben werden:
\begin{align}
\label{6763}
&\boxed{W_V= \left[{{\kappa-1} \over {n-1}}\right] ~\Delta U} \\[5px]
&\boxed{Q= \left[{{n-\kappa} \over {n-1}}\right] ~\Delta U} \\[5px]
\end{align}
Es wird nun offensichtlich, dass der Arbeit- und Wärmeumsatz für einen gegebenen polytropen Prozess stets in einem konstanten Verhältnis stehen:
\begin{align}
\require{cancel}
\label{3657}
{W_V \over Q} = {{\left[{{\kappa-1} \over \bcancel{n-1}}\right]~\bcancel{\Delta U}} \over {\left[{{n-\kappa} \over \bcancel{n-1}}\right]~\bcancel{\Delta U}}}
= { {\kappa-1} \over {n-\kappa} } \\[5px]
\end{align}
\begin{align}
\label{3285}
\boxed{{ W_V \over Q } = { {\kappa-1} \over {n-\kappa} }} \\[5px]
\end{align}
Das untere Diagramm zeigt für Luft (κ=1,4) den Betrag des Verhältnisses von Volumenänderungsarbeit zu Wärmeumsatz in Abhängigkeit des Polytropenexponenten.
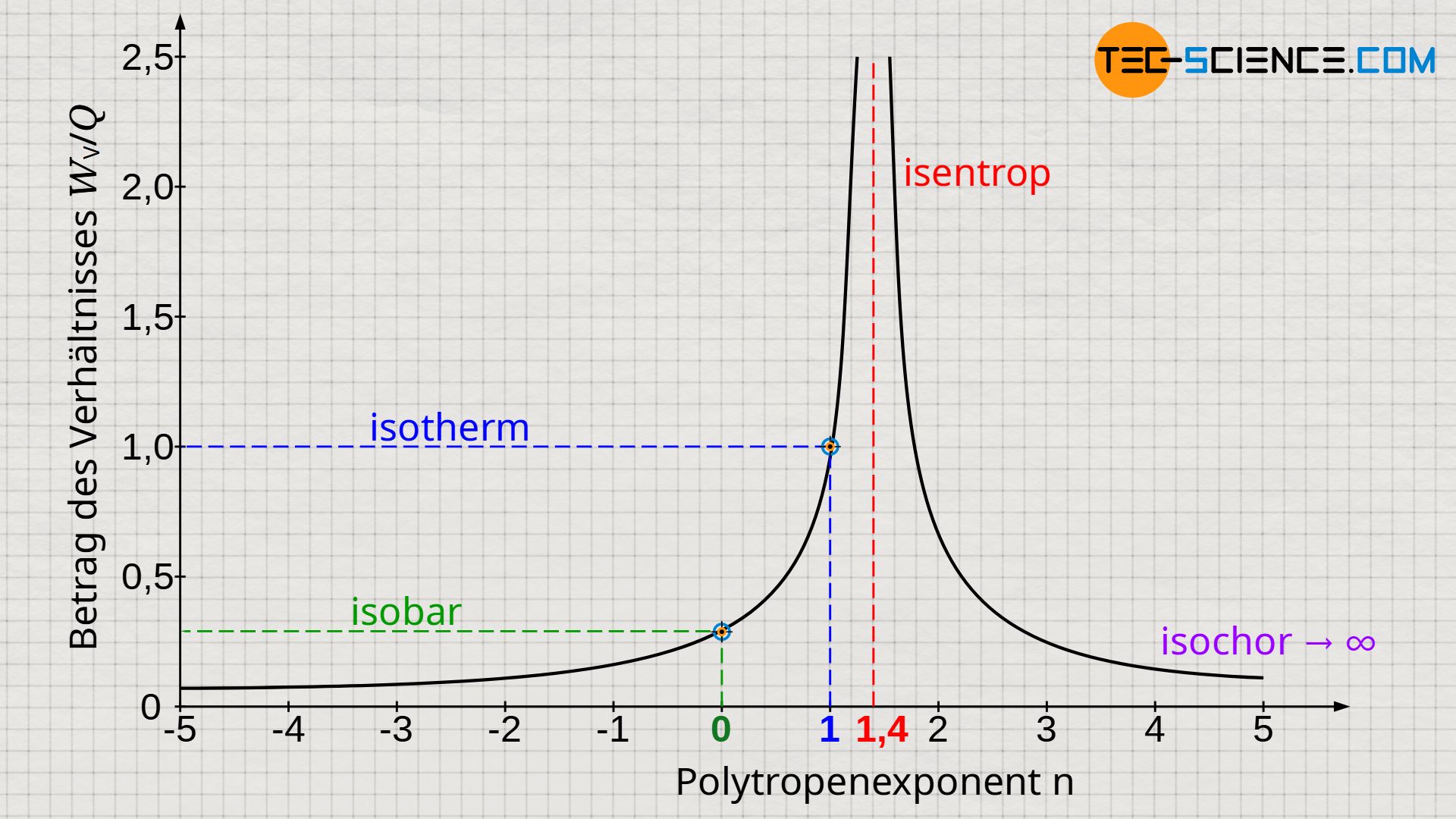
Isobarer Prozess
Für jeden isobaren Prozess mit n=0 und κ=1,4 (für Luft), beträgt das Verhältnis von Arbeit zur Wärme (-)0,286. Für eine isobare Expansion wird folglich immer 28,6% der zugeführten Wärme in Volumenänderungsarbeit umgewandelt. Die restlichen 71,4% verbleiben im Gas und führen zur Erhöhung der inneren Energie. Dieses Ergebnis ist unabhängig davon mit welchem Druck, Volumen oder mit welcher Temperatur die isobare Zustandsänderung abläuft! Lediglich die Gasart hat je nach Wert des Isentropenexponenten Einfluss auf die Effektivität, mit der die zugeführte Wärme in Arbeit umgewandelt wird. So lässt sich bspw. der Anteil der Volumenänderungsarbeit auf 40,1% steigern, wenn für die isobare Expansion anstelle der Luft hingegen Helium mit einem Wert von κ=1,67 als Gas genutzt wird!
Isentroper Prozess
Für einen thermodynamischen Prozess der mit einem Polytropenexponent n<κ beschrieben wird, wird die Gleichung (\ref{3285}) negativ. Dies bedeutet, dass Volumenänderungsarbeit und Wärmeumsatz offensichtlich entgegengesetzte Vorzeichen besitzen. Somit muss dem Gas während einer Expansion (WV<0) Wärme zugeführt werden (Q>0). Umgekehrt muss bei solchen Prozessen Wärme abgeführt werden (Q<0), wenn das Gas komprimiert wird (WV>0).
Für eine Zustandsänderung, die hingegen mit einem Polytropenexponent n>κ beschrieben wird, ist das Verhältnis von Arbeit und Wärme positiv. Beide Energieumsätze haben demzufolge identische Vorzeichen. Dies bedeutet, dass das Gas während einer Expansion (WV<0) Wärme abgibt (Q<0). Umgekehrt findet bei solchen Zustandsänderungen eine Wärmezufuhr statt (Q>0), wenn sich das Gasvolumen unter Zufuhr von Arbeit verringert (WV>0).
Für den Sonderfall eines Prozesses mit einem Isentropenexponenten n→κ nähert sich der Nenner in der Gleichung (\ref{3285}) immer mehr dem Wert null. Folglich nimmt der Wärmeumsatz (bezogen auf die Volumenänderungsarbeit) ab und ist bei n=κ schließlich null. Man erhält für diesen Spezialfall den isentropen Prozess, der sich ja gerade dadurch auszeichnet, dass kein Wärmeumsatz stattfindet.
\begin{align}
{ W_V \over Q } = { {\kappa-1} \over {n-\kappa} } \overset{n\rightarrow\kappa}= \infty
~~~\Rightarrow~~~Q= {W_V\over \infty} = 0
\nonumber \\[5px]
\end{align}
Isochorer Prozess
Umgekehrt nähert sich für einen Prozess mit einem Isentropenexponenten n→∞ der Nenner in der Gleichung (\ref{3285}) mehr und mehr dem Wert Unendlich. Bezogen auf den Wärmeumsatz wird dann offensichtlich immer weniger Arbeit verrichtet. Schließlich erhält man für den Sonderfall n=∞ keinen Arbeitsumsatz mehr. Dies entspricht dem isochoren Prozess, der sich genau dadurch auszeichnet, dass keine Arbeit verrichtet wird.
\begin{align}
{ W_V \over Q } = { {\kappa-1} \over {n-\kappa} } \overset{n\rightarrow\infty}= 0
~~~\Rightarrow~~~W_V= {Q \cdot 0} = 0
\nonumber \\[5px]
\end{align}
Isothermer Prozess
Noch ein weiterer Sonderfall zeigt sich anhand der Gleichung (\ref{3285}) für n=1. In diesem Fall ist nämlich der Arbeitsumsatz genauso groß wie der Wärmeumsatz (mit umgekehrten Vorzeichen). Die Energie, die in Form von Wärme am Gas umgesetzt wird, wird also vollständig in Arbeit umgewandelt und umgekehrt. Somit wird die innere Energie des Gases weder verringert noch vergrößert, d.h. sie bleibt konstant. Dies bedeutet in letzter Konsequenz auch eine konstante Temperatur. Der Spezialfall n=1 entspricht also dem isothermen Prozess, der genau dieses charakteristische Merkmal der konstanten Temperatur aufweist.
\begin{align}
{ W_V \over Q } = { {\kappa-1} \over {n-\kappa} } \overset{n\rightarrow 1}= -1
~~~\Rightarrow~~~W_V= -Q
\nonumber \\[5px]
\end{align}
Wichtiger Anwendungsbereich des polytropen Prozesses
Wie bereits ausführlich erläutert können die Polytropengleichungen (\ref{2716}) bis (\ref{7991}) je nach Polytropenexponent n alle bisher betrachteten Spezialfälle wie der isobare (n=0), isotherme (n=1), isentrope (n=κ) und isochore Prozess (n=∞) beschreiben. Auch sind eine Vielzahl anderer thermodynamische Prozesse je nach gewähltem Polytropenexponent beschreibbar. Dennoch gehorchen allerdings nicht alle Zustandsänderungen diesen Polytropengleichungen (z.B. der hier beschriebene Expansionsvorgang, bei dem über eine Zahnstange und ein Zahnrad ein Gewicht mit Hilfe eines Hebels angehoben wird).
Dennoch besitzen polytrope Prozesse vor allem im Exponentenbereich zwischen n=1 (isothermer Prozess) und n=κ (isentroper Prozess) große technische Bedeutung. Denn sehr viele thermodynamische Vorgänge laufen zwischen diesen Grenzfällen ab. Dies wird deutlich, wenn man sich den Ablauf dieser thermodynamischen Prozesse genauer anschaut.
Als Beispiel wird die Kompression einer Luftpumpe bei geschlossen gehaltenem Auslassventil betrachtet. Wird die Kompression (unendlich) langsam durchgeführt, so wird eine Temperaturerhöhung sofort wieder durch Wärmeabgabe an die Umgebung kompensiert. Die Temperatur des Gases wird sich bei diesem Vorgang nicht erhöhen. Die (unendlich) langsame Zustandsänderung stellt folglich ein isothermer Prozess dar – zumindest der beschrieben Prozess zum Komprimieren von Luft mit Hilfe einer Luftpumpe.

Wird die Kompression der Luft hingegen (unendlich) schnell vollzogen, so kann die Temperaturerhöhung nicht kompensiert werden, da dem System keine Zeit bleibt Wärme an die Umgebung abzuführen. Es findet während dieses Vorgangs also keine Wärmeabfuhr statt. Demzufolge handelt es sich bei der (unendlich) schnellen Zustandsänderung um einen isentropen Prozess.
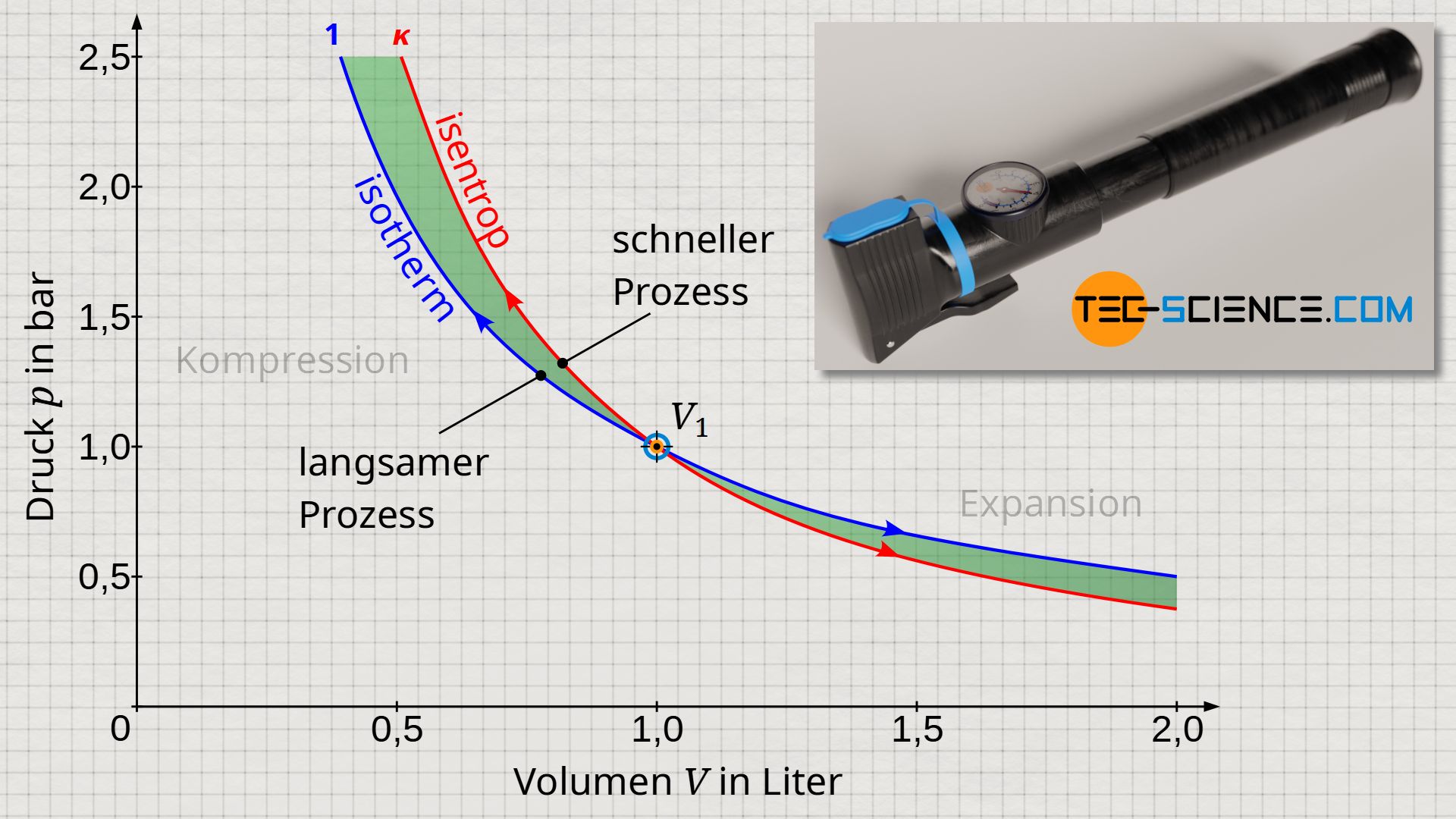
In der Realität kann ein thermodynamischer Prozess jedoch weder unendlich langsam noch unendlich schnell erfolgen, sodass der tatsächliche Prozess zwischen diesen beiden Grenzfällen verlaufen wird. Der Polytropenexponent wird folglich einen Wert zwischen 1 (isothermer Prozess) und κ (isentroper Prozess) aufweisen. Häufig beschränkt sich die Bezeichnung polytroper Prozess auf genau solche Prozesse, deren Polytropenexponenten im Bereich zwischen n=1 und n=κ liegen. Vor allem bei reibungsbehafteten Vorgängen wird die Zustandsänderung häufig mit einer Polytropen angenähert. Mehr Informationen hierzu finden sich auch im Artikel Dissipative thermodynamische Prozesse in adiabaten Systemen.