Isobarer Prozess in einem geschlossenen System

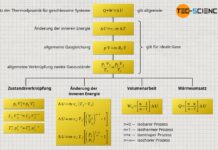
Erfahre in diesem Artikel mehr über die Berechnung von Volumen, Temperatur, Arbeit und Wärme bei einem isobaren Prozess in einem geschlossenen System.

Eine Zustandsänderung bei der sich der Druck nicht ändert, wird auch isobarer Prozess genannt. Somit gilt für alle durchlaufenen Gaszustände derselbe Druck.

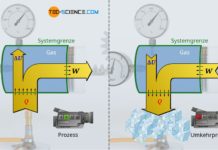
Realisierung eines isobaren Prozesses

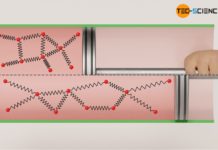
Eine isobare Zustandsänderung in einem geschlossenen System kann zum Beispiel wie folgt realisiert werden. Ein stehender Zylinder ist mit einem Gas gefüllt, der durch einen beweglichen Kolben verschlossen ist. Der Kolben kann zur Steigerung des Druck eventuell noch von oben durch ein konstantes Gewicht belastet werden. Wird das Gas nun erwärmt, so dehnt sich das Gas aus und bewegt den Kolben nach oben. Dabei wird der im Inneren des Zylinders herrschende Druck dem Gas von außen aufgezwungen. Schließlich steht beim Anhebevorgang die Kraft des Gases mit jenen Kräften im Gleichgewicht, die von der anderen Seite auf die Kolbenfläche wirken – zumindest wenn dieses mit konstanter Geschwindigkeit angehoben wird (Kräftegleichgewicht), wovon an dieser Stelle ausgegangen werden soll.

Anhand der „äußeren“ Kräfte kann demzufolge die „innere“ Kraft des Gases ermittelt werden und über die Kolbenfläche A dann schließlich der Gasdruck p. Im vorliegenden Fall wirkt als „äußere“ Kraft zum einen die Gewichtskraft F_G des Kolbens (inklusive evtl. auferlegter Gewichte). Zum anderen wirkt ebenfalls von außen die Kraft F_u auf den Kolben, die aufgrund des Umgebungsdrucks zustande kommt! Diese kann anhand des Umgebungsdruckes p_u und der Kolbenfläche A berechnet werden (F_u=p_u⋅A). Somit gilt für die auszuübende Kraft F_gas des Gases:

\begin{equation}
F_\text{gas} \overset{!}{=} F_\text{G} + F_\text{u} ~~~~~\text{Kräftegleichgewicht} \\[5px]
F_\text{gas} = F_\text{G} + p_\text{u} \cdot A \\[5px]
\end{equation}

Das Gas wirkt mit dieser Kraft F_gas auf die Kolbenfläche A, was entsprechend zu folgendem Gasdruck p führt:

\begin{equation}
\label{de}
\underline{p} = {F_\text{gas} \over A} = {{F_\text{G} + p_\text{u} \cdot A} \over A} = \underline{ {F_\text{G} \over A} + p_\text{u}}
\end{equation}

Gleichung (\ref{de}) macht nun deutlich, dass der Gasdruck offensichtlich nur von Größen abhängt, die sich während des Prozesses nicht ändern. Der Gasdruck bleibt somit für die gesamte Zustandsänderung stets konstant. Beim Heben des Kolbens handelt es sich folglich um einen isobaren Prozess.

Darstellung im Volumen-Druck-Diagramm

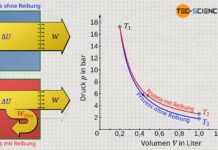
Wird der Kolben schließlich unter Wärmezufuhr nach oben bewegt, so erwärmt sich das Gas ausgehend der Anfangstemperatur T₁ auf einen Endwert T₂. Dabei vergrößert sich das Gasvolumen bei konstantem Druck p vom Ausgangsvolumen V₁ auf ein Endvolumen V₂. Wird dieser Prozess im p(V)-Diagramm abgebildet, so ergibt sich bei konstantem Druck p eine horizontale Linie vom Anfangsvolumen V₁ zum Endvolumen V₂.

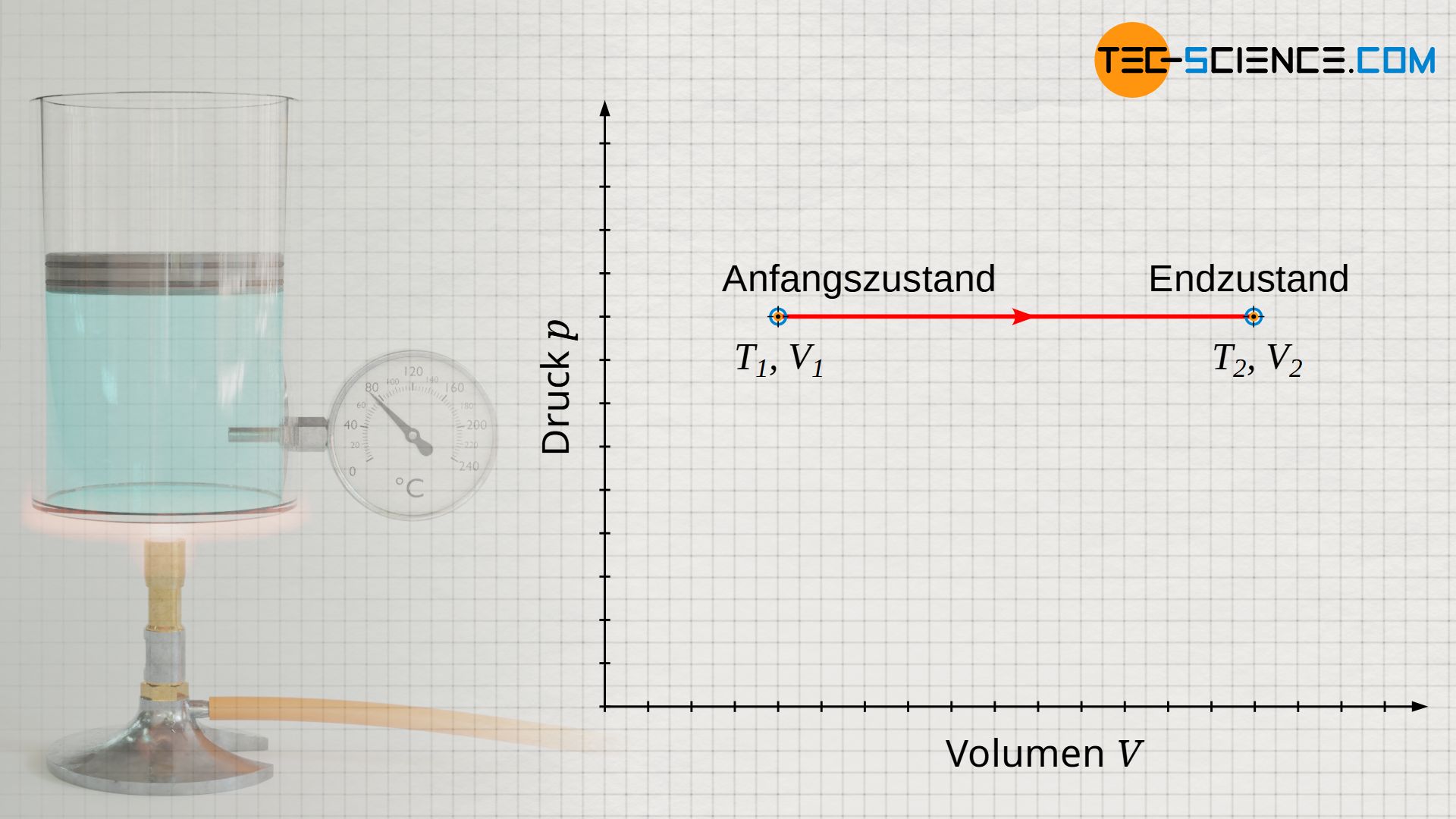
Zusammenhang zwischen Volumen und Temperatur (Gesetz von Gay-Lussac)

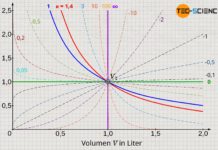
Bei einem isobaren Prozess steigt das Volumen proportional mit der Temperatur an. Diese Aussage gilt allerdings nur, wenn die Temperatur in der Einheit Kelvin angegeben wird. Eine Verdopplung der Temperatur bei einer isobaren Erwärmung bedeutet somit auch eine Verdopplung des Gasvolumens. Diese Proportionalität ist gleichbedeutend mit der Aussage, dass Volumen und Temperatur bei einem isobaren Prozess stets in einem konstanten Verhältnis zueinander stehen. Diese Gesetzmäßigkeit bezeichnet man auch als Gesetz von Gay-Lussac:

\begin{align}
&V \sim T ~\Rightarrow~ {V \over T} = \text{konstant}
\end{align}

Zwei beliebige Zustände innerhalb eines isobaren Prozesses sind folglich durch den konstanten Quotienten von Volumen und Temperatur miteinander verknüpft:

\begin{equation}
\label{p} 
\boxed{ {V_1 \over T_1} = {V_2 \over T_2} } ~ \text{Gesetz von Gay-Lussac}
\end{equation}

Berechnung der Änderung der inneren Energie

Für ideale Gase ergibt sich die Änderung der inneren Energie ΔU unabhängig des thermodynamischen Prozesses lediglich anhand der Temperaturänderung ΔT=T₂-T₁:

\begin{equation}
\label{du} 
\boxed{ \Delta U = c_\text{v} ~ m ~ \left(T_2-T_1 \right)} = c_\text{v} ~ m ~ T_1 ~ \left({T_2 \over T_1}-1 \right) = c_\text{v} ~ m ~ T_1 ~ \left({V_2 \over V_1}-1 \right)
\end{equation}

Darin bezeichnet m die Gasmasse und c_v die spezifische Wärmekapazität des Gases. Wird Gleichung (\ref{du}) nach Ausklammerung der Temperatur T₁ mit Gleichung (\ref{p}) verknüpft, so kann die Änderung der inneren Energie auch anhand des Volumenverhältnisses V₂/V₁ (=T₂/T₁) ausgedrückt werden.

Berechnung der Volumenänderungsarbeit

Die am Gas bzw. vom Gas verrichtete Volumenänderungsarbeit ergibt sich für den isobaren Fall relativ einfach als Rechteckfläche unter der Kurve im p(V)-Diagramm (Beachte, dass die Fläche unter der Prozesskurve ganz allgemein die umgesetzte Volumenänderungsarbeit darstellt). Die Rechteckfläche bestimmt sich dabei über die „Höhe“ p und die „Breite“ ΔV=V₂-V₁. Unter Berücksichtigung der Vorzeichenkonvention gilt für die umgesetzte Volumenänderungsarbeit W_V des isobaren Prozesses somit die nachfolgende Gleichung:

\begin{equation}
\label{w}
\boxed{ W_\text{V} = – p \cdot \Delta V = – p \cdot \left(V_2 – V_1 \right) }
\end{equation}

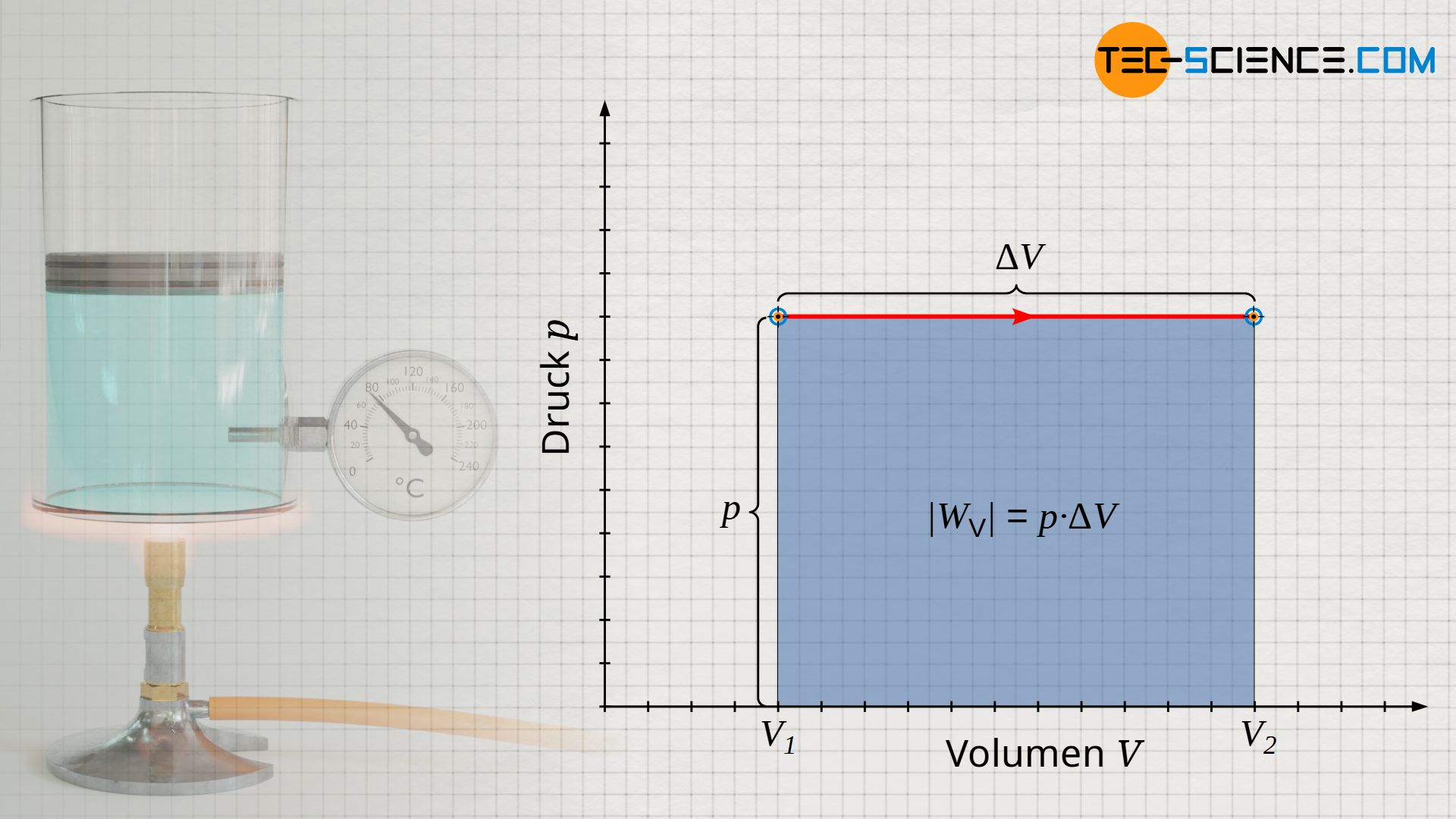
Anmerkung: Das Minuszeichen ist der Vorzeichenkonvention geschuldet, da bei Volumenvergrößerung (Expansion: ΔV>0) das Gas offensichtlich Arbeit verrichtet und dieser Arbeitsumsatz negativ zu werten ist (W_V<0). Umgekehrt drückt sich eine Volumenverkleinerung (Kompression: ΔV<0) vorzeichenrichtig in einem positiven Arbeitsumsatz aus (W_V>0), da dabei Arbeit dem Gas zugeführt wird.

Die Volumenänderungsarbeit kann nicht nur über die Differenz der Volumina, sondern auch über die Differenz der Temperaturen ermittelt werden. Hierzu sind einige Umformungen nötigt. Zunächst wird der Druck p in Gleichung (\ref{w}) in den Klammerterm hinein multipliziert. Anschließend wird ausgenutzt, dass gemäß der thermischen Zustandsgleichung für das Produkt aus Druck und Volumen gilt:

\begin{align}
\label{z}
\boxed{p \cdot V= R_\text{s} \cdot m \cdot T} ~~~\text{ideales Gasgesetz}
\end{align}

Darin bezeichnet R_s die spezifische Gaskonstante des eingeschlossenen Gases. Anschließend kann der Term R_S⋅m wieder vor die Klammer gezogen werden:

\begin{align}
\label{www}
W_\text{V} &=- p \cdot \left(V_2 – V_1 \right) \\[5px]
&=- \left( p ~ V_2 – p ~ V_1 \right) ~\text{ mit }~ \underbrace{p~V=R_\text{s}~m~T}_{\text{ideales Gasgesetz}} ~\text{ folgt:}~ \\[5px]
&= – \left( R_\text{s} ~ m ~ T_2 – R_\text{s} ~ m ~ T_1 \right) \\[5px]
&= -R_\text{s} ~ m ~ \left(T_2 – T_1 \right)
\end{align}

Die Volumenänderungsarbeit W_V lässt sich also auch über die Differenz zwischen End- und der Anfangstemperatur des isobaren Prozesses ermitteln:

\begin{equation}
\label{wvv}
\boxed{W_\text{V} = – R_\text{s} ~ m ~ \left(T_2 – T_1 \right)}
\end{equation}

Berechnung der Wärmeenergie

Mit Hilfe des ersten Hauptsatzes der Thermodynamik lässt sich schließlich auch die zu- oder abgeführte Wärmeenergie Q während einer isobaren Zustandsänderung berechnen. Sie ermittelt sich aus der Differenz der Änderung der inneren Energie ΔU und der Volumenänderungsarbeit W_V. Für die Volumenänderungsarbeit soll an dieser Stelle ausdrücklich Gleichung (\ref{wvv}) zur Anwendung kommen, da sich dabei tiefergehende Vereinfachungen ergeben:

\begin{align}
&\boxed{W_V + Q = \Delta U} ~~~ \text{Erster Hauptsatz}  \\[5px]
\end{align}

\begin{align}
Q &= \Delta U – W_V \\[5px]
&= c_\text{v} ~ m ~ \left(T_2-T_1 \right) + R_\text{s} ~ m ~ \left(T_2 – T_1 \right) \\[5px]
&= \underbrace{[c_\text{v}+R_\text{s}]}_{=c_\text{p}} ~ m ~ (T_2-T_1)
\label{eq:9885}
\end{align}

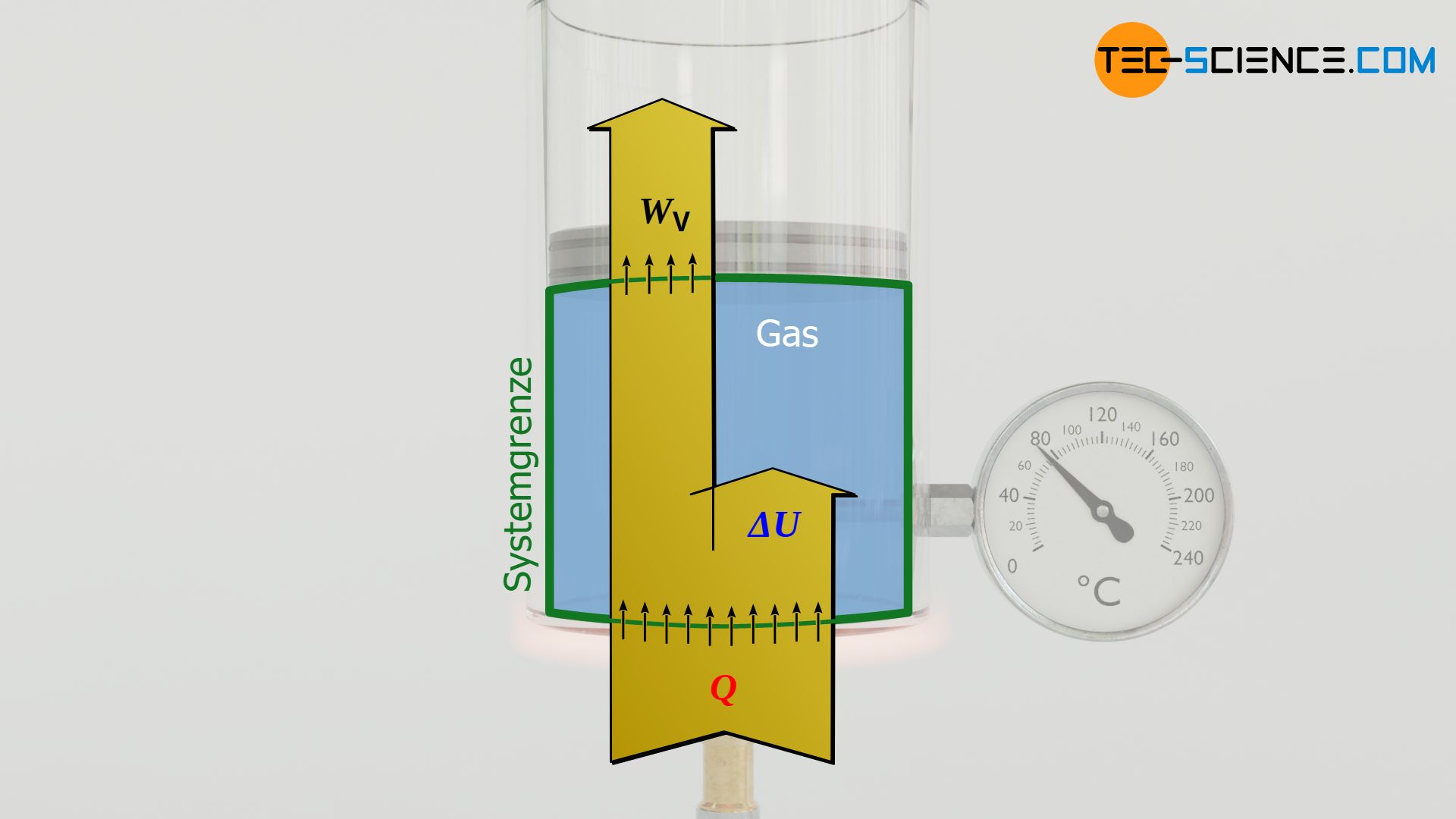
Während der Umformung werden die Stoffkonstanten c_v und R_s zu einer neuen Konstante c_p zusammengefasst, sodass sich letztlich folgender Zusammenhang zwischen dem Wärmeumsatz Q und der Temperaturänderung ergibt:

\begin{equation}
\label{q} 
\boxed{ Q = c_\text{p} ~ m ~ (T_2-T_1)} ~\text{mit}~ \boxed{c_\text{p}=c_\text{v}+R_\text{s}}
\end{equation}

Der Grund weshalb diese Konstanten so zusammengefasst werden, zeigt sich wenn man die obere Formel mit der Formel für die übertragene Wärme des isochoren Prozesses vergleicht:

\begin{align}
\label{eq:6667}
Q_\text{v} &= c_\text{v} ~ m ~ (T_2-T_1) ~~ \text{isochorer Prozess} \\[5px]
Q_\text{p} &= c_\text{p} ~ m ~ (T_2-T_1) ~~ \text{isobarer Prozess}\\[5px]
\end{align}

Es lässt sich darin die Konstante c_v als die spezifische Wärmekapazität des isochoren Prozesses und c_p als die spezifische Wärmekapazität des isobaren Prozesses interpretieren. Auf diese Weise ergeben sich nun sowohl beim isobaren als auch beim isochoren Prozess die analogen Beziehungen zwischen der übertragenen Wärme und der Temperaturänderung

Der Wärmeumsatz gemäß Gleichung (\ref{q}) kann bei gegebener Anfangstemperatur T₁ auch durch das Verhältnis von End- und Anfangsvolumen ausgedrückt werden:

\begin{equation}
Q= c_\text{p} ~ m ~ \left(T_2-T_1 \right) = c_\text{p} ~ m ~ T_1 ~ \left({T_2 \over T_1}-1 \right) = c_\text{p} ~ m ~ T_1 ~ \left({V_2 \over V_1}-1 \right)
\label{eq:7052}
\end{equation}

Anmerkung zu den spezifischen Wärmekapazitäten

Beachte, dass aus Gleichung (\ref{q}) hervorgeht, dass die spezifische Wärmekapazität des isobaren Prozesses c_p stets um den Wert der spezifischen Gaskonstante R_s größer ist als die spezifische Wärmekapazität des isochoren Prozesses. Dies bedeutet, dass bei einem isobaren Prozess offensichtlich mehr Wärme zuzuführen ist als bei einem isochoren Vorgang, wenn dabei dieselbe Temperaturänderung erzielt werden soll.

Der anschauliche Grund hierfür ist, dass bei einem isobaren Prozess die zugeführte Wärmeenergie Q nicht vollständig der Änderung der inneren Energie ΔU und somit der Temperaturerhöhung zugutekommt. Ein Teil der zugeführten Wärme wird nämlich in Volumenänderungsarbeit W_V gesteckt. Aus diesem Grund muss mehr Wärmeenergie zugeführt werden, damit abzüglich dieser Volumenänderungsarbeit noch genügend Energie für die Änderung der inneren Energie und somit für die Temperaturerhöhung zur Verfügung steht.

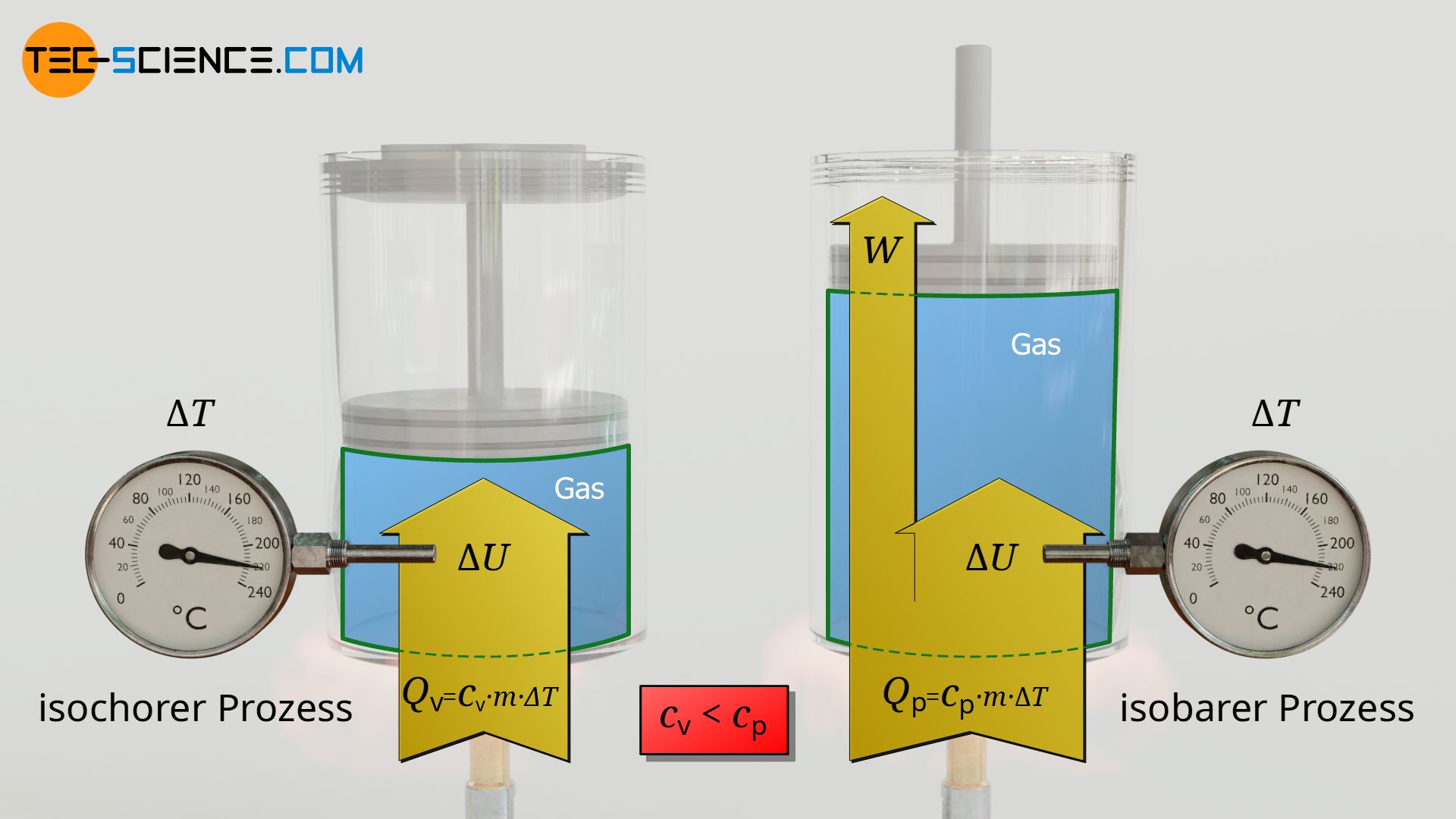
Die Herleitung nach Gleichung (\ref{www}) macht deutlich, dass die spezifische Gaskonstante R_s überhaupt erst durch den Term der Volumenänderungsarbeit zustande kommt. Für weitere Informationen, siehe auch den Artikel Spezifische Wärmekapazität von Gasen.