Erfahre in diesem Artikel, wie sich mit Hilfe der Van-der-Waals-Gleichung die Verflüssigung von Gasen bei hohen Drücken erklären lässt.
Van-der-Waals-Gleichung
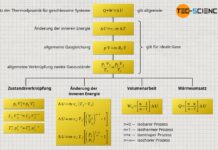
Die ideale Gasgleichung beschreibt unter vereinfachten Bedingungen das Verhalten von idealen Gasen. Bei ausreichend hohen Temperauren und nicht allzu großen Drücken, liefert diese Gleichung auch für reale Gase brauchbare Vorhersagen. In allen anderen Fällen, muss die ideale Gasgleichung zur sogenannten Van-der-Waals-Gleichung erweitert werden. Diese berücksichtigt für reale Gase sowohl das Eigenvolumen der Teilchen als auch die zwischenmolekularen Anziehungskräfte:
\begin{align}
&\boxed{\left(p+\frac{a}{V_\text{m}^2}\right) \cdot \left(V_\text{m} – b\right) = R_\text{m} \cdot T} ~~~\text{mit}~~~\boxed{V_\text{m}=\frac{V}{n}}~~\text{molares Volumen} \\[5px]
\end{align}
Darin bezeichnet a den sogenannten Binnendruck aufgrund der gegenseitigen Wechselwirkung der Moleküle, während das Kovolumen b das Eigenvolumen der Gasmoleküle berücksichtigt. Beide Größen sind von der Art des Gases abhängig (siehe Tabelle unten). Ferner beschreibt das molare Volumen Vm das vom Gas eingenommene Volumen pro Mol an Teilchen (Quotient aus geometrischem Volumen V und Stoffmenge n). Rm bezeichnet die universelle Gaskonstante und T die Temperatur in der Einheit Kelvin. Mehr Informationen zur Van-der-Waals-Gleichung und deren Herleitung finden Sie im Artikel Van-der-Waals-Gleichung (Gasgesetz für reale Gase).
| Gasart | Binnendruck a in 10-3 J⋅m³/mol² | Kovolumen b in 10-6 m³/mol |
|---|---|---|
| Ammoniak (NH3) | 424 | 37 |
| Argon (Ar) | 136 | 32 |
| Chlor (Cl2) | 655 | 56 |
| Helium (He) | 3,45 | 24 |
| Kohlendioxid (CO2) | 365 | 43 |
| Luft | 136 | 37 |
| Methan (CH4) | 230 | 43 |
| Neon (Ne) | 21 | 17 |
| Propan (C3H8) | 93 | 90 |
| Sauerstoff (O2) | 138 | 32 |
| Stickstoff (N2) | 141 | 39 |
| Wasser (H2O) | 553 | 30 |
| Wasserstoff (H2) | 25 | 27 |
Erklärung der Verflüssigung von Gasen bei hohen Drücken
Mit Hilfe der Van-der-Waals-Gleichungen lässt sich nicht nur das Verhalten von realen Stoffen in der Gasphase beschreiben, sondern es kann damit auch der Phasenübergang vom gasförmigen Zustand in den flüssigen Zustand bei hohen Drücken erklärt werden. Um dies zu zeigen, wird die Van-der-Waals-Gleichung zunächst so umgestellt, dass sich der Druck p in Abhängigkeit des Volumens Vm darstellen lässt:
\begin{align}
&\boxed{p(V_\text{m}) = \frac{R_\text{m} \cdot T}{V_\text{m} – b} – \frac{a}{V_\text{m}^2} } \\[5px]
\end{align}
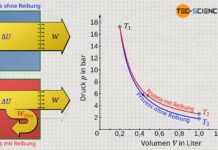
Am Beispiel von Kohlendioxid zeigt das abgebildete Volumen-Druck-Diagramm den Druckverlauf in Abhängigkeit des Volumens bei einer Temperatur von 283 K. Dieses Diagramm zeigt im Prinzip die isotherme Kompression von zunächst gasförmigem Kohlenstoffdioxid. Man kann sich hierzu ein Mol an Kohlenstoffmoleküle vorstellen, die zunächst ein Volumen von 800 cm³ einnehmen (Zustand 1). In diesem Zustand beträgt der Druck rund 25 bar. Wird das Volumen nun isotherm verkleinert, so steigt der Druck erwartungsgemäß an. Bei einem Volumen von 175 cm² hat sich der Druck auf fast 60 bar erhöht (Zustand 2).
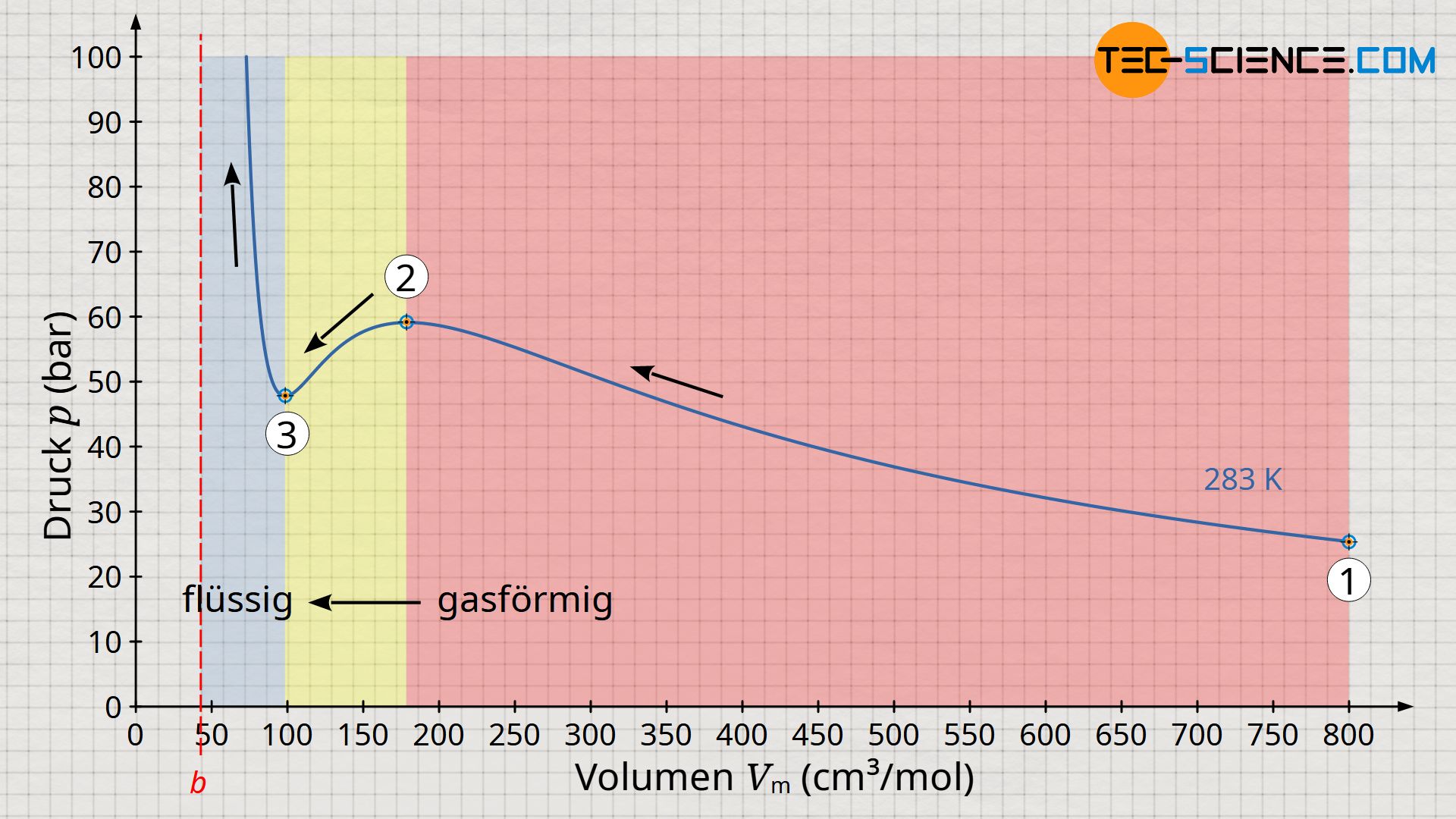
Bei weiterer Volumenverkleinerung passiert nun allerdings etwas paradoxes (Zustandsänderung von 2 nach 3). Gemäß der abgebildeten Funktion verringert sich der Druck bei weiterer Kompression. Die Erfahrung zeigt jedoch, dass eine Kompression nicht plötzlich eine Verringerung des Drucks zu Folge haben kann. Tatsächlich spiegelt die Van-der-Waals-Gleichung in diesem Bereich nicht mehr das korrekte Verhalten wieder! Erst unterhalb eines Volumens von etwa 100 cm³ geht eine weiter Kompression wieder wie gewohnt mit einer Druckerhöhung einher. Dabei steigt der Druck allerdings extrem stark an, wie man es eigentlich nur von Flüssigkeiten her kennt. Und tatsächlich handelt es sich dabei um die flüssige Phase des Kohlendioxids, welches sich aufgrund des hohen Druck verflüssigt hat.
Eine solche Verflüssigung bei hohen Drücken findet häufig Anwendung beim Abfüllen von Gasen in Gasflaschen, deren Inhalt aufgrund des hohen Drucks verflüssigt wird. Begrenzt wird das minimale Volumen des verflüssigten Gases durch das Eigenvolumen der Moleküle, welches gemäß der Van-der-Waals-Gleichung durch das Kovolumen b bestimmt ist. Bei Annäherung des Volumens an das Kovolumen b steigt der Druck somit ins Unendliche.
Bei Betrachtung des Volumen-Druck-Diagramms könnte man vorschnell meinen, dass sich die Verflüssigung zwischen dem Hochpunkt (2) und Tiefpunkt (3) vollzieht. Die Realität zeigt allerdings, dass eine isotherme Verflüssigung bei konstantem Druck stattfindet, dem sogenannten Sättigungsdampfdruck. Wie muss also diese horizontale Linie der Verflüssigung im Diagramm verlaufen? An dieser Stelle sei auf den Artikel Volumenänderungsarbeit verwiesen, in dem ausführlich erläutert wurde, dass die Fläche im Volumen-Druck-Diagramm die Dimension einer Energie hat.
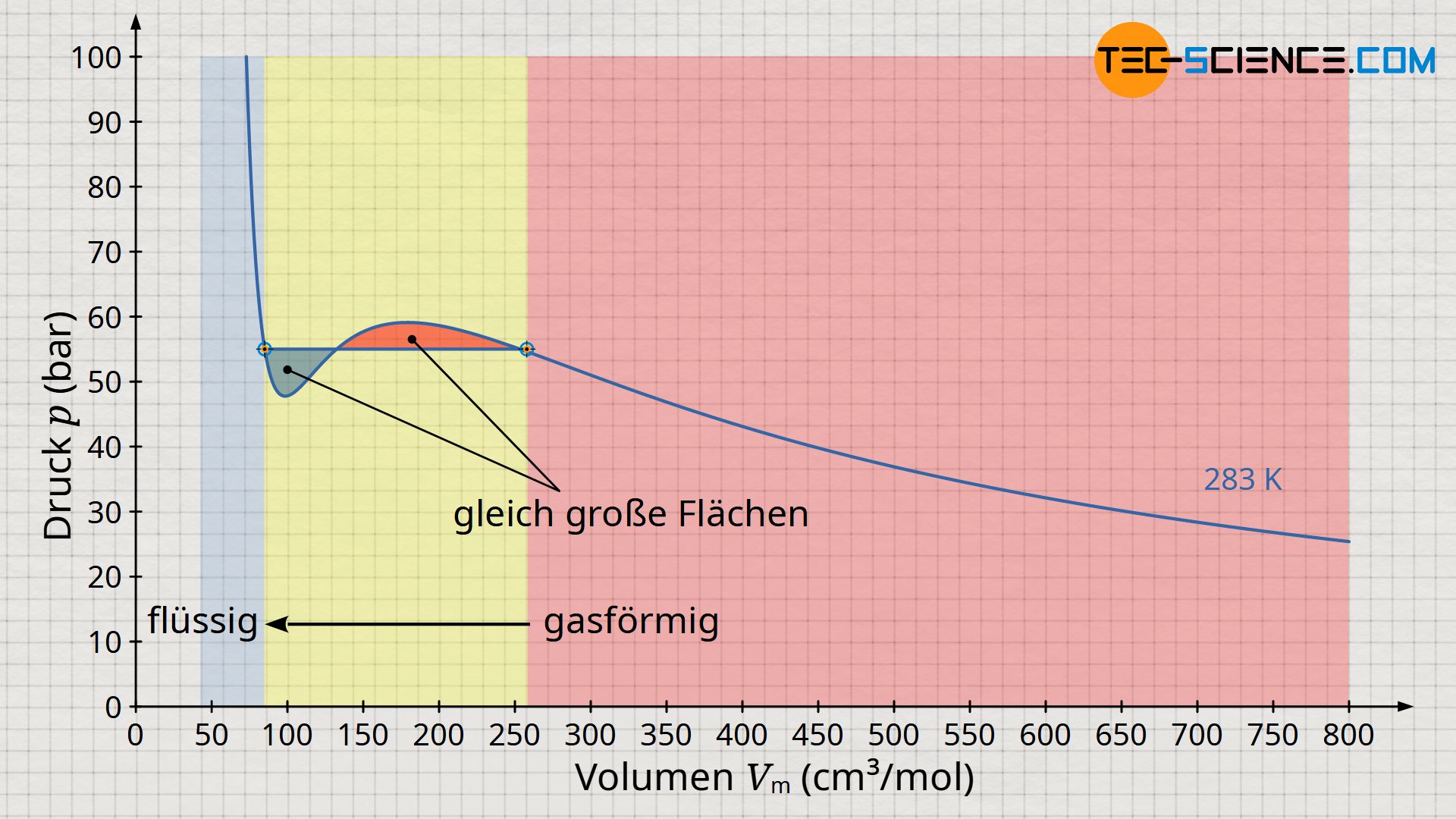
Um den Energieerhaltungssatz für einen reversiblen Vergleichsprozess also nicht zu verletzen, muss die horizontale Linie zur Beschreibung der Verflüssigung folglich so verlaufen, dass die sich im Diagramm bildenden Flächen unterhalb und oberhalb der Horizontalen gleich groß sind (sogenannte Maxwell-Konstruktion). Die Kurve, die sich rein mathematisch aus der Van-der-Waals-Gleichung ergibt und die sich um die horizontale Linie „schlängelt“ wird auch als Van-der-Waals-Schleife bezeichnet. Die horizontale Linie selbst wird auch Maxwell-Gerade genannt und entspricht dem Sättigungsdampfdruck.
Die im Bereich der Verflüssigung eingeschlossenen Flächen zwischen Maxwell-Gerade (Sättigungsdampfdruck) und Van-der-Waals-Schleife müssen aus energetischen Gründen gleich groß sein!
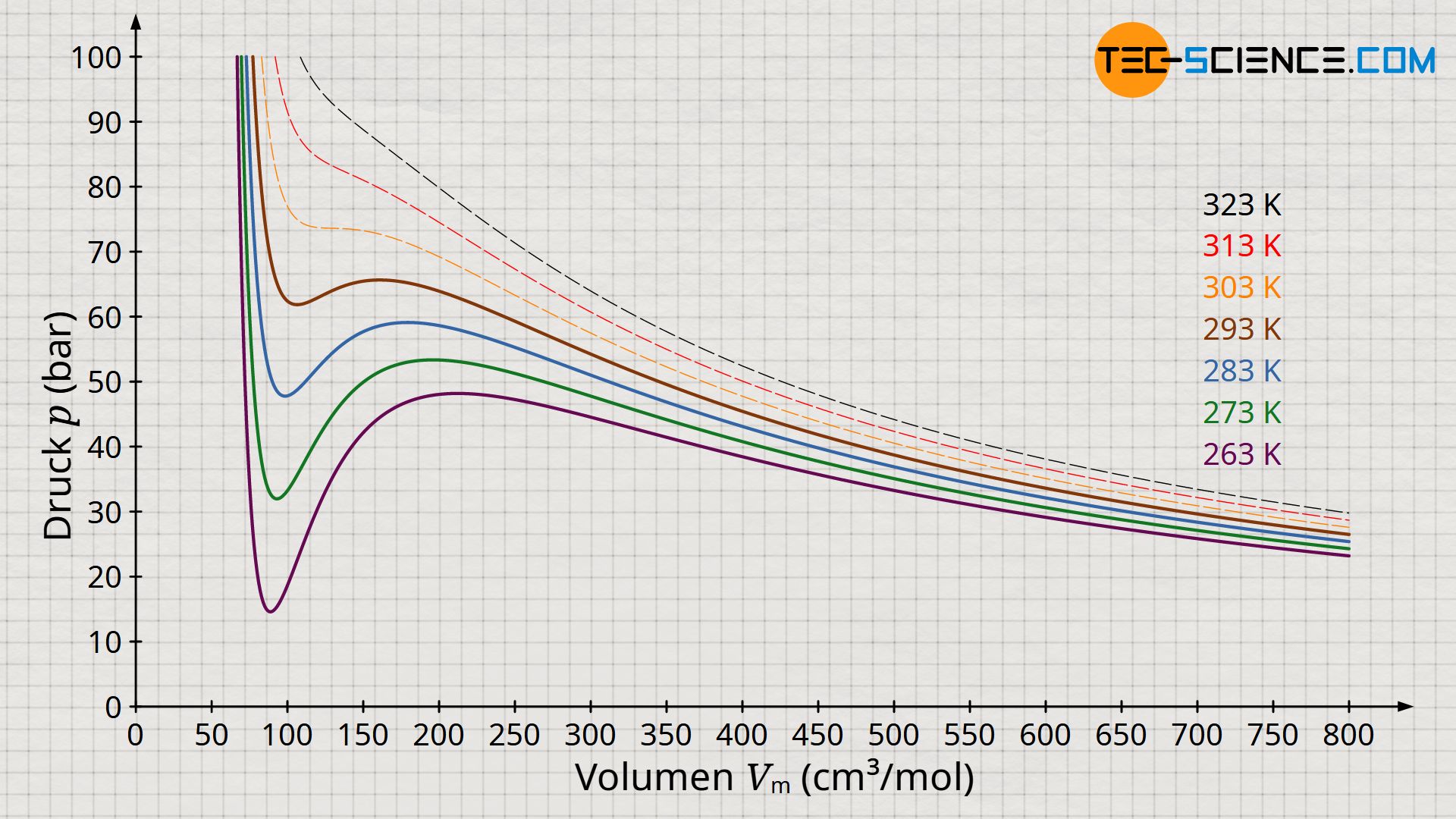
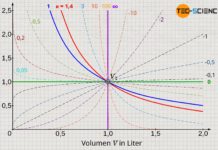
Die obere Abbildung zeigt den Druckverlauf gemäß der Van-der-Waals-Gleichung für weitere Isothermen. Gemäß der Maxwell-Konstruktion ergibt sich somit ein charakteristisches Phasendiagramm, welches den Übergang vom gasförmigen in den flüssigen Zustand für ausgewählte Temperaturen anschaulich beschreibt (Diagramm unten). Dabei zeigt sich, dass ab einer bestimmten Temperatur die Van-der-Waals-Gleichung keine Schleife mit Hoch- und Tiefpunkten mehr zeigt, sondern in diesem Grenzfall nur noch einen horizontalen Wendepunkt. Man bezeichnet diesen Punkt auch als kritischen Punkt. Zustandsänderungen oberhalb dieses kritischen Punktes vollziehen sich ohne klassischen Phasenübergang!
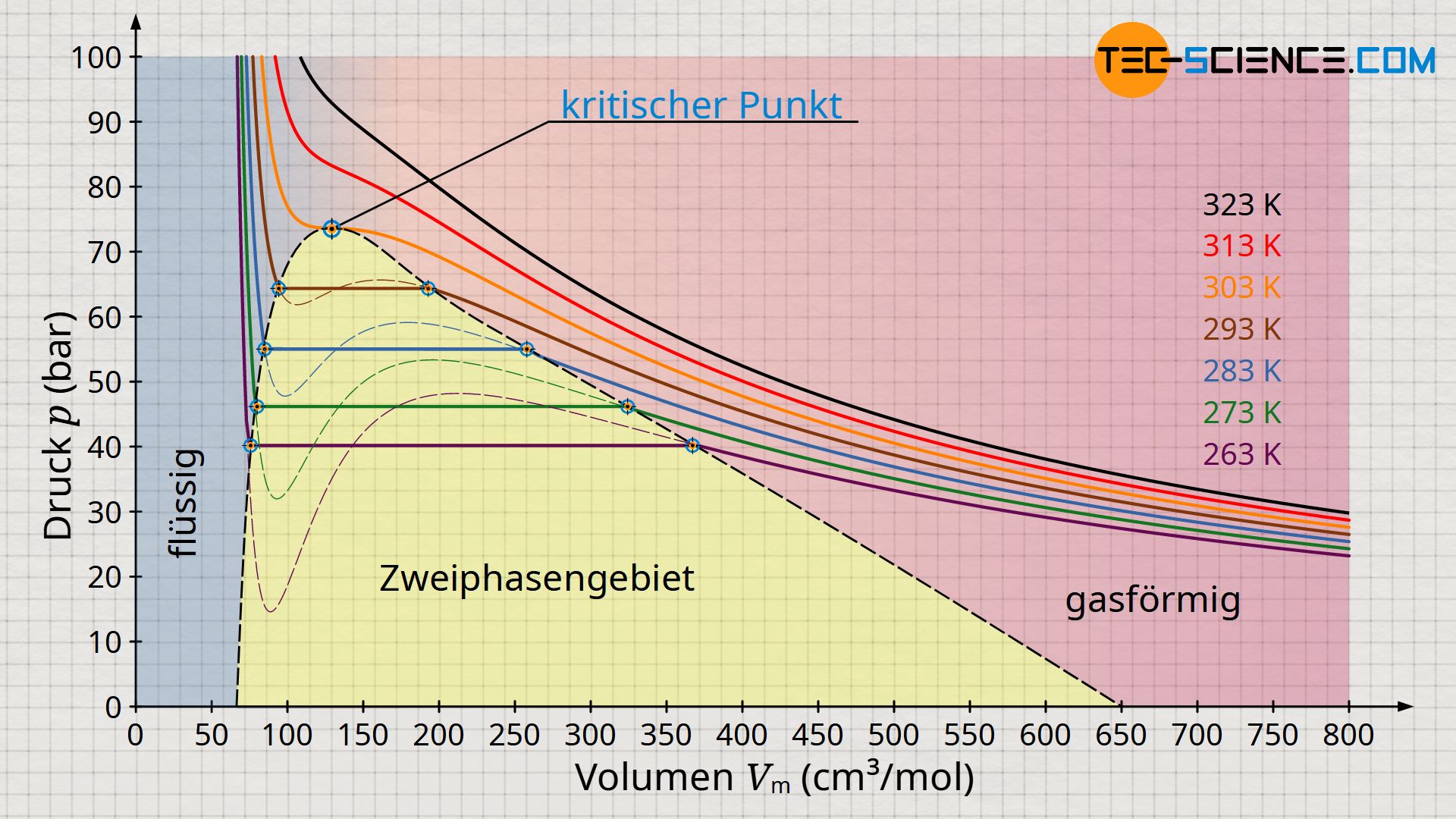
Bei solchen überkritischen Zustandsänderungen gibt es also keinen sichtbaren Phasenübergang mehr. Während sich die klassischen Phasenübergänge durch sprunghafte Änderungen in den physikalischen Eigenschaften wie bspw. Volumen, Dichte, Wärmekapazität, Wärmleitfähigkeit, etc. bemerkbar machen, fehlen bei überkritischen Zuständen solche Merkmale. Man kann folglich nicht mehr zwischen flüssigen oder gasförmigen Zuständen unterscheiden. Es handelt sich also um einen kontinuierlichen Übergang der Eigenschaften ohne dem Stoff dabei einen typischen Aggregatzustand zuschreiben zu können.
Überkritische Zustandsänderungen werden technisch zum Beispiel bei modernen Dampfkraft-Kraftwerksprozessen angewendet, mit denen sich thermische Wirkungsgrade von über 50 % realisieren lassen.