Erfahre in diesem Artikel mehr über die Entstehung der Celsius-, der Fahrenheit- und der Kelvin-Temperaturskala.
Einleitung
Im Alltag versteht man unter der Temperatur eines Stoffes häufig die Eigenschaft „warm“ bzw. „kalt“ zu sein. Tatsächlich hängt ein solches Wärmeempfinden jedoch von verschiedenen Faktoren ab. Unter anderem von der thermischen Leitfähigkeit des Stoffes. So fühlt sich zum Beispiel Metall aufgrund der höheren thermischen Leitfähigkeit bei Kälte deutlich kühler an als Holz, obwohl beide dieselbe Temperatur besitzen.

Zum anderen hängt das menschliche Temperaturempfinden von der „Vorgeschichte“ unserer Haut ab, mit der wir Gegenstände berühren. Halten wir zum Beispiel eine Hand in Eiswasser und stecken diese anschließend in ein Topf mit warmem Wasser, dann fühlt sich dies deutlich heißer an im Vergleich zum Temperaturempfinden mit der ungekühlten Hand.

Die Temperatur eines Stoffes über das menschliche Empfinden „warm“ oder „kalt“ zu sein zu definieren, scheitert also. Für die Festlegung der Temperatur bedient man sich deshalb eines weiteren Zusammenhangs der direkt mit der Temperatur verknüpft ist: Nämlich die Bewegung der Teilchen in einem Stoff. Wie bereits im Artikel „Temperatur und Teilchenbewegung“ ausführlich erläutert, ist die Temperatur eines Stoffes nämlich ein Maß für die Bewegungsenergie der darin enthaltenen Teilchen (genauer gesagt: ein Maß für die mittlere kinetische Energie eines Teilchens).
Die Temperatur ist ein Maß für die Bewegungsenergie eines Teilchens in einem Stoff!
Diese Bewegungsenergie macht sich unter anderem in der thermischen Ausdehnung von Stoffen bemerkbar. Bei hohen Temperaturen sind die Teilchen nämlich sehr stark in Bewegung und nehmen somit einen größeren Raum ein. In Flüssigkeitsthermometern wird genau dieses Prinzip der Wärmeausdehnung genutzt um die Temperatur zu bestimmen. Dabei dehnt sich eine thermometrische Flüssigkeit* in einem Steigrohr (auch Kapillare genannt) bei Erwärmung aus und zieht sich bei Abkühlung zusammen. An einer geeichten Skala kann man dann die jeweilige Temperatur ablesen, die zur entsprechenden Wärmeausdehnung geführt hat.

Je nachdem welche Fixpunkte für die Festlegung der Skala und damit zur Messung der Temperatur zugrundegelegt werden, unterscheidet man hauptsächlich drei Temperaturskalen:
- Celsius-Skala
- Fahrenheit-Skala
- Kelvin-Skala
Auf die verschiedenen Temperaturskalen wird in den folgenden Abschnitten näher eingegangen.
*) eine Flüssigkeit wird als thermometrisch bezeichnet, wenn sich ihr Volumen gleichmäßig mit der Temperatur ändert und damit zur Verwendung in Flüssigkeitsthermometern geeignet ist. Früher wurde hierfür das hochgiftige Quecksilber verwendet; heutzutage kommt eine eingefärbte Alkoholmischung zum Einsatz (z.B. Ethanol).
Celsius-Skala
Im Alltag ist es üblich die Temperatur von Stoffen mithilfe der sogenannten Celsius-Skala zu messen. Bei der damaligen Festlegung der Celsius-Skala durch den schwedischen Astronom Anders Celsius wurde auf zwei Fixpunkte zurückgegriffen. Zum einen auf den Schmelzpunkt von Wasser und zum anderen auf dessen Siedepunkt (jeweils bei Umgebungsdruck von 1 bar).

Der Schmelzpunkt von Wasser wurde dabei willkürlich als Wert 0 definiert, während der Siedepunkt des Wassers – ebenfalls ohne tieferen physikalischen Grund – den Wert 100 bekam. Alle weiteren Temperaturen können durch inter– bzw. extrapolieren dieser Grundskala erhalten werden. Die Temperaturwerte wie sie auf der Celsiusskala erhalten werden, bekommen die Einheit Grad Celsius (°C). Als Symbol für die Temperatur der Celsiusskala wird häufig das griechische Symbol ϑ verwendet.
Fahrenheit-Skala
Der deutsche Physiker Daniel Fahrenheit wollte für den Alltag negative Temperaturwerte auf seiner Temperaturskala vermeiden. Deshalb machte er sich im 17 Jahrhundert (weit vor Celsius) Gedanken über die tiefst mögliche Temperatur, die er im Labor ohne technische Hilfsmittel herstellen konnte.
Er experimentierte hierzu mit einer Kältemischung aus Wasser, Eis, und Ammoniumchlorid und konnte damit eine minimale Temperatur von -17,8 °C herstellen. Diesen Temperaturpunkt nutzte er für die Festlegung des Nullpunktes seiner Fahrenheitskala (0 °F). Als weiteren Referenzpunkt nutzte Fahrenheit die Körpertemperatur des Menschen und ordnete dieser den Wert 100 °F (37,8 °C) zu. Die Temperaturwerte wie sie auf der Fahrenheitskala erhalten werden, bekommen die Einheit Grad Fahrenheit (°F).

Der entscheidende Nachteil der Fahrenheit-Skala ist, dass vor allem der oberste Fixpunkt der durch die Körpertemperatur definiert ist, nicht exakt reproduzierbar ist. Jeder Mensch hat je nach Tagesform und körperliche Betätigung eine andere Körpertemperatur.
Deshalb nutzt man für die heutige Definition der Fahrenheitskala andere Fixpunkte, nämlich der Gefrierpunkt des Wassers mit 32 °F (0°C) und die Siedetemperatur mit 212 °F (100 °C). Zwischen Gefrier- und Siedepunkt des Wasser liegen folglich 180 Grade und nicht wie bei der Celsiusskala 100 Grade. Ändert sich die Temperatur in der Celsiusskala um 1 Grad, dann ändert sich der Temperaturwert in der Fahrenheitskala folglich um 1,8 Grad. Zudem muss für den Temperaturwert die Verschiebung des Nullpunktes für den Gefrierpunkt von Wasser berücksichtigt werden (32°F). Für die Umrechnung eines Temperaturwertes von der Celsiusskala in die Fahrenheitskala gilt folglich:
\begin{align}
&\boxed{ [°F] = [°C] \cdot 1,8 + 32} \\[5px]
\end{align}
Umgekehrt gilt für die Umrechnung einer gegebenen Temperatur in der Einheit Fahrenheit nach Celsius folgende Formel:
\begin{align}
&\boxed{ [°C] = \frac{[°F] – 32}{1,8} } \\[5px]
\end{align}
Die untere Abbildung zeigt die beiden Temperaturskalen im Vergleich.

Kelvin-Skala
Die Celsius-Skala und auch die Fahrenheit-Skala sind aufgrund der willkürlichen Festlegung der Fixpunkte nicht sehr wissenschaftlich. Vielmehr sollte eine sinnvolle Temperaturskala den Sachverhalt berücksichtigen, dass die Temperatur ein Maß für die Bewegung der Teilchen darstellt. Jener Temperaturpunkt in dem die Teilchen keinerlei Bewegungsenergie mehr besitzen (also völlig in Ruhe sind), sollte deshalb auch als Referenzpunkt einer physikalisch sinnvollen Temperaturskala zugrunde gelegt werden.
Einen solchen „Bewegungsnullpunkt“ nutzt man bei der Festlegung der sogenannten Kelvin-Skala. Dabei wird jener Temperaturpunkt als Wert Null definiert, in dem die Teilchen eines Stoffes keine Geschwindigkeit mehr besitzen. Dieser Temperaturnullpunkt stellt folglich die niedrigst mögliche Temperatur dar und wird deshalb auch als absoluter Nullpunkt bezeichnet.
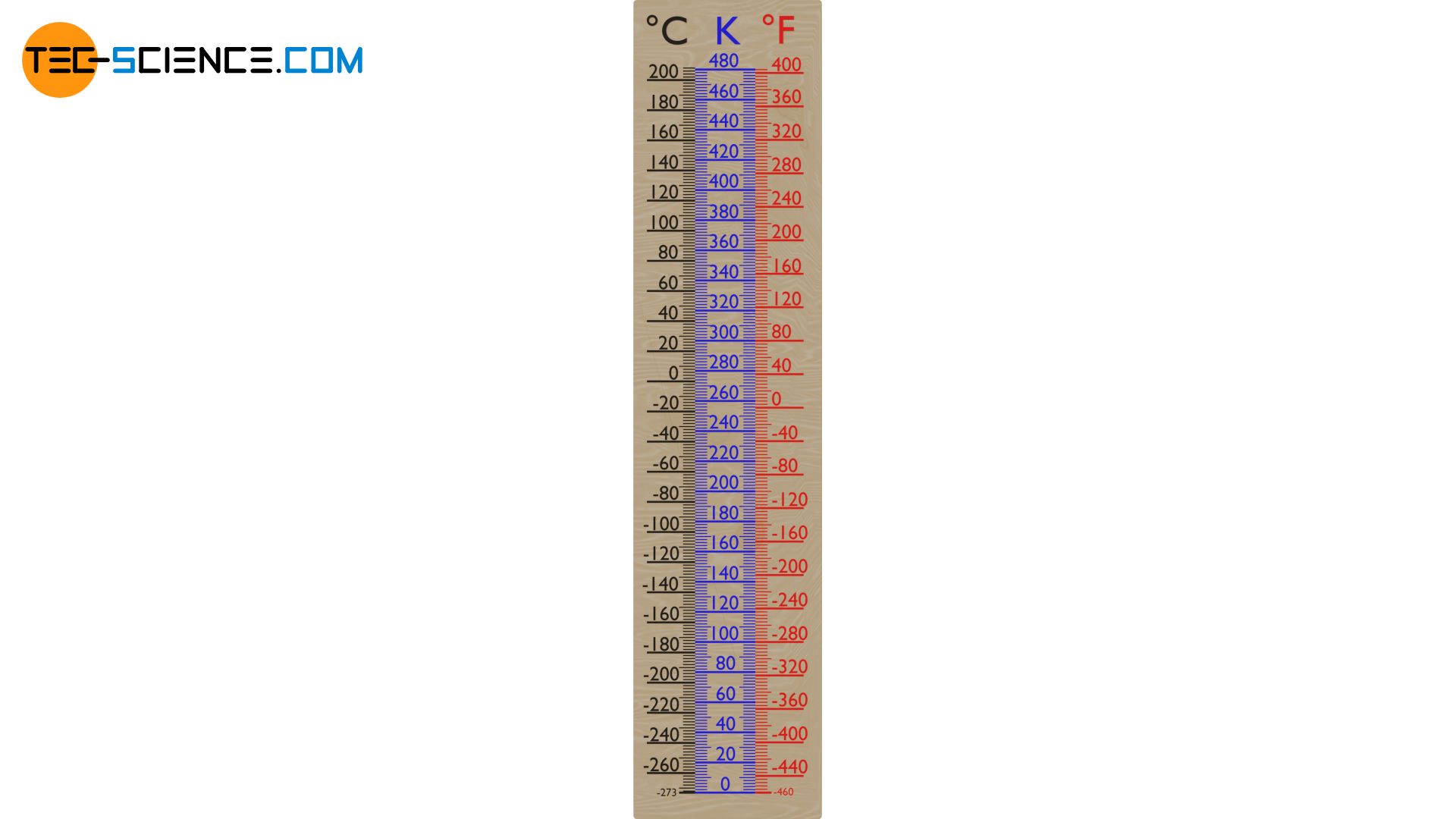
Der absolute Nullpunkt liegt in der Celsius-Skala bei -273,15 °C und dient fortan als Fixpunkt der Kelvinskala. Dem absoluten Nullpunkt wird folglich der Wert 0 K zugeordnet (K: Kelvin). Die Unterteilung der Kelvin-Skala erfolgt wie auch die der Celsius-Skala in insgesamt 100 Schritten zwischen Schmelzpunkt (273 K ≙ 0 °C) und Siedepunkt (373 K ≙ 100 °C) von Wasser.
Der absolute Nullpunkt bezeichnet die Temperatur bei der die Teilchen eines Stoffes keinerlei Bewegungsenergie mehr aufweisen, d.h. völlig in Ruhe sind! Er liegt in der Celsiusskala bei -273,15 °C und in der Fahrenheitskala bei -459,67 °F!
Die Kelvin-Skala ist lediglich eine verschobene Celsius-Skala, mit einem wissenschaftlich festgelegten Temperaturnullpunkt, der sinnvollerweise dem Stillstand der in einem Stoff enthaltenen Teilchen entspricht. Für die Umrechnung eines Temperaturwertes von der Celsius-Skala in den Temperaturwert der Kelvin-Skala und umgekehrt gilt damit:
\begin{align}
&\boxed{ [K] = [°C] + 273,15} \\[5px]
&\boxed{ [°C] = [K] – 273,15} \\[5px]
\end{align}
Für die Umrechnung eines Temperaturwertes von der Fahrenheit-Skala in den Temperaturwert der Kelvin-Skala und umgekehrt gilt:
\begin{align}
&\boxed{ [K] = \frac{[°F] – 32}{1,8} + 273,15} \\[5px]
&\boxed{ [°F] = \left([K] – 273,15\right) \cdot 1,8 + 32 } \\[5px]
\end{align}
Die untere Abbildung zeigt den Vergleich der verschiedenen Temperaturskalen.
Experimentelle Bestimmung des absoluten Nullpunktes
Im Alltag ist es nur bedingt möglich Stoffe so stark abzukühlen, dass hierdurch der absolute Nullpunkt direkt ermittelt werden könnte. Zudem sind die atomaren Teilchen nicht direkt sichtbar, um beurteilen zu können ob der Bewegungsnullpunkt auch tatsächlich erreicht worden ist. In diesem Abschnitt soll deshalb eine Vorgehensweise zur Bestimmung des absoluten Nullpunktes gezeigt werden, die dann zur Einführung der Kelvin-Skala führt.
Um den Bewegungsnullpunkt der Teilchen und damit den absoluten Temperaturnullpunkt ohne größeren Aufwand experimentell zu ermitteln, werden zunächst folgende Vorüberlegungen angestellt:
- Soll die Temperatur ein Maß für die Geschwindigkeit der Teilchen in einem Stoff darstellen, so muss es folglich einen tiefsten Temperaturpunkt geben, in dem die Teilchen keine Geschwindigkeit besitzen.
- Für ein reales Gas würde dies bedeuten, dass alle Gasteilchen auf ein kleinstmögliches Volumen zusammen fallen, da keinerlei Teilchenbewegung vorhanden ist.
- Für ein ideales Gas, dessen Teilchen als Massenpunkte ohne räumliche Ausdehnung angenommen werden, wäre das Volumen in diesem tiefst möglichen Temperaturpunkt folglich Null.
Demzufolge kann man den Absoluten Nullpunkt also dadurch ermitteln, dass man die Gesetzmäßigkeiten zwischen Temperatur und Volumen für ein (näherungsweise) ideales Gas genauer untersucht und anschließend die Temperatur bestimmt bei der das Volumen theoretisch unendlich klein werden müsste.

Versuchsaufbau
Einem idealen Gas am nächsten kommt Helium, weshalb es sinnvoll ist das Temperatur-Volumen-Verhalten von Helium näher zu untersuchen. Die Untersuchung dieses Temperatur-Volumen-Zusammenhangs kann mit einem Glasröhrchen erfolgen, innerhalb dessen sich Helium (oder im einfachsten Fall Luft) befindet.
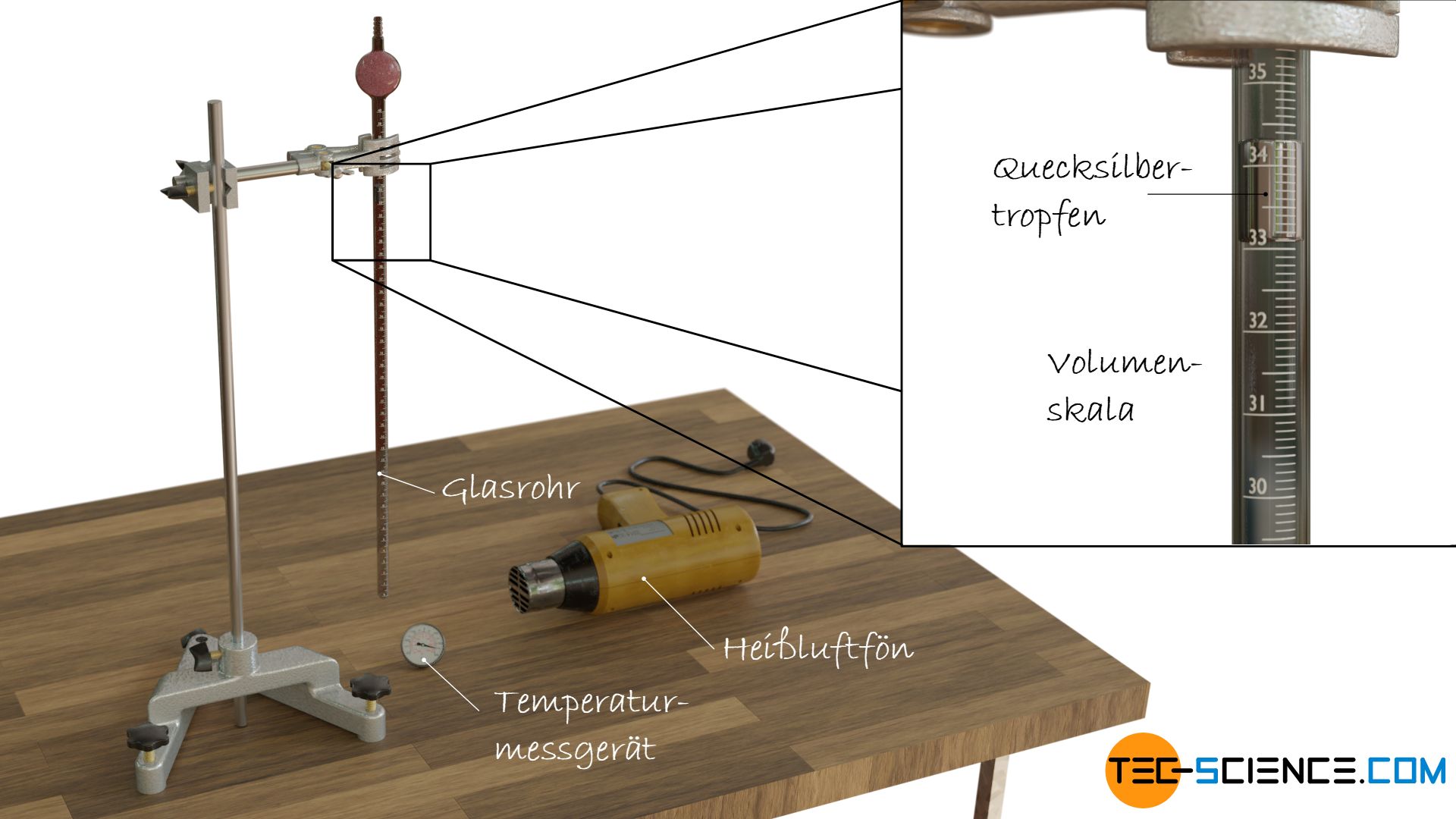
Damit das Gas nicht entweicht, sich gleichzeitig jedoch ausdehnen und zusammenziehen kann, ist das Glasröhrchen mit einem Tropfen aus Quecksilber verschlossen. Das Gasvolumen kann sich bei gleichbleibendem Umgebungsdruck somit stets der vorgegebenen Temperatur anpassen. Die verschiedenen Temperaturen können mit einem Heißluftfön gezielt eingestellt werden. Das Volumen welches das Gas bei einer bestimmten Temperatur einnimmt wird direkt an einer Skala am Glasröhrchen abgelesen.

Bei diesem Versuch ist es sinnvoll das Gas zunächst maximal zu erwärmen und die Temperatur-Volumen-Messwerte erst während des Abkühlvorgangs zu erfassen, da das Abkühlen deutlich gleichmäßiger erfolgt als das punktuelle Aufwärmen mit einem Heißluftfön. Somit ist sichergestellt, dass das gesamte Gas eine einheitliche Temperatur aufweist und nicht nur stellenweise heiß wird.
Versuchsauswertung
Führt man nun den Versuch für verschiedene Temperaturen durch und stellt den sich ergebenden Temperatur-Volumen-Zusammenhang graphisch dar, so zeigt sich ein linearer Zusammenhang. Dies bedeutet, dass sich das Volumen bei einer Temperaturerhöhung kontinuierlich vergrößert und bei einer Temperaturerniedrigung entsprechend gleichmäßig verkleinert. Mithilfe dieser Gesetzmäßigkeit kann nun eine Vorhersage getroffen werden, welche tiefst mögliche Temperatur bei einem unendlich kleinen Volumen zu erwarten ist.
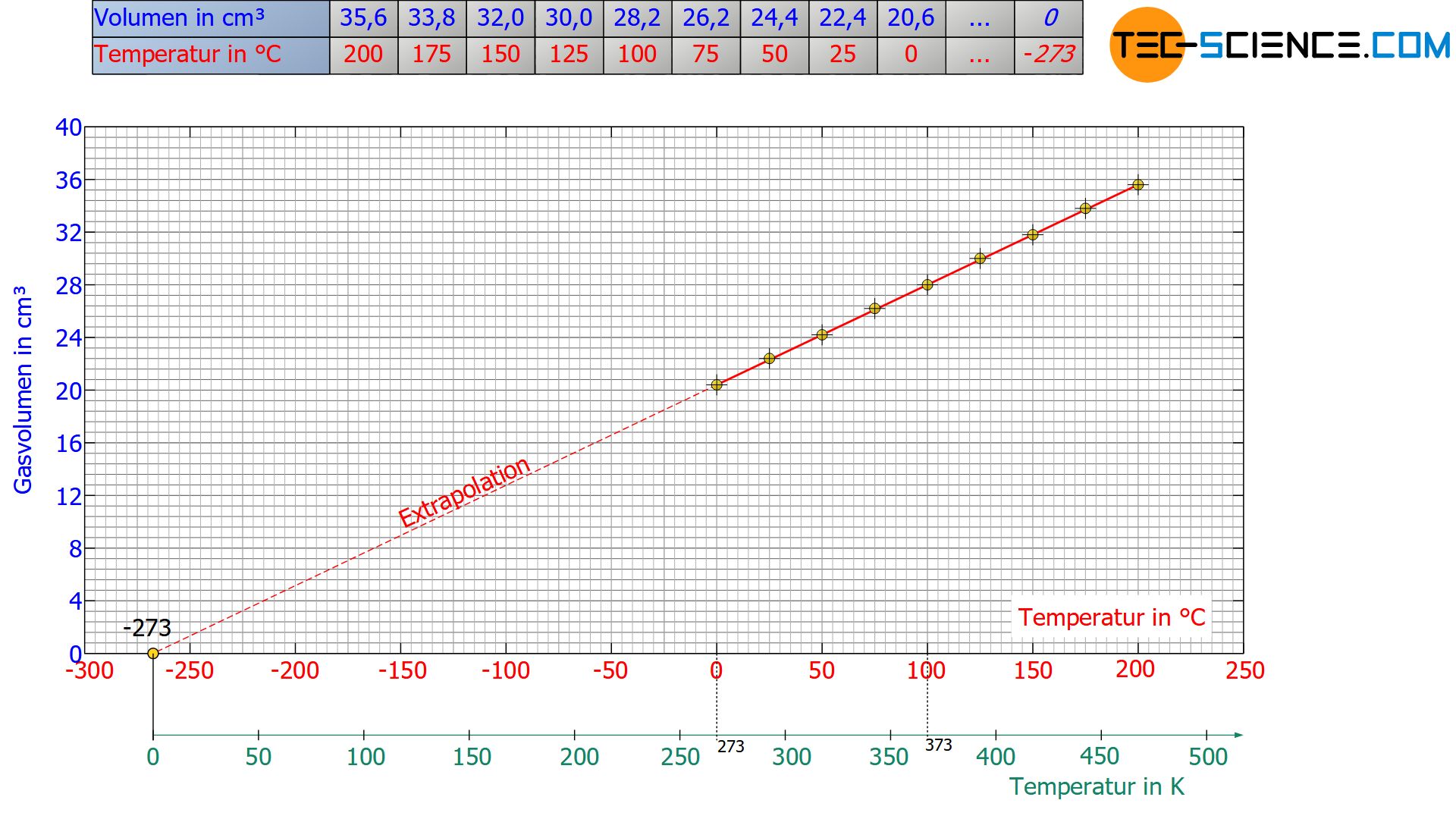
Hierzu wird die Gerade im Diagramm für immer kleiner werdende Volumina fortgesetzt (extrapoliert) bis schließlich beim Schnittpunkt mit der Temperaturachse das kleinstmögliche Volumen von Null erreicht ist. Folglich entspricht also jener Schnittpunkt mit der Temperaturachse dem Absoluten Nullpunkt. Dieser Nullpunkt liegt in der Celsiusskala bei -273,15 °C und in der Fahrenheitskala bei -459,67 °F.
Beachte, dass sich auch bei der Verwendung von anderen Gasarten immer wieder dieser Temperatur-Nullpunkt ergeben wird. Aus diesem Grund bezeichnet man diesen Temperaturwert als Absoluten Nullpunkt, der unabhängig der Stoffart für alle Stoffe gleichermaßen gilt.
Anmerkung: Als Extrapolation bezeichnet man die Ermittlung eines Wertes, der außerhalb eines gemessenen Bereiches liegt. Hierbei wird ohne gesicherte Erkenntnis angenommen, dass die geltenden Gesetzmäßigkeiten innerhalb des gesicherten Bereichs der gemessenen Werte auch auf Werte außerhalb übertragbar sind. Inwieweit dies zulässig ist, muss jedoch gesondert überprüft werden! Als Interpolation bezeichnet man hingegen die Bestimmung eines Wertes innerhalb eines gemessenen Bereichs, der nicht direkt gemessen wurde. Interpolation meint also die Bestimmung eines Wertes zwischen (lat. „inter“) zwei gesicherten Werten.