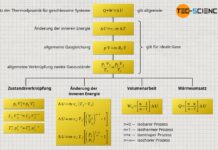
Das Gesetz von Boyle-Mariotte beschreibt die Zunahme des Druck bei abnehmendem Volumen für eine Zustandsänderung bei konstanter Temperatur (isothermer Prozess).
Isotherme Zustandsänderung
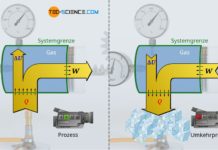
Erfolgen thermodynamische Prozesse bei konstanter Temperatur, so werden diese als isotherme Zustandsänderungen bezeichnet. Das langsame Zusammenpressen einer Luftpumpe bei geschlossenem Auslassventil stellt bspw. eine solche (quasi-)isotherme Zustandsänderung dar.

Das Zusammendrücken der Luftpumpe sollte deshalb langsam erfolgen, weil sich somit eine eventuelle Erwärmung rasch durch das Gehäuse ausgleichen kann und es nicht zu einer Temperaturänderung kommt. Komprimiert man die Luft allerdings relativ schnell und wiederholt dies oft hintereinander (so wie normalerweise üblich beim Benutzen einer Luftpumpe), dann stellt man in der Praxis eine deutliche Erwärmung der Pumpe fest. Dies muss vermieden werden, wenn es sich um einen isothermen Prozess handeln soll.
Grundsätzlich stellt man beim Komprimieren der Luft fest, dass mit kleiner werdendem Volumen ein entsprechender Druckanstieg verbunden ist. Die genauere Abhängigkeit des Gasdrucks vom Volumen während einer isothermen Zustandsänderung eines geschlossenen Systems soll im Folgenden näher untersucht werden.
Experimentelle Untersuchung
Versuchsaufbau
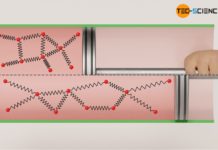
Zur Untersuchung der Zusammenhänge wird ein Glaszylinder verwendet, der mit einem beweglichen Kolben verschlossen ist. Am Glaszylinder ist ein Druckmesser angeschlossen. Als Gas wird Luft verwendet, das näherungsweise als ideales Gas betrachtet werden kann. Das Gasvolumen kann durch die Kolbenstellung variiert werden. Der genaue Wert des Volumens ist auf der angebrachten Skala ablesbar. Der je nach eingestelltem Volumen resultierende Druck, wird am Druckmesser abgelesen. Auf diese Weise kann die Abhängigkeit des Druck (als Absolutdruck!) vom Volumen bei konstanter Temperatur untersucht werden.

Während des Verschiebens des Kolbens zur Einstellung der unterschiedlichen Volumina ist auf eine langsame Zustandsänderung zu achten, sodass sich die enthaltene Luft nicht erwärmt. Prinzipiell lässt sich eine leichte Erwärmung während der Zustandsänderung nicht vermeiden. Deshalb sollte nach Verändern der Kolbenstellung stets eine hinreichend lange Zeit abgewartet werden, bevor die Messwerte notiert werden. Auf diese Weise können sich Temperaturänderung wieder ausgleichen und die Zustandsänderung weiterhin als isotherm betrachtet werden.
Auswertung
Bereits während des Versuchs stellt man fest, dass der Druck umso größer ist, je kleiner das Volumen wird. Eine genauere Analyse zeigt, dass eine Halbierung des Volumens, eine Verdopplung des Drucks zur Folge hat. Beträgt das Volumen nur noch ein Drittel des ursprünglichen Wertes, dann hat sich der Druck sogar verdreifacht. Bei einem Viertel des Volumens, ist der Druck bereits auf das Vierfache angestiegen. Man sagt hierzu auch, dass sich Volumen und Druck umgekehrt proportional zueinander verhalten:
\begin{align}
&\boxed{p \sim \frac{1}{V}} ~~~\text{isotherme Zustandsänderung eines geschlossenen Systems} \\[5px]
\end{align}
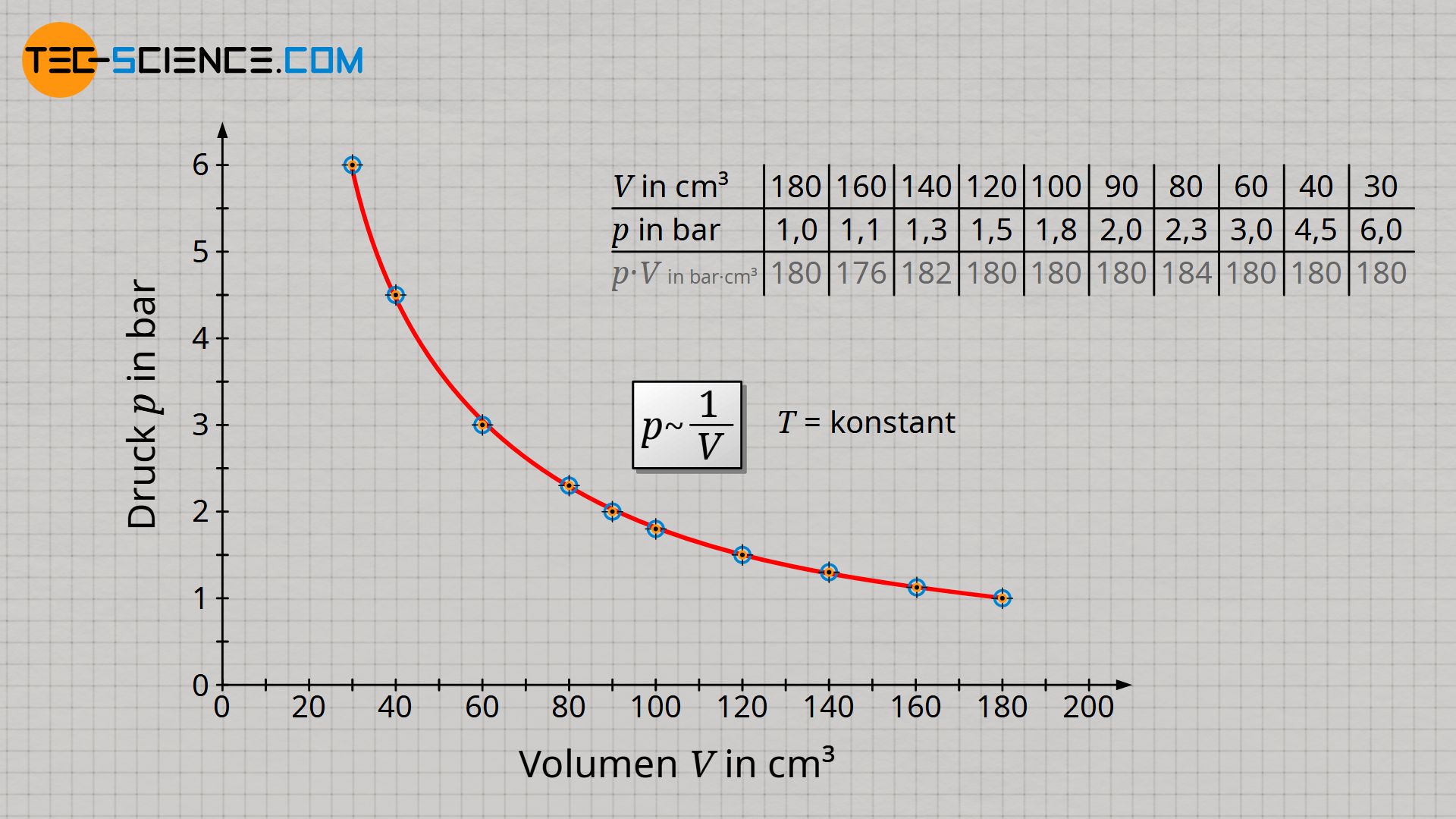
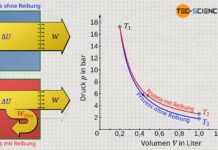
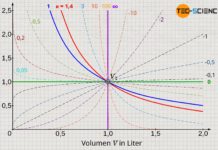
Wird die Messreihe in einem Volumen-Druck-Diagramm veranschaulicht, dann ergibt sich in diesem Fall eine sogenannte Hyperbel als mathematischer Zusammenhang beider Größen.
Folgerung
Wenn sich bei einem umgekehrt proportionalem Verhalten zweier Größen, die eine Größe im selben Maße vergrößert wie sich die andere Größe verringert, dann ist das Produkt aus beiden Größe offenbar stets konstant. Dies Aussage kann auch anhand der Wertetabelle rasch verifiziert werden (Abweichungen kommen durch Messunsicherheiten in der Ablesung des Drucks zustande). Für eine isotherme Zustandsänderung ist das Produkt aus Druck und Volumen folglich stets konstant:
| Volumen V (in cm³) | 180 | 160 | 140 | 120 | 100 | 90 | 80 | 60 | 40 | 30 |
| Druck p (in bar) | 1,0 | 1,1 | 1,3 | 1,5 | 1,8 | 2,0 | 2,3 | 3,0 | 4,5 | 6,0 |
| p⋅V (in bar⋅cm³) | 180 | 176 | 182 | 180 | 180 | 180 | 184 | 180 | 180 | 180 |
\begin{align}
&\boxed{p \cdot V = \text{konstant}}~~~~~\text{Gesetz von Boyle-Mariotte} \\[5px]
\end{align}
Die Konstanz des Produktes von Druck und Volumen bei einem isothermen Prozess wurde von den Physikern Robert Boyle und Edme Mariotte experimentell untersucht. Deshalb ist diese Gesetzmäßigkeit auch als Boyle-Mariotte’sches Gesetz bekannt.
Das Gesetz von Boyle-Mariotte besagt, dass bei einer isothermen Zustandsänderung eines geschlossenen Systems, das Produkt von Druck und Volumen konstant ist!
Verknüpfung zweier Zustände
Bei einem isothermen Prozess hat also das Produkt aus Druck und Volumen für alle Gaszustände denselben konstanten Wert. Deshalb gilt insbesondere, dass das Produkt aus Druck und Volumen in einem beliebigen (Anfangs-)Zustand 1 auch dem Produkt aus Druck und Volumen in einem beliebigen (End-)Zustand 2 entspricht:
\begin{align}
&p_1 \cdot V_1 = \text{konstant}= p_2 \cdot V_2 \\[5px]
&\boxed{p_1 \cdot V_1 = p_2 \cdot V_2} \\[5px]
\end{align}

Bei einer isothermen Zustandsänderung eines geschlossenen Systems, stehen zwei Zustände über das Produkt von Druck und Volumen in Zusammenhang!
Zusammenhang zum idealen Gasgesetz
Der oben gezeigte Zusammenhang zwischen zwei Gaszuständen ergibt sich auch aus dem idealen Gasgesetz für den Spezialfall einer Zustandsänderung bei konstanter Temperatur (T1=T2):
\begin{align}
\require{cancel}
&\frac{p_1 \cdot V_1}{\cancel{T_1}} = \frac{p_2 \cdot V_2}{\cancel{T_2}} \\[5px]
&\boxed{p_1 \cdot V_1 = p_2 \cdot V_2 } \\[5px]
\end{align}
Die Konstanz des Produktes aus Druck und Volumen ergibt sich auch direkt anhand der thermischen Zustandsgleichung. Für den Fall, dass sich die Temperatur nicht ändert (T=konstant) und das System geschlossen ist (m=konstant) gilt:
\begin{align}
&p \cdot V = \underbrace{R_\text{s} \cdot m \cdot T}_{=\text{konstant}} ~~~~~\text{thermische Zustandsgleichung}\\[5px]
&\boxed{p \cdot V =\text{konstant}} \\[5px]
\end{align}