Druck und Temperatur (kinetische Gastheorie)

Erfahre in diesem Artikel mehr über den Zusammenhang zwischen Druck und Temperatur vor dem Hintergrund der kinetischen Gastheorie.

Einleitung

Um die makroskopisch zu beobachteten Zustandsgrößen eines Gases wie Temperatur, Volumen und Druck mit den mikroskopischen Größen wie Teilchenmasse und Teilchengeschwindigkeit zu verknüpfen, wurde die kinetische Gastheorie entwickelt. Mit ihrer Hilfe ist es bspw. möglich aus der mittleren kinetischen Energie der Gasteilchen auf die Temperatur zu schließen oder auch auf den Gasdruck.

Die kinetische Gastheorie liefert für (ideale) Gase wichtige Zusammenhänge zwischen makroskopisch messbaren Zustandsgrößen (z.B. Temperatur, Druck, Volumen, Gasmasse, etc.) und mikroskopischen Größen (z.B. Teilchengeschwindigkeit, mittlere kinetische Energie, Teilchenanzahl, Teilchemasse, etc.)!

Annahmen

Um ein Modell über das Verhalten von Gasteilchen zu entwickeln, müssen zunächst einige Annahmen über die Eigenschaften von Gasen bzw. den darin enthaltenen Teilchen getroffen werden. Zunächst wird davon ausgegangen, dass es sich bei den Gasen um ideale Gase handelt. Dies bedeutet insbesondere:

1. die Gasteilchen werden als Massepunkte betrachtet,
2. die Gasteilchen üben keinerlei Bindungskräfte untereinander aus,
3. es treten bei Kollisionen zwischen den Gasteilchen nur elastische Stöße auf (d.h. kein Energieverlust)
4. ebenfalls werden Stöße zwischen Gasteilchen und Grenzflächen (wie bspw. Gefäßwände) als vollkommen elastisch betrachtet,
5. alle Gasteilchen bewegen sich völlig regellos, d.h. sie haben keine Vorzugsrichtung und sind deshalb statistisch („gleichmäßig“) im Raum verteilt (d.h. der Einfluss der Gravitation auf die Gasteilchen wird vernachlässigt).

Mikroskopische Interpretation des Gasdrucks

Zustandekommen des Gasdrucks

Im Artikel „Gasdruck“ wurde mithilfe des Teilchenmodells bereits ausführlich das Zustandekommen des Gasdrucks erläutert. So kann der makroskopisch messbare Gasdrucks („Kraft pro Fläche“) auf mikroskopischer Ebene durch Stoßprozess erklärt werden. Prallen nämlich die Gasteilchen auf eine Grenzfläche, dann üben sie Kräfte aus – analog zu Tennisbällen, die gegen einen Schläger geworfen werden.

Die Druckwirkung in Gasen kommt auf mikroskopischer Ebene durch Stoßprozesse der darin enthaltenen Teilchen zustande, die auf angrenzende Flächen prallen und somit Stoßkräfte ausüben!

Ist bspw. ein unter hohem Druck stehendes Gas in einem Zylinder eingeschlossen, dann prallen die darin enthaltenen Teilchen ständig mit der Zylinderwand zusammen und üben Kräfte aus. Diese Stoßkräfte lassen sich deutlich spüren, wenn man bspw. den Zylinder mit einem beweglichen Kolben verschließt.

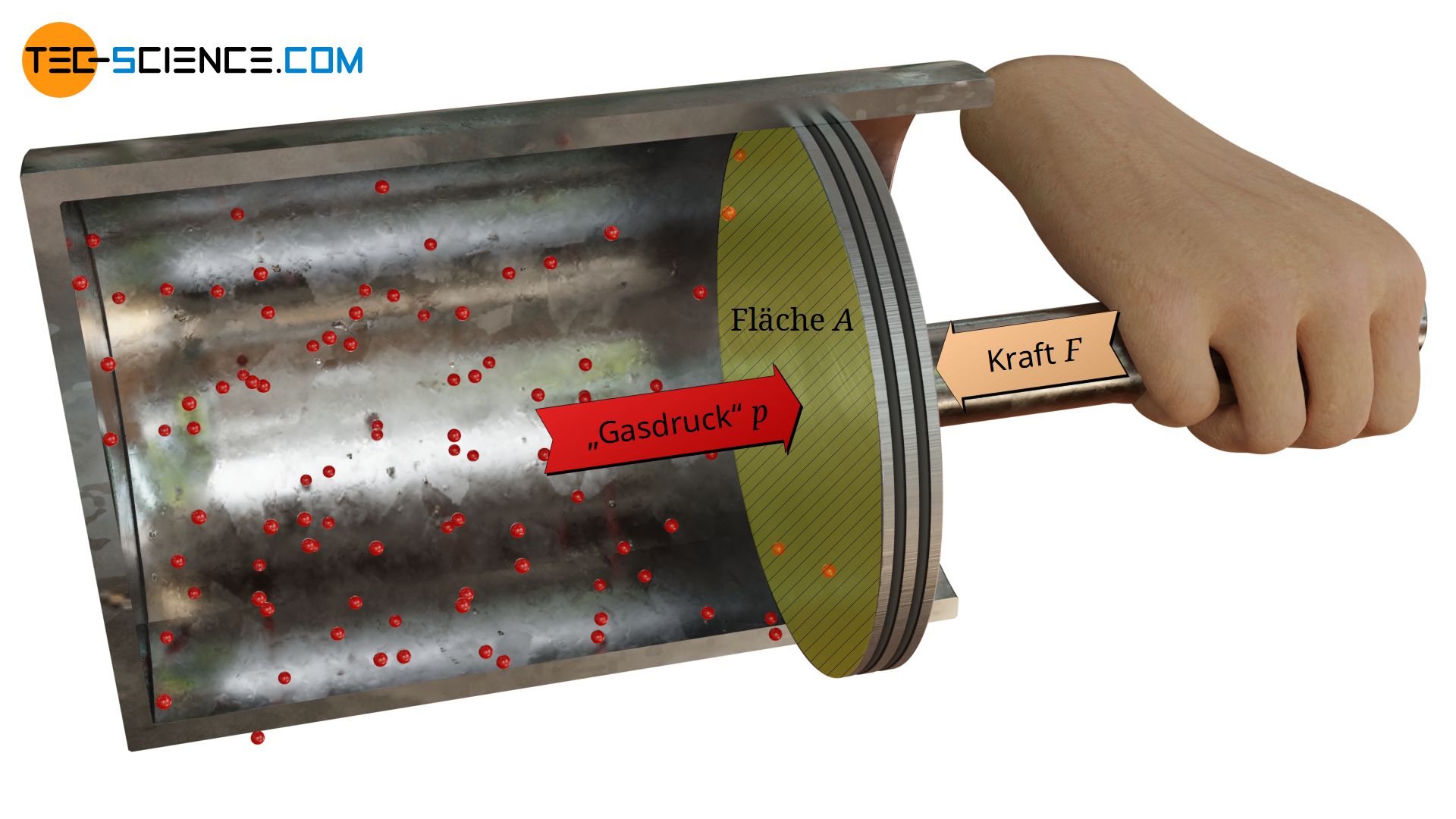
Die untere Animation zeigt hierzu schematisch die Stoßprozesse zwischen Gasteilchen und Kolbenfläche. Anders als in der Animation dargestellt, wird man aufgrund der Vielzahl an Teilchen die ein Gas normalerweise enthält, hingegen kein einzelnes „hämmern“ der Teilchen verspüren sondern eine konstante Kraft wahrnehmen.

Die Kraft F, die in diesem Zustand benötigt wird um den Kolben in Stellung zu halten, ist alleine Kollisionen zwischen Gasteilchen und Kolbenfläche A geschuldet, d.h. dem Gasdruck! Aus der allgemeinen Definition des Drucks („Kraft pro Fläche“) lässt sich der Gasdruck p schließlich wie folgt ermitteln:

\begin{align}
\label{p}
&\boxed{p = \frac{F}{A}} \\[5px]
\end{align}

Anmerkung: Nicht nur die Gasteilchen im Inneren des Zylinders prallen auf die Kolbenfläche und üben somit einen nach außen gerichtete Kraft aus. Auch die umgebende Luft außerhalb des Zylinders beinhaltet Teilchen. Diese üben deshalb zusätzlich eine entgegengesetzte Kraft auf den Kolben aus, die nach innen gerichtet ist. Erst die Differenz beider Kräfte entspricht jener Kraft die benötigt wird, um den Kolben in Stellung zu halten. Der Einfachheit halber wird deshalb im Folgenden von einem Vakuum außerhalb des Zylinders ausgegangen, sodass die Kraft F in Gleichung (\ref{p}) dann tatsächlich alleine den Gasteilchen im Inneren des Zylinders geschuldet ist und der Gasdruck auf diese Weise entsprechend ermittelt werden kann.

Einflussgrößen auf den Gasdruck

Der Gasdruck wird im Zylinder wird umso größer sein, je mehr Teilchen innerhalb einer gewissen Zeit auf die Kolbenfläche prallen. Dies hängt zum einen von der Anzahl der Teilchen ab, die sich im Zylindervolumen befinden. Denn je mehr Teilchen insgesamt vorhanden sind, desto mehr können auch auf die Kolbenfläche prallen und werden (Stoß-)Kräfte ausüben. Dies zeigt auch bereits die alltägliche Erfahrung beim Aufpumpen eines Fahrradreifens: Je mehr Luft in den Reifen gepumpt wird (d.h. je mehr Teilchen enthalten sind), desto größer ist der Druck!

Zum anderen hängt der Gasdruck von der Geschwindigkeit ab, mit der die Teilchen auf die Kolbenfläche prallen. Denn umso größer die Geschwindigkeit, desto heftiger sind die Kollisionen mit der Kolbenfläche und umso größer die Stoßkräfte bzw. der damit verbundene Druck. Auch dies zeigt bereits die alltäglich Erfahrung: Wird eine mit Luft gefüllte Flasche in die Sonne gestellt, dann wird der Druck in der Flasche mit steigender Temperatur zunehmen, da mit höherer Temperatur die Geschwindigkeit der Teilchen zunimmt.

Berechnung des Gasdrucks

Um den Druck im Zylinder zu bestimmen, muss also zunächst die Anzahl der Teilchen ermittelt werden, die innerhalb einer gewissen Zeit Δt auf die Kolbenfläche prallen. Grundsätzlich können dabei nur jene Teilchen auf den Kolben treffen, die zum einen auch tatsächlich in Richtung Kolben fliegen und zum anderen auch nahe genug an der Kolbenfläche sind.

Im Allgemeinen besteht die Geschwindigkeit eines Teilchens aus drei Komponenten (x-, y- und z-Komponente), wobei für das Zustandekommen des Drucks nur die Geschwindigkeistkomponente relevant ist mit der das Teilchen auf die Kolbenfläche trifft, d.h. die Geschwindigkeit in x-Richtung.

Zunächst wird vereinfachend davon ausgegangen, dass die x-Komponente der Geschwindigkeit für alle Teilchen betragsmäßig identisch ist (|v_x|). Da keine Richtung speziell von den Teilchen bevorzugt wird, wird sich auch die Hälfte aller Teilchen mit dieser Geschwindigkeit |v_x| in positive x-Richtung bewegen und die andere Hälfte in negative x-Richtung.

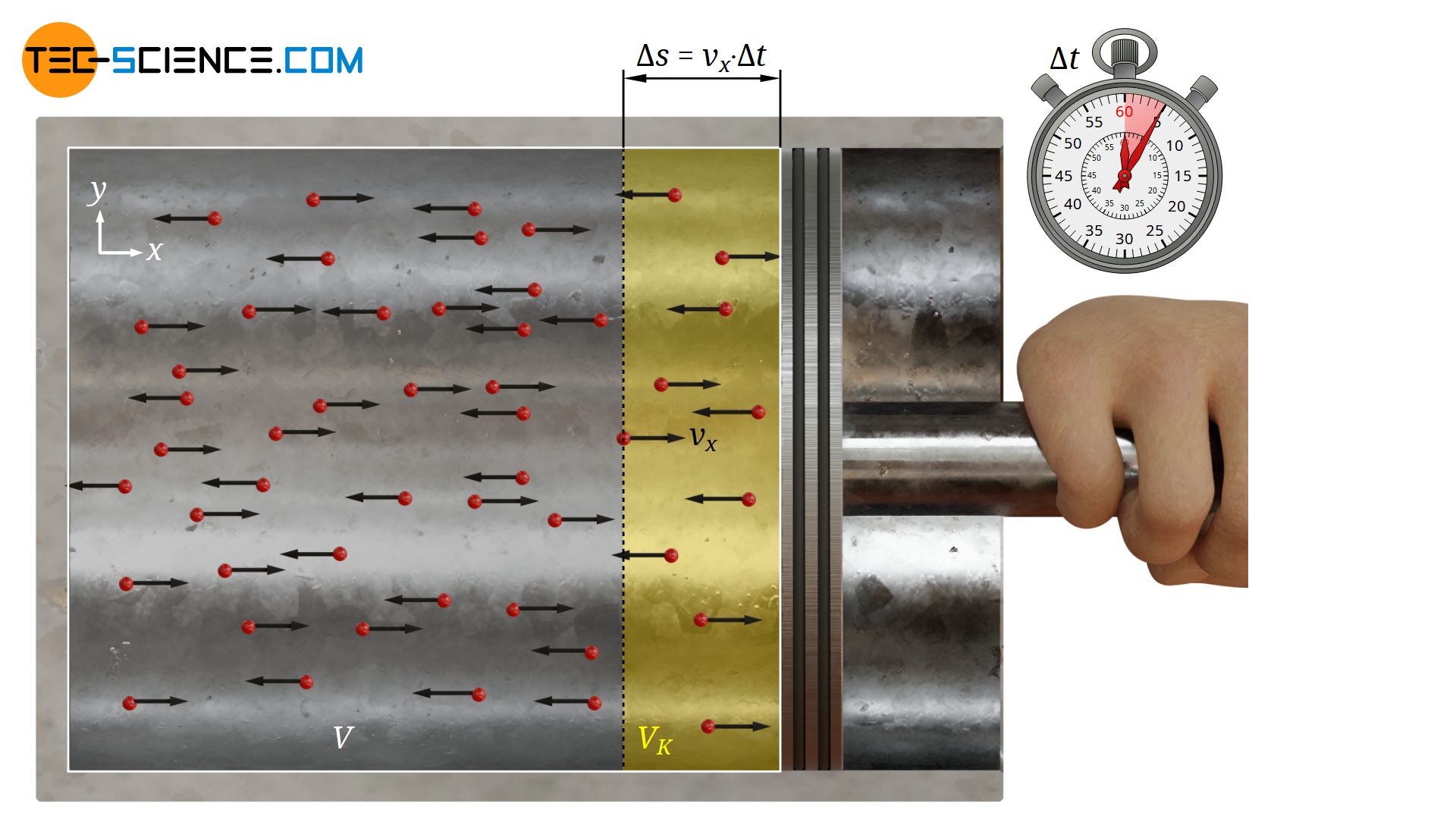
Dabei können aber nicht alle Teilchen die in positive Richtung fliegen auch tatsächlich die Kolbenfläche innerhalb der gegebenen Zeit Δt erreichen. Schließlich können die Teilchen mit der als konstant vorausgesetzten Geschwindigkeit |v_x| innerhalb der Zeit Δt maximal eine Strecke Δs zurücklegen:

\begin{align}
&\Delta s = |v_x| \cdot \Delta t \\[5px]
\end{align}

Dies bedeutet umgekehrt, dass nur Teilchen auf die Kolbenfläche prallen können, die weniger als Δs vom Kolben entfernt sind (siehe gelb markiertes Volumen V_K in der oberen Abbildung). Alle anderen Teilchen werden schlichtweg nicht die Zeit haben den Kolben innerhalb der Zeit Δt zu erreichen.

Da die Teilchen gleichmäßig im Zylinder verteilt sind, kann aus der Teilchendichte im Zylinder N/V (Verhältnis von Gesamtteilchenanzahl N und Gesamtzylindervolumen V), die im relevanten Kollisionsvolumen V_K enthaltene Teilchenanzahl N_K wie folgt ermittelt werden:

\begin{align}
&N_K = \frac{N}{V} \cdot V_K \\[5px]
\end{align}

Nun muss noch berücksichtigt werden, dass sich nur die Hälfte der im Kollisionsvolumen befindlichen Teilchen auch tatsächlich in positive x-Richtung auf den Kolben zubewegt. Für die Anzahl der Teilchen N_x im Kollisionsvolumen, die tatsächlich in Richtung Kolben fliegt, gilt folglich:

\begin{align}
&N_x = \frac{1}{2} \cdot N_K = \frac{1}{2} \cdot \frac{N}{V} \cdot V_K \\[5px]
\end{align}

Das für die Entstehung des Drucks relevante Kollisionsvolumen V_K ergibt sich aus dem Produkt von Kolbenfläche A und Strecke Δs. Somit gilt für die relevante Teilchenanzahl N_x im Stoßbereich:

\begin{align}
&N_x = \frac{1}{2} \cdot \frac{N}{V} \cdot \overbrace{A \cdot \Delta s}^{V_K} = \frac{1}{2} \cdot \frac{N}{V} \cdot A \cdot \overbrace{|v_x| \cdot \Delta t}^{\Delta s} \\[5px]
\end{align}

Jedes der insgesamt N_x Teilchen wird bei der Kollision mit dem Kolben seinen Impuls um einen bestimmten Betrag |Δp| ändern. Die gesamte Impulsänderung |Δp_ges| aller Teilchen über die betrachtete Zeitdauer Δt hinweg, entspricht dem Kraftbetrag |F_ges| den die Teilchen insgesamt auf die Kolbenfläche ausüben („Kraftstoß“):

\begin{align}
\require{cancel}
\label{force}
&|F_{ges}| = \frac{|\Delta p_{ges}|}{\Delta t} = \frac{N_x \cdot |\Delta p|}{\Delta t} = \frac{\frac{1}{2} \cdot \frac{N}{V} \cdot A \cdot |v_x| \cdot \bcancel{\Delta t} \cdot |\Delta p|}{\bcancel{\Delta t}} = \frac{1}{2} \cdot \frac{N}{V} \cdot A \cdot |v_x|\cdot |\Delta p| \\[5px]
\end{align}

Eine offensichtliche Erkenntnis aus dem Alltag zeigt sich an dieser Stelle bereits: Die Kraft die die Teilchen auf die Kolbenfläche ausüben ist nicht von der betrachteten Zeitdauer Δt abhängig! Wäre dies der Fall, dann müsste sich der Druck mit der Zeit ändern. Die Alltagserfahrung zeigt aber, dass der Druck in Gasen konstant bleibt, solange man am Gas selbst keine Änderungen wie eine Temperaturerhöhung oder eine Volumenverkleinerung vornimmt!

Die Impulsänderung |Δp| ist für jedes Teilchen identisch, da vorausgesetzt wurde, dass sich alle Teilchen mit betragsmäßig derselben Geschwindigkeit |v_x| bewegen und es sich bei den Kollision mit dem Kolben nur um elastische Stöße ohne (kinetischen) Energieverlust handelt. Ein Teilchen das sich also mit der Geschwindigkeit |v_x| auf den Kolben zubewegt, wird sich mit betragsmäßig derselben Geschwindigkeit |v_x| wieder in entgegengesetzte Richtung entfernen. Da der Impuls eines Teilchens somit vor dem Stoß +m⋅|v_x| beträgt und nach dem Stoß -m⋅|v_x|, hat sich der Impuls betragsmäßig somit um den doppelten Wert geändert:

\begin{align}
\label{momentum}
&|\Delta p| = 2 \cdot m \cdot |v_x| \\[5px]
\end{align}

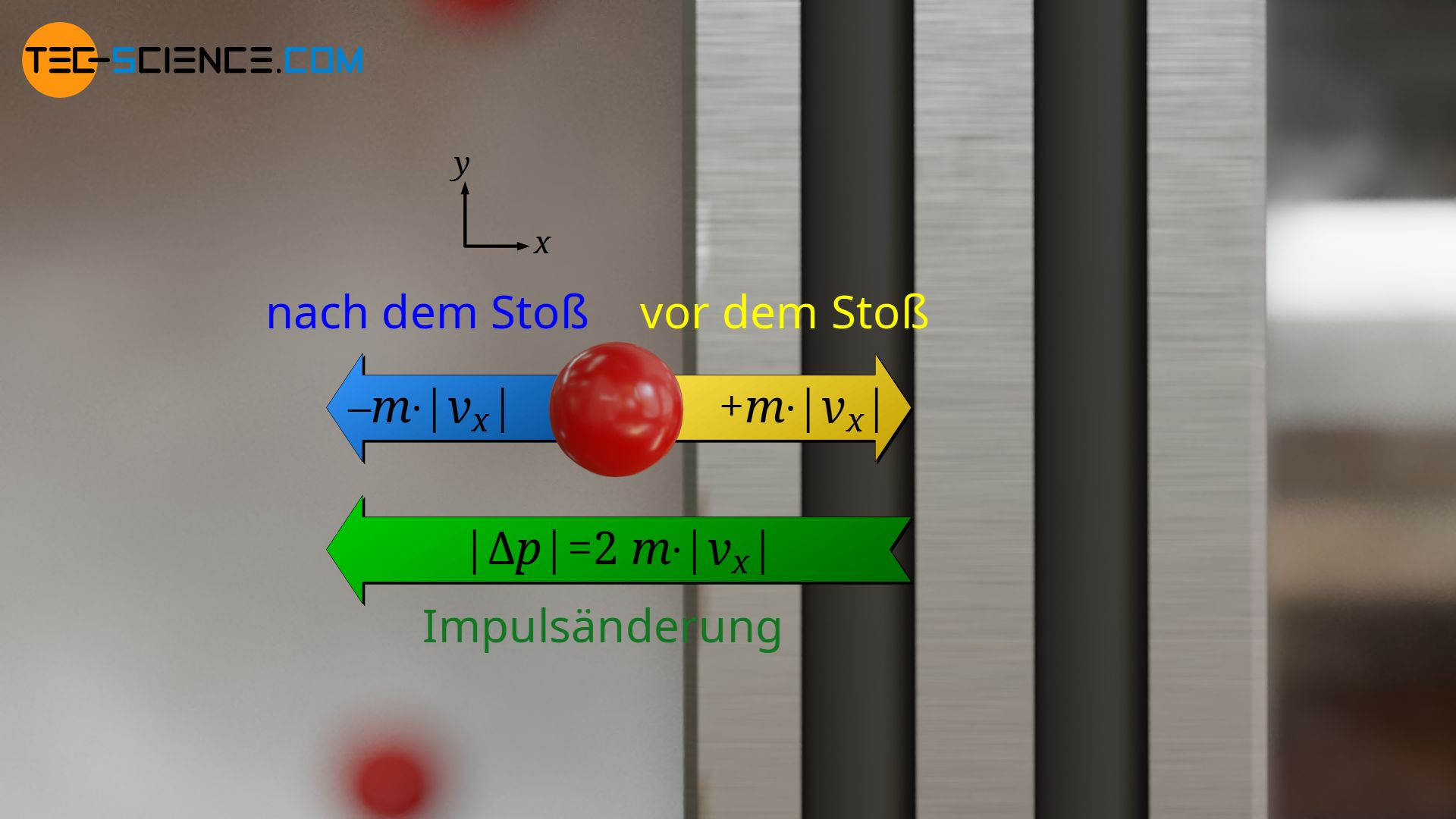
(Analogie: Ändert sich die Temperatur von -20 °C auf + 20°C, dann hat sie sich insgesamt um 40 °C geändert, d.h. betragsmäßig um den doppelten Wert).

Wird Gleichung (\ref{momentum}) nun in Gleichung (\ref{force}) eingesetzt, dann gilt für die Gesamtkraft F_ges die das Gas auf den Kolben ausübt:

\begin{align}
\label{f}
&|F_{ges}| = \frac{1}{2} \cdot \frac{N}{V} \cdot A \cdot |v_x|\cdot \overbrace{2 \cdot m \cdot |v_x|}^{|\Delta p|} =\frac{N}{V} \cdot A \cdot m \cdot |v_x|^2 =\frac{N}{V} \cdot A \cdot m \cdot v_x^2 \\[5px]
\end{align}

Anmerkung: Da die Geschwindigkeit v_x in Gleichung (\ref{f}) quadriert wird, kann auf die Betragsstriche auch verzichtet werden.

Die Kraft |F_ges| wirkt schließlich auf die Kolbenfläche A, sodass sich gemäß Gleichung (\ref{p}) folgender Gasdruck p ergibt:

\begin{align}
\require{cancel}
\label{pp}
& p = \frac{|F_{ges}|}{A} =\frac{\frac{N}{V} \cdot \bcancel{A} \cdot m \cdot v_x^2}{\bcancel{A}} = \frac{N}{V} \cdot m \cdot v_x^2 \\[5px]
\end{align}

Nun muss noch berücksichtigt werden, dass in einem Gas nicht wie ursprünglich angenommen alle Gasteilchen betragsmäßig dieselbe Geschwindigkeitskomponente in x-Richtung aufweisen sondern diese statistisch verteilt ist. Deshalb muss gemäß Gleichung (\ref{pp}) der arithmetische Mittelwert aus den Geschwindigkeitsquadraten gebildet werden:

\begin{align}
\label{ppp}
& \boxed{p =\frac{N}{V} \cdot m \cdot \overline{v_x^2}} \\[5px]
\end{align}

Es darf nicht die Durchschnittsgeschwindigkeit (arithemetisch gemittelte Geschwindigkeit) der Teilchen quadriert werden sondern die einzelnen Geschwindigkeitsquadrate müssen gemittelt werden!

Die untere Tabelle zeigt exemplarisch für 5 Teilchen die Ergebnisse, wenn einmal der Durchschnittswert der Geschwindigkeit quadriert wird und einmal die Geschwindigkeitsquadrate gemittelt werden. So beträgt die Durchschnittsgeschwindigkeit im vorliegenden Fall 3 m/s und das Quadrat hiervon folglich 9 m²/s². Bildet man hingegen den Mittelwert der Geschwindigkeitsquadrate dann erhält man einen Wert von 11,8 m²/s².

Teilchen	Geschwindigkeit v in m/s	Geschwindigkeitsquadrate v² in m²/s²
A	1	1
B	3	9
C	3	9
D	2	4
E	6	36
Arithemtischer Mittelwert	3 m/s	11,8 m²/s²

Beachte, die unterschiedliche Schreibweise zwischen dem Quadrat der mittleren Geschwindigkeit \(\overline{v~}^2\) und dem Mittelwert der Geschwindigkeitsquadrate \(\overline{v^2}\).

Zusammenhang zwischen der Bewegung in x-Richtung und der Gesamtbewegung

Kinematische Betrachtung

Der Betrag der Gesamtgeschwindigkeit v eines Teilchens lässt sich grundsätzlich wie folgt aus den einzelnen Geschwindigkeitskomponenten in x-, y- und z-Richtung ermitteln:

\begin{align}
& v = \sqrt{v_x^2 + v_y^2 + v_z^2}~~~~~\text{Betrag der Geschwindigkeit} \\[5px]
\end{align}

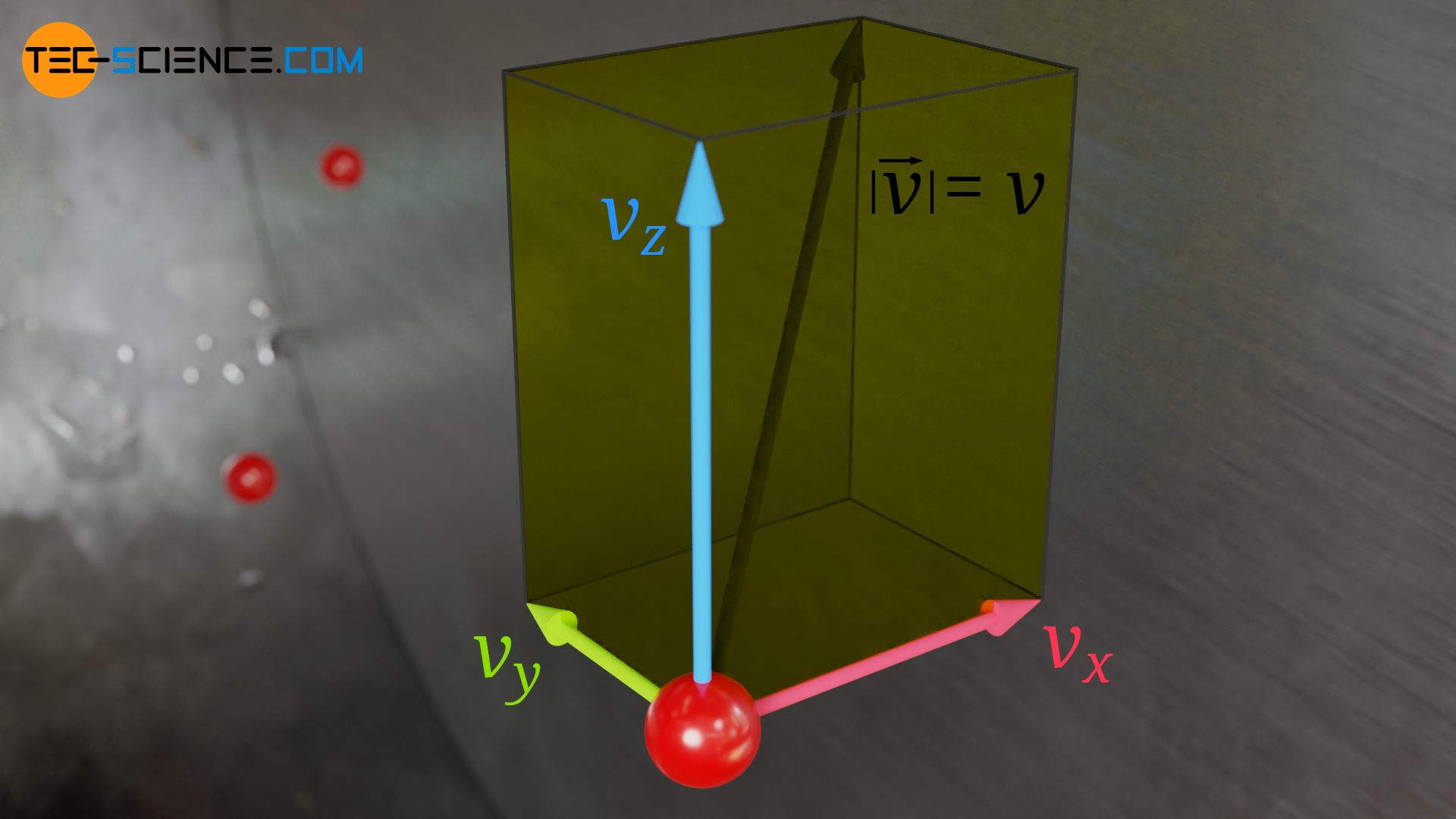
Für das Quadrat der Gesamtgeschwindigkeit v²) gilt folglich:

\begin{align}
& v^2= v_x^2 + v_y^2 + v_z^2 \\[5px]
\end{align}

Natürlich kann dann auch der Mittelwert der quadrierten Gesamtgeschwindigkeit aus dem Mittelwert der einzelnen quadrierten Geschwindigkeitskomponenten ermittelt werden:

\begin{align}
& \overline{v^2}= \overline{v_x^2} + \overline{v_y^2} + \overline{v_z^2} \\[5px]
\end{align}

Die einzelnen Geschwindigkeitskomponenten sind statistisch verteilt und keine Richtung ist bevorzugt. Der Mittelwert der Geschwindigkeitsquadrate wird somit für alle Geschwindigkeitskomponenten identisch sein:

\begin{align}
&\overline{v_x^2} = \overline{v_y^2} = \overline {v_z^2} \\[5px]
\end{align}

Damit zeigt sich folgender Zusammenhang zwischen dem Mittelwert der quadrierten Geschwindigkeiten der Teilchen \(\overline{v^2}\) und dem Mittelwert der quadrierten Geschwindigkeitskomponenten in x-Richtung (\(\overline{v_x^2}\)):

\begin{align}
& \overline{v^2}= \overline{v_x^2} + \overline{v_x^2} + \overline{v_x^2} = 3 \cdot \overline{v_x^2} \\[5px]
\end{align}

Der Mittelwert der quadrierten Geschwindigkeiten in x-Richtung entspricht also einem Drittel der quadrierten Gesamtgeschwindigkeiten der einzelnen Teilchen:

\begin{align}
\label{x}
& \boxed{\overline{v_x^2} = \frac{\overline{v^2}}{3}} \\[5px]
\end{align}

Wird Gleichung (\ref{x}) in Gleichung (\ref{ppp}) eingesetzt, dann zeigt sich folgender Zusammenhang zwischen dem Druck eines Gases p und dem Mittelwert der Geschwindigkeitsquadrate \(\overline{v^2}\) der einzelnen Teilchen:

\begin{align}
\label{yy}
& \boxed{p =\frac{1}{3} \cdot \frac{N}{V} \cdot m \cdot \overline{v^2}} \\[5px]
\end{align}

Beachte, dass sich die Geschwindigkeit v nun nicht mehr nur auf die x-Richtung beschränkt sondern die Gesamtgeschwindigkeit eines Teilchens repräsentiert!

Energetische Betrachtung

Auf dieselben Zusammenhänge wie in Gleichung (\ref{yy}) zum Ausdruck kommt, kommt man auch durch eine energetische Betrachtung. Ausgangspunkt bildet wiederum Gleichung (\ref{ppp}). Wird Gleichung (\ref{ppp}) mit dem Faktor 2 erweitert, dann lässt sich darin der Term \(\frac{1}{2}m \overline{v_x^2}\) als mittlere Bewegungsenergie \(\overline{W_{kin,x}}\) der Teilchen entlang der x-Richtung interpretieren:

\begin{align}
& p =\frac{2}{2} \cdot \frac{N}{V} \cdot m \cdot \overline{v_x^2} =
2 \cdot \frac{N}{V} \cdot \overbrace{\frac{1}{2} m \cdot \overline{v_x^2}}^{\overline{W_{kin,x}}} \\[5px]
\label{druck}
& \boxed{p = 2 \cdot \frac{N}{V} \cdot \overline{W_{kin,x}}} \\[5px]
\end{align}

Da die Geschwindigkeiten statistisch verteilt sind und keine Richtung bevorzugt ist, erhält man in y-Richtung oder z-Richtung letztlich dieselbe Geschwindigkeitsverteilung wie in x-Richtung und damit dieselbe quadratisch gemittelte Geschwindigkeit. Dies wiederum bedeutet, dass die mittlere kinetische Energie der Teilchen in jede Richtung identisch ist (d.h. die mittlere kinetische Energie die sich ergibt wenn man die Bewegung der Teilchen nur entlang einer Raumrichtung betrachten würde):

\begin{align}
& \overline{W_{kin,x}} = \overline{W_{kin,y}} = \overline{W_{kin,z}}\\[5px]
\end{align}

Nun bewegen sich die Teilchen aber nicht nur eine eine Richtung sondern in alle drei Raumrichtungen. Die mittlere kinetische Gesamtenergie \(\overline{W_{kin}}\), die die Teilchen bei ihrer dreidimensionalen Bewegung aufweisen, ergibt sich dann aus der Summe der kinetischen Energien entlang der drei Raumrichtungen. Da die mittleren kinetischen Energie entlang der unterschiedlichen Raumrichtungen jeweils identisch sind, entspricht die Gesamtenergie somit dem dreifachen Wert der kinetischen Energie in eine Raumrichtung (z.B. die in x-Richtung):

\begin{align}
& \overline{W_{kin}} = \overline{W_{kin,x}} + \overline{W_{kin,y}} + \overline{W_{kin,z}} = 3 \cdot \overline{W_{kin,x}} \\[5px]
\label{kine}
&\overline{W_{kin,x}} = \frac{1}{3}\cdot \overline{W_{kin}} \\[5px]
\end{align}

Damit ist der Druck wie folgt mit der mittleren kinetischen Gesamtenergie eines Teilchens verknüpft (einsetzen von Gleichung (\ref{kine}) in (\ref{druck})):

\begin{align}
&p = 2 \cdot \frac{N}{V} \cdot \frac{1}{3} \overline{W_{kin}} \\[5px]
\label{y}
& \boxed{p = \frac{2}{3} \cdot \frac{N}{V} \cdot \overline{W_{kin}}} \\[5px]
\end{align}

Der Druck eines Gases ist neben der Teilchenanzahl und dem Volumen nur von der mittleren kinetischen Energie eines Teilchens abhängig!

Beachte, dass sich die mittlere kinetische Energie eines Teilchens nur auf die translatorische Bewegung bezieht. Die Teilchen eines Gases weisen im Allgemeinen zwar auch eine Rotationsbewegung auf (Rotationsenergie), diese hat jedoch keine Auswirkung auf den Druck!

Da die mittlere kinetische Energie der Teilchen über deren Masse mit der entsprechenden quadratisch gemittelten Geschwindigkeit verknüpft ist (\(\overline{W_{kin}}=\frac{1}{2}m\cdot \overline{v^2}\)), wobei sich die Geschwindigkeit v nun nicht mehr nur auf eine Raumrichtung bezieht sondern auf die Gesamtgeschwindigkeit, dann zeigt sich derselbe Zusammenhang wie in Gleichung (\ref{yy}):

\begin{align}
& p = \frac{2}{3} \cdot \frac{N}{V} \cdot \overbrace{\overline{W_{kin}}}^{\frac{1}{2}m \overline{v^2}} \\[5px]
& \boxed{p =\frac{1}{3} \cdot \frac{N}{V} \cdot m \cdot \overline{v^2}} \\[5px]
\end{align}

Mikroskopische Interpretation der Temperatur

Im Artikel Thermische Zustandsgleichung idealer Gase wurde die allgemeine Gasgleichung auf experimentellem Wege in folgender Form hergeleitet:

\begin{align}
\label{1}
& p \cdot V = N \cdot k_B \cdot T \\[5px]
\end{align}

Darin entspricht k_B der sogenannten Boltzmann-Konstante und T die Temperatur des Gases. Bringt man nun in Gleichung (\ref{y}) das Gasvolumen V auf die linke Seite…

\begin{align}
\label{2}
& p \cdot V =\frac{2}{3} \cdot N \cdot \overline{W_{kin}} \\[5px]
\end{align}

… und setzt dann Gleichung (\ref{1}) und (\ref{2}) gleich, dann zeigt sich der direkte Zusammenhang zwischen der mittleren kinetischen Energie eines Teilchens und der Temperatur:

\begin{align}
\require{cancel}
& \frac{2}{3} \cdot \bcancel{N} \cdot \overline{W_{kin}} = \bcancel{N} \cdot k_B \cdot T \\[5px]
\label{kin}
& \boxed{\overline{W_{kin}} = \frac{3}{2} k_B \cdot T} \\[5px]
\end{align}

Die mittlere kinetische Energie der Teilchen ist nur von der Temperatur abhängig!

Auch an dieser Stelle bezieht sich die kinetische Energie wieder nur auf die translatorische Bewegung und nicht auf die Rotationsbewegung. Rotationsenergien haben keinen Einfluss auf die Temperatur!

Innere Energie eines idealen Gases

Da gemäß Gleichung (\ref{kin}) jedes Teilchen im Mittel die Energie 3/2⋅k_BT trägt, kann die Gesamtenergie der Teilchen und damit die Energie des Gases durch Multiplikation mit der Teilchenanzahl N erhalten werden. Diese im Inneren des Gases vorhandene Gesamtenergie wird auch als innere Energie U bezeichnet:

\begin{align}
\label{u}
& \boxed{U = \frac{3}{2} N k_B T} \\[5px]
\end{align}

Wird an dieser Stelle der Ausdruck N⋅k_BT gemäß Gleichung (\ref{1}) durch p⋅V ersetzt, dann kann der Druck auch wie folgt anhand der Energiedichte u_v des Gases bestimmt werden (um Missverständnisse mit der spezifischen inneren Energie u als massebezogene Größe zu vermeiden, ist bei der volumetrischen Energiedichte im Index ein „v“ hinzugefügt):

\begin{align}
& U = \frac{3}{2} N k_B T = \frac{3}{2} pV\\[5px]
& p = \frac{2}{3} \cdot \underbrace{\frac{U}{V}}_{\text{Energiedichte } u_v} \\[5px]
& \boxed{p = \frac{2}{3} u_v} ~~~~~\text{mit } u_v=\frac{U}{V}
\end{align}

Der Druck in einem idealen Gas ist nur abhängig von der Energiedichte, d.h. der pro Volumeneinheit vorhandenen inneren Energie im Gas!