Isentroper („adiabater“) Prozess in einem geschlossenen System

Als isentroper Prozess bezeichnet man eine reversible Zustandsänderung in einem adiabaten System.

Definition

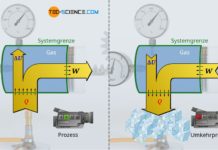
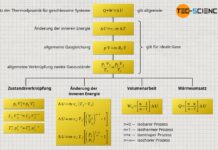
Während bei einem isochoren Prozess keine Volumenänderungsarbeit umgesetzt wird (W_V=0) und sich beim isothermen Prozess keine Änderung der inneren Energie ergibt (ΔU=0), findet bei einem sogenannten isentropen Prozess per Definition kein Wärmeumsatz über die Systemgrenze hinweg statt (Q=0). Eine isentrope Zustandsänderung muss unter der Bedingung, dass keine Wärme übertragen wird, folglich in einem adiabaten System stattfinden. Aus diesem Grund wird die isentrope Zustandsänderung auch als häufig als adiabatischer Prozess bzw. adiabater Prozess bezeichnet.

Realisierung einer näherungsweisen isentropen Zustandsänderung

Grundsätzlich ist kein System perfekt wärmeisoliert, sodass eine isentrope Zustandsänderung nur näherungsweise erfolgen kann. Aber auch wenn Systeme nicht besonders gut wärmegedämmt sind, kann man thermodynamische Prozesse unter bestimmten Voraussetzungen dennoch als näherungsweise isentrop ansehen. Dies ist zum Beispiel dann der Fall, wenn Zustandsänderungen so schnell ablaufen, dass dem System praktisch keine Zeit bleibt, um mit der Umgebung in nennenswertem Maße Wärme auszutauschen. Aus diesem Grund werden beispielsweise die innerhalb weniger Millisekunden ablaufenden Kompressions- und Expansionsvorgänge in Verbrennungsmotoren häufig als isentrop betrachtet.

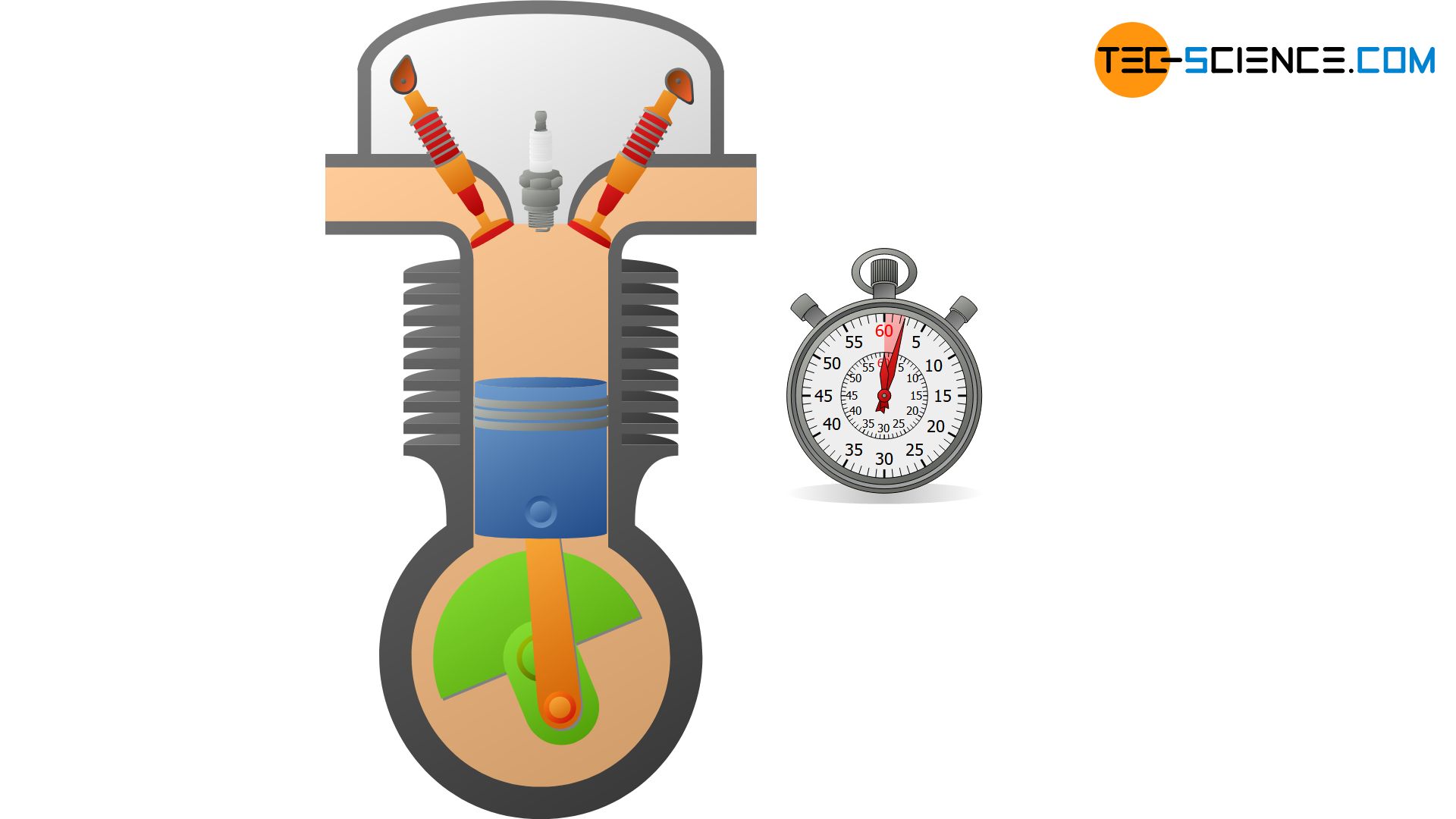
Ein geschlossenes adiabates System als Voraussetzung für den isentropen Prozess lässt sich näherungsweise mit einem gasgefüllten Zylinder realisieren, der mit einem beweglichen Kolben verschlossen. Wird das Gas nun sehr schnell komprimiert, so kann eine Wärmeübertragung auf die Umgebung vernachlässigt werden und man erhält für die Zeitdauer der Zustandsänderung ein näherungsweises adiabates System. Im Idealfall sind die Wände des Zylinders noch aus einem wärmedämmenden bzw. schlecht wärmeleitendem Material.

In der Praxis stellt das schlagartige Zusammenpressen der Luft in einer Luftpumpe näherungsweise ein isentroper Prozess dar, wenn dabei das Auslassventil verschlossen wird. Nach dem Verdichten, wird man jedoch rasch einen Druckabfall beobachten, da anschließend Wärme von der eingeschlossenen Luft auf die Innenwände der Luftpumpe übertragen wird. Die Temperatur und damit der Druck sinken wieder. Die Luftpumpe stellt dann kein adiabates System mehr dar.

Darstellung im Volumen-Druck-Diagramm

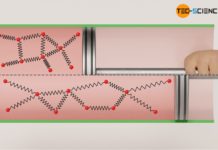
Wird ein Gas in einem adiabaten System schlagartig komprimiert, so findet aufgrund der Volumenverkleinerung zunächst eine Druckerhöhung statt. Damit verbunden ist allerdings auch eine Erhöhung der Temperatur. Dies lässt sich anschaulich damit erklären, dass die Gasteilchen durch die schlagartige Bewegung des Kolbens einen zusätzlichen Impuls beim Aufprall auf die Kolbenfläche erhalten und damit ihre Geschwindigkeit erhöhen (siehe hierzu auch den Artikel Warum erhöhen sich Druck und Temperatur bei der Kompression eines Gases?). Bei Dieselmotoren ist der Temperaturanstieg während der als isentrop betrachteten Kompression gezielt gewünscht, da hierdurch die Zündtemperatur des Dieseltreibstoffs überschritten wird und der Kraftstoff sich von selbst entzündet (Selbstzündung).

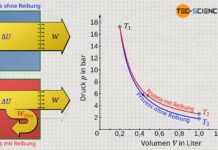
Während bei einer isothermen Kompression eine Temperaturerhöhung durch eine entsprechende Wärmeabfuhr kompensiert wird, findet bei einer isentropen Kompression keine Wärmeabfuhr statt. Deshalb ist die Druckerhöhung ist bei einer isentropen Kompression größer als bei einer isothermen Kompression. Denn während bei einer isothermen Verdichtung die Druckerhöhung alleine aus der Volumenverkleinerung resultiert (die Temperatur bleibt ja konstant), findet bei einer isentropen Kompression zusätzlich eine Temperaturerhöhung statt. Diese Temperatursteigerung erhöht den Druck zusätzlich. Aus diesem Grund verläuft die isentrope Zustandsänderung im Volumen-Druck-Diagramm auf einem höheren Druckniveau und damit stets oberhalb der Zustandsänderung des isothermen Vergleichsprozesses.

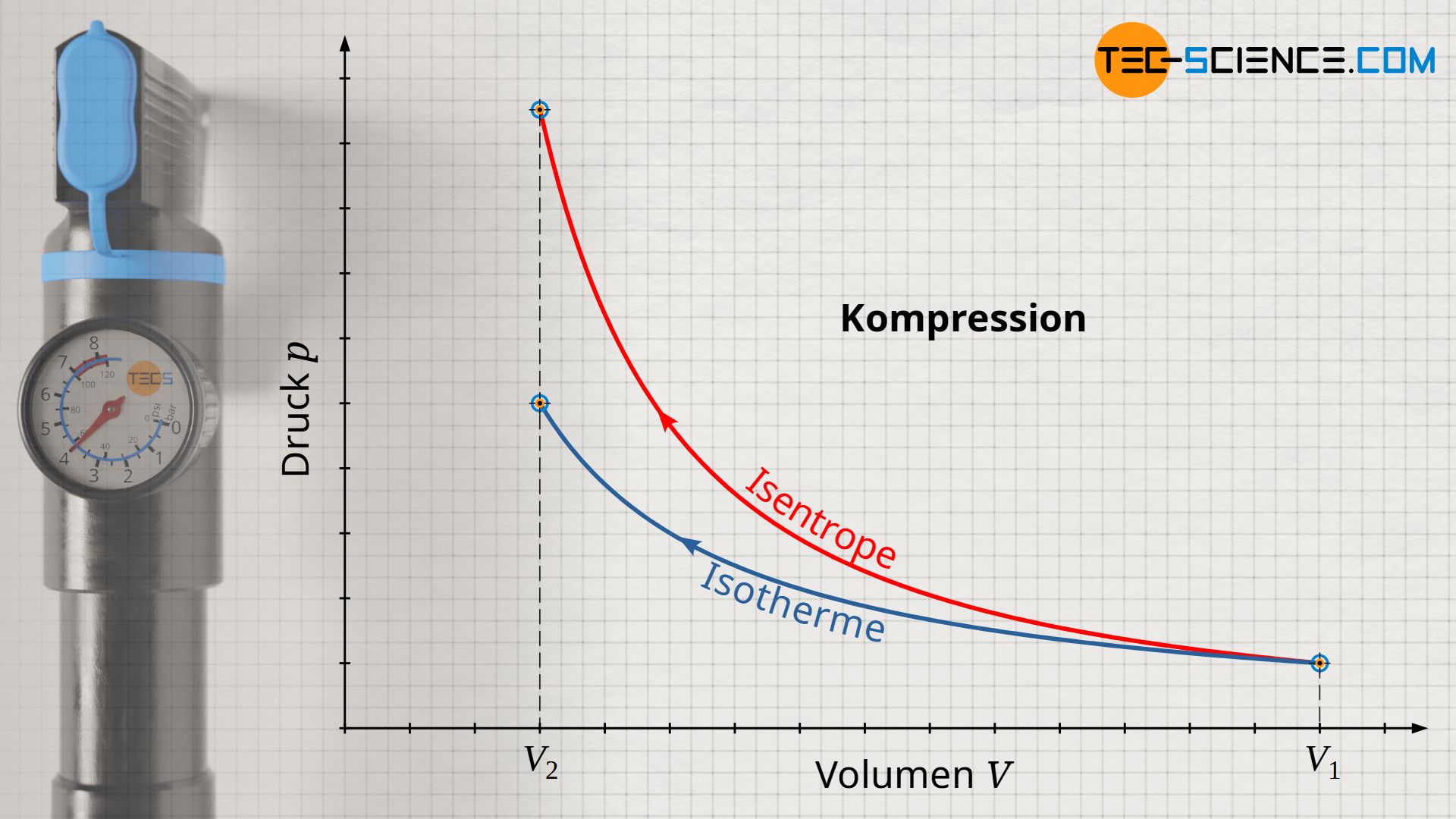
Umgekehrt sinkt der Druck bei einer isentropen Expansion auf einen niedrigeren Wert ab im Vergleich zur isothermen Expansion. Auch dies kann anschaulich erklärt werden. Denn um die Temperatur bei einer isothermen Expansion konstant zu halten, wird dem Gas Wärme zugeführt. Die Teilchen behalten aufgrund der konstanten Temperatur offensichtlich ihre Bewegungsenergie bei (konstante innere Energie). Bei der isentropen Expansion wird dem Gas hingegen keine Wärmeenergie zugeführt, um die Temperatur konstant zu halten. Die Temperatur sinkt entsprechend ab. Die Druckerniedrigung resultiert bei der isentropen Expansion also nicht nur aus der Volumenvergrößerung, sondern zusätzlich noch aus der Temperaturerniedrigung. Die isentrope Expansion verläuft im Volumen-Druck-Diagramm demzufolge auf einem geringeren Druckniveau im Vergleich zu einer isothermen Expansion.

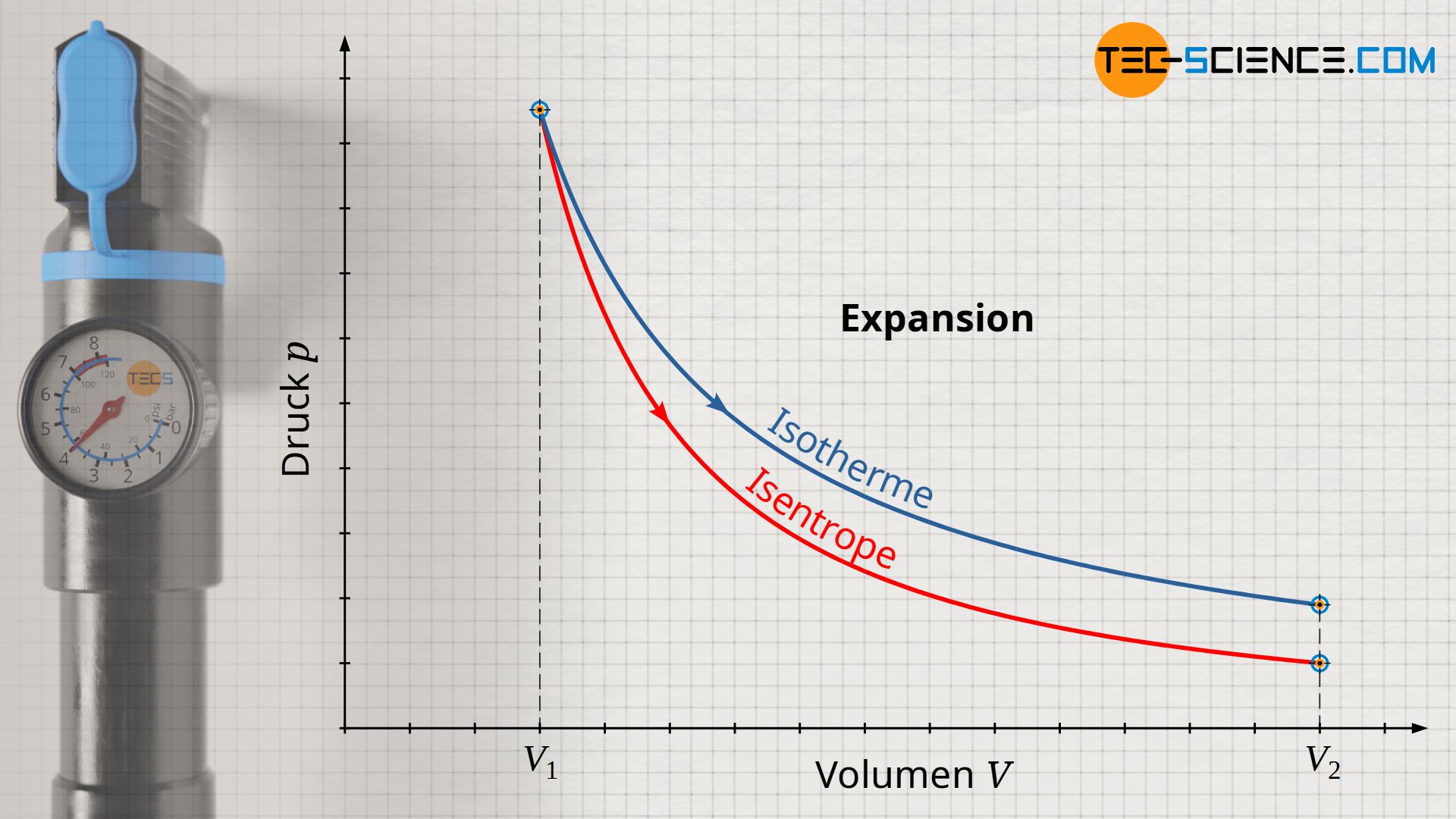
Die isentrope Zustandsänderung verläuft im Volumen-Druck-Diagramm steiler im Vergleich zu einem isothermen Prozess! 

Zusammenhang zwischen Volumen, Druck und Temperatur

Solange das Gas bei einer isentropen Zustandsänderung als ideales Gas betrachtet wird, gilt unabhängig des genauen thermodynamischen Prozesses nach wie vor die ideale Gasgleichung, mit Hilfe deren zwei Zustände wie folgt miteinander verknüpft sind:

\begin{align}
&\boxed{p \cdot V = R_\text{s} \cdot m \cdot T} ~~~\text{ideale Gasgleichung} \\[5px]
&{p \cdot V \over T}=R_\text{s} \cdot m = \text{konstant} \\[5px]
\label{kurz}
\Rightarrow~ &\boxed{{p_1~V_1 \over T_1}={p_2~V_2 \over T_2} }\\[5px]
\end{align}

Während sich an dieser Stelle bei einem isobaren Prozess der konstante Druck, bei einem isochoren Prozess das konstante Volumen, und bei einem isothermen Prozess die konstante Temperatur aus Gleichung (\ref{kurz}) herauskürzt, lassen sich bei einem isentropen Prozess nun keine konstanten Zustandsgrößen finden, die sich gegenseitig herauskürzen.

Es können jedoch eindeutige Zusammenhänge zwischen jeweils zwei Zustandsgrößen hergeleitet werden, wenn neben der idealen Gasgleichung zusätzlich noch die spezielle Bedingung für den isentropen Prozess mit Q=0 im ersten Hauptsatz der Thermodynamik berücksichtigt wird. Nach komplexerer mathematischer Herleitung (siehe Artikel Herleitung der Formeln für den isentropen „adiabaten“ Prozess), ergeben sich folgende Zusammenhänge bei einem isentropen Prozess:

\begin{alignat}{3}
\label{2}
&p \cdot V^\kappa = \text{konstant}& &\Rightarrow&~ &\boxed{ p_1~V_1^\kappa = p_2~V_2^\kappa} \\[5px]
\label{3}
&T \cdot V^{\kappa-1} = \text{konstant}& &\Rightarrow&~ &\boxed{ T_1~V_1^{\kappa-1} = T_2~V_2^{\kappa-1}} \\[5px]
\label{4}
&T^\kappa \cdot p^{1-\kappa} = \text{konstant}& &\Rightarrow&~ &\boxed{ T_1^\kappa~p_1^{1-\kappa} = T_2^\kappa~p_2^{1-\kappa}} \\[5px]
\label{1}
&&&&&\text{ mit } \boxed{\kappa = {c_\text{p} \over c_\text{v}}}>1 \\[5px]
\end{alignat}

Da bei der Herleitung dieser Gleichungen der Quotient aus den spezifischen Wärmekapazitäten c_p und c_v sehr häufig auftritt, wird dieser praktischerweise zum sogenannten Isentropenexponent κ (Adiabatenexponent) zusammengefasst. Dieser Isentropenexponent ist einheitenlos und grundsätzlich größer 1, da die spezifische Wärmekapazität c_p stets größer c_v ist (siehe hierzu auch den Artikel Spezifische Wärmekapazität von Gasen).

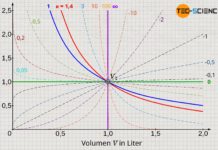
Betrachtet man den Zusammenhang zwischen Druck und Volumen gemäß Gleichung (\ref{2}), so wird nun auch auf mathematischem Wege deutlich, dass die Zustandsänderung im Volumen-Druck-Diagramm für einen isentropen Prozess steiler verläuft als die des isothermen Prozesses:

\begin{align}
&p \cdot V^\kappa = \text{konstant} \\[5px]
&\boxed{p \sim {1 \over V^\kappa}} ~~~\text{isentroper Prozess}\\[5px]
&\boxed{p \sim {1 \over V}} ~~~\text{isothermer Prozess}\\[5px]
\end{align}

Beim isothermen Prozess nimmt der Druck mit größer werdendem Volumen nach der Gesetzmäßigkeit p~1/V ab. Bei der isentropen Zustandsänderung hingegen verringert sich der Druck nach der Gesetzmäßigkeit p~1/V^κ. Da der Isentropenexponent κ allerdings stets größer 1 ist, fällt der Druck bei einer isentropen Volumenvergrößerung offensichtlich schneller ab als beim isothermen Prozess. Folglich verläuft die Isentrope im Volumen-Druck-Diagramm steiler als die Isotherme.

Berechnung der Änderung der inneren Energie

Für ideale Gase ergibt sich die Änderung der inneren Energie ΔU unabhängig des thermodynamischen Prozesses lediglich anhand der Temperaturänderung ΔT=T₂-T₁:

\begin{align}
\label{a}
&\boxed{ \Delta U = c_\text{v}~m~\left(T_2-T_1 \right)} \\[5px]
\end{align}

Wird diese Gleichung nach dem Temperaturverhältnis T₂/T₁ umgestellt, so kann die Änderung der inneren Energie bei gegebener Anfangstemperatur T₁ durch Verknüpfung mit Gleichung (\ref{3}) bzw. Gleichung (\ref{4}) auch über das Volumenverhältnis bzw. das Druckverhältnis ermittelt werden:

\begin{align}
& \Delta U = c_\text{v}~m~\left(T_2-T_1 \right) \\[5px]
& \Delta U = c_\text{v}~m~T_1~\left[{T_2 \over T_1}-1 \right] \\[5px]
& \boxed{\Delta U = c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{\kappa-1}}-1 \right]} \\[5px]
\label{c}
& \boxed{\Delta U = c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-\kappa} \over \kappa}}-1 \right]} \\[5px]
\end{align}

Berechnung der Volumenänderungsarbeit

Wie bei jedem (reversiblen) thermodynamischen Prozess ergibt sich die Volumenänderungsarbeit des Gases als Fläche unterhalb der Zustandskurve im Volumen-Druck-Diagramm. Diese Fläche lässt sich grundsätzlich durch Integration der Druckfunktion p(V) ermitteln. Bei genauerer Betrachtung des ersten Hauptsatzes der Thermodynamik zeigt sich allerdings, dass unter der Bedingung Q=0 die Volumenänderungsarbeit gerade der Änderung der inneren Energie entspricht:

\begin{align}
&\boxed{W_\text{V} + Q = \Delta U} ~~~\text{Erster Hauptsatz}\\[5px]
&\boxed{W_\text{V} = \Delta U} \\[5px]
\end{align}

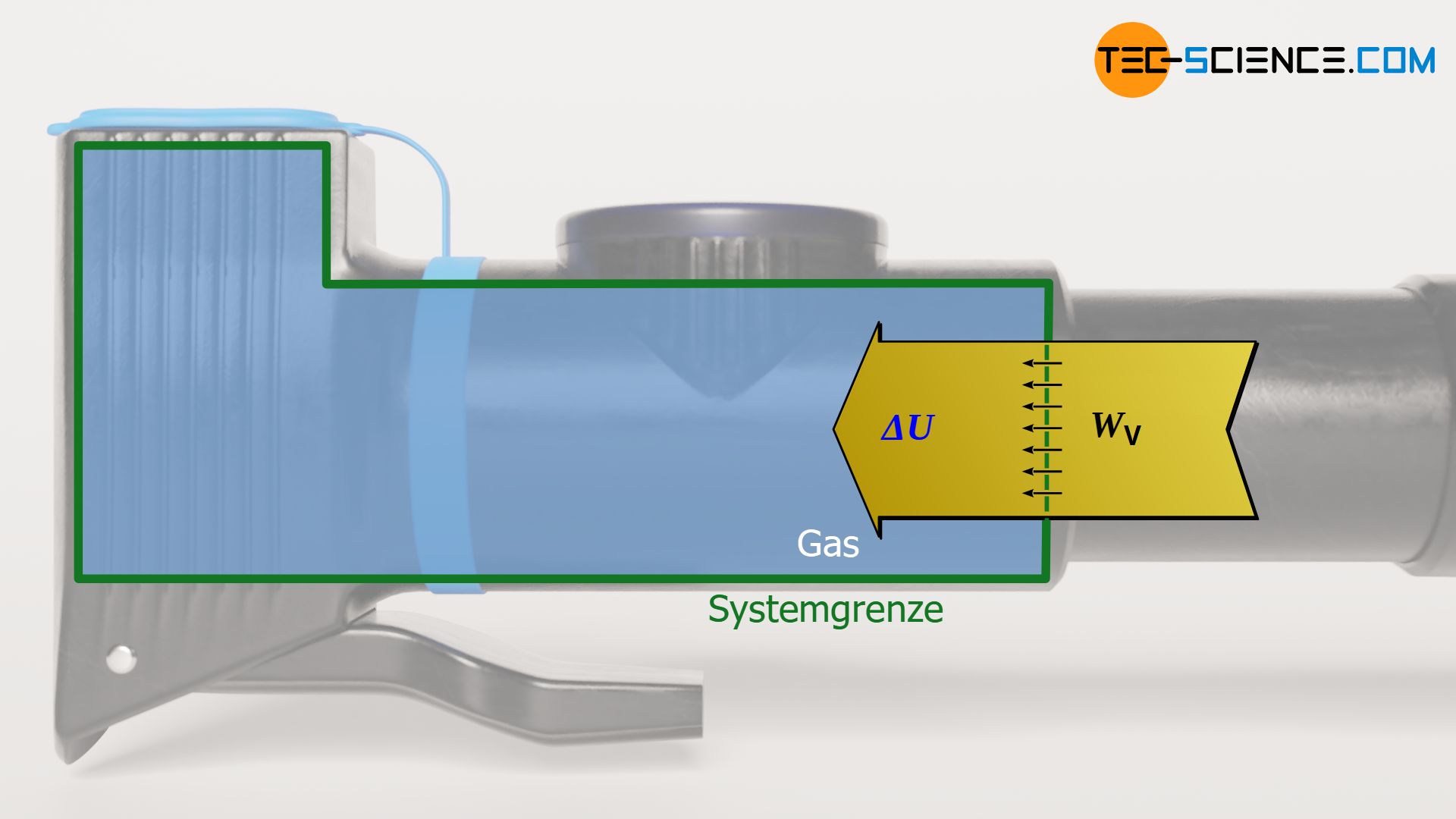
Dass die Änderung der inneren Energie gerade der Volumenänderungsarbeit entspricht, wird auch anschaulich sehr schnell klar. Aufgrund des fehlenden Wärmeumsatzes muss bei einer Kompression die am Gas verrichtete Volumenänderungsarbeit vollständig der inneren Energie zugutekommen. Umgekehrt vollzieht sich eine vom Gas erbrachte Volumenänderungsarbeit vollständig auf Kosten der inneren Energie, da sie offensichtlich nicht aus einem Wärmeumsatz entstammen kann. Zur Berechnung der Volumenänderungsarbeit W_V während eines isentropen Prozesses können also die Gleichungen (\ref{a}) bis (\ref{c}) benutzt werden:

\begin{align}
& W_\text{V} = c_\text{v}~m~\left(T_2-T_1 \right) \\[5px]
&W_\text{V} = c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{\kappa-1}}-1 \right] \\[5px]
&W_\text{V} = c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-\kappa} \over \kappa}}-1 \right] \\[5px]
\end{align}

Wichtige Anmerkung

Achtung: Nicht alle Prozesse, die in einem adiabaten System ablaufen, müssen zwangsweise den in diesem Artikel erläuterten Gleichungen folgen! Deshalb ist die Bezeichnung adiabatischer Prozess an mancher Stelle auch etwas irreführend. Die strenge Definition des isentropen Prozesses lautet wie folgt:

Ein isentroper Prozess ist eine reversible Zustandsänderung eines adiabaten Systems!

An dieser Stelle ist der Begriff „reversibel“ entscheidend! Mehr Informationen, speziell zu dieser Thematik, finden sich auch im Artikel Freie Ausdehnung eines idealen Gases im Vakuum.