Als Auftrieb bezeichnet man die entgegen der Schwerkraft gerichtete Kraft, die ein Körper beim Eintauchen in ein Fluid (Flüssigkeit oder Gas) erfährt.
Einleitung
Jeder hat wahrscheinlich schon einmal versucht eine andere Person hochzuheben und dabei festgestellt, dass hierfür ein erheblicher Kraftaufwand erforderlich ist. Versucht man hingegen diese Person im Wasser hochzuheben, so ist dies deutlich einfacher. Ursache hierfür liegt in der sogenannten Auftriebskraft, die ein Körper erfährt sobald dieser in einer Flüssigkeit eintaucht. Diese Auftriebskraft ist auch dafür verantwortlich, dass tonnenschwere Schiffe aus Stahl im Wasser nicht untergehen. Auf die Ursache der Auftriebskraft wird im folgenden Artikel näher eingegangen werden.

Demonstration der Auftriebskraft
Mit folgendem Experiment soll die Wirkung der Auftriebskraft demonstriert werden. An einem Quader aus Metall wird ein Federkraftmesser befestigt. Ohne den Boden zu berühren wird das Metallstück allmählich in ein Glas mit Wasser eingetaucht und der Federkraftmesser dabei beobachtet.
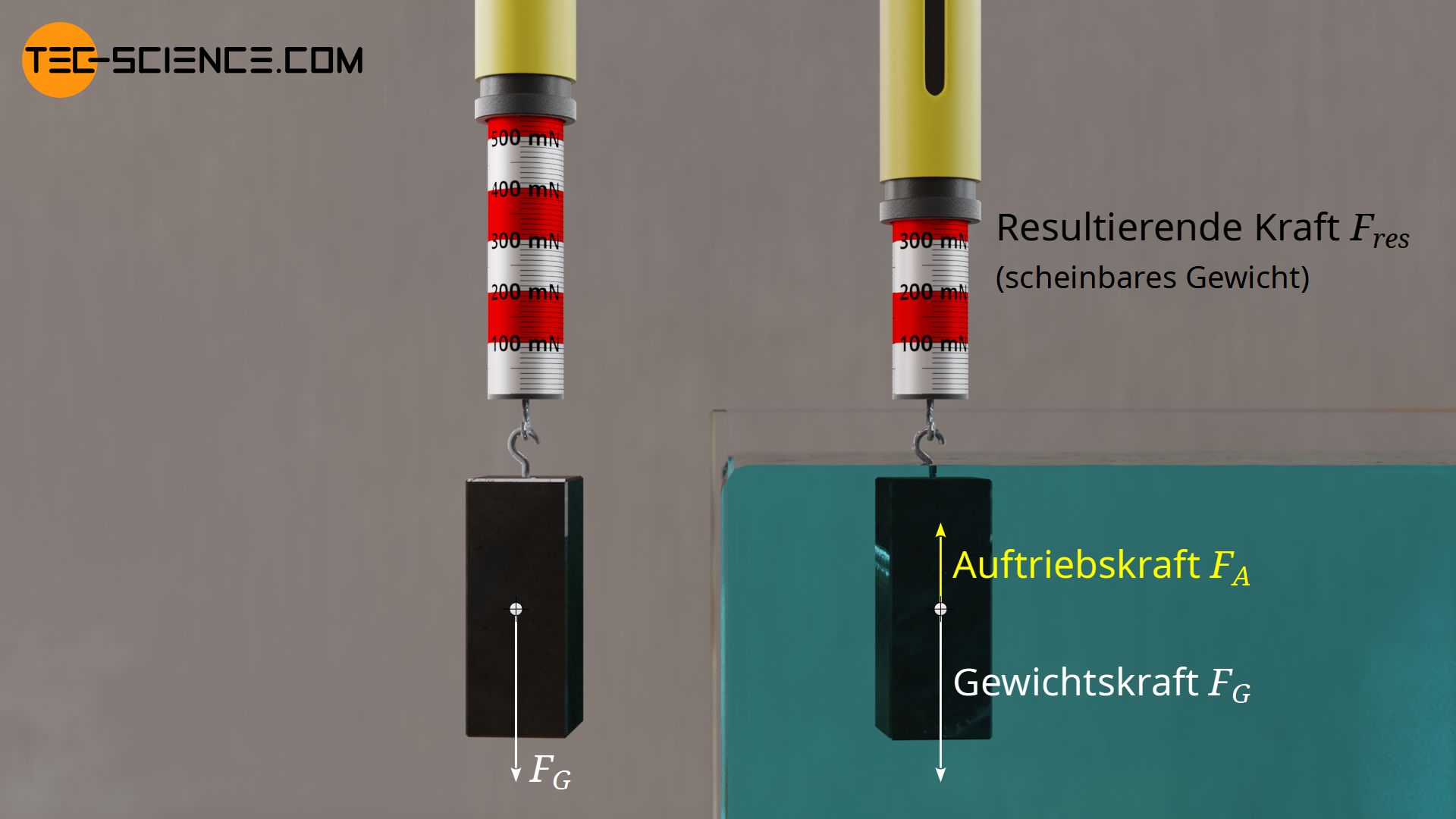
Hat das Metallstück das Wasser erreicht, so nimmt mit steigender Eintauchtiefe der Ausschlag des Kraftmessers stetig ab. Erst wenn der Quader vollständig mit Wasser umgeben ist, zeigt der Federkraftmesser wieder einen konstanten Wert an. Der abnehmende Anzeigewert hat nicht etwa mit einer abnehmenden Gewichtskraft zu tun, denn schließlich ändert sich die Masse des Metallklotzes nicht. Vielmehr nimmt mit steigender Eintauchtiefe die entgegen der Schwerkraft wirkende Auftriebskraft zu. Die Auftriebskraft entspricht dabei dem Betrag um den der Körper im Wasser scheinbar leichter geworden ist.
Die auf einen Körper wirkende Auftriebskraft ist umso größer, je mehr der Körper in die Flüssigkeit eintaucht! Die Auftriebskraft ist dabei stets der Schwerkraft entgegengesetzt gerichtet!
Die Auftriebskraft : Das archimedisches Prinzip
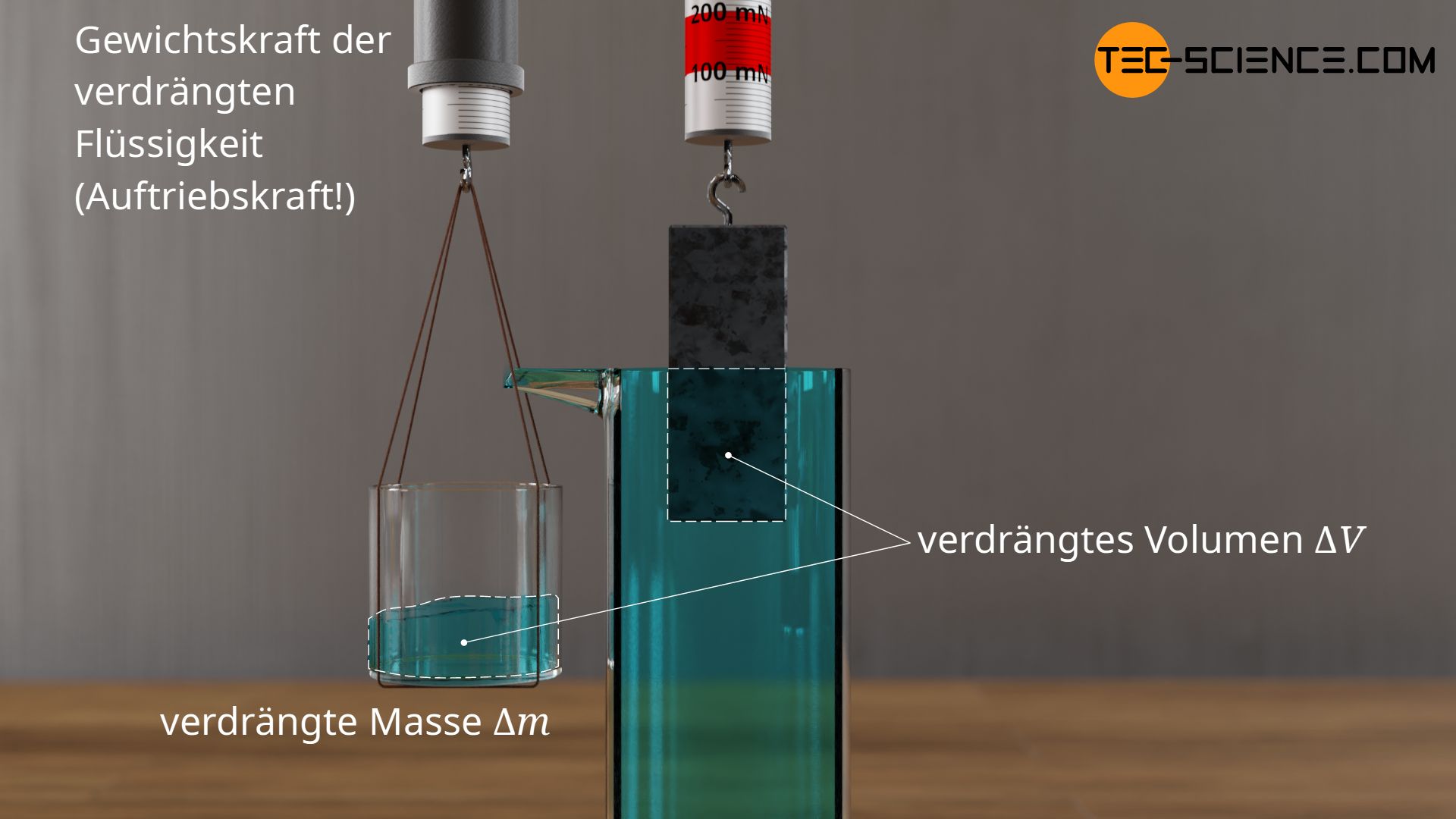
Der Wissenschaftler Archimedes beschäftigte sich mit dem Thema Auftrieb bereits 250 Jahre v. Chr. Durch Versuche konnte er dabei zeigen, dass die Auftriebskraft um die ein eingetauchter Körper scheinbar leichter wird, der Gewichtskraft der verdrängten Flüssigkeit entspricht. Als verdrängte Flüssigkeit bezeichnet man die Menge an Flüssigkeit, die dem eingetauchten Körper weichen muss, wenn dieser eintaucht. Anschaulich entspricht dies jener Flüssigkeitsmenge, die bei einem randvoll gefüllten Glas überlauft, wenn man darin den Körper bis zu einer bestimmten Tiefe eintaucht. Die Gewichtskraft dieser übergelaufenen Flüssigkeit entspricht dann der Auftriebskraft. Diese Aussage wird auch als Archimedisches Prinzip bezeichnet.

Das Archimedische Prinzip besagt, dass die Auftriebskraft eines Körpers der Gewichtskraft der verdrängten Flüssigkeit entspricht!
Wenn ein Körper vollständig in die Flüssigkeit eintaucht, dann entspricht das Volumen der verdrängten Flüssigkeit offensichtlich dem Volumen des eingetauchten Körpers. Besitzt der 54 g schwere Metallquader aus Aluminium bspw. eine quadratische Grundfläche von 4 cm² und einer Höhe von 5 cm, dann ergibt sich hieraus ein Quadervolumen von 20 cm³ (20 ml). Dementsprechend verdrängt der Körper beim vollständigen eintauchen in Wasser eine Flüssigkeitsmenge von 20 ml. Dies entspricht bei einer Wasserdichte von 1 g pro cm³ einer verdrängten Wassermasse von 20 g. Der 54 g schwere Metallquader fühlt sich unter Wasser folglich um 20 g leichter an. Ein Federkraftmesser würde anstelle von 540 mN folglich nur 340 mN anzeigen.
Beachte, dass sich durch das Eintauchen des Körpers nicht dessen Gewichtskraft ändert, sondern nun eine entgegen der Gewichtskraft wirkende Auftriebskraft wirksam ist, die nun eine insgesamt verringerte resultierende Gesamtkraft zur Folge hat. Es ist deshalb auch ratsam nicht mit den Massen zu argumentieren (auch wenn dies anschaulicher ist), sondern mit den Kräften! Wird die Gewichtskraft des Körpers mit \(F_G\) bezeichnet und die entgegenwirkende Auftriebskraft mit \(F_A\), dann gilt für die resultierende Kraft \(F_{res}\) die der Körper erfährt:
\begin{align}
\label{res}
&\boxed{F_{res} = F_G – F_A} \\[5px]
\end{align}
Sollte der Metallquader nicht vollständig in die Flüssigkeit eintauchen, sondern nur teilweise, dann verdrängt dieser auch offensichtlich nicht so viel Wasser. Letztlich wird ein Körper immer nur so viel Flüssigkeit verdrängen wie Körpervolumen auch tatsächlich eintaucht. Tauch nur die Hälfte des Körpervolumens ein, dann verdrängt der Körper auch nur die Hälfte des Wassers. Dementsprechend ist die Auftriebskraft auch nur halb so groß. Bezeichnet \(\Delta V\) das eingetauchte Körpervolumen bzw. das verdrängte Flüssigkeitsvolumen und \(\rho_F\) die Dichte der Flüssigkeit, dann gilt für die Masse der verdrängten Flüssigkeit \(\Delta m\):
\begin{align}
&\Delta m = \Delta V \cdot \rho_F \\[5px]
\end{align}
Für die Auftriebskraft \(F_A\) als Gewichtskraft der verdrängten Flüssigkeit gilt dann schließlich:
\begin{align}
&F_A = \Delta m \cdot g \\[5px]
\label{arch}
&\boxed{F_A = \Delta V \cdot \rho_F \cdot g} \\[5px]
\end{align}
Herleitung der Auftriebskraft
Das Zustandekommen der Auftriebskraft ist den unterschiedlichen hydrostatischen Drücken an der Ober- und Unterseite eines eingetauchten Körpers geschuldet. Der Einfachheit halber wird an dieser Stelle wieder ein quaderförmiger Gegenstand betrachtet, der vollständig in die umgebende Flüssigkeit eintaucht.
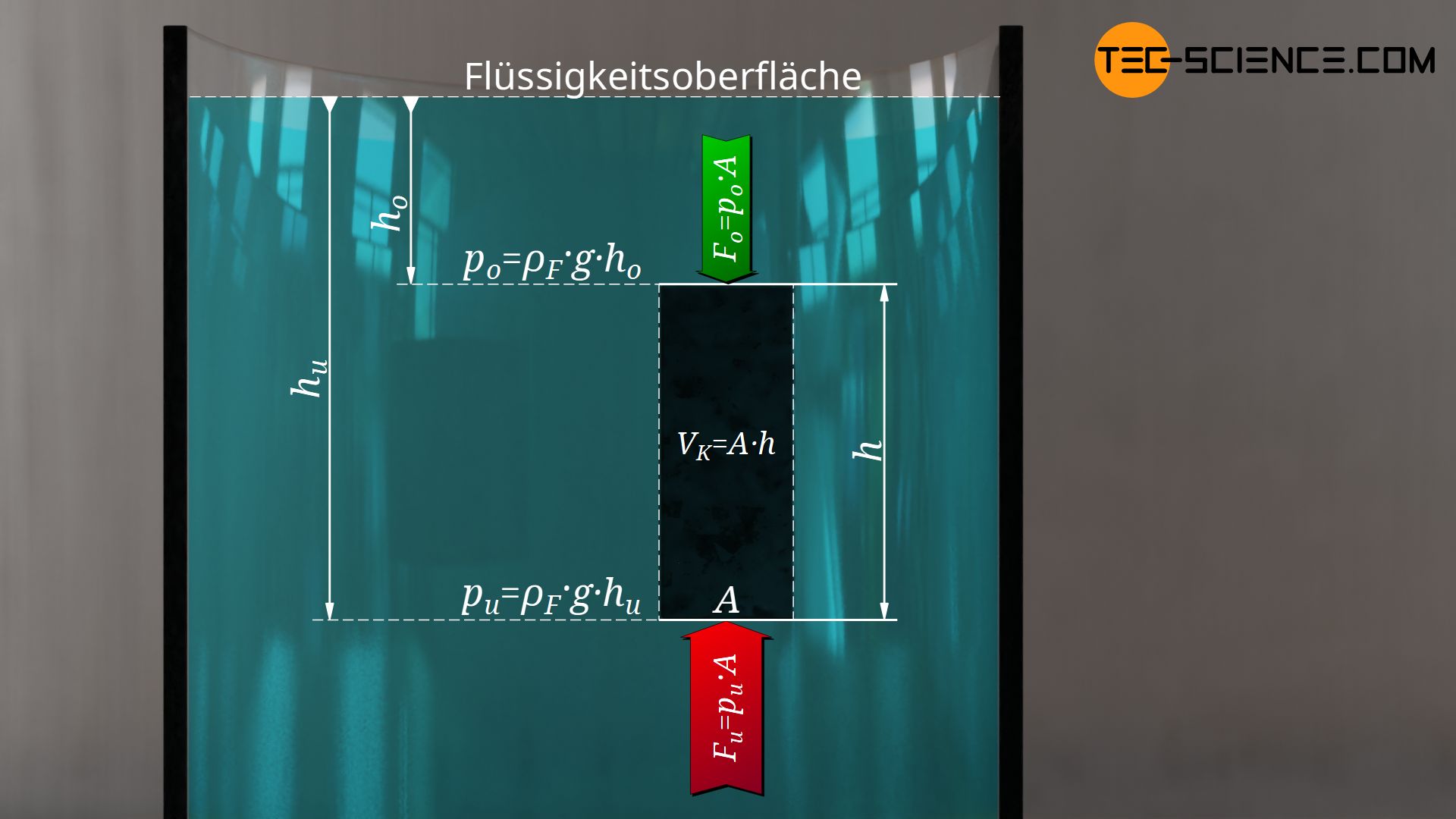
Im Artikel Druck in Flüssigkeiten wurde bereits ausführlich das Zustandekommen der Flüssigkeitsdrücke erläutert. Sie ergeben sich lediglich anhand der Tiefe unterhalb der Flüssigkeitsoberfläche. Je tiefer ein Punkt unterhalb der Flüssigkeitsoberfläche liegt, desto größer ist der Flüssigkeitsdruck und die damit verbundene Kraft auf eine Fläche. Auf diese Weise ist die nach oben gerichtete Kraft an der Unterseite des Körpers folglich großer als die nach unten gerichtete Kraft auf der Oberseite. Somit wirkt effektiv eine Kraft nach oben, die Auftriebskraft!
Der Flüssigkeitsdruck an der Unterseite ermittelt sich anhand der Tiefe \(h_u\) wie folgt:
\begin{align}
&p_u = \rho_F \cdot g \cdot h_u \\[5px]
\end{align}
Darin bezeichnet \(\rho_F\) die Dichte der betrachteten Flüssigkeit. Analog gilt für den hydrostatischen Druck in der Tiefe \(h_o\) an der Oberseite des Quaders:
\begin{align}
&p_o = \rho_F \cdot g \cdot h_o \\[5px]
\end{align}
Die entsprechenden Kräfte an der Unter- bzw. Oberseite des Quaders ermitteln sich gemäß der Definition des Drucks durch Multiplikation von Druck und Fläche (\(F=p \cdot A\)). Als Fläche ist im vorliegenden Fall die Grundfläche \(A\) des Quaders gemeint:
\begin{align}
&\underline{F_u = \rho_F \cdot g \cdot h_u \cdot A} ~~~~~\text{bzw.}~~~~~ \underline{F_o = \rho_F \cdot g \cdot h_u \cdot A} \\[5px]
\end{align}
Die resultierende Auftriebskraft \(F_A\), mit der der Körper aufgrund der unterschiedlichen Kräfte nach oben gedrückt wird, ergibt sich aus deren Differenz:
\begin{align}
&F_A = F_u – F_o \\[5px]
&F_A = \rho_F \cdot g \cdot h_u \cdot A – \rho_F \cdot g \cdot h_o \cdot A \\[5px]
\label{d}
&F_A = \rho_F \cdot g \cdot A \cdot \left(h_u-h_o\right) \\[5px]
\end{align}
Die Differenz in den Tiefen entspricht gerade der Höhe \(h\) des Quaders. Ferner kann ausgenutzt werden, dass das Produkt von Höhe und Grundfläche dem Volumen \(V_K\) des eingetauchten Körpers entspricht:
\begin{align}
&F_A = \rho_F \cdot g \cdot A \cdot \underbrace{\left(h_u-h_o\right)}_{=h} \\[5px]
&F_A = \rho_F \cdot g \cdot \underbrace{A \cdot h}_{=V_K} \\[5px]
\label{ein}
&\boxed{F_A = V_K \cdot \rho_F \cdot g}~~~~~\text{Auftriebskraft bei vollständigem Eintauchen} \\[5px]
\end{align}
Beachte, dass es für die Auftriebskraft offensichtlich keine Rolle spielt in welcher Tiefe sich der Gegenstand genau befindet. Aus Gleichung (\ref{d}) wird bereits deutlich, dass lediglich die Differenz in der Tiefe zwischen Ober- und Unterseite relevant ist, d.h. die Höhe des Gegenstandes*. In Kombination mit der Fläche ergibt sich hieraus lediglich die Abhängigkeit von dessen Volumen. Diese Formel wurde der Einfachheit halber zwar anhand eines Quaders hergeleitet, sie gilt aber prinzipiell für jeden beliebig geformten Gegenstand, solange dieser mit seinem Volumen \(V_K\) vollständig in die Flüssigkeit eintaucht (eine allgemeinere Herleitung der Auftriebskraft, die auch beliebig geformte Körper berücksichtigt, zeigt der nächste Abschnitt „Herleitung des archimedischen Prinzips„).
*) Aus diesem Grund spielt auch der auf der Flüssigkeitsoberfläche lastende Umgebungsdruck keine Rolle, der normalerweise zusätzlich zum hydrostatischen Druck den Gesamtdruck ausmacht. Denn dieser Umgebungsdruck wirkt zusätzlich gleichermaßen sowohl auf die Oberseite als auch die Unterseite des Körpers und kompensiert sich somit gegenseitig.
Befindet sich ein Gegenstand nicht wie bei der bisherigen Herleitung betrachtet vollständig in der Flüssigkeit, sondern taucht nur teilweise ein, dann bezieht sich das Volumen \(V_K\) auch nur auf den tatsächlich eingetauchten Teil des Körpervolumens \(\Delta V\) (= verdrängtes Flüssigkeitsvolumen). Dabei kommt die auftreibende Kraft alleine durch den hydrostatischen Druck an der Unterseite des Körpers zustande:
\begin{align}
F_A &= F_u \\[5px]
&= p_u \cdot A \\[5px]
&= \rho_F \cdot g \cdot \underbrace{h_u \cdot A}_{\Delta V} \\[5px]
\end{align}
\begin{align}
&\boxed{F_A = \Delta V \cdot \rho_F \cdot g} ~~~~~\text{gilt allgemein} \\[5px]
\end{align}
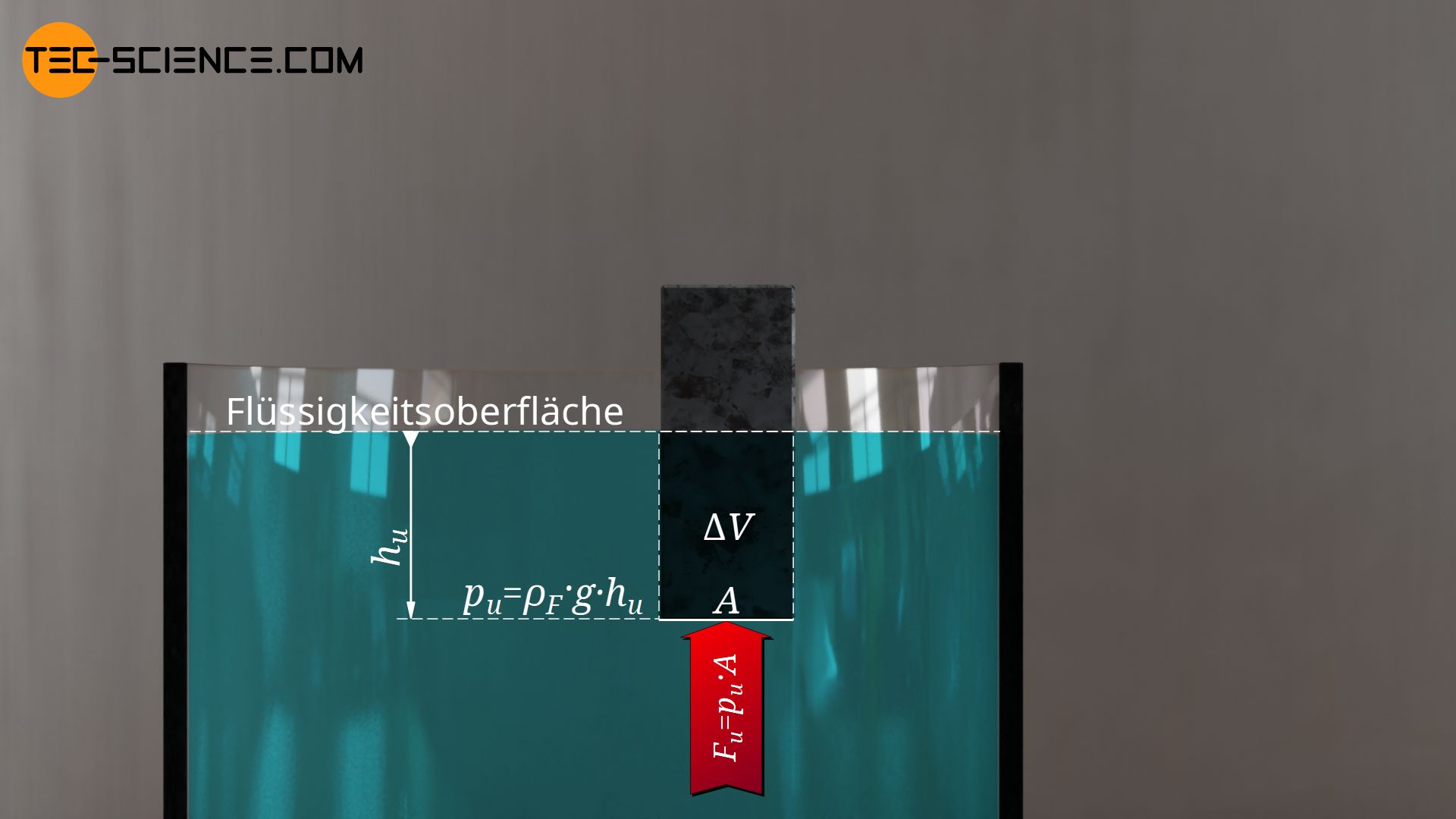
An dieser Stelle kann man nun auch das Archimedische Prinzip erkennen. So lässt sich in der oberen Formal das Produkt von verdrängtem Flüssigkeitsvolumen \(\Delta V\) und Flüssigkeitsdichte \(\rho_F\) als Masse der verdrängten Flüssigkeit interpretieren. Ferner ergibt dann das Produkt von verdrängter Flüssigkeitsmasse \(\Delta m\) und Fallbeschleunigung \(g\) die Gewichtskraft der verdrängten Flüssigkeit \(F_{G,ver}\):
\begin{align}
&F_A = \underbrace{\Delta V \cdot \rho_F}_{\Delta m} \cdot g \\[5px]
&F_A = \underbrace{\Delta m \cdot g}_{F_{G,ver}} \\[5px]
&\boxed{F_A = F_{G,ver}} \\[5px]
\end{align}
Herleitung des archimedischen Prinzips für beliebig geformte Körper
Die Herleitung der Auftriebskraft im Abschnitt zuvor erfolgte anhand eins Gegenstandes mit einer relativ simplen Geometrie, auf den die wirkenden Kräfte relativ einfach berechnet werden konnten. Dass die hergeleitete Formel aber nicht nur bei solch einfach geformten Gegenständen angewendet werden kann, sondern das Archimedische Prinzip für beliebig geformte Körper gilt, soll im Folgenden gezeigt werden.
Betrachtet wird hierzu ein mit Wasser gefülltes Gefäß. Im Artikel Druck in Flüssigkeiten wurde bereits ausführlich erläutert, dass der hydrostatische Druck in einer Flüssigkeit aufgrund der Gewichtskraft der darüber befindlichen Flüssigkeitssäule zustande kommt. Wird bspw. der Druck am Boden des linken Gefäßes betrachtet, so ergibt sich der Flüssigkeitsdruck am Boden aus der Gewichtskraft der darüber befindlichen Wassermasse (der Gegenstand ist noch nicht eingetaucht).

Taucht man nun einen beliebig geformten Gegenstand in das Wasser, dann erfährt dieser eine bestimmte Auftriebskraft. Gemäß des dritten Newtonschen Axioms („Aktion = Reaktion“) entspricht diese vom Wasser auf den Gegenstand ausgeübte Auftriebskraft bei umgekehrter Betrachtungsweise (d.h. aus Sicht des Wassers) derjenigen Kraft, die der Gegenstand zusätzlich auf das Wasser ausübt! Die Kraft auf den Gefäßboden ergibt sich somit aus Summe von Gewichtskraft des Wassers \(F_{G,Wasser}\) und Auftriebskraft \(F_A\):
\begin{align}
\label{fa}
&F_{Boden} = F_{G,Wasser} + F_A \\[5px]
\end{align}
Anmerkung: Beachte, dass wenn der eingetauchte Körper in oder auf der Flüssigkeit schwimmt, die Auftriebskraft offensichtlich der Gewichtskraft des Körpers entspricht (ansonsten würde der Gegenstand zu Boden sinken). In diesem Fall wird dann auch anschaulich klar, dass auf den Gefäßboden nicht nur die Gewichtskraft der Flüssigkeit lastet sondern zusätzlich noch die Gewichtskraft des schwimmenden Gegenstandes. Für den allgemeinen Fall eines nicht-schwimmenden Gegenstandes (wie im Falle des zuvor betrachteten Quaders, der mittels eines Federkraftmessers in das Wasser eingetaucht wurde), lastet aber nicht die gesamte Gewichtskraft des Körpers auf das Wasser, sondern nur die Gewichtskraft abzüglich der Kraft mit dem der Gegenstand gehalten wird. Diese Differenz entspricht gerade der Auftriebskraft (siehe hierzu auch Abbildung Demonstration des archimedischen Prinzips)! Deshalb ergibt sich die Kraft auf den Gefäßboden im allgemeinen Fall stets aus der Summe von Gewichtskraft der Flüssigkeitssäule und der Auftriebskraft des eingetauchten Gegenstandes.
Im Artikel Druck in Flüssigkeiten wurde bereits ausführlich erläutert, dass sich der hydrostatische Druck aus energetischen Gründen nur anhand der betrachteten Tiefe unterhalb der Wasseroberfläche ergibt. Bezüglich des Drucks am Boden verhält sich das Wasser mit dem eingetauchten Gegenstand also genauso wie ein Gefäß das lediglich mit Wasser befüllt ist und dabei denselben Wasserstand aufweist (Prinzip der kommunizierenden Röhren) – siehe hierzu die beiden rechten Gefäße in der oberen Abbildung. Man kann sich also das eingetauchte Körpervolumen auch einfach als mit Wasser gefüllt vorstellen, dies hätte offensichtlich dieselbe Wirkung auf den Gefäßboden.
Die Kraft auf den Gefäßboden ergibt sich mit dieser Sichtweise also aus der Summe der Gewichtskraft der außerhalb des gedachten Eintauchvolumens befindlichen Wassermasse \(F_{G,Wasser}\) und der Gewichtskraft der innerhalb des gedachten Eintauchvolumens befindlichen Wassermasse \(F_{G,ver}\). Letztere entspricht der Gewichtskraft der Wassermasse, den der eingetauchte Gegenstand bei der vorherigen Betrachtungsweise verdrängt. Es gilt für die zweite Betrachtungsweise also:
\begin{align}
\label{fb}
&F_{Boden} = F_{G,Wasser} + F_{G,ver} \\[5px]
\end{align}
Da beide Betrachtungsweisen offensichtlich dieselbe Kraft auf den Gefäßboden ausüben, können Gleichung (\ref{fa}) und (\ref{fb}) gleichgesetzt werden:
\begin{align}
\require{cancel}
&\bcancel{F_{G,Wasser}} + F_A = \bcancel{F_{G,Wasser}} + F_{G,ver} \\[5px]
&\boxed{F_A = F_{G,ver}} \\[5px]
\end{align}
Es zeigt sich somit, dass die Auftriebskraft direkt der Gewichtskraft der verdrängten Flüssigkeit entspricht, unabhängig davon wie der eingetauchte Gegenstand letztlich geformt ist!
Abtauchen, Auftauschen und Schweben
Ob ein vollständig eingetauchter Gegenstand bei gegebener Auftriebskraft nun untertaucht, auftaucht, oder schwebt, hängt vom Zusammenspiel zwischen Auftriebskraft und Gewichtskraft ab.
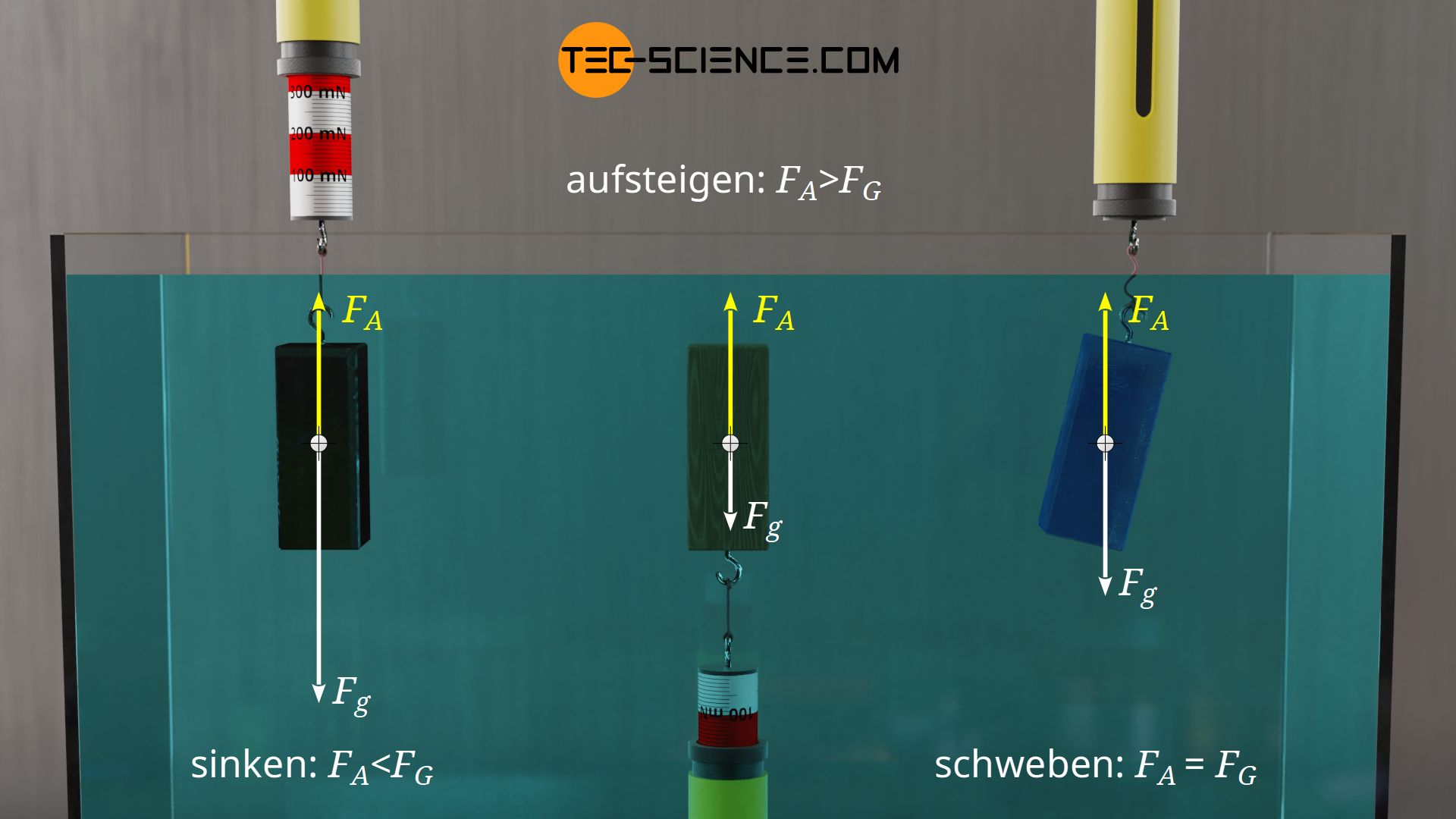
Ist die Gewichtskraft eines Körpers größer als die Auftriebskraft, dann wird dieser gemäß Gleichung (\ref{res}) mit der Differenz der Kräfte zu Boden sinken. Dies entspricht der Kraft, die der Federkraftmesser im einleitenden Beispiel anzeigt. Sollte die Auftriebskraft eines eingetauchten Gegenstandes hingegen größer sein als dessen Gewichtskraft, dann wird er mit der Differenz der Kräfte an die Oberfläche aufsteigen. Für das Anzeigen dieser resultierenden Kraft müsste der Federkraftmesser dann von unten an den Gegenstand festgemacht werden. Ist die Auftriebskraft jedoch genauso groß wie die Gewichtskraft, dann wird der Körper scheinbar schwerelos in der Flüssigkeit schweben. Ein angebrachter Federkraftmesser würde keine resultierende Kraft anzeigen, da der Gegenstand praktisch von alleine schwebt. Diese scheinbare Schwerelosigkeit in Flüssigkeiten wird beispielsweise dazu genutzt, um Astronauten gezielt auf Außeneinsätze im All vorzubereiten.
Für einen homogenen Gegenstand kann dessen Gewichtskraft über das Körpervolumen \(V_K\) und die Dichte des Körpers \(\rho_K\) ermittelt werden:
\begin{align}
&F_G = \overbrace{V_K \cdot \rho_K}^{m_K} \cdot g \\[5px]
\end{align}
Wird an dieser Stelle die Auftriebskraft nach Gleichung (\ref{ein}) verwendet, so wirkt nach Gleichung (\ref{res}) folgende resultierende Kraft auf den vollständig eingetauchten Gegenstand:
\begin{align}
&F_{res} = F_G – F_A \\[5px]
&F_{res} = V_K \cdot \rho_K \cdot g – V_K \cdot \rho_F \cdot g \\[5px]
\label{auf}
&\boxed{F_{res} = V_K \cdot g \cdot \left( \rho_K – \rho_F \right)} ~~~\text{resultierende Kraft bei vollständigem Eintauchen }\\[5px]
\end{align}
Anhand dieser Formel, können nun anschaulich die Bedingungen für ein Abtauchen, Auftauchen oder Schweben erläutert werden. Ist die Dichte des eingetauchten Körpers größer als der umgebenden Flüssigkeit, dann resultiert eine positive Kraft, die den Körper in Richtungen Boden zieht. Ist die Dichte des Körpers hingegen kleiner als die der Flüssigkeit, dann erhält man eine negative resultierende Kraft. Dies bedeutet, dass sich die Kraftrichtung umkehrt und der eingetauchte Gegenstand nun an die Oberfläche gezogen wird. Lediglich für den Fall, dass die Dichte des Körpers gerade der Dichte der Flüssigkeit entspricht, verschwindet die resultierende Kraft. Der Körper schwebt scheinbar kräftefrei in der Flüssigkeit.
Die angestellten Überlegungen der als homogen betrachteten Körper, können auch auf inhomogene Gegenstände erweitert werden, d.h. insbesondere auf Objekte, die aus unterschiedlichen Materialien und somit unterschiedlichen Dichten bestehen. Die Dichte \(\rho_K\) des betrachteten Körpers bezieht sich dann auf die mittlere Dichte, d.h. auf jene Dichte die man rechnerisch erhält, wenn man die Gesamtmasse des Körpers \(m_K\) auf dessen Gesamtvolumen \(V_K\) bezieht:
\begin{align}
&\boxed{\rho_K = \frac{m_K}{V_K}} ~~~~~\text{mittlere Dichte} \\[5px]
\end{align}
Ist die mittlere Dichte eines eingetauchten Gegenstandes geringer als die der umgebenden Flüssigkeit, so treibt der Gegenstand an die Oberfläche. Ist die mittlere Dichte größer, dann sinkt der Gegenstand zu Boden. Sind die Dichten gleich groß, so schwebt der Gegenstand in der Flüssigkeit.
Dies erklärt auch, weshalb selbst tonnenschwere Schiffe aus Stahl schwimmen können. Die mittlere Dichte eines Schiffes ist nämlich geringer als die des umgebenden Wassers. Dies wird dadurch erreicht, dass es sich bei einem Schiffsrumpf nicht um einen massiven Stahlkörper handelt, sondern lediglich nur um eine Stahlhülle. Das Innere dieses Schwimmkörpers besteht hauptsächlich aus Luft. Bezogen auf das Volumen des Schiffsrumpfes hat dieser also eine relativ geringe Masse und somit eine geringe mittlere Dichte, zumindest eine deutlich geringere (mittlere) Dichte als das umgebende Wasser. Somit sorgt der Schiffsrumpf dafür, dass bei zu starkem Eintauchen eine große resultierende auftreibende Kraft entsteht, die das gesamte Schiff über Wasser hält.

Sollte hingegen Wasser in den Schiffsrumpf eindringen, dann weicht die relativ leichte Luft dem eindringenden, schweren Wasser und die mittlere Dichte steigt an. Ist die mittlere Dichte schließlich größer als die des umgebenden Wassers (spätestens dann wenn der gesamte Schiffsrumpf vollgelaufen ist), dann wird der Schiffsrumpf bzw. das Schiff untergehen und zu Boden sinken.
Eine solche gezielte Steuerung der mittleren Dichte eines Schwimmkörpers mit Hilfe von Luft und Wasser, findet sich bspw. in U-Booten wieder. Auf diese Weise wird ein gezieltes Abtauchen und Auftauchen sowie ein Schweben im Wasser ermöglicht. Je nach Manöver wird in speziellen Ballastkammern entweder Wasser oder Luft eingelassen. Beim Abtauchen bspw. werden die luftgefüllten Kammern mit Wasser geflutet, sodass die mittlere Dichte des U-Bootes größer wird als die des umgebenden Wassers. Beim Auftauchen hingegen wird das Wasser in den Kammern mit Hilfe von Druckluft herausgepresst. Die mittlere Dichte des U-Bootes sinkt wieder und tauch schließlich auf. Beim Schweben im Wasser sind die Kammern nur teilweise mit Wasser bzw. Luft gefüllt, sodass die mittlere Dichte exakt dem Wert des umgebenden Wassers entspricht.
Die Tatsache, dass Stoffe mit geringeren Dichten als das umgebende Medium nach oben aufsteigen bzw. Stoffe mit größeren Dichten nach unten sinken, spielt auch bei Meeresströmungen eine große Rolle. Diese kommen unter anderem nämlich genau dadurch zustande, dass kaltes und damit schweres Wasser nach unten absinkt, während wärmeres und damit leichteres Wasser nach oben aufsteigt. Verursacht werden diese Dichteunterschiede aber nicht nur durch Temperatureinflüsse sondern auch durch den Salzgehalt. In stark salzhaltigen Gewässern ist die Dichte höher als in salzärmeren Regionen.
Eintauchtiefe beim Treiben an der Oberfläche (Tiefgang)
Beim Auftauchen von Gegenständen zeigt die Erfahrung, dass diese nicht vollständig mit ihrem Volumen aus der Flüssigkeit auftauchen. Ein bestimmter Teil wird sich weiterhin unter der Flüssigkeitsoberfläche befinden, während der Rest oberhalb der Wasseroberfläche treibt. Ein einfaches Alltagsbeispiel an dem dies deutlich wird, sind Schiffe, deren Schiffsrümpfe offensichtlich nur teilweise in das Wasser eintauchen. Es stellt sich dabei natürlich die Frage, wie man diese Eintauchtiefe, die bei Schiffen auch als Tiefgang bezeichnet wird, ermitteln kann.

Treibt ein Gegenstand an der Oberfläche, so taucht dieser offensichtlich weder auf noch ab. Es wirkt folglich keine resultierende Kraft auf den Körper, sodass Kräftegleichgewicht zwischen der nach unten wirkenden Gewichtskraft und der nach oben getrieben Auftriebskraft herrscht:
\begin{align}
&F_{res} = F_G – F_A \overset{!}{=}0 \\[5px]
&\underline{F_A = F_G} \\[5px]
\end{align}
Die Gewichtskraft ist folglich genauso groß wie die Auftriebskraft. Die Auftriebskraft selbst entspricht gemäß des archimedischen Prinzips der Gewichtskraft der verdrängten Flüssigkeit. Beim Treiben an der Oberfläche taucht ein Gegenstand folglich so tief ein, bis das Gewicht der verdrängten Flüssigkeit („Auftriebskraft“) dem Gewicht des Gegenstandes entspricht. Stellt man sich also das unterhalb der Oberfläche befindliche Volumen vollständig mit der umgebenden Flüssigkeit gefüllt vor, so entspricht dieses Gewicht dem Gewicht des Gegenstandes. Ein Schiff mit einer Masse von bspw. 50.000 Tonnen wird somit so tief einsinken, bis das eingetauchte Volumen 50.000 Tonnen Wasser verdrängt.

Ein Gegenstand taucht beim Treiben an der Oberfläche stets so tief ein, dass er so viel Flüssigkeit verdrängt wie er selbst schwer ist!
Die Eintauchtiefe eines Gegenstandes hängt also nicht nur von seiner eigenen Masse ab, sondern auch von der Dichte der umgebenden Flüssigkeit. Ein Schiff wird bspw. in Süßwasser einen stärkeren Tiefgang haben als in Meerwasser, d.h. tiefer eintauchen. Denn aufgrund der gelösten Salzes hat Meerwasser eine um ca. 3 % größere Dichte als Süßwasser. Das Schiff muss also stärker in das „leichtere“ Süßwasser eintauchen, um dieselbe Masse an Wasser zu verdrängen als im „schwereren“ Salzwasser.
Für Schiffe ist der maximal zulässige Tiefgang in Abhängigkeit des umgebenden Gewässers durch eine sogenannten Lademarke gekennzeichnet. Diese befindet sich seitlich am Schiffsrumpf. Die oberen zwei Striche zum Heck hin kennzeichnen dabei den erlaubten Tiefgang in allgemeinen Süßgewässern (F) bzw. im tropischen Süßwasser (TF). Die unteren vier Striche zum Bug hin geben den erlaubten Tiefgang in Salzwasser an, die tiefer liegen im Vergleich zu den Marken der Süßgewässer, da das Schiff dort größeren Auftrieb erfährt und deshalb stärker aus dem Wasser ragt. Unterschieden wird dabei zwischen tropischem Meerwasser (T), Seewasser im Sommer (S) bzw. im Winter (W) sowie zwischen Gewässern des Nordatlantiks im Winter (WNA).

Lademarken bei Schiffen geben die erlaubten Tiefgänge in Abhängigkeit des umgebenden Gewässers wieder!
Auch dieses Beispiel der Lademarke zeigt, dass Auftriebskraft offensichtlich umso stärker ist, je „schwerer“ die umgebende Flüssigkeit ist, d.h. umso größer die Dichte der Flüssigkeit. Dies wird letztlich auch direkt anhand von Gleichung (\ref{arch}) deutlich, in der die Flüssigkeitsdichte direkt die Auftriebskraft beeinflusst. Diese Eigenschaft zeigt sich bspw. deutlich auch beim Baden im Toten Meer. Aufgrund des sehr starken Salzgehaltes von teilweise über 30 % ist die Dichte des Wassers im toten Meer um ca. ein Viertel höher im Vergleich zum Süßwasser. Folglich ist die Auftriebskraft dort auch um rund 25 % größer als in Süßgewässern. Dies führt dazu, dass man im toten Meer praktisch ohne Zutun von alleine an der Oberfläche treibt und nicht unter geht.
Ausblick
Zwar wurden in diesem Artikel der Anschaulichkeit halber Flüssigkeiten betrachte, aber nicht nur dort sondern auch in Gasen wirken Auftriebskräfte, die letztlich auf derselben Ursache beruhen. Im Artikel Auftriebskraft in Gasen wird hierauf näher eingegangen.






