Das Moody-Diagramm ist eine graphische Darstellung der Rohrreibungszahl in Abhängigkeit der Reynolds-Zahl für ausgewählte Rauigkeiten der Rohrwand.
Druckverlust
Im Artikel Druckverlust in Rohrsystemen (Rohrreibungszahl) wurde auf den Druckverlust in Rohrleitungen und den damit verbundenen Formeln bereits ausführlich eingegangen. Deshalb sollen die Formeln an dieser Stell nur nochmal kurz zusammengefasst werden. Der Druckverlust ΔpV im Inneren eines Rohres mit dem Innendurchmesser \d und der Länge L ist von der Dichte des Fluids ϱ und der (mittleren) Strömungsgeschwindigkeit v abhängig:
\begin{align}
\label{def}
& \boxed{\Delta p_\text{V} = \lambda \cdot \frac{\rho}{2} \bar v^2 \cdot \frac{L}{ d}} ~~~\text{Druckverlust in einem geraden Rohrabschnitt} \\[5px]
\end{align}
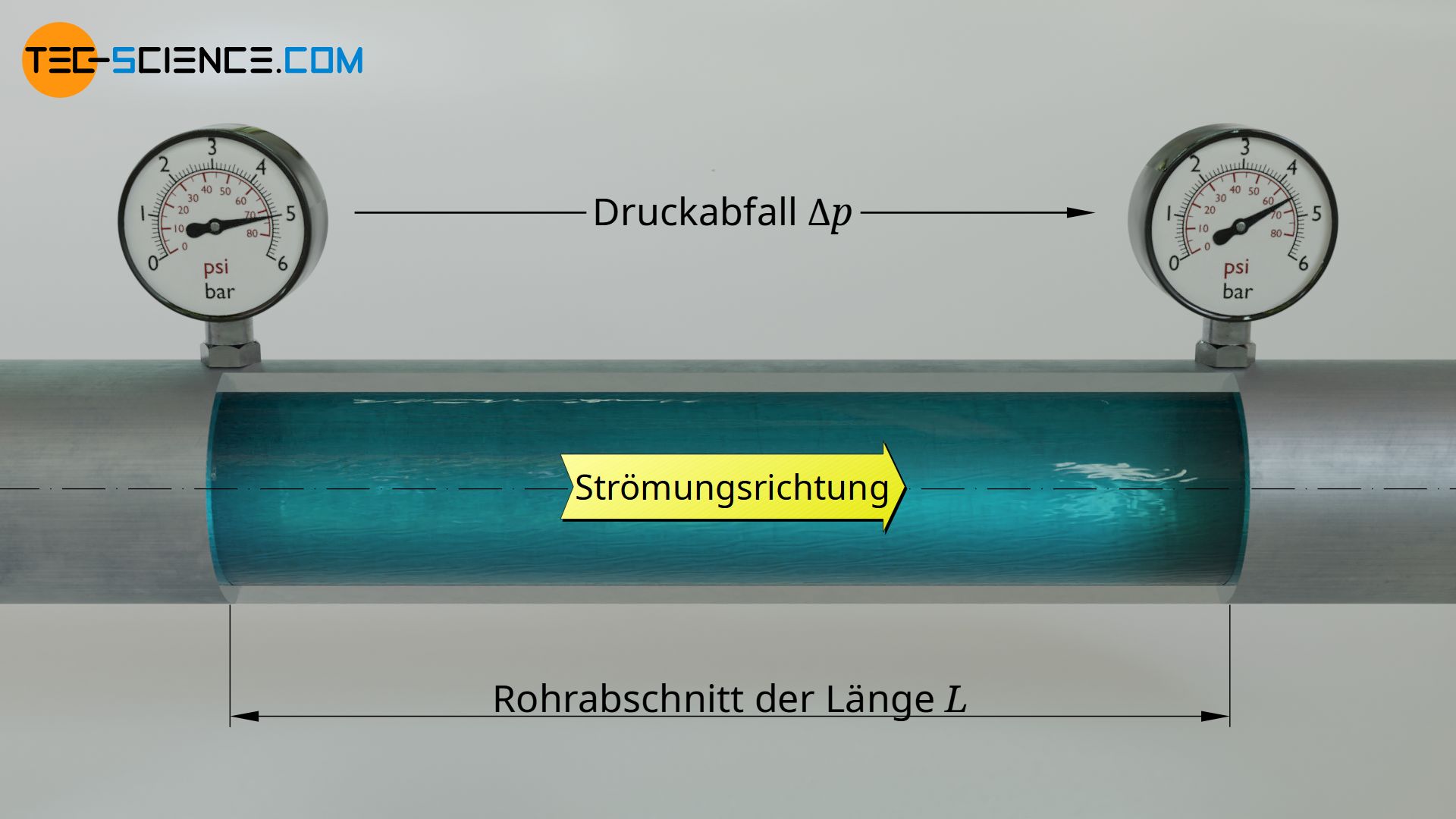
Der Einfluss der Strömung (laminar oder turbulent) und der Einfluss der Rauigkeit des Rohres auf den Druckverlust werden dabei durch die Rohrreibungszahl λ erfasst (auch Rohrwiderstandszahl oder Rohreibungskoeffizient genannt).
Der Druckverlust lässt sich auch in Abhängigkeit des Volumenstroms V* ausdrücken:
\begin{align}
\label{volu}
& \boxed{\Delta p_\text{V} = \lambda \cdot \frac{8\rho~}{\pi^2} \dot{V}^2 \cdot \frac{L}{d^5}} ~~~\text{Druckverlust in einem geraden Rohrabschnitt} \\[5px]
\end{align}
Rohrreibungszahl für laminare Strömungen
Für laminare Strömungen ist die Rohrreibungszahl nicht von der Rauigkeit der Rohrwand abhängig, sondern nur durch die Reynoldszahl Re bestimmt:
\begin{align}
\label{a}
&\boxed{\lambda_\text{lam}= \dfrac{64}{Re}} ~~~\text{Rohrreibungszahl bei laminarer Strömung}\\[5px]
&Re= \frac{v \cdot d \cdot \rho}{\eta}
\end{align}
Rohrreibungszahl für turbulente Strömungen
Bei turbulenten Strömungen ist der Einfluss der Rauigkeit der Rohrwand hingegen relativ groß. Die Rohrreibungszahl steigt mit zunehmender Rauheit und sinkt mit zunehmender Strömungsgeschwindigkeit. Bei hinreichend großen Reynoldszahlen wird die Rohrreibungszahl unabhängig der Strömungsgeschwindigkeit und ist damit nur noch von der Rauheit des Rohres abhängig. Die Rohrreibungszahl ist für turbulente Strömung durch die Colebrook-White Gleichung (\ref{cw}) gegeben:
\begin{align}
\label{cw}
&\boxed{\color{red}{\frac{1}{\sqrt{\lambda_\text{tur}}}}=-2\cdot \log_\text{10}\left(\frac{2,51}{Re} \cdot \color{red}{\frac{1}{\sqrt{\lambda_\text{tur}}}} +\frac{\varepsilon}{3,71}\right)} ~~~\text{Colebrook-White-Gleichung} \\[5px]
\end{align}
Darin bezeichnet ε die relative Rauheit der Rohrwand, d.h. das Verhältnis von Oberflächenrauheit und Rohrdurchmesser.
Als einfache Näherung kann die nachfolgend angegebene Haaland-Gleichung verwendet werden. Sie dient auch als Bestimmung des Startwertes für die iterative Lösung der Colebrook-White-Gleichung. Mehr zu diesem iterativen Lösungsverfahren der Colebrook-White-Gleichung im Artikel Druckverlust in Rohrsystemen (Rohrreibungszahl).
\begin{align}
&\boxed{\color{red}{\frac{1}{\sqrt{\lambda_\text{tur,0}}}}=-1,8\cdot \log_\text{10}\left(\frac{6,9}{Re} +\left(\frac{\varepsilon}{3,7}\right)^{1,11}\right)} ~~~\text{Haaland-Gleichung} \\[5px]
\end{align}
Für hydraulisch glatte Rohre, bei denen die viskose Unterschicht (laminare Unterschicht) die Oberflächenrauheiten vollständig überdeckt, ist die relative Rauheit null (ε=0). Die Colebrook-White-Gleichung lautet für diesen Spezialfall:
\begin{align}
&\boxed{\color{red}{\frac{1}{\sqrt{\lambda_\text{tur}}}}=-2\cdot \log_\text{10}\left(\frac{2,51}{Re} \cdot \color{red}{\frac{1}{\sqrt{\lambda_\text{tur}}}} \right)} ~~~\text{hydraulisch glatte Rohre} \\[5px]
\end{align}

Für hydraulisch raue Rohre, bei denen die Oberflächenrauheiten vollständig durch die viskose Unterschicht ragen, gilt nachfolgend angegebene Formel nach Nikuradse. Die Rohrreibungszahl ist dabei nicht mehr von der Reynoldszahl abhängig, sondern hauptsächlich durch die Wandrauigkeiten bestimmt.
\begin{align}
&\boxed{\color{red}{\frac{1}{\sqrt{\lambda_\text{tur}}}}=-2\cdot \log_\text{10}\left(\frac{\varepsilon}{3,71} \right)} ~~~\text{hydraulisch raue Rohre} \\[5px]
&\lambda_\text{tur}=\frac{1}{\sqrt{2\cdot \log_\text{10}\left(\frac{3,71}{\varepsilon} \right)}} \\[5px]
\end{align}
Beachte, dass zwar die Rohrreibungszahl mit zunehmender Reynoldszahl sinkt, dies aber nicht bedeutet, dass der Druckverlust hierdurch geringer werden würde. Der Druckverlust nimmt gemäß Gleichung (\ref{def}) nämlich mit dem Quadrat der Strömungsgeschwindigkeit zu. Der quadratische Einfluss der Strömungsgeschwindigkeit übersteigt also die geringer werdende Rohrreibungszahl um ein Vielfaches, sodass der Druckverlust grundsätzlich mit zunehmender Strömungsgeschwindigkeit ansteigt.
Moody-Diagramm
Das Moody-Diagramm gibt graphisch für verschiedene (relative) Wandrauigkeiten eines Rohres die Rohrreibungszahl in Abhängigkeit der Reynoldszahl (Strömungsart) wieder. Im Übergangsbereich zwischen laminarer und turbulenter Strömung ist eine verlässliche Angabe des Rohrreibungsbeiwertes allerdings nicht möglich.
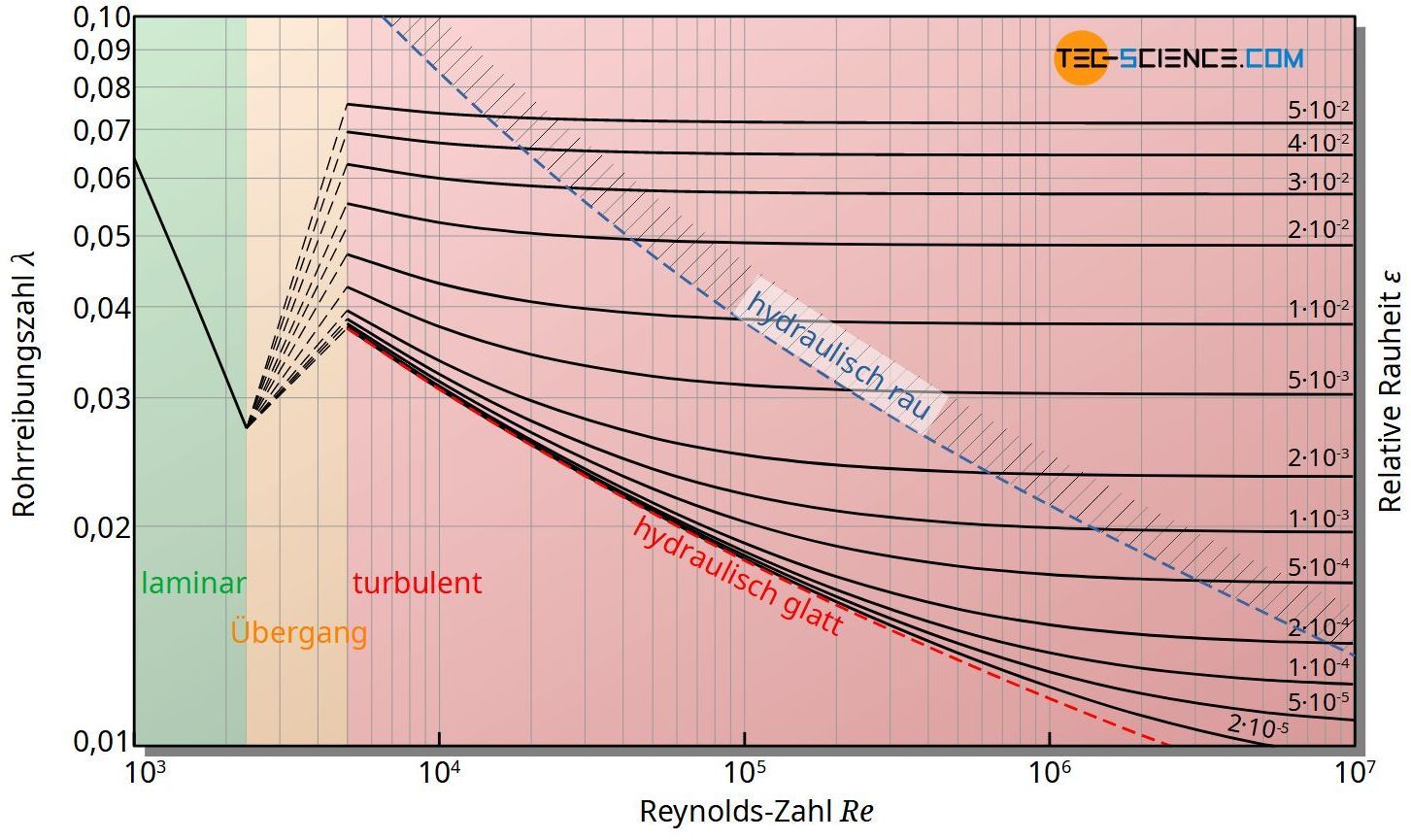
Die im Diagramm blau-gestrichelte Kurve markiert den Bereich der hydraulisch rauen Rohre, für die die Rohrreibungszahl unabhängig der Reynoldszahl ist. Für den hydraulisch rauen Bereich gilt folgende Ungleichung:
\begin{align}
&\boxed{\sqrt{\lambda}~Re~\varepsilon>200 } ~~~\text{für hydraulisch raue Rohre} \\[5px]
\end{align}






