Die Lewis-Zahl ist eine dimensionslose Ähnlichkeitskenngröße zur Beschreibung des Wärme- und Stofftransports.
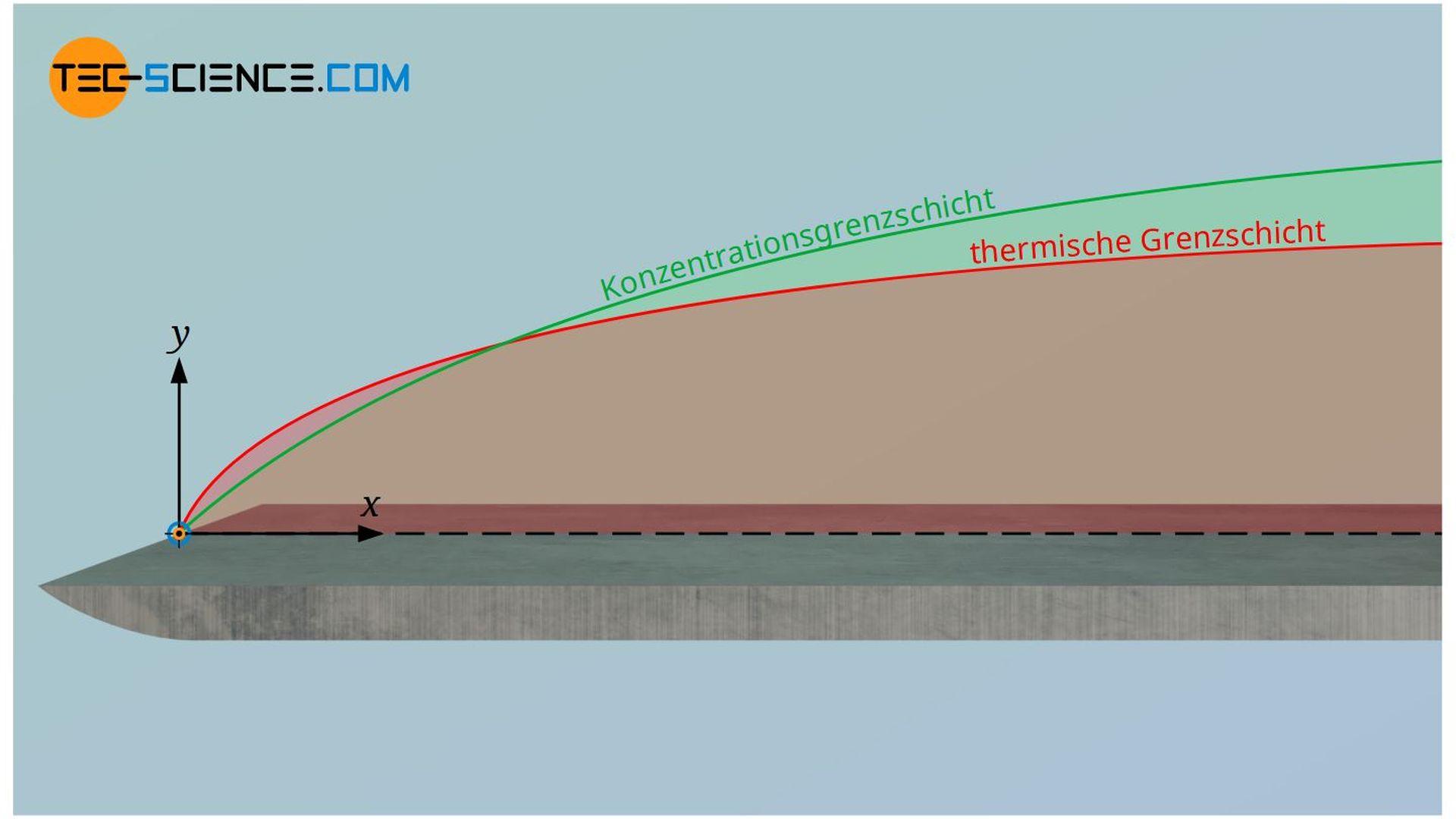
Die Lewis-Zahl kommt also immer dann ins Spiel, wenn in einem strömenden Fluid sowohl ein Wärmetransport durch Leitung als auch ein Stofftransport durch Diffusion vorliegt (Diffusion von Wärme und Stoff). Die Lewis-Zahl setzt sozusagen die Dicke der thermischen Grenzschicht ins Verhältnis zur Konzentrationsgrenzschicht. Sie bestimmt sich aus dem Verhältnis der Temperaturleitfähigkeit a und dem Diffusionskoeffizienten D:
\begin{align}
&\text{Lewis-Zahl}= \frac{\text{Wärmetransport}}{\text{Stofftransport}} \\[5px]
\label{le}
&\boxed{Le = \frac{a}{D}}=\frac{\lambda}{D \cdot c_p \cdot \rho} \\[5px]
\end{align}
Da sich die Temperaturleitfähigkeit definitionsgemäß au der Wärmeleitfähigkeit λ, der Dichte ϱ und der spezifischen Wärmekapazität cp berechnen lässt, kann sie auch über diese Größen ermittelt werden. Zudem lässt sich die Lewis-Zahl auch aus dem Verhältnis zwischen Schmidt-Zahl Sc und Prandtl-Zahl Pr ermitteln:
\begin{align}
&\boxed{Le = \frac{Sc}{Pr}} \\[5px]
\end{align}
Wärme- und Stofftransport sind in unterschiedlich großen Systemen nur dann physikalisch ähnlich, wenn die Lewis-Zahlen identisch sind. Auf diese Weise kann man anhand von verkleinerten Modellen dann Aussagen für das reale System treffen.
In der unteren Tabelle sind die dimensionslosen Kennzahlen im Überblick nochmals zusammengefasst. Im Artikel Dimensionslose Kennzahlen der Grenzschichten sind die Kennzahlen näher erläutert.
| Prandtl-Zahl Pr | Schmidt-Zahl Sc | Lewis-Zahl Le |
| Verhältnis von Impulstransport zu Energietransport | Verhältnis von Impulstransport zur Stofftransport | Verhältnis von Energietransport zur Stofftransport |
| \begin{align} \notag &\boxed{Pr = \frac{\nu}{a}}=\frac{\eta \cdot c_p}{\lambda} \\[5px] \end{align} | \begin{align} \notag &\boxed{Sc = \frac{\nu}{D}} =\frac{\eta}{\rho \cdot D}\\[5px] \end{align} | \begin{align} \notag &\boxed{Le = \frac{a}{D}}=\frac{\lambda}{\rho \cdot c_p \cdot D} \\[5px] \end{align} |






