Als Bernoulli-Effekt bezeichnet man die Abnahme des (statischen) Drucks in strömenden Fluiden mit zunehmender Strömungsgeschwindigkeit.
Druck als volumenspezifische Energie
Druck wird in der Einheit N/m² gemessen (Kraft pro Flächeneinheit). Erweitert man diesen Quotienten mit der Einheit Meter (m), dann lässt sich der Druck rein formal auch als Energie pro Volumen interpretieren:
\begin{align}
& [p] = \frac{\text{N}}{\text{m²}} \cdot \frac{\text{m}}{\text{m}} = \frac{\text{Nm}}{\text{m³}}=\frac{\text{J}}{\text{m³}} \\[5px]
\end{align}
Wie kann man sich den Druck als volumenspezifische Energie anschaulich vorstellen? Hierzu betrachten wir einen Wassertank, den wir mit einer Pumpe von unten mit einem Schlauch befüllen. Für das Befüllen des Tanks mit Wasser ist Arbeit erforderlich, da die im Tank befindliche Wassermasse entgegen der Schwerkraft nach oben gedrückt werden muss. Die hierfür notwendige Hubarbeit wird schließlich von der Pumpe aufgebracht.

Für den Pumpvorgang stellen wir uns eine von Hand betriebene Hubkolbenpumpe vor. Diese drückt mit einem Kolben die Wassermasse durch den Schlauch nach oben. Die für einen Pumpenhub notwendige Kraft können wir aus der Hublänge des Kolbens Δs und aus dem Druck p, der auf die Kolbenfläche A wirkt, bestimmen. Dabei gehen wir davon aus, dass der Tank ausreichend groß ist, sodass sich der Wasserspiegel bei einem Hub praktisch nicht ändert. In diesem Fall können wir während dem Hub von einer konstanten Kraft ausgehen. Für den Betrag der zugeführten Arbeit ΔW pro Hub gilt dann:
\begin{align}
& \Delta W = F \cdot \Delta s = p ~\underbrace{\cdot A \cdot \Delta s}_{\Delta V} \\[5px]
\label{w}
& \Delta W = p \cdot \Delta V \\[5px]
\end{align}
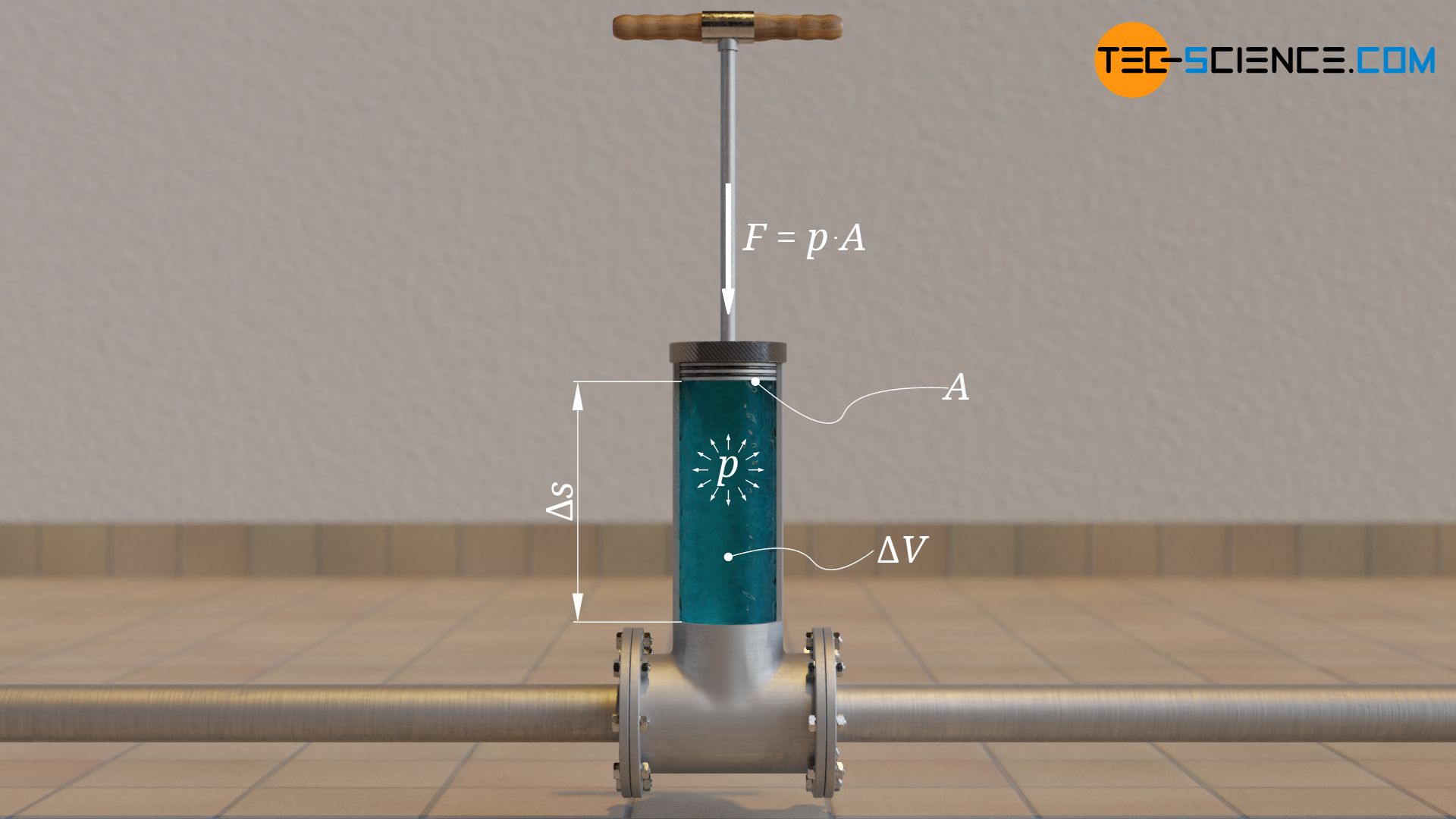
Das Produkt von Kolbenfläche und Hublänge entspricht gerade dem eingeschobenen Volumen ΔV. Die verrichtete Arbeit der Pumpe ΔW wurde während des Einschiebens in potentielle Energie des Fluids umgewandelt (Lageenergie). Drehen wir nun diesen Vorgang in Gedanken nun um. In diesem Fall drückt der Wasserdruck p den Kolben um die Strecke Δs zurück und verrichtet dann die Arbeit ΔW am Kolben. Das Fluidvolumen ΔV mit dem Druck p war offensichtlich in der Lage die Arbeit ΔW zu verrichten. Stellt man Gleichung (\ref{w}) um, dann mach der Druck offensichtlich auch eine Aussage wie viel Energie pro Volumen in einem Fluid vorhanden ist und entsprechend in Arbeit umgewandelt werden kann:
\begin{align}
\label{p}
& \boxed{p= \frac{\Delta W}{\Delta V}} \\[5px]
\end{align}
Der Druck lässt sich als volumenspezifische Energie auffassen (Energie pro Volumeneinheit), die angibt wie viel potentielle Energie in einem Volumen eines Fluids enthalten ist und in Arbeit umgewandelt werden kann!
Hydrodynamisches Paradoxon
Die energetische Interpretation des Drucks hat weitreichende Folgen. Betrachten wir hierzu ein Rohr durch das Wasser reibungsfrei strömt. An einem Reduzierstück wird da Rohr auf einen kleineren Durchmesser gebracht. Dieselbe Masse, die in das Reduzierstück einströmt, muss auch auf der reduzierten Seite wieder ausströmen, denn schließlich kann sich das Wasser im Reduzierstück nicht anhäufen oder vernichten werden (Kontinuitätsbedingung). Durch einen verkleinerten Querschnitt kann aber nur dann dieselbe Masse gefördert werden, wenn sich die Strömungsgeschwindigkeit entspricht erhöht. Genau dies geschieht innerhalb des Reduzierstücks, d.h. das strömende Fluid wird beschleunigt.
Die Beschleunigung bedeutet letztlich eine Erhöhung der kinetischen Energie des Fludis. Die Energie des Fluids kann sich aber nicht aus dem Nichts von selbst erhöhen (innerhalb des Reduzierstücks ist auch keine Pumpe eingebaut, die diese zusätzliche Energie hätte liefern können). Mit dem Wissen um die energetische Interpretation des Drucks, bleibt nur eine Antwort: Die Erhöhung der kinetischen Energie kann nur aus dem Druck stammen. Dies bedeutet aber auch, dass der Druck im verengten Abschnitt mit der höheren kinetischen Energie insgesamt geringer sein muss. Dass dies so ist, lässt sich durch angebrachte Druckmesser an den Rohren direkt bestätigen.
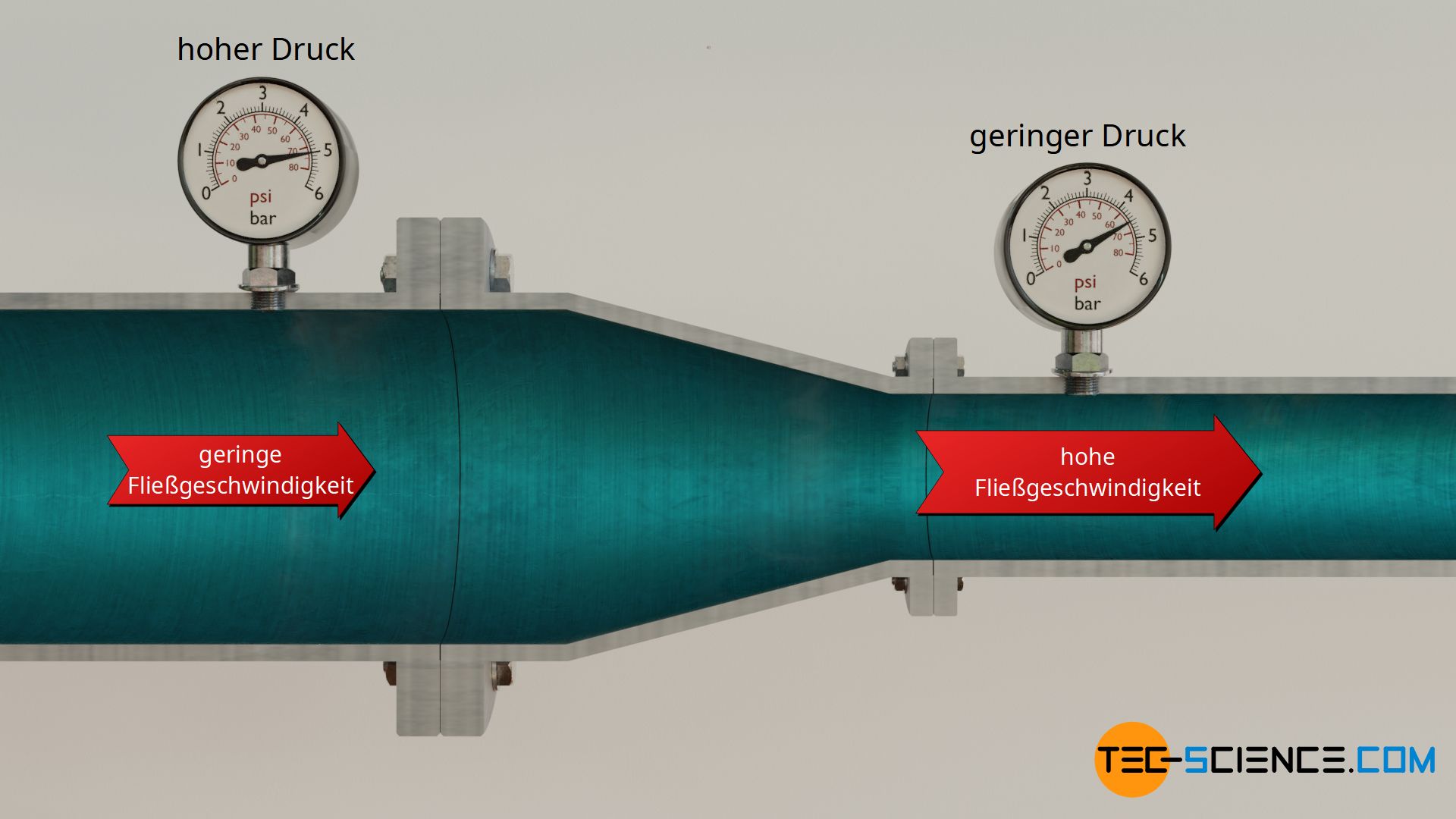
Entgegen der vermeintlichen Alltagserfahrung, sinkt also der Druck mit zunehmender Strömungsgeschwindigkeit. Warum es zu dieser missverständlichen Erfahrung kommt, erläutern wir später. Man bezeichnet dieses paradox erscheinende Phänomen der Druckabnahme bei Erhöhung der Strömungsgeschwindigkeit auch als hydrodynamisches Paradoxon, Bernoulli-Effekt oder Venturi-Effekt bezeichnet. Der Venturi-Effekt ist letztlich eine Konsequenz der Energieerhaltung.
Als Bernoulli-Effekt (Venturi-Effekt) bezeichnet man die Abnahme des statischen Drucks in strömenden Fluiden mit zunehmender Strömungsgeschwindigkeit!
Demonstration des Bernoulli-Effektes
Der Bernoulli-Effekt lässt sich eindrucksvoll an einem vertikalen Rohr demonstrieren, das an einer Platte mit Loch montiert ist. Eine weitere Platte mit zusätzlichem Gewicht wird von unten gegen diese Platte gehalten. Bläst man nun Luft durch das Rohr, so wird die untere Platte nicht etwa nach unten gedrückt, sondern nach oben! Grund hierfür ist der Bernoulli-Effekt. Durch den geringen Spalt zwischen den beiden Platten strömt die Luft sehr schnell. Der statische Druck zwischen den Platten sinkt. Somit wirkt an der Oberseite der unteren Platte ein geringer Druck als unten. Die Platte wird durch den größeren Umgebungsdruck an der Unterseite deshalb nach oben gedrückt.

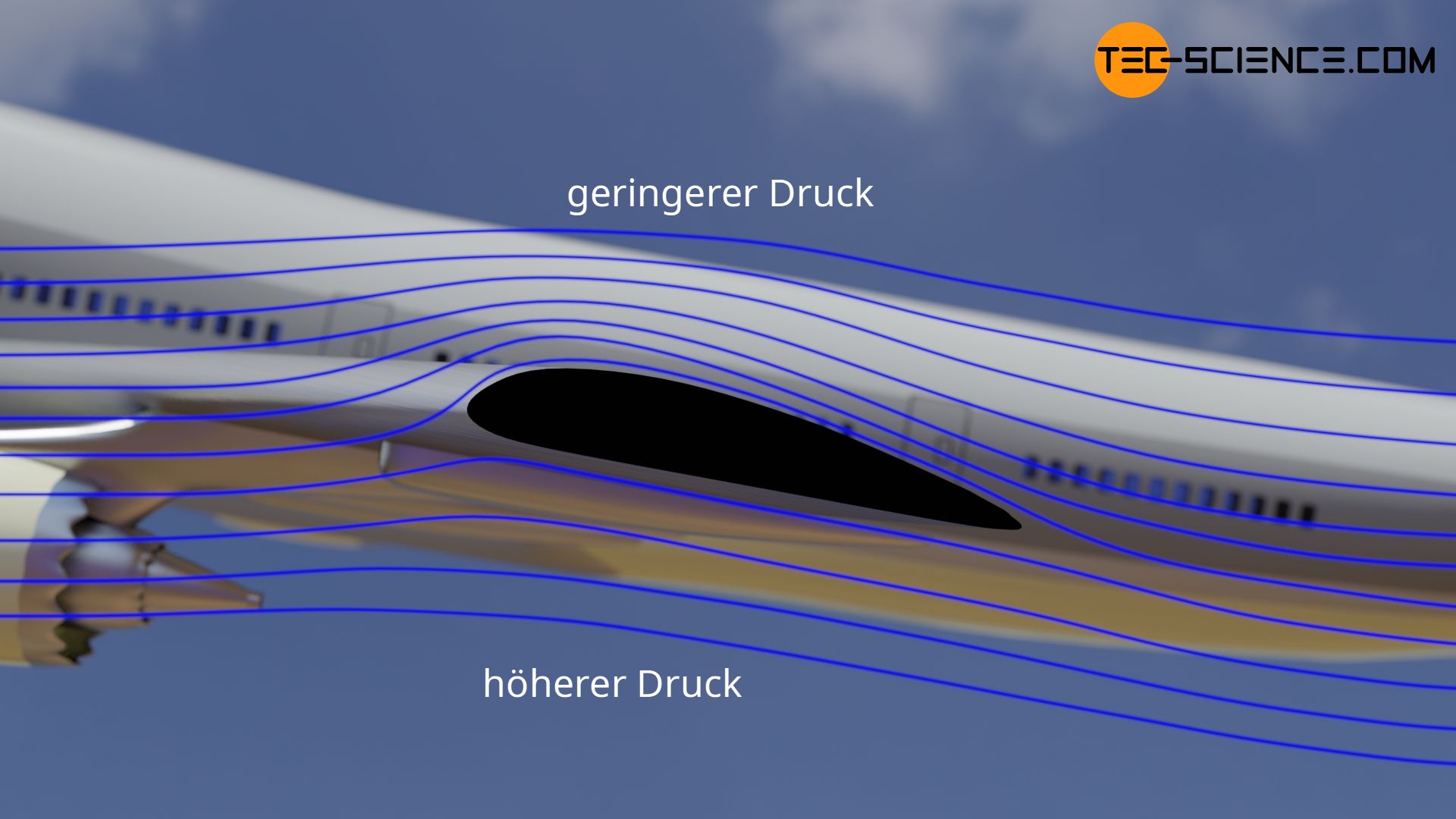
Auf die analoge Weise sorgt der der Bernoulli-Effekt an den Tragflächen von Flugzeugen für den entsprechenden Auftrieb. Auch Vergaser oder pneumatische Sauger sowie Dekanter arbeiten nach dem Bernoulli-Prinzip. Ebenfalls ist das Abdecken eines Daches bei Stürmen auf der windabgewandten Seite auf den Bernoulli-Effekt zurückzuführen. Im Artikel Beispiele und Anwendungen des Bernoulli-Effekts wird hierauf näher eingegangen.
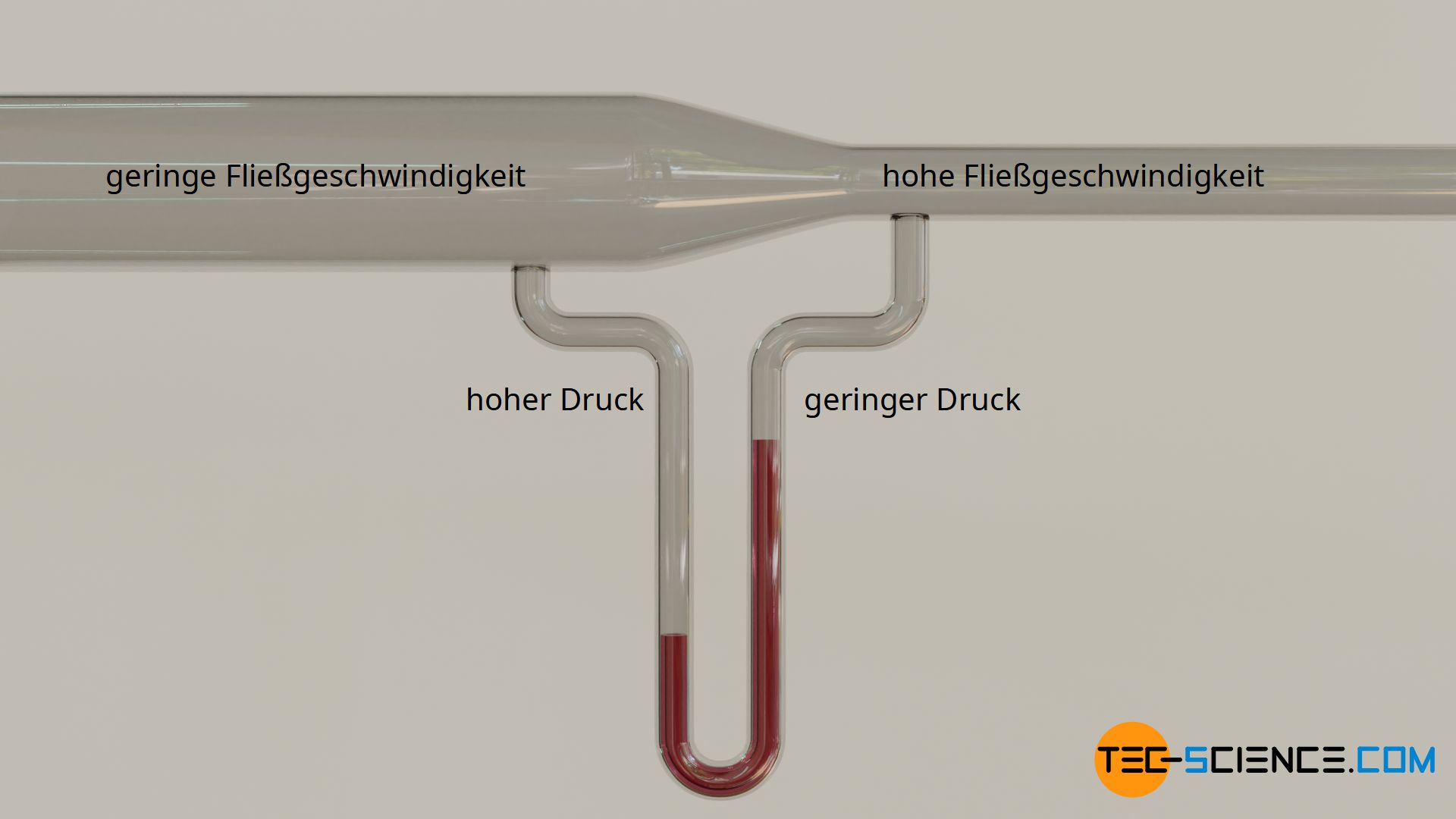
Venturi-Rohr und Laval-Düse
Anschaulich kann man den Druckabfall bei Zunahme der Strömungsgeschwindigkeit für Gasströmungen zeigen. Hierzu verbindet man die unterschiedlich großen Rohrabschnitte mit einem flüssigkeitsgefüllten U-Rohr. Der höhere Druck im Rohrabschnitt mit dem langsam strömenden Gas drückt die Flüssigkeitssäule in Richtung des geringeren Drucks im Rohrabschnitt mit dem schneller strömenden Gas. Eine solche Anordnung zur Erzeugung eines Druckunterschieds, insbesondere die Erzeugung eines Unterdrucks, wird auch als Venturi-Rohr oder Venturi-Düse bezeichnet. Mit Hilfe dieses Prinzips werden bspw. pneumatische Saugnäpfe betrieben.
Übrigens: Erreicht die Strömungsgeschwindigkeit in einem verengten Querschnitt eines Rohres die Schallgeschwindigkeit, so kann die Strömungsgeschwindigkeit im Überschallbereich nur dann weiter erhöht werden, wenn der Querschnitt wieder zunimmt. Das Rohr muss sich hierzu also wieder aufweiten. Man bezeichnet eine solche Rohrform auch als Laval-Düse. Die typische Verengung und anschließende Vergrößerung des Querschnitts zur Erzeugung von Überschallströmungen zeigt sich beispielsweise bei Triebwerken von Raketen. Der äußere sichtbare Teil des Raketentriebwerks bildet dabei den Überschallteil der Laval-Düse.

Woher kommt dieser scheinbare Widerspruch?
Woher kommt nun dieser scheinbare Widerspruch, dass der Druck bei zunehmenden Geschwindigkeiten abnimmt. Häufig stellt man sich in diesem Zusammenhang einen Wasserstrahl vor, der auf einen gerichtet ist. Dabei macht die Erfahrung deutlich: Je höher die Geschwindigkeit des Wasserstrahls ist, desto größer ist die Kraft und damit der Druck, den wir spüren. Diese Beobachtung ist zunächst nicht falsch, dafür aber die Schlussfolgerung!
Denn bei dieser Argumentation geht man fälschlicherweise davon aus, dass man den Druck in einem strömenden Zustand verspürt. Dies tut man aber nicht, denn der Flüssigkeitsstrahl wird beim Auftreffen abgebremst. Man verspürt den Druck im bereits abgebremsten Zustand sozusagen und nicht in einem strömenden Zustand!
Während beim Beschleunigen einer Strömung der Druck zu Gunsten der kinetischen Energie abnimmt, so steigt dieser beim Abbremsvorgang wieder an, d.h. kinetische Energie wird zurück in Druckenergie umgewandelt. Diese Druckerhöhung aufgrund der energetischen Umwandlung beim Abbremsen ist das was uns dazu verleiten lässt zu meinen, dass der statische Druck in strömenden Fluide höher ist. Tatsächlich beziehen wir uns bei dieser Argumentation aber auf den bereits abgebremsten Zustand.
Dasselbe gilt, wenn wir bspw. eine Platte in eine Wasserströmung halten und dann behaupten, der Druck nehme mit zunehmender Strömungsgeschwindigkeit zu. Den Druck, den wir dabei verspüren ist nicht der Druck im strömenden Zustand, sondern der Druck der bei der Abbremsung der Strömung an der Platte entsteht. Möchte man den statischen Druck in einem strömenden Fluid messen, dann darf die Strömung selbst dabei nicht abgebremst werden. Genau dies macht das Venturi-Rohr, indem der Druck sozusagen seitlich beim Vorbeiströmen gemessen wird. Dieses Prinzip wird auch zur Bestimmung des dynamischen Drucks mit Hilfe von Staudrucksonden (Prandtl-Rohr) angewendet.
Statischer, dynamischer und hydrostatischer Druck
Auch die im strömenden Fluid enthaltene kinetische Energie lässt sich auf das Volumen des Fluids beziehen. Gemäß Gleichung (\ref{p}) lässt sich somit auch der kinetischen Energie einen Druck zuordnen. In Abgrenzung zum statischen Druck in einem ruhenden Fluid bezeichnet man den mit der kinetischen Energie verbundenen Druck als dynamischen Druck. Die Zunahme des dynamischen Drucks (Zunahme der kinetischen Energie) erfolgt also zu Lasten des statischen Drucks.
Eine weitere statische Druckabnahme tritt zudem dann ein, wenn das Rohr nicht horizontal ausgerichtet ist, sondern schräg nach oben verläuft. Denn in diesem Fall muss das Fluid nicht nur beschleunigt werden, sondern zusätzlich entgegen der Schwerkraft nach oben gedrückt werden. Die hierfür aufzuwendende Hubarbeit bezieht die Strömung ebenfalls aus dem statischen Druck. Der statische Druck sinkt also weiter! Dieser Druckanteil, der auf das Aufbringen der Lageenergie entfällt wird als hydrostatischer Druck bezeichnet.
| Statischer Druck | Druckenergie Energie pro Volumen |
| Dynamischer Druck | kinetische Energie pro Volumen |
| hydrostatischer Druck | Lageenergie pro Volumen |
Der statische Druck kommt also salopp formuliert durch die ungeordnete Bewegung der Teilchen zustande, während der dynamische Druck durch die geordnete Bewegung der Moleküle zustande kommt (makroskopische Strömungsbewegung). Mathematisch beschrieben werden die Zusammenhänge zwischen Druckenergie (statischer Druck), kinetischer Energie (dynamischer Druck) und Lageenergie (hydrostatischer Druck) durch die Bernoulli-Gleichung. Im verlinkten Artikel wird hierauf näher eingegangen.






