Herleitung der erweiterten barometrischen Höhenformel (adiabatische Atmosphäre)

Die erweiterte barometrische Höhenformel berücksichtigt die Temperaturabnahme mit zunehmender Höhe und die damit verbundenen Auswirkungen auf den Luftdruck.

Klassische barometrische Höhenformel

Im Artikel Barometrische Höhenformel wurde die barometrische Höhenformel unter der Annahme einer konstanten Temperatur ausführlich hergeleitet. An dieser Stelle soll deshalb lediglich eine Kurzversion der Herleitung gegeben werden.

Betrachtet wird hierzu eine im Gleichgewicht mit der Umgebung stehende Luftschicht mit der infinitesimalen Dicke dh. Diese befinde sich in einer beliebigen Höhe h, in der die Luftdichte ϱ betrage. In diesem Fall hat man es letztlich mit drei Kräften zu tun, die gemeinsam im Gleichgewicht stehen. Zum einen wirkt ein Druck p auf die Unterseite der Luftschicht. Aufgrund der abnehmenden Luftdichte wirkt an der Oberseite hingegen ein geringer Luftdruck. Der Druck sei dort um einen Betrag dp geringer. Die entsprechenden Kräfte auf die beiden Seiten der Luftschicht lassen sich über das Produkt von Druck und Fläche A des Volumenelementes ermitteln. Als dritte Kraft wirkt schließlich die Gewichtskraft F_G der Luftschicht.

\begin{align}
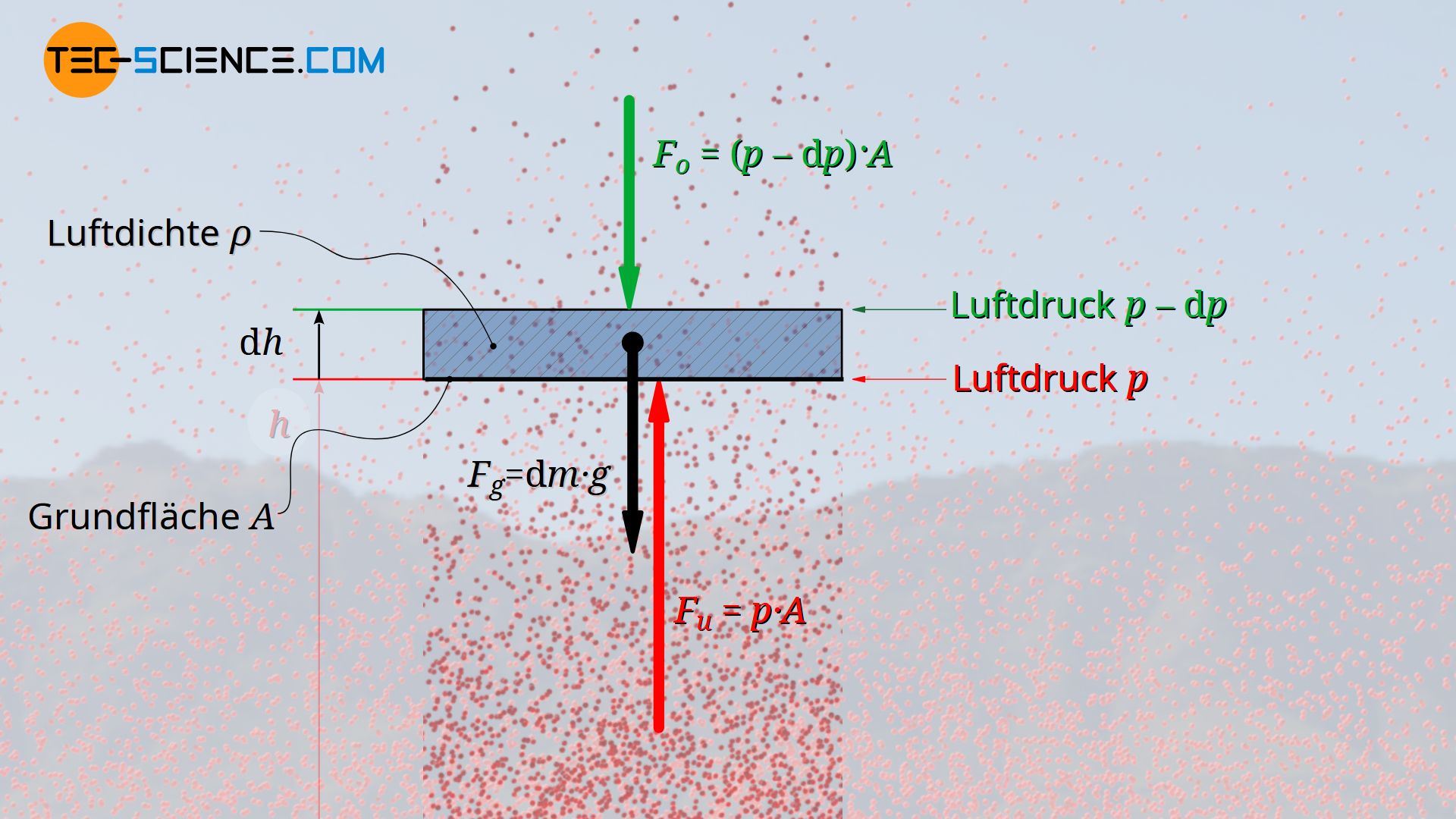
F_u &= p \cdot A &\text{Kraft an der Unterseite der Luftschicht} \\[5px]
F_o &= \left(p-\text{d} p \right) \cdot A &\text{Kraft an der Oberseite der Luftschicht} \\[5px]
F_G&= A \cdot \text{d} h \cdot \rho \cdot g &\text{Gewichtskraft der Luftschicht} \\[5px]
\end{align}

Die nach unten gerichtete Kraft des Luftdrucks auf der Oberseite der Luftschicht F_o und die ebenfalls nach unten wirkende Gewichtskraft F_G stehen somit mit der nach oben gerichteten Kraft an der Unterseite der Luftschicht F_u im Gleichgewicht.

\begin{align}
\require{cancel}
& F_u \overset{!}{=} F_G + F_o \\[5px]
& p \cdot \bcancel{A} = \bcancel{A} \cdot \text{d}h \cdot \rho \cdot g + \left(p-\text{d}p \right) \cdot \bcancel{A} \\[5px]
&\bcancel{p} = \text{d}h \cdot \rho \cdot g + \bcancel{p} – \text{d}p \\[5px]
&\text{d}p = \rho \cdot g \cdot \text{d}h \\[5px]
\end{align}

Um der Tatsache gerecht zu werden, dass sich der Druck mit zunehmender Höhe (dh>0) verringert und nicht erhöht (dp<0), wird in der oberen Gleichung noch ein Minuszeichen eingefügt:

\begin{align}
\label{dp}
&\boxed{\text{d}p =- \rho \cdot g \cdot \text{d}h} \\[5px]
\end{align}

Diese Gleichung lieft somit den Zusammenhang zwischen einer (infinitesimalen) Höhenänderung dh und der hieraus resultierenden (infinitesimalen) Druckänderung dp. Etwas störend zeigt sich an dieser Stelle jedoch die Tatsache, dass die Luftdichte selbst eine Funktion des Drucks ist. Denn je höher der Druck, desto stärker ist die Luft komprimiert und umso dichter ist sie. Es ist deshalb sinnvoll die Dichte als Funktion des Drucks auszudrücken. Dies lässt sich relativ einfach umsetzen, wenn man die Luft als ideales Gas betrachtet. Gemäß der thermischen Zustandsgleichung steht nämlich die Dichte über die Temperatur T wie folgt in Zusammenhang mit dem Druck (mit R_s als spezifische Gaskonstante):

\begin{align}
\label{ideal}
&p=R_s \cdot \rho \cdot T~~~~~\text{thermische Zustandsgleichung} \\[5px]
\label{rho}
&\boxed{\rho=\frac{p}{ R_s \cdot T }}\\[5px]
\end{align}

Wird Gleichung (\ref{rho}) in Gleichung (\ref{dp}) eingesetzt, so erhält man schließlich folgende Beziehung zwischen der (infinitesimalen) Höhenänderung und der hieraus resultierenden Druckänderung:

\begin{align}
\label{c}
&\boxed{\text{d}p = -\frac{g}{R_s \cdot T} \cdot p \cdot \text{d} h} \\[5px]
\end{align}

An dieser Stelle zeigt sich nun unmittelbar, dass die Druckänderung direkt vom herrschenden Luftdruck selbst beeinflusst wird. Die Druckänderung wird folglich umso geringer ausfallen, je niedriger der Druck ist (gleiche Höhenänderung dh vorausgesetzt). Es ist also davon auszugehen, dass der Luftdruck mit zunehmender Höhe weniger stark abfällt. Stellt man die Abnahme des Drucks über die Höhe dar, so erhält man folglich eine immer flacher werdende Kurve. Dadurch dass die Druckänderung proportional zum Druck ist, erhält man schließlich eine exponentielle Druckabnahme.

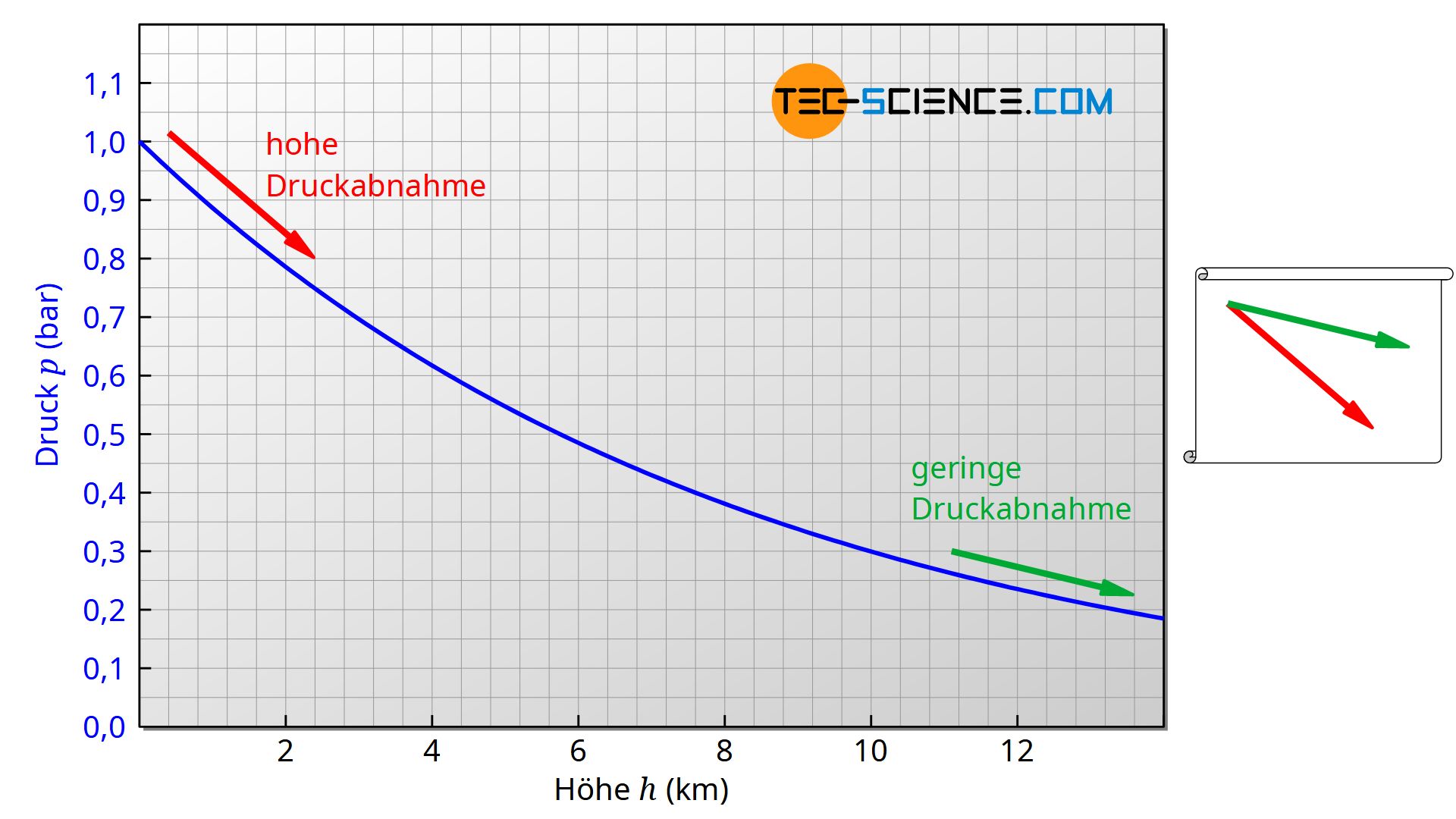
Man erhält diese Kurve durch Integration von Gleichung (\ref{c}), nachdem man die Variablen entsprechend trennt (Trennung der Variablen). Bei der Integration wird dabei von einer konstanten Temperatur ausgegangen. Als Ergebnis erhält man schließlich die klassische barometrische Höhenformel (die ausführliche Herleitung mit Erläuterungen dazu finden Sie im verlinkten Artikel):

\begin{align}
&\text{d}p = -\frac{g}{R_s \cdot T} \cdot p \cdot \text{d} h \\[5px]
&\frac{ \text{d}p }{p} = -\frac{g}{R_s \cdot T} \cdot p \cdot \text{d} h \\[5px]
&\int_{p_0}^{p}\frac{ \text{d}p }{p} =-\frac{g}{R_s \cdot T} \cdot \int_{0}^h \text{d} h \\[5px]
&\left[\ln{\left( p\right)}\right]_{p_0}^p = -\frac{g}{R_s \cdot T} \cdot \left[~h~\right]_{0}^{h}\\[5px]
& \ln{(p)}-\ln{(p_0)}= -\frac{g}{R_s \cdot T} \cdot {\left(h-0\right)}\\[5px]
& \ln{\left(\frac{p}{p_0}\right)}= -\frac{g \cdot h}{R_s \cdot T} \\[5px]
& \text{e}^{\Large{\ln{\left(\frac{p}{p_0}\right)}}}= \text{e}^{\Large{-\frac{g \cdot h}{R_s \cdot T} }}\\[5px]
&\frac{p}{p_0}= \text{e}^{-\frac{g \cdot h}{R_s \cdot T} }\\[5px]
\label{bar}
&\boxed{p(h)= p_0 \cdot \text{e}^{\Large{-\frac{g \cdot h}{R_s \cdot T}}}} ~~~~~\text{klassische barometrische Höhenformel} \\[5px]
\end{align}

In dieser Gleichung entspricht der Druck p₀ dem Druck auf einem beliebigen Bezugsniveau („Höhe Null“) und p dem Druck in der Höhe h über dem Bezugsniveau.

Einfluss des Temperaturverlaufs auf die barometrische Höhenformel (adiabate Atmosphäre)

Wie bereits erwähnt, wurde die barometrische Höhenformel gemäß Gleichung (\ref{bar}) unter der Bedingung einer konstanten Temperatur hergeleitet. Sie gilt also nur, wenn davon ausgegangen wird, dass sich die Temperatur der Atmosphäre mit der Höhe nicht ändert. Man spricht in diesem Zusammenhang deshalb auch von einer sogenannten isothermen Atmosphäre.

Die klassische barometrische Höhenformel gilt nur für eine isotherme Atmosphäre, d.h. unter der Bedingung, dass sich die Temperatur mit zunehmender Höhe nicht ändert.

Gerade bei Betrachtung großer Höhenänderungen zeigt die Praxis jedoch, dass die Temperatur nicht konstant bleibt, sondern meist mit zunehmender Höhe sinkt. Aus diesem Grund ist es auch auf hohen Bergen im Allgemeinen kälter als in den umliegenden Tälern. Dies lässt sich unter anderem darauf zurückführen, dass sich warme Luft die durch die Thermik nach oben steigt, aufgrund des geringer werdenden Drucks abkühlt. Ein solches Phänomen kann man auch bei Spraydosen beobachten. Das unter Druck stehende Gas wird sich stark abkühlen, wenn dieses ins Freie expandiert, d.h. auf einen geringeren Druck entspannt wird.

Für eine genauere Beschreibung des Druckverlaufs, muss man deshalb die Änderung der Temperatur berücksichtigen. Lässt man einen solchen Temperaturverlauf mit in die Herleitung der Druckverteilung einfließen, so spricht man von der erweiterten barometrischen Höhenformel.

Als erweiterte barometrische Höhenformel bezeichnet man die Berücksichtigung der Temperaturabnahme auf den Druckverlauf in der Atmosphäre.

Um den Temperaturverlauf zu modellieren, wird deshalb im Folgenden ein Luftpaket betrachtet, das nach oben steigt und sich aufgrund des geringeren werdenden Drucks ausdehnt und dabei abkühlt. Vereinfachend wird dabei angenommen, dass das Luftpaket keine Wärme an die Umgebung abgibt und auch keine von dieser aufnimmt. Es handelt sich also um ein adiabates System. Man spricht in diesem Zusammenhang deshalb auch von einer sogenannten adiabatischen Atmosphäre.

Zusammenhang zwischen Höhenänderung und Temperaturänderung (Temperaturgradient)

Beachte, dass nur weil bei einer adiabatischen Zustandsänderung keine Wärme übertragen wird, dies nicht bedeutet, dass sich die Temperatur nicht ändert. Die Temperaturänderung ist in diesem Fall ausschließlich auf die Druckänderung bzw. Volumenänderung während des Aufstiegs zurückzuführen und eben nicht auf eine externe Wärmeabfuhr, was die Modellierung entsprechend vereinfacht.

Für ein solches adiabatisches System bzw. für das als adiabat betrachtete Luftpaket, muss man also zunächst ein Zusammenhang zwischen einer Druckänderung (die mit der Höhenänderung verknüpft ist) und der hieraus resultierenden Temperaturänderung finden. Auf diese Weise kann man dann die Temperaturabnahme mathematisch beschrieben und anschließend in die barometrische Höhenformel einfließen lassen.

Hierfür ist zunächst der erste Hauptsatz der Thermodynamik in differentieller Schreibweise nötig. Dieser besagt ganz allgemein, dass eine (infinitesimale) Zufuhr von Arbeit dW und Wärme dQ zur Änderung der inneren Energie dU führt:

\begin{align}
&\boxed{\text{d}W + \text{d}Q = \text{d}U}~~~~~\text{Erster Hauptsatz der Thermodynamik} \\[5px]
\end{align}

Aufgrund des als adiabat vorausgesetzten Luftpakets wird in diesem Fall wird jedoch per Definition keine Wärme übertragen (dQ=0). Die Änderung der inneren Energie kommt also ausschließlich durch den Arbeitsumsatz zustande:

\begin{align}
\label{erst}
&\text{d}U = \text{d}W~~~~~\text{gilt für ein adiabates System} \\[5px]
\end{align}

Der Arbeitsumsatz ist dabei auf die Volumenvergrößerung des Luftpakets durch den geringer werdenden Druck zurückzuführen. Die Vergrößerung des Luftvolumens entgegen des herrschenden Luftdrucks erfordert Arbeit und wird deshalb auch als Volumenänderungsarbeit (oder Volumenarbeit) bezeichnet. Die Volumenarbeit ist bei gegebenem Luftdruck p nur von der Volumenänderung dV abhängig (das Minuszeichen in der unteren Gleichung resultiert aus der Konvention, dass bei einer Vergrößerung des Volumens Arbeit vom Gas verrichtet wird und deshalb negativ zu zählen ist):

\begin{align}
\label{dw}
&\boxed{\text{d}W = – p \cdot \text{d}V}~~~~~\text{Volumenänderungsarbeit} \\[5px]
\end{align}

Die für die Vergrößerung des Volumens benötigte Energie entstammt gemäß Gleichung (\ref{erst}) aus der inneren Energie, welche für ein ideales Gas der Masse m wiederum nur von der Temperaturänderung dT abhängig ist (mit c_v als spezifische Wärmekapazität des isochoren Prozesses):

\begin{align}
\label{du}
&\boxed{\text{d}U = c_v \cdot m \cdot \text{d}T}~~~~~\text{Änderung der inneren Energie} \\[5px]
\end{align}

Werden die Gleichungen (\ref{du}) und (\ref{dw}) in Gleichung (\ref{erst}) eingesetzt, dann zeigt sich, dass die Vergrößerung des Volumens (dV>0) in großen Höhen direkt eine Verringerung der Temperatur zur Folge hat (dT<0):

\begin{align}
& \text{d}W = \text{d}U \\[5px]
& c_v \cdot m \cdot \text{d}T = – p \cdot \text{d}V \\[5px]
\label{dt}
& \underline{\text{d}T = – \frac{p}{c_v \cdot m} \cdot \text{d}V } \\[5px]
\end{align}

Volumen, Druck und Temperatur wiederum stehen über die ideale Gasgleichung in Zusammenhang, die in diesem Fall nicht über die Dichte, sondern über das Volumen und die Masse des Luftpaketes ausgedrückt wird. Für die Temperatur gilt in Abhängigkeit des Drucks und des Volumens somit:

\begin{align}
\label{i}
& \boxed{p \cdot V = R_s \cdot m \cdot T}~~~~~\text{ideale Gasgleichung} \\[5px]
& T = \frac{p \cdot V}{R_s \cdot m} \\[5px]
\end{align}

Die Temperatur ändert sich also, sobald sich Druck und/oder Volumen ändern. In diesem Fall werden sich beide Größen ändern. Gemäß der Produktregel steht demnach eine infinitesimale Änderung der Temperatur dT wie folgt mit einer Druckänderung dp bzw. Volumenänderung dV in Zusammenhang („thermische Zustandsgleichung in differentieller Form“):

\begin{align}
& \text{d}T = \frac{\text{d}p \cdot V}{R_s \cdot m} + \frac{p \cdot \text{d}V}{R_s \cdot m} ~~~~~\text{ideale Gasgleichung in differentieller Form} \\[5px]
\end{align}

Wird diese Gleichung nach der Volumenänderung dV umgeformt, so kann diese direkt in Gleichung (\ref{dt}) eingesetzt werden:

\begin{align}
& \text{d}T = \frac{\text{d}p \cdot V}{R_s \cdot m} + \frac{p \cdot \text{d}V}{R_s \cdot m} \\[5px]
& R_s \cdot m \cdot \text{d}T = \text{d}p \cdot V + p \cdot \text{d}V \\[5px]
&\underline{\text{d}V= \frac{ R_s\cdot m\cdot\text{d}T}{p}- \frac{\text{d}p\cdot V}{p} } \\[5px]
\end{align}

Diese Gleichung in Gleichung (\ref{dt}) eingesetzt, ergibt folgender Zusammenhang zwischen einer infinitesimalen Druckänderung dp und der damit verbundenen Temperaturänderung dT:

\begin{align}
\require{cancel}
&\text{d}T = – \frac{p}{c_v \cdot m} \cdot \color{red}{\text{d}V} = – \frac{p}{c_v \cdot m} \cdot \color{red}{\left( \frac{ R_s\cdot m\cdot\text{d}T}{p}- \frac{\text{d}p\cdot V}{p} \right) } \\[5px]
& \text{d}T =-\frac{R_s \cdot \bcancel{m} \cdot \text{d}T \cdot \bcancel{p}}{c_v \cdot \bcancel{m} \cdot \bcancel{p}}
+ \frac{\bcancel{p} \cdot \text{d}p \cdot V}{c_v \cdot m \cdot \bcancel{p}} \\[5px]
& \text{d}T =-\frac{R_s \cdot \text{d}T}{c_v}+\frac{\text{d}p \cdot V}{c_v \cdot m} \\[5px]
& \text{d}T \cdot c_v =-R_s \cdot \text{d}T+\frac{V}{m} \cdot \text{d}p\\[5px]
&\text{d}T \cdot (c_v+R_s) =\frac{V}{m} \cdot \text{d}p\\[5px]
\end{align}

An dieser Stelle kann ausgenutzt werden, dass die Summe aus spezifischer Wärmekapazität c_v und spezifischer Gaskonstante R_s gerade der spezifischen Wärmekapazität für den isobaren Prozess c_p entspricht. Zudem kann der Quotient V/m gemäß der thermischen Zustandsgleichung (\ref{i}) durch den Ausdruck R_s⋅T/p ersetzt werden. Somit zeigt sich folgender Zusammenhang zwischen einer Druckänderung dp bei gegebenem Druck p und der hieraus resultierenden Temperaturänderung dT bei gegebener Temperatur T:

\begin{align}
&\text{d}T \cdot \underbrace{(c_v+R_s)}_{c_p} =\underbrace{\frac{V}{m}}_{ \frac{R_s \cdot T}{p} } \cdot \text{d}p\\[5px]
&\text{d}T \cdot c_p=\frac{R_s \cdot T}{p} \cdot \text{d}p \\[5px]
\label{zz}
&\boxed{\frac{\text{d}T}{T} =\frac{R_s}{c_p} \cdot \frac{\text{d}p}{p}} \\[5px]
\end{align}

Die obere Gleichung (\ref{zz}) beschreibt die Temperaturänderung bei einer Druckänderung. In diesem Fall soll jedoch die Temperaturänderung nicht anhand der Druckänderung beschrieben werden, sondern durch die Höhenänderung. Hierzu wird Gleichung (\ref{c}) benötigt, die die Druckänderung dp mit der Höhenänderung dh verknüpft:

\begin{align}
\require{cancel}
& \frac{\text{d}T}{T}=\frac{R_s}{c_p}\cdot\frac{\overbrace{-\frac{g}{R_s \cdot T} \cdot p \cdot \text{d} h}^{\text{d}p} }{p}\\[5px]
& \frac{\text{d}T}{ \bcancel{T}}=-\frac{ \bcancel{R_s} \cdot g \cdot \bcancel{p} \cdot \text{d}h}{c_p \cdot \bcancel{R_s} \cdot \bcancel{T} \cdot \bcancel{p}}\\[5px]
\label{grad}
&\boxed{\frac{\text{d}T}{ \text{d}h } = -\frac{g}{c_p}}:=\Gamma ~~~~~\text{Temperaturgradient} \\[5px]
\end{align}

In dieser Form beschreibt die obere Gleichung die Temperaturänderung dT pro Höhenänderung dh, d.h. die Temperaturabnahme in Kelvin pro Meter Höhe. Dieser Ausdruck wird auch Temperaturgradient Γ genannt. Wie die obere Gleichung zeigt, ergibt sich der Temperaturgradient lediglich aus Konstanten. In der als adiabat angenommenen Atmosphäre erhält man also eine lineare Abnahme der Temperatur.

Für trockene Luft mit einer spezifischen Wärmekapazität von c_p=1005 J/(kg⋅K) ergibt sich auf diese Weise eine Temperaturabnahme von etwa 1 Kelvin (1 °C) pro 100 Metern Höhe:

\begin{align}
&\Gamma = -\frac{g}{c_p} = -\frac{9,81 \frac{\text{N}}{\text{kg}} }{ 1005 \frac{\text{ J}}{\text{kg K}} } \approx \underline{\underline{\frac{ – 1 \text{K}}{100 \text{ m}}}}\\[5px]
\end{align}

Unter Annahme einer adiabaten Atmosphäre nimmt bei trockener Luft die Temperatur linear um rund 1 °C pro 100 Meter Höhe ab (trockenadiabatischer Temperaturgradient genannt)!

Kennt man folglich die Temperatur T₀ auf Bezugsniveau, dann lässt sich die Temperatur T in einer beliebigen Höhe h hierzu wie folgt bestimmen:

\begin{align}
\label{th}
&\boxed{T(h) = T_0 + \Gamma \cdot h} ~~~\text{mit}~~~ \boxed{\Gamma=-\tfrac{g}{c_p}} \\[5px]
\end{align}

Alternative Herleitung des Temperaturgradienten

Eine alternative Herleitung des Temperaturgradienten geht von der Adiabatengleichung aus, die wie folgt Druck und Temperatur zweier Zustände miteinander verknüpft (mit κ als Adiabatenkoeffizient: κ=c_p/c_v):

\begin{align}
& T_1^{\kappa} \cdot p_1^{1-\kappa} = T_2^{\kappa} \cdot p_2^{1-\kappa} \\[5px]
& \left(\frac{T_2}{T_1}\right)^{-\kappa} = \left(\frac{p_2}{p_1}\right)^{1-\kappa} \\[5px]
\end{align}

Logarithmiert man nun beide Seiten der Gleichung und nutzt die Tatsache, dass der logarithmierte Quotient auch also eine Subtraktion geschrieben werden kann, dann folgt:

\begin{align}
&\ln\left[\left(\frac{T_2}{T_1}\right)^{-\kappa}\right] = \ln\left[\left(\frac{p_2}{p_1}\right)^{1-\kappa}\right] \\[5px]
& -\kappa \cdot \ln\left(\frac{T_2}{T_1}\right) = (1-\kappa) \cdot \ln\left(\frac{p_2}{p_1}\right) \\[5px]
&-\kappa \cdot \left[\ln\left(T_2\right) – \ln\left(T_2\right) \right] = (1-\kappa) \cdot \left[ \ln\left(p_2\right) – \ln\left(p_1\right) \right] \\[5px]
\end{align}

Diese Gleichung kann man schließlich über folgende Integration erhalten:

\begin{align}
&-\kappa \cdot \int_{T_1}^{T_2} \frac{1}{T}~ \text{d}T= (1-\kappa) \cdot \int_{p_1}^{p_2} \frac{1}{p} ~ \text{d}p \\[5px]
\end{align}

Leitet man beide Seiten nun entsprechend ab, dann fallen die Integralzeichen im Prinzip einfach weg. Man erhält auf diese Weise folgenden differentiellen Zusammenhang zwischen einer Druckänderung und der hieraus resultierenden Temperaturänderung:

\begin{align}
&-\kappa \cdot \frac{1}{T} ~\text{d}T = (1-\kappa) \cdot \frac{1}{p} ~ \text{d}p \\[5px]
\label{z}
&\boxed{ \frac{ \text{d}T }{T} ~ = \frac{\kappa-1}{\kappa} \cdot \frac{\text{d}p}{p} } \\[5px]
\end{align}

Da der Adiabatenexponent κ per Definition dem Verhältnis der Wärmekapazitäten c_p/c_v entspricht, kann der Ausdruck (κ-1)/κ auch wie folgt geschrieben werden:

\begin{align}
\frac{\kappa-1}{\kappa}&= \frac{\tfrac{c_p}{c_v} -1}{\tfrac{c_p}{c_v}} ~~~\text{multiplizieren mit }\tfrac{c_v}{c_v} \text{ liefert:} \\[5px]
&= \frac{c_p-c_v}{c_p} ~~~\text{mit } c_p-c_c = R_s \text{ folgt:} \\[5px]
& = \frac{R_s}{c_p} \\[5px]
\end{align}

Ersetzt man also in Gleichung (\ref{z}) den Ausdruck (κ-1)/κ durch den soeben hergeleiteten Term R_s/c_p, dann erhält man schließlich dieselbe Gleichung wie bereits im Abschnitt zuvor [siehe Gleichung (\ref{zz})]:

\begin{align}
&\boxed{\frac{\text{d}T}{T} =\frac{R_s}{c_p} \cdot \frac{\text{d}p}{p}} \\[5px]
\end{align}

Die weitere Herleitung des Temperaturgradienten ist nun wieder identisch mit der Herleitung im Abschnitt zuvor. Hierzu ist wiederum die Druckänderung nach Gleichung (\ref{c}) zu verwenden und in die obere Gleichung einzusetzen:

\begin{align}
\require{cancel}
& \frac{\text{d}T}{T}=\frac{R_s}{c_p}\cdot\frac{\overbrace{-\frac{g}{R_S \cdot T} \cdot p \cdot \text{d} h}^{\text{d}p} }{p}\\[5px]
& \frac{\text{d}T}{ \bcancel{T}}=-\frac{ \bcancel{R_s} \cdot g \cdot \bcancel{p} \cdot \text{d}h}{c_p \cdot \bcancel{R_s} \cdot \bcancel{T} \cdot \bcancel{p}}\\[5px]
\label{grad2}
&\boxed{\frac{\text{d}T}{ \text{d}h } = -\frac{g}{c_p}} \\[5px]
\end{align}

Einfluss der Luftfeuchtigkeit auf den Temperaturgradienten

Der oben ermittelte Temperaturgradient von rund -1 K/(100m) gilt strenggenommen nur für trockene Luft, die kein gasförmiges Wasser gebunden hat. Man spricht deshalb auch vom sogenannten trockenadiabatischen Temperaturgradienten.

In der Realität enthält die Luft jedoch immer zu einem gewissen Grad Feuchtigkeit, d.h. es befindet sich gasförmiges Wasser in der Luft (Wasserdampf genannt). Dementsprechend ändert sich auch die spezifische Wärmekapazität c_p und mit ihr der Temperaturgradient. Tatsächlich bleibt der Einfluss der geänderten Wärmekapazität auf den Temperaturgradienten jedoch häufig vernachlässigbar gering, da nur etwa 1 % Wasserdampf in der Luft enthalten ist.

Deutlich größeren Einfluss auf den Temperaturgradienten hat eine mögliche Kondensation des im Luftpaket enthaltenen Wasserdampfes. Mit sinkender Temperatur wird es nämlich irgendwann dazu kommen, dass ein Teil des gasförmig gebundenen Wassers kondensiert, d.h. wieder flüssig wird. Dies liegt daran, dass kalte Luft weniger Wasser speichern kann als warme Luft. Bei 20 °C ist in einem Kubikmeter Luft maximal ca. 17 g Wasserdampf enthalten; bei -20 °C hingegen nur rund 1 g.

Sinkt die Temperatur nun mit zunehmender Höhe, dann kann das aufsteigende Luftpaket das darin enthaltene Wasser irgendwann nicht mehr vollständig in sich speichern. Es kommt in der Folge zur Kondensation des Wassers und es scheiden sich aus dem übersättigten Luftpaket flüssige Wassertröpfchen aus. In diesem Zustand entspricht die Lufttemperatur exakt dem Taupunkt.

Die Kondensation des Wassers kann man sehr gut als Wolkenbildung beobachten. Die Höhe, wo die Kondensation und damit die Wolkenbildung stattfindet, wird auch als Kondensationsniveau oder als Wolkenbasis bezeichnet. In welcher Höhe sich die Wolkenbasis befindet, hängt stark von der Umgebung und den Wetterbedingungen ab. Die Wolkenbasis kann sich bspw. in einer Höhe von 3 km bilden, aber auch direkt über dem Boden können sich Wolken bilden; dieses Phänomen wird dann als Nebel bezeichnet.

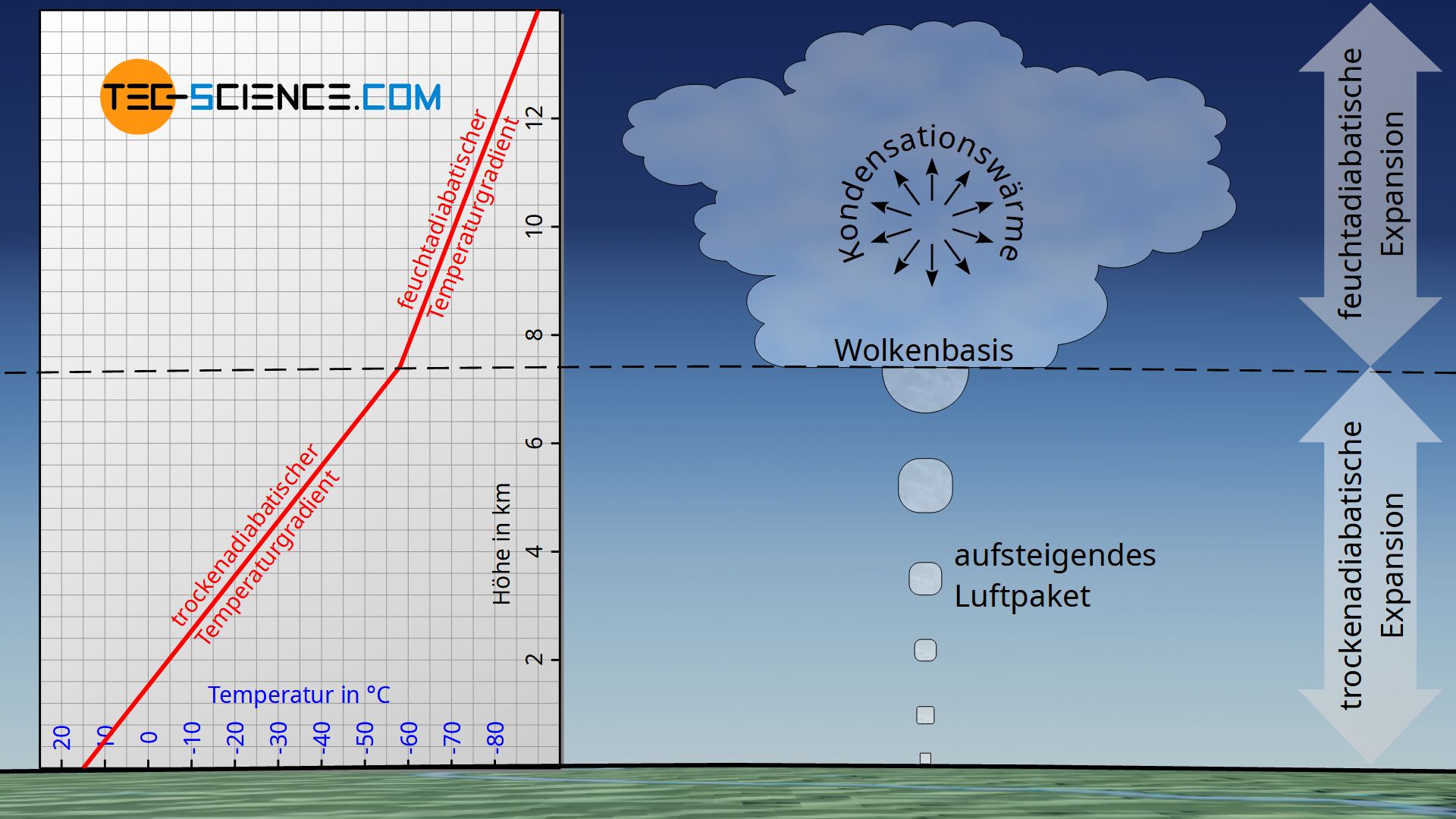
Die Wolkenbildung ist aus thermodynamischer Sicht von einem wichtigen Phänomen begleitet. Die während der Kondensation des Wassers freiwerdende Kondensationswärme (auch latente Wärme genannt) wirkt nämlich der Abkühlung der Luft entgegen. Oberhalb der Wolkenbasis kühlt also ein aufsteigendes Luftpaket nicht mehr so stark ab wie dies unterhalb der Wolkenbasis der Fall ist. Folglich ist der Temperaturgradient während der Kondensation betragsmäßig geringer als ohne Wolkenbildung. Demzufolge unterscheidet man auch zwischen dem trocken-adiabatischen Temperaturgradienten (ohne Kondensation) und dem feucht-adiabatischen Temperaturgradienten (mit Kondensation).

Im Gegensatz zum trockenadiabatischen Temperaturgradienten berücksichtigt der feuchtadiabatische Temperaturgradient die Kondensation des Wasserdampfes mit zunehmender Höhe! Der feuchtadiabatische Temperaturgradient ist aufgrund der freiwerdenden Kondensationswärme betragsmäßig geringer als der trockenadiabatische.

Für die sogenannte Standardatmosphäre wird der feuchtadiabatische Temperaturgradient auf den ersten 11 km über Meereshöhe mit 0,65 °C/100m angenommen. Zur Standardatmosphäre später in einem eigenen Abschnitt mehr dazu.

Erweiterte barometrische Höhenformel bezüglich des Drucks

Da nun der Temperaturverlauf in Abhängigkeit der Höhe gemäß Gleichung (\ref{th}) bekannt ist, kann man diesen in der Herleitung des Druckverlaufs ausgehend der Gleichung (\ref{c}) berücksichtigen.

\begin{align}
&\text{d}p = -\frac{g}{R_s \cdot T(h)} \cdot p \cdot \text{d} h \\[5px]
&\text{d}p = -\frac{g}{R_s \cdot \left(T_0 + \Gamma \cdot h \right)} \cdot p \cdot \text{d} h \\[5px]
&\frac{\text{d}p}{p} = -\frac{g}{R_s} \cdot \frac{\text{d} h}{ T_0 +\Gamma \cdot h } \\[5px]
\end{align}

Beide Seiten können nun innerhalb der entsprechenden Grenzen integriert werden. Die unteren Grenzen beziehen sich dabei auf das Bezugsniveau mit der definitionsgemäßen Höhe h₀=0 und dem dort herrschenden Bezugsdruck p₀. Die obere Integrationsgrenze bildet die betrachtete Höhe h in der der Druck p ermittelt werden soll.

\begin{align}
\label{p0}
&\boxed{\int_{p_0}^p~\frac{\text{d}p}{p} = -\frac{g}{R_s} \cdot \int_{h_0=0}^h\frac{\text{d} h}{T_0+\Gamma \cdot h}} \\[5px]
\end{align}

Die linke Seite dieser Gleichung ergibt den bereits bekannten Ausdruck ln(p/p₀) [siehe Herleitung von Gleichung (\ref{bar})]. Für die Lösung des Integrals auf der rechten Seite dieser Gleichung hilft ein Blick in die Formelsammlung der Mathematik. Für den allgemeinen Fall einer linearen Funktion im Nenner eines Bruches ergibt sich folgendes unbestimmtes Integral:

\begin{align}
&\int \frac{\text{d}x}{b+a \cdot x} = \frac{1}{a} \cdot \ln\left(b+a\cdot x\right) \\[5px]
\end{align}

Diese Lösung lässt sich nun auf unseren Fall übertragen. Mit x=h, b=T₀ und a=Γ, ergibt sich für das Integral auf der linken Seite von Gleichung (\ref{p0}) folgende Lösung:

\begin{align}
\int_{0}^h\frac{\text{d} h}{T_0 +\Gamma \cdot h} &= \left[\frac{1}{\Gamma} \cdot \ln\left(T_0+\Gamma \cdot h\right) \right]^h_0 \\[5px]
&= \frac{1}{\Gamma} \cdot \ln\left(T_0+\Gamma \cdot h\right) – \frac{1}{\Gamma} \cdot \ln\left(T_0\right) \\[5px]
&= \frac{1}{\Gamma} \cdot \left[ \ln\left(T_0+\Gamma \cdot h\right) -\ln\left(T_0\right)\right] \\[5px]
&= \frac{1}{\Gamma} \cdot \ln\left(\frac{T_0+\Gamma \cdot h}{T_0}\right) \\[5px]
& = \frac{1}{\Gamma} \cdot \ln\left(1+\frac{\Gamma}{T_0} \cdot h\right) \\[5px]
\end{align}

Gleichung (\ref{p0}) stellt sich insgesamt also wie folgt dar:

\begin{align}
\color{red}{\int_{p_0}^p~\frac{\text{d}p}{p}} &= -\frac{g}{R_s} \cdot \color{blue}{\int_{h_0=0}^h\frac{\text{d} h}{T_0 +\Gamma \cdot h}} \\[5px]
\color{red}{\ln\left(\frac{p}{p_0}\right) } &= -\frac{g}{R_s} \cdot \color{blue}{ \frac{1}{\Gamma} \cdot \ln\left(1+\frac{\Gamma}{T_0} \cdot h\right) } \\[5px]
\end{align}

Diese Gleichung lässt sich nach dem gesuchten Druck p auflösen, wenn man zunächst die e-Funktion auf beiden Seiten anwendet und anschließend die Gleichung unter Zuhilfenahme verschiedener Logarithmengesetze vereinfacht (z.B.: e^ln(x)=x und \(\text{e}^{a \cdot b}= \left(\text{e}^{a}\right)^b\)):

\begin{align}
\text{e}^{\ln\left(\frac{p}{p_0}\right)} &= \text{e}^{-\frac{g}{R_s \cdot \Gamma} \cdot \ln\left(1+\frac{\Gamma}{T_0} \cdot h\right)}\\[5px]
\frac{p}{p_0} &= \left(\text{e}^{\ln\left(1+\frac{\Gamma}{T_0} \cdot h\right)} \right)^{ -\frac{g}{R_s \cdot \Gamma }}\\[5px]
\frac{p}{p_0} &= \left(1+\frac{\Gamma}{T_0} \cdot h\right)^{ -\frac{g}{R_s \cdot \Gamma }} \\[5px]
\end{align}

\begin{align}
\label{ext}
&\boxed{p(h) = p_0 \cdot \left(1+\frac{\Gamma}{T_0} \cdot h\right)^{ -\frac{g}{R_s \cdot \Gamma }}}~~~\text{barometric formula for an adiabatic atmosphere} \\[5px]
\end{align}

Die obere Gleichung gibt unter Berücksichtigung eines linearen Temperaturverlauf den Druck in einer beliebigen Höhe h über einem Bezugsniveau wieder. Diese Formel wird erweitere barometrische Höhenformel genannt. Beachte, dass der Temperaturgradient Γ in dieser Gleichung negativ einzusetzen. Der Temperaturgradient muss dabei in der Einheit K/m („Kelvin pro Meter“) angegeben werden und die Temperatur T₀ in Kelvin. Der Druck p₀ kann in der üblichen Einheit bar belassen werden; die berechneten Drücke p sind dann ebenfalls in der Einheit bar.

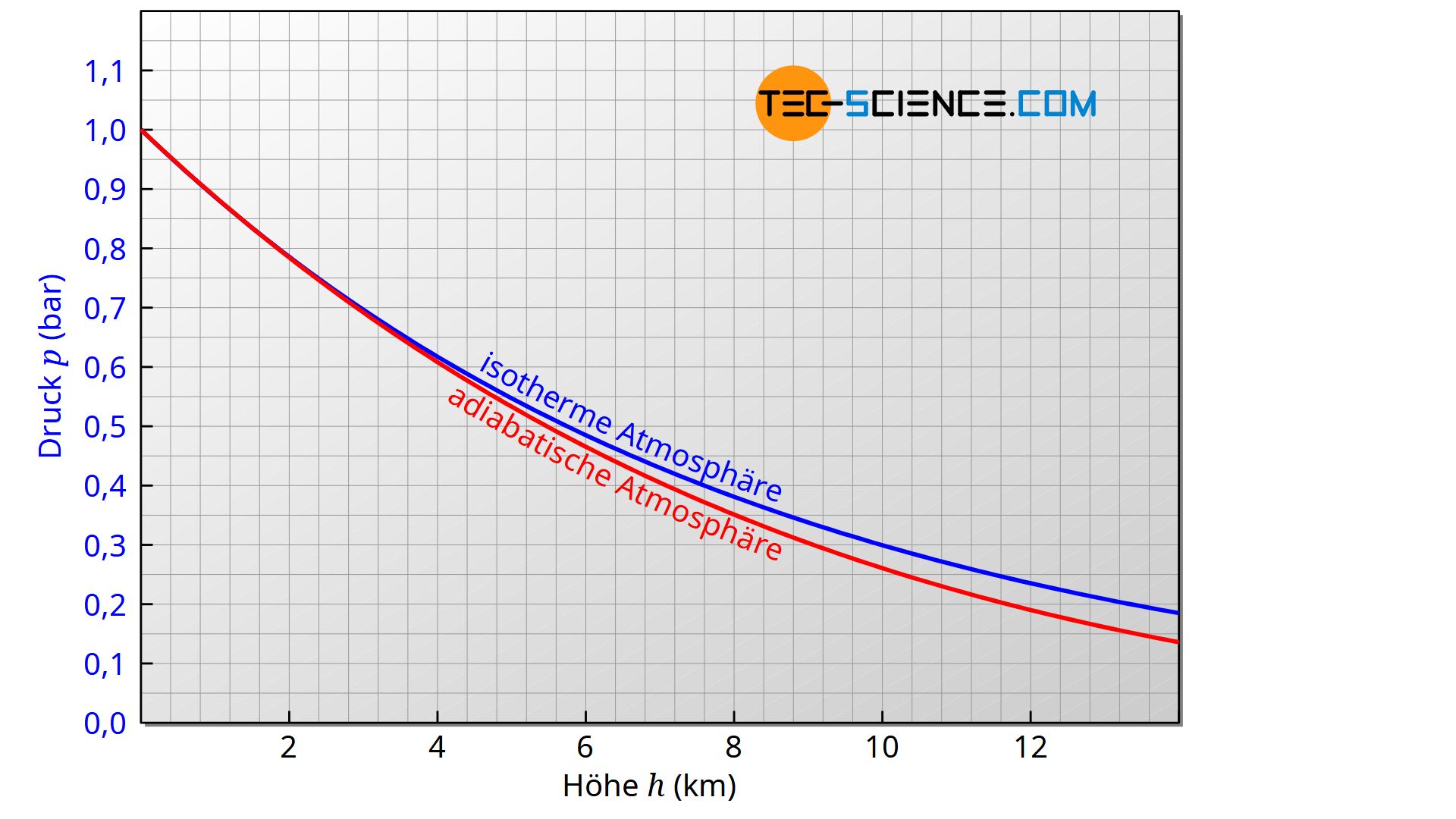
Die untere Abbildung zeigt den Vergleich der klassischen barometrischen Höhenformel einer isothermen Atmosphäre mit der erweiterten Höhenformel einer adiabaten Atmosphäre.

Erweitere barometrische Höhenformel bezüglich der Dichte

Da bei Annahme eines adiabatischen Systems, der Druck in direkter Beziehung zum Volumen und damit zur Dichte steht, kann die erweiterte barometrische Höhenformel auch für die Dichte formuliert werden. Gemäß der Adiabatengleichung stehen Druck und Volumen zweier Zustände wie folgt in Beziehung:

\begin{align}
&p \cdot V^\kappa = p_0 \cdot V_0^\kappa \\[5px]
\end{align}

Dabei beziehen sich Druck p₀ und Volumen V₀ auf ein betrachtetes Luftpaket auf Bezugsniveau und p und V auf die Zustandsgrößen in einer beliebigen Höhe h. Da bei konstanter Masse – die Masse des betrachteten Luftpaketes ändert sich beim Aufstieg nicht – Volumen und Dichte in umgekehrtem Verhältnis zueinander stehen (ϱ=m/V), gilt für den Druck-Dichte-Zusammenhang in einem adiabaten System folgende Beziehung:

\begin{align}
& p \cdot \frac{1}{\rho^\kappa} = p_0 \cdot \frac{1}{\rho_0^\kappa} \\[5px]
& \frac{p}{\rho^\kappa} = \frac{p_0}{\rho_0^\kappa} \\[5px]
& p = p_0 \cdot \left(\frac{\rho}{\rho_0}\right)^\kappa \\[5px]
\end{align}

Dieser Ausdruck für den Druck ist nun in Gleichung (\ref{ext}) einzusetzen und nach der gesuchten Dichte ϱ aufzulösen:

\begin{align}
\require{cancel}
p &= p_0 \cdot \left(1+\frac{\Gamma}{T_0} \cdot h\right)^{ -\frac{g}{R_s \cdot \Gamma }} \\[5px]
\bcancel{p_0} \cdot \left(\frac{\rho}{\rho_0}\right)^\kappa &= \bcancel{p_0} \cdot \left(1+\frac{\Gamma}{T_0} \cdot h\right)^{ -\frac{g}{R_s \cdot \Gamma }} \\[5px]
\frac{\rho}{\rho_0} &= \left(1+\frac{\Gamma}{T_0} \cdot h\right)^{ -\frac{g}{\kappa \cdot R_s \cdot \Gamma }} \\[5px]
\end{align}

\begin{align}
\boxed{\rho(h) = \rho_0 \cdot \left(1+\frac{\Gamma}{T_0} \cdot h\right)^{ -\frac{g}{\kappa \cdot R_s \cdot \Gamma }}} \\[5px]
\end{align}

Formal unterscheidet sich die Formel des Dichteverlaufs von der Formel des Druckverlaufs also nur durch den Exponenten, der an dieser Stelle durch den Adiabatenexponenten geteilt ist.

Die Standardatmosphäre

Die erweiterte barometrische Höhenformel dient zur Beschreibung der sogenannten Standardatmosphäre bis in eine Höhe von rund 85 km. Hierbei wird die Atmosphäre in verschiedene Schichten eingeteilt und innerhalb dieser Schichten ein linearer Temperaturverlauf angenommen.

Meereshöhe in km	Temperaturgradient in K/km	Temperatur in °C
0	-6,5	15,0
11	+0,0	-56,5
20	+1,0	-56,5
32	+2,8	-44,5
47	+0,0	-2,5
51	-2,8	-2,5
71	-2,0	-58,5
85		-84,3

Quelle: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770009539.pdf

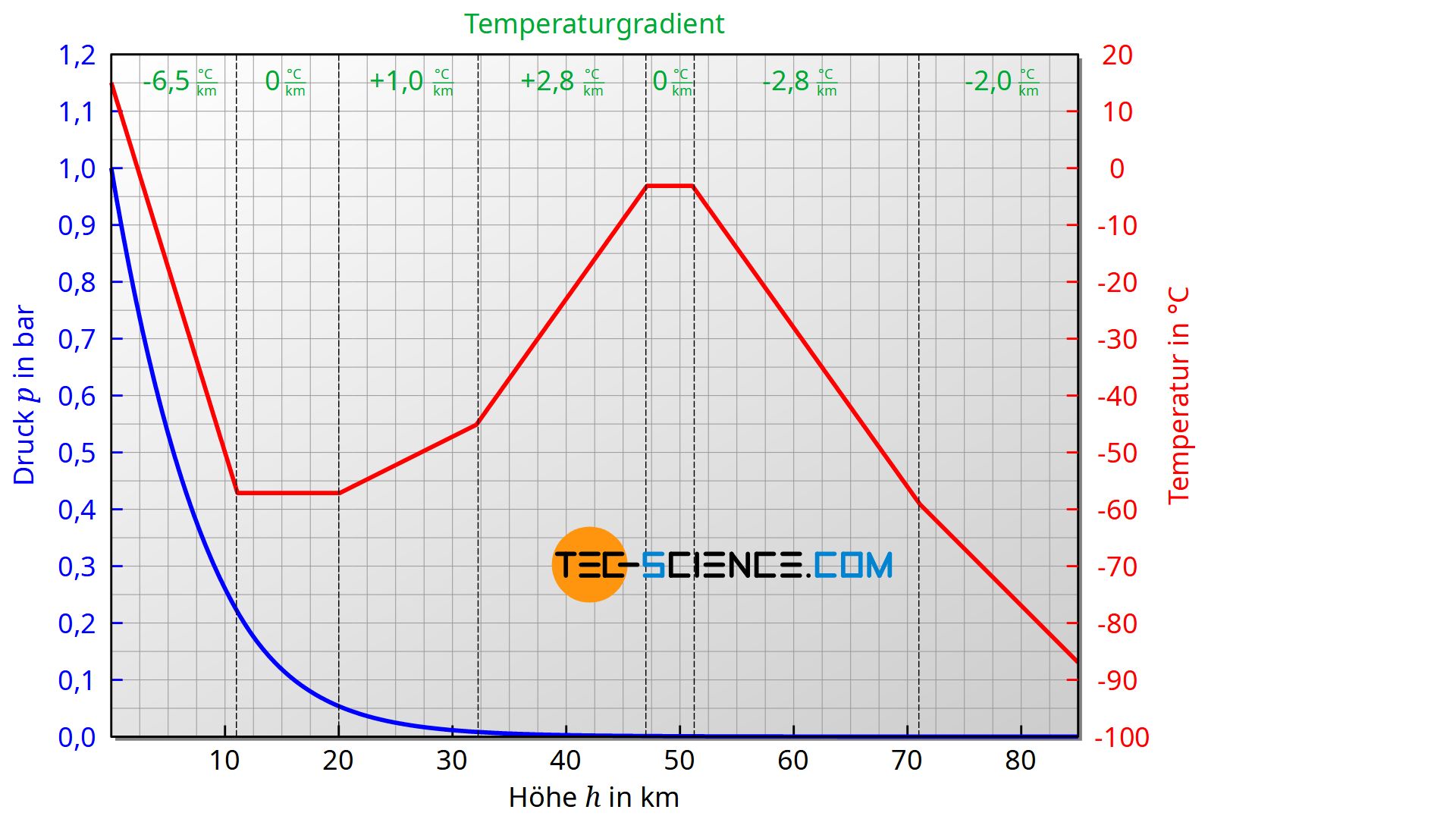
Die Zunahme der Temperatur in der Stratosphäre (ab rund 20 km) ist hauptsächlich der Absorption der UV-Strahlung durch die Ozonschicht geschuldet. Anschließend sinkt die Temperatur wieder bist auf ein Minimum von rund -86 °C bei ca. 90 km. Ab 100 km steigt die Temperatur wieder rasch an und überschreitet bei 300 km sogar 700 °C! Grund hierfür ist die geringe Luftdichte und die damit verbundene große mittlere freie Weglänge. Hierdurch können die Moleküle große Wegstrecken ohne Kollisionen zurücklegen. Dies führt zu relativ hohen Teilchengeschwindigkeiten und somit zu großen Temperaturen. Aufgrund der Tatsache, dass nur wenig Teilchen vorhanden sind, ist die damit verbundene innere Energie des Gases trotzt hoher Temperatur also sehr gering. Deshalb würde man trotzt der hohen Temperaturen dennoch erfrieren, da eben nur sehr geringe Wärmeenergien übertragen werden!

Beachte, dass bei der Beschreibung des Druck in einer isothermen Schicht, die erweiterte barometrische Höhenformel nicht angewendet werden kann. Der Temperaturgradient ist in diesem Fall nämlich Null und steht dabei jedoch im Nenner des Bruchs im Exponenten. Mathematisch gibt es hierfür keine Lösung. In diesem Fall muss entweder ein hinreichend kleiner Temperaturgradient angenommen werden, sodass sich der dabei gemachte Fehler in Grenzen hält, oder es muss die „klassische“ barometrische Höhenformel verwendet werden, die ja explizit für eine isotherme Atmosphäre gilt.