Druck in Flüssigkeiten (hydrostatischer Druck)

Der Druck in einer bestimmten Tiefe einer Flüssigkeit, der aufgrund der Gewichtskraft der darüber liegenden Flüssigkeitssäule zustande kommt, wird als hydrostatischer Druck bezeichnet!

Einleitung

Auf die analoge Weise wie die freien Teilchen in Gasen einen Druck auf Grenzflächen ausüben, so üben auch die Teilchen in Flüssigkeiten einen entsprechenden Druck aus. Im Vergleich zu einem Gas hat eine Flüssigkeit jedoch eine relativ große Dichte. Dies führt in der Praxis zu einer Besonderheit: der Druck in Flüssigkeiten nimmt mit steigender Tiefe mehr und mehr zu. Dies ist der darüber befindlichen Flüssigkeitsschicht geschuldet, die aufgrund ihres Gewichtes eine zusätzliche Kraft auf die betrachtete Flüssigkeitsschicht ausübt. Im Prinzip handelt es sich dabei um den Auflagedruck der darüber befindlichen Flüssigkeitssäule. Da dieser Druck aufgrund der „Schwere“ der Flüssigkeitssäule zustande kommt, bezeichnet man diesen auch als Schweredruck. In der Fachsprache nennt sich dieser Schweredruck hydrostatischer Druck.

Herleitung des hydrostatischen Drucks

Der Auflagedruck

Um das Zustandekommen des hydrostatischen Druck besser zu verstehen, wird zunächst ein zylindrischer Eisklotz mit der Querschnittsfläche A betrachtet. Diese Eissäule hat eine bestimmte Masse m und somit auch eine bestimmte Gewichtskraft F_G=m⋅g. Mit dieser Gewichtskraft drückt die Eissäule auf den darunter befindlichen Boden. Der Auflagedruck, den die Eissäule dabei verursacht, ergibt sich gemäß der Definition des Drucks aus dem Quotienten von (Gewichts-)Kraft und (Auflage-)Fläche:

\begin{align}
\label{p}
&p =\frac{F_G}{A}= \frac{m \cdot g}{A} \\[5px]
\end{align}

Aufgrund der oberen Formel könnte man an dieser Stelle meinen, dass der Auflagedruck von der Querschnittsfläche abhängt ist. Dies ist aber nicht der Fall! Denn wird wird die Querschnittsfläche der Eissäule bei gleichbleibender Höhe verdoppelt, dann verdoppelt sich hierdurch auch die Masse. Der Nenner in Gleichung (\ref{p}) steigt also im selben Maße wie der Zähler. Der Quotient bleibt folglich konstant. Man kann sich an dieser Stelle die dicke Eissäule auch einfach als zwei dünne Eissäulen vorstellen. Jede der Hälften erzeugt dabei denselben Auflagedruck, egal ob diese nun getrennt oder als Ganzes betrachtet werden.

Man kann die Unabhängigkeit des Auflagedrucks von der Auflagefläche auch mathematisch zeigen. Hierzu wird die Masse der Eissäule durch die Dichte ϱ und dessen Volumen V ausgedrückt (m=V⋅ϱ), wobei sich das Volumen wiederum über die Querschnittsfläche A und die Höhe h der Eissäule berechnen lässt (V=A⋅h):

\begin{align}
\label{m}
&m = V \cdot \rho = A \cdot h \cdot \rho \\[5px]
\end{align}

Wird Gleichung (\ref{m}) nun in Gleichung (\ref{p}) eingesetzt, so zeigt sich direkt, dass der Auflagedruck unabhängig von der Größe der Auflagefläche ist und nur von der Dichte des Eises und der Höhe der Eissäule abhängt:

\begin{align}
\require{cancel}
&p =\frac{m \cdot g}{A} = \frac{ \bcancel{A} \cdot h \cdot \rho \cdot g}{\bcancel{A}} \\[5px]
\label{pp}
&\underline{p = h \cdot \rho \cdot g} \\[5px]
\end{align}

Vom Auflagedruck zum hydrostatischen Druck

Die betrachtete Eissäule kann prinzipiell auch in ein zylindrisches Gefäß eingefasst werden. Dies wird nichts am Auflagedruck ändern, mit dem das Eis auf den Boden des Gefäßes drückt. In einem weiteren Schritt kann das Eis auch geschmolzen werden. Dies ändert ebenfalls nichts am Auflagedruck, da beim Schmelzen nicht die Masse des Wassers verändert wird. Die (Gewichts-)Kraft mit der das Wasser auf die Auflagefläche drückt ist also nach wie vor dieselbe und führt gemäß Gleichung (\ref{p}) auch zum selben Auflagedruck (Beachte, dass sich beim Schmelzen zwar die Dichte des Wassers vergrößert, hierdurch sich aber wiederum die Höhe der Wassersäule verringert – auch gemäß Gleichung (\ref{pp}) bleibt der Druck damit konstant).

Der Druck am Boden des Gefäßes kommt also aufgrund der Gewichtskraft der darüber liegenden Wassersäule zustande, egal ob diese gefroren ist oder nicht! Dieser Druck in einer Flüssigkeit, der aufgrund der darüber befindlichen Flüssigkeitssäule verursacht wird, wird auch als hydrostatischer Druck p_h bezeichnet:

\begin{align}
\label{h}
&\boxed{p_h = h \cdot \rho \cdot g} ~~~\text{hydrostatischer Druck} \\[5px]
\end{align}

Der Druck in einer bestimmten Tiefe einer Flüssigkeit, der aufgrund der Gewichtskraft der darüber liegenden Flüssigkeitssäule zustande kommt, wird auch als hydrostatischer Druck bezeichnet!

Wie bereits beim Auflagedruck ausführlich erläutert, so ist auch der hieraus resultierende hydrostatische Druck nicht davon abhängig wie groß die Querschnittsfläche der betrachteten Flüssigkeitssäule ist. Der hydrostatische Druck ist nur abhängig von der Höhe der Säule!

Der hydrostatische Druck ist nur von der Höhe der betrachteten Flüssigkeitssäule abhängig!

Wirkung des hydrostatischen Drucks im Vergleich zum Auflagedruck

Der hydrostatische Druck einer Flüssigkeit unterscheidet sich zwar offensichtlich nicht im Betrag vom Auflagedruck einer gefrorenen Flüssigkeit, aber in der Art der Druckwirkung. Dies zeigt sich, wenn man in Gedanken einen aufgeblasenen Luftballon am Boden des Gefäßes platziert.

Im Falle der gefrorenen Flüssigkeitssäule wirkt der entstehende Auflagedruck salopp formuliert nur nach unten und quetscht den Ballon somit lediglich in der Höhe zusammen. Der hydrostatische Druck der Flüssigkeit wirkt hingegen in jede Richtung gleichermaßen (siehe auch Artikel Druck). Der Ballon wird in diesem Fall von allen Seiten gleichmäßig zusammengequetscht!

Dass der Druck in Flüssigkeiten (oder auch in Gasen) in allen Richtungen gleichermaßen wirkt, zeigt sich auch daran, dass trotz der nach unten wirkenden Gewichtskraft, das im Gefäß befindliche Wasser seitlich durch ein Auslass herausgedrückt wird.

Abhängigkeit des hydrostatischen Drucks von der Tiefe

Ein hydrostatischer Druck wirkt nicht nur am Grund einer Flüssigkeit, sondern in jeder beliebigen Höhe bzw. Tiefe. Man kann sich hierzu wiederum vorstellen als sei die über der betrachteten Tiefe befindliche Flüssigkeitssäule zunächst gefroren. Dies wiederum führt anschaulich zu einem Auflagedruck, mit dem die gefrorene Flüssigkeitssäule auf die darunter befindliche flüssige Flüssigkeitssäule drückt. Nun lässt man in Gedanken wieder die gefrorene Flüssigkeitssäule schmelzen, was am vorhandenen Druck in der betrachteten Tiefe nichts ändert. In Gleichung (\ref{h}) kann also die Höhe h der Flüssigkeitssäule als Tiefe unterhalb der Flüssigkeitsoberfläche interpretiert werden.

Dass der hydrostatische Druck mit zunehmender Tiefe ebenfalls zunimmt, lässt sich auch anschaulich zeigen. Hierzu wird ein Gefäß mit Wasser gefüllt. In verschiedenen Höhen sind Auslässe angebracht, durch die das Wasser ausströmen kann. Man kann nun deutlich sehen, dass das Wasser mit zunehmender Tiefe stärker ausströmt. Dies ist dem zunehmendem Wasserdruck aufgrund des hydrostatischen Drucks geschuldet, der das Wasser mit höherer Geschwindigkeit herauspresst. Werden an den Auslässen Druckmesser angebracht, dann kann der Druck auch quantitativ gemessen werden.

Grundsätzlich ist zu beachten, dass sich der Absolutdruck in einer bestimmten Tiefe nicht nur aus dem hydrostatischen Druck bestimmt. Denn schließlich verursacht nicht nur die Gewichtskraft der Wassersäule einen Druck sondern auch der auf der Wasseroberfläche lastende Luftdruck. Der Gesamtdruck p in einer bestimmten Tiefe ergibt sich somit aus der Summe von Umgebungsdruck p₀ und hydrostatischem Druck p_h. Dies wird häufig auch als Pascalsches Gesetz oder als hydrostatische Grundgleichung bezeichnet.

\begin{align}
&\boxed{p = p_0 + p_h} ~~~\text{Gesamtdruck} \\[5px]
\end{align}

Hydrostatisches Paradoxon

Es wurde bereits erläutert, dass die Querschnittsfläche keinen Einfluss auf den hydrostatischen Druck hat. Dass aber nicht nur die Größe sondern auch die Form des Gefäßes keinen Einfluss hat, soll im Folgenden experimentell und theoretisch gezeigt werden.

Die untere Abbildung zeigt hierzu verschiedene Gefäße mit unterschiedlichen Formen. Die Gefäße sind jeweils mit Wasser gefüllt, wobei die Füllhöhe in allen Fällen identisch ist. Auch die Fläche der Gefäßböden sind in allen Fällen gleich groß. Durch angebrachte Druckmesser können die hydrostatischen Drücke am Boden miteinander verglichen werden. Somit kann der Einfluss der Gefäßform auf den hydrostatischen Druck untersucht werden.

Man könnten nun meinen, dass aufgrund der größeren aufliegenden Wassermasse der hydrostatische Druck im linken Gefäß am größten ist. Paradoxerweise zeigt sich aber, dass die Druckmesser alle denselben Wert anzeigen. Offensichtlich hat die Form der Gefäße keinen Einfluss auf den hydrostatischen Druck. Dies ist auch der Grund, weshalb sich in Gefäßen, die miteinander verbunden sind, überall dieselben Wasserstände einstellen. Aufgrund dieser Tatsache bezeichnet man miteinander verbundenen Gefäße, die über Rohre in Kontakt miteinander sind, auch als kommunizierende Röhren. Mehr Informationen und eine mathematische Herleitung hierzu finden sich im Artikel Anwendungen und Beispiele des hydrostatischen Drucks.

Die Form des Gefäßes hat keinen Einfluss auf den hydrostatischen Druck in der Flüssigkeit!

Dies mag auf den ersten Blick etwas überraschend sein, mit Hilfe des Energieerhaltungssatzes lässt sich dieses Phänomen aber auch anschaulich erklären. Hätte die Form des Gefäßes einen Einfluss auf den hydrostatischen Druck, dann wäre der Energieerhaltungssatz nämlich verletzt, wie folgendes Gedankenexperiment zeigt.

Energetische Betrachtung

In Gedanken stelle man sich hierzu zwei unterschiedlich geformte Gefäße vor. Hätte nun die Form des Gefäßes Einfluss auf den hydrostatischen Druck, dann wäre in einer gemeinsamen Tiefe der Wasserdruck in einem der Gefäße größer als im anderen. Würde man in dieser Tiefe die beiden Gefäße über einen Schlauch miteinander verbinden, dann würde der größere Wasserdruck in einem der Gefäße dazu führen, dass das Wasser im gegenüberliegenden Gefäß nach oben gedrückt wird.

Es käme in der Folge zu einer Höhendifferenz in den Wasserspiegeln. Das nach oben gedrückte Wasser könnte man nun über eine kleine Wasserturbine wieder in das Gefäß mit dem größeren hydrostatischen Druck fließen lassen. Der Kreislauf würde wieder von vorne beginnen. Die Turbine würde also praktisch von selbst laufen und Energie aus dem Nichts erzeugen. Ein solches Perpetuum mobile widerspricht aber dem Energieerhaltungssatz. An dieser Stelle wird also deutlich, dass die Form des Gefäßes aus energetischen Gründen offensichtlich keinen Einfluss auf den hydrostatischen Druck haben kann.

Betrachtung mit einer Kräftebilanz

Dass die Form der Wassersäule keinen Einfluss auf den Wasserdruck hat, kann auch mit Hilfe einer Kräftebilanz gezeigt werden. Das Wasser im trichterförmigen Gefäß hat zwar eine größere Masse und damit ein größeres Gewicht, jedoch wird ein Teil des Gewichtes durch die schrägen Gefäßwände kompensiert. Stellt man sich das Wasser an dieser Stelle wieder gefroren vor, dann wird sofort deutlich, dass die Wände offensichtlich eine Stützkraft ausüben und trotz eventuell offenem Boden das gefrorene Wasser im Gefäß halten.

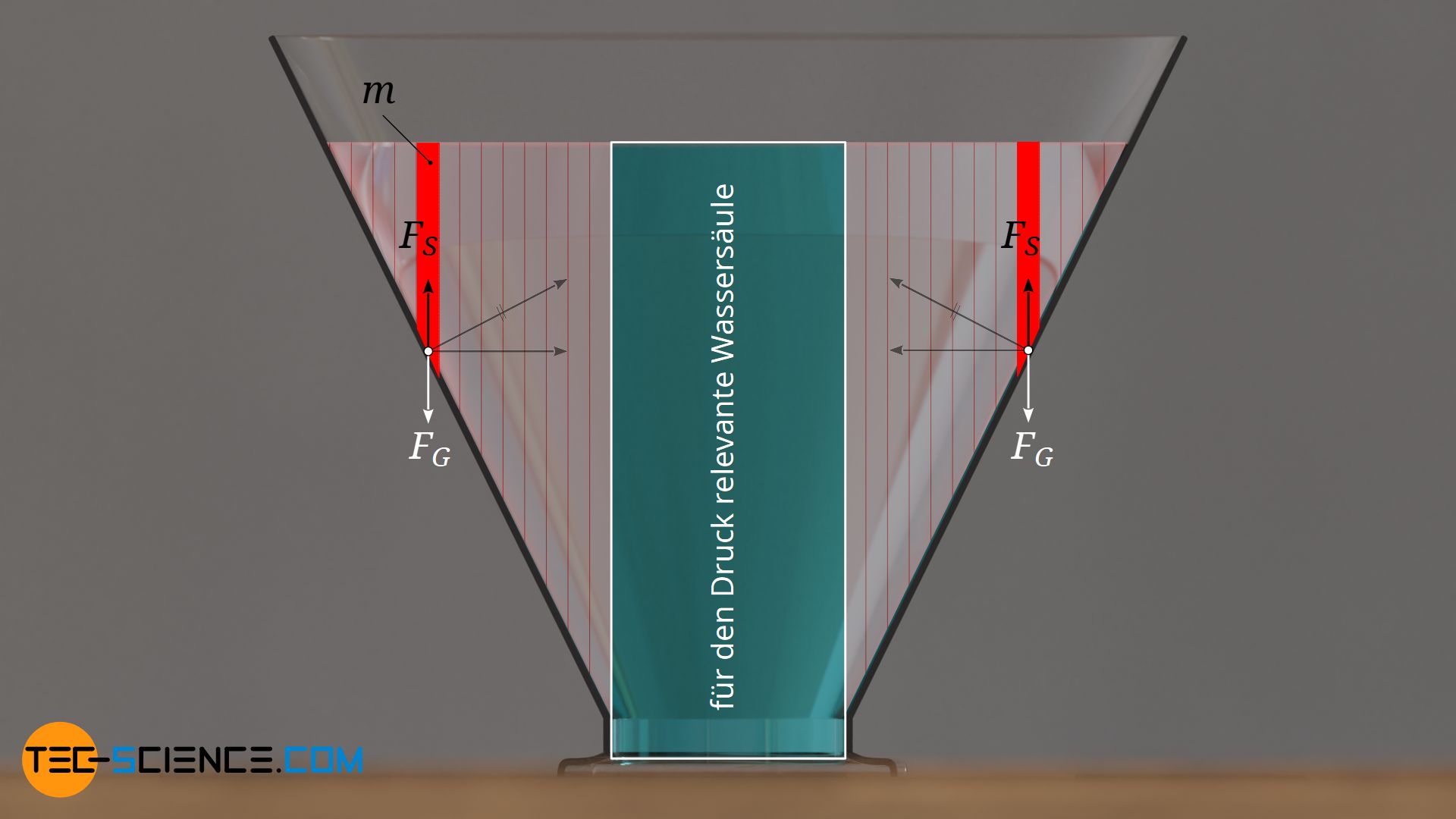
Auch im flüssigen Zustand hält die Gefäßwand die oberhalb liegenden Wassermassen (m) mit einer nach oben gerichteten Stützkraft F_S im Gleichgewicht. Es lastet also gar nicht das gesamte Gewicht des Wassers auf dem Boden, sondern nur die oberhalb des Bodens befindliche Wassersäule (das restliche Gewicht nimmt die Gefäßwand auf). Effektiv betrachtet, erhält man also dieselbe Situation wie im Falle des zylindrischen Gefäßes.

Auch bei dem sich nach oben verjüngenden Gefäß, sind Stützkräfte dafür verantwortlich, dass der Druck am Boden größer ist als man aufgrund der relativ geringen Wassermasse annehmen könnte. Betrachtet man zunächst nur die Wassersäule unterhalb der Gefäßöffnung (schraffierter Bereich im linken Teil des unteren Bildes), dann kann der hydrostatische Druck in einer beliebigen Tiefe wie gewohnt berechnet werden (p_h=ϱ⋅g⋅h). Dieser Druck wirkt in alle Richtungen gleichermaßen. Er drückt in der betrachteten Tiefe somit auch auf die schrägen Gefäßwände und erzeugt damit eine Kraft F_h nach oben.

Dass das Wasser nach oben gedrückt wird, kann man auch anschaulich nachvollziehen. Würde man nämlich Löcher in die Gefäßwand bohren, dann würde das Wasser nach oben gedrückt werden und würde herausströmen. Die Gefäßwände verhindern aber dies durch eine nach unten gerichtete Stützkraft F_S, die offensichtlich genauso groß ist wie die nach oben gerichtete Kraft F_h, die durch den Wasserdruck verursachte wird. Auf das Wasser an den schrägen Gefäßwänden wirkt somit eine Stützkraft nach unten, die betragsmäßig genauso groß ist wie die Gewichtskraft einer darüber befindlichen Wassersäule. Effektiv betrachtet, hat man es also wieder mit einer zylindrischen Wassersäule zu tun, dessen Durchmesser dem Durchmesser des Bodens entspricht. Man erhält schließlich dieselbe Situation wie im Falle des zylindrischen Gefäßes.

Einfluss von eintauchenden Gegenständen auf den hydrostatischen Druck

Nicht nur die Gefäßform, sondern auch bspw. das Auflegen eines schwimmenden Körpers auf die Wasseroberfläche hat ebenfalls keinen Einfluss auf die Gesetzmäßigkeit zur Berechnung des hydrostatischen Drucks. Die untere Abbildung zeigt hierzu ein Gefäß mit Wasser, in das eine schwimmende Kugel eingelegt wird.

Tatsächlich wird der hydrostatische Druck in einer bestimmten Tiefe durch die aufgelegte Kugel steigen, denn schließlich lastet auf die betrachtete Grenzfläche nun nicht mehr nur die Gewichtskraft des darüber befindlichen Wassers, sondern zusätzlich noch die Gewichtskraft der Kugel. Der vergrößerte hydrostatische Druck lässt sich aber auch rein mit dem Ansteigen des Wasserspiegels erklären, der mit dem Auflegen der schwimmenden Kugel verbunden ist.

An der Tatsache, dass der hydrostatische Druck nach wie vor nur von der Wassertiefe abhängig ist (welche durch Auflegen der Kugel nun größer ist), ändert sich also nichts! Diese Betrachtungsweise führt schließlich zum sogenannten Archimedischen Prinzip, das besagt, dass die Auftriebskraft eines schwimmenden Körpers genauso groß ist wie die Gewichtskraft der verdrängten Flüssigkeit. Mehr Informationen hierzu im Artikel Auftrieb.

Ausblick

Der hydrostatische Druck hat im Alltag und in der Technik eine große Bedeutung. Im Artikel Anwendungen und Beispiele des hydrostatischen Drucks finden sich hierzu nähere Informationen.