Berechnung der Nusselt-Zahlen für erzwungene Strömungen über Platten und in Rohren

In diesem Artikel finden Sie Formeln zur Berechnung der lokalen und mittleren Nusselt-Zahlen für erzwungene Strömungen über Platten und in Rohren mit kreisförmigem Querschnitt.

Nusselt-Zahl

Die Definition und die Bedeutung der Nusselt-Zahl als Ähnlichkeitskenngröße wurde im entsprechenden Artikel bereits ausführlich erläutert. Mit Hilfe dieser Kenngröße kann in Abhängigkeit der charakteristischen Länge eines um- oder durchströmten Körpers, der Wärmeübergangskoeffizient berechnet werden. Damit lässt sich anhand der Temperaturdifferenz zwischen Wand und Fluid schließlich die Wärmestromdichte ermitteln. Dies entspricht dem Wärmestrom pro Flächeneinheit, der von der Wand auf das Fluid (bei beheizter Wand) oder vom Fluid auf die Wand (bei beheiztem Fluid) übertragen wird.

\begin{align}
\label{qq}
&\boxed{\dot q = \alpha \cdot \Delta T} \\[5px]
&\boxed{\alpha = Nu \cdot \frac{\lambda_F}{L}} \\[5px]
\end{align}

\begin{align}
\notag&\dot q ~&& \text{Wärmestromdichte} \\[5px]
\notag&\alpha ~&& \text{Wärmeübergangskoeffizient} \\[5px]
\notag&\Delta T~&& \text{Temperaturdifferenz zwischen Wand und Fluid} \\[5px]
\notag&Nu~&& \text{Nusselt-Zahl} \\[5px]
\notag&\lambda_F~&& \text{Wärmeleitfähigkeit des Fluids} \\[5px]
\notag&L~&& \text{charakteristische Länge des Systems} \\[5px]
\end{align}

Die charakteristische Länge entspricht bei einer Rohrströmung dem Innendurchmesser des Rohres und bei einer umströmten Platte der Plattenlänge in Strömungsrichtung. Die Fluidtemperatur zur Berechnung der Temperaturdifferenz bezieht sich bei umströmten Objekten auf die Temperatur in der freien Anströmung (T_F,∞). Bei Rohrströmungen legt man für den lokalen Wärmeübergang die adiabate Mischtemperatur zugrunde (T_F), d.h. jene Temperatur die man erhalten würde, wenn man das Fluid an der betrachteten Stelle ideal mischen würde.

Funktionale Abhängigkeit der Nusselt-Zahl

Grundsätzlich ist die Nusselt-Zahl keine Stoffkonstante, sondern wird maßgeblich durch die Eigenschaft der Strömung im Hinblick auf Geschwindigkeit und Wärmeleitung bestimmt. Die Strömungsgeschwindigkeit wird dabei in Form der dimensionslosen Reynoldszahl Re beschrieben. Ebenfalls erfolgt die Berücksichtigung der Wärmeleitung mit Hilfe einer dimensionslosen Kenngröße, der sogenannten Prandtl-Zahl Pr. Diese beschreibt den Impulstransport zwischen den einzelnen strömenden Fluidschichten im Verhältnis zum Energietransport durch Wärmeleitung. Für die Nusselt-Zahl gilt im Allgemeinen also folgende funktionale Abhängigkeit:

\begin{align}
&\overline{Nu}= \overline{Nu} (Re, Pr) \\[5px]
\end{align}

Beachte, dass bei Zugrundelegung der Reynoldszahl die Strömungsart eine entscheidende Rolle spielt, d.h. ob die Strömung laminar oder turbulent ist. Bei turbulenten Strömungen nehmen die Nusselt-Zahlen im Allgemeinen sehr große Werte an, da die hierdurch hervorgerufene Durchmischung zu einem erhöhten Transport von Impuls und Energie quer zur Strömungsrichtung führt. Dies resultiert folglich in einem hohen Wärmestrom.

Im Folgenden soll für eine längsangeströmte Platte und für eine Rohrströmung mir kreisförmigem Querschnitt die Berechnung der Nusselt-Zahlen gezeigt werden. Diese Berechnungen beziehen sich im Wesentlichen auf den VDI Wärmeatlas (7. Auflage, 1994). Die Formeln gelten ausschließlich für erzwungene Strömungen durch Pumpen oder Gebläse und nicht für die freie Konvektion.

Berechnung der Nusselt-Zahl für längsangeströmte ebene Platten

Laminare Strömung

Für Reynoldszahlen kleiner 10.000 und Prandtl-Zahlen zwischen 0,6 und 2000 kann die mittlere Nusselt-Zahl bei einer laminaren Umströmung einer ebenen Platte, die isotherm beheizt oder gekühlt wird, mit folgender Formel berechnet werden:

\begin{align}
\label{nul}
&\boxed{\overline{Nu}_\text{lam}= 0,664 \cdot \sqrt{Re} \cdot \sqrt[3]{Pr}} \\[5px]
& Re<10^5 ~~\text{und}~~0,6<Pr<2000 \\[5px]
\end{align}

Die Stoffwerte zur Berechnung der Reynolds- und Prandtl-Zahl beziehen sich auf die mittlere Temperatur des strömenden Fluids. Bezeichnet T₁ die Temperatur des Fluids am Anfang der Platte und T₂ die Temperatur am Ende, dann gilt für die mittlere Temperatur T_m=(T₁+T₂)/2.

Damit die Platte laminar umströmt wird, sollte die Umströmkante möglichst stromlinienförmig ausgeführt sein. Bei einer scharfen Kante kommt es sonst zu Verwirbelungen und somit zu Turbulenzen in der Grenzschicht.

Turbulente Strömung

Handelt es sich bei der Umströmung der isotherm beheizt oder gekühlten Platte um eine turbulente Strömung in der Grenzschicht, dann kann bei konstanter Wandtemperatur nachfolgende Formel zur Berechnung der mittleren Nusselt-Zahl angewendet werden. Diese Formel beruht auf den Untersuchungen von Petukov (High Temperature I, 1963) und Schlichting (Grenzschicht-Theorie, 1958).

\begin{align}
\label{nut}
&\boxed{\overline{Nu}_\text{tur}= \frac{0,037 \cdot Re^{0,8}\cdot Pr}{1+2,443 \cdot Re^{-0,1} \left(Pr^{\frac{2}{3}}-1\right)} } \\[5px]
&5 \cdot 10^5 <Re<10^7 ~~\text{und}~~0,6<Pr<2000\\[5px]
\end{align}

Die Reynolds-Zahlen liegen bei turbulenter Strömung definitionsgemäß oberhalb der kritischen Reynolds-Zahlen. Für die Gültigkeit der oberen Formel sollten die Reynolds-Zahlen deshalb im Bereich zwischen 5⋅10⁵ und 10⁷ liegen. Für die Prandtl-Zahlen gilt ein Bereich zwischen 0,6 und 2000. Die Stoffwerte zur Bestimmung dieser dimensionslosen Größen beziehen sich wiederum auf die mittlere Fluidtemperatur.

Laminare und turbulente Strömung

In der Praxis zeigt sich selbst bei moderaten Reynolds-Zahlen meist keine vollständig laminare Umströmung. Ursächlich ist die nicht perfekt stromlinienförmig ausgeführte Kante der Platte. Zudem wird die Platte in der Praxis nie exakt parallel angeströmt, d.h. es ist bereits ein geringer Turbulenzgrad in der Anströmung enthalten. Nach einer laminaren Anlaufstrecke geht die Strömung innerhalb eines Übergangsgebiets deshalb in eine turbulente Strömung über. Dabei bildet sich eine laminare Unterschicht über die gesamte Platte hinweg.

Für die kritische Reynolds-Zahl Re_krit, ab der mit einem Übergang vom laminaren zum turbulenten Bereich zu rechnen ist, gilt:

\begin{align}
&\boxed{Re_\text{krit}= \frac{v_\infty \cdot x_\text{krit}}{\nu}=5 \cdot 10^5} \\[5px]
\end{align}

Darin bezeichnet v_∞ ist die Geschwindigkeit der freien Anströmung.

Für Reynolds-Zahlen zwischen 10 und 10⁷ bildet man für Strömungen mit laminar-turbulentem Übergang die mittlere Nusselt-Zahl wie folgt:

\begin{align}
\label{nuu}
&\boxed{\overline{Nu}= \sqrt{\overline{Nu}_\text{lam}^2 + \overline{Nu}_\text{tur}^2}} \\[5px]
&10 < Re < 10^7 ~~\text{und}~~0,6<Pr<2000\\[5px]
\end{align}

Die Nusselt-Zahlen Nu_lam und Nu_tur sind mit den Formeln (\ref{nul}) und (\ref{nut}) zu ermitteln.

Berücksichtigung der Wärmestromrichtung und der Temperaturabhängigkeit der Stoffwerte

Bei Berechnung der Nusselt-Zahlen muss grundsätzlich berücksichtigt werden, ob Wärme vom Fluid auf die Platte übergeht oder umgekehrt, die Platte Wärme auf das Fluid überträgt. Je nachdem hat man nämlich trotz identischer Fluidtemperatur (die ja auf die freie Anströmung bezogen wird) eine andere Temperaturverteilung im Fluid. Dies hat Auswirkungen auf die Stoffwerte des Fluids.

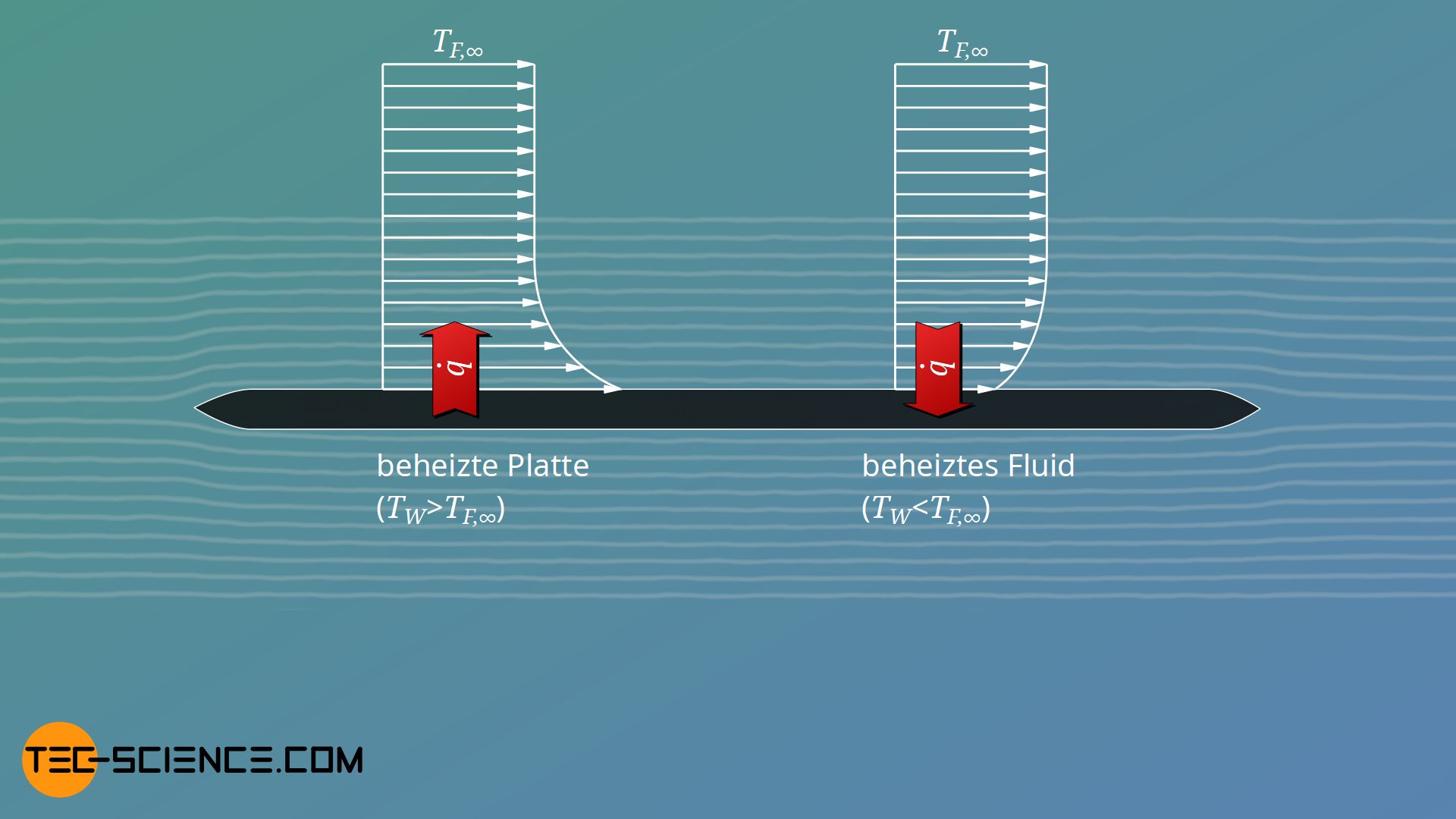
So nimmt bspw. bei Flüssigkeiten die Viskosität mit steigender Temperatur ab. Dies beeinflusst die Geschwindigkeitsgrenzschicht und somit den Wärmeübergang. Für Flüssigkeiten kann dies durch nachfolgend angegebenen Faktor berücksichtigt werden, der im Anschluss auf die berechneten Nusselt-Zahlen anzuwenden ist:

\begin{align}
&\boxed{\overline{Nu}^*= \overline{Nu} \cdot \left(\frac{Pr}{Pr_W}\right)^{0,25} } ~~~~~\text{gilt für Flüssigkeiten}\\[5px]
\end{align}

Nicht nur die Wärmestromrichtung, sondern generell die Abhängigkeit der Stoffwerte von der Temperatur wird auf diese Weise berücksichtigt. Dabei bezieht sich die Prandtl-Zahl Pr zunächst wieder auf mittlere Flüssigkeitstemperatur, während sich die Prandtl-Zahl Pr_W diesmal auf die Stoffwerte bei Wandtemperatur bezieht. Für Gase wird der Faktor zur Berücksichtigung der Temperaturabhängigkeit meist direkt über das Verhältnis der Temperaturen zwischen Fluid und Wand gebildet, da bei Gasen die Prandtl-Zahl nicht stark von der Temperatur beeinflusst wird:

\begin{align}
&\boxed{\overline{Nu}^*= \overline{Nu} \cdot \left(\frac{T_F}{T_W}\right)^{0,12} } ~~~~~\text{gilt für Gase}\\[5px]
\end{align}

Berechnung der Nusselt-Zahl für erzwungene Rohrströmungen

Definition des mittleren Wärmeübergangskoeffizienten

Im Folgenden betrachten wir das Strömen eines Fluids durch ein beheiztes oder gekühltes Rohr mit der konstanten Wandtemperatur T_W. Die Temperatur des Fluids beim Eintritt in das Rohr betrage T₁ und beim Austritt T₂. Dabei hat das Fluid beim Austritt allerdings keine einheitliche Temperatur über den Rohrquerschnitt. Die Austrittstemperatur T₂ bezieht sich deshalb auf die adiabate Mischtemperatur.

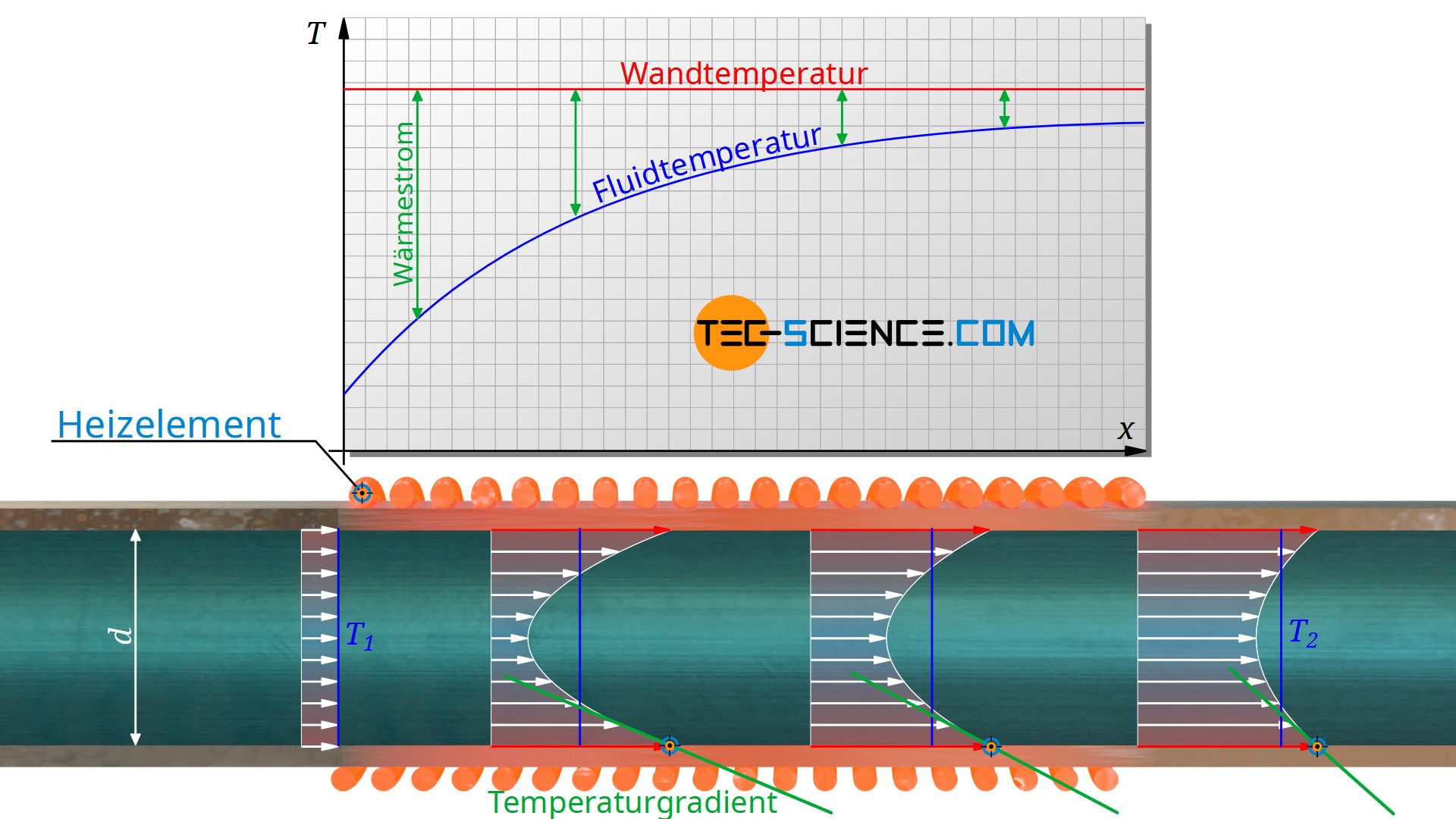
Zur Berechnung des konvektiven Wärmeübergangs gemäß Gleichung (\ref{qq}) ist die Temperaturdifferenz zwischen Wand und Fluid von Bedeutung. Die Fluidtemperatur ändert sich allerdings über die Rohrlänge hinweg. Bei einem isotherm beheizten Rohr nimmt die Temperatur des Fluids beim Durchströmen permanent zu. Zu Beginn wird aufgrund der relativ großen Temperaturdifferenz zwischen Wand und Fluid mehr Wärme übertragen als gegen Ende des Rohres. Man definiert als Temperaturdifferenz deshalb eine logarithmische Temperaturdifferenz ΔT_ln:

\begin{align}
&\boxed{\Delta T_\text{ln}:=\frac{\Delta T_\text{ein}-\Delta T_\text{aus}}{\ln\left(\frac{\Delta T_\text{ein}}{\Delta T_\text{aus}} \right)}} ~~~~~\text{logarithmische Temperaturdifferenz} \\[5px]
&\Delta T_\text{ln}=\frac{(T_\text{W}-T_1)-(T_\text{W}-T_2)}{\ln\left(\frac{T_\text{W}-T_1}{T_\text{W}-T_2} \right)} \\[5px]
\end{align}

Mit α als mittlerer Wärmeübergangskoeffizient gilt für die Wärmestromdichte des Rohres somit:

\begin{align}
&\boxed{\overline{\dot q} = \overline{\alpha} \cdot \Delta T_\text{ln} } \\[5px]
\end{align}

Der mittlere Wärmeübergangskoeffizient bestimmt sich über die mittlere Nusselt-Zahl (mit dem Rohrinnendurchmesser d als charakteristische Länge):

\begin{align}
&\boxed{\overline{\alpha} =\overline{Nu} \cdot \frac{\lambda_F}{d}} \\[5px]
\end{align}

Definition der Profilfaktoren

Für Rohrströmungen hängt das Temperaturprofils und damit die Nusselt-Zahl nicht nur von der Reynolds-Zahl und der Prandtl-Zahl ab. Es muss auch berücksichtigt werden welchen Innendurchmesser d das Rohr im Verhältnis zu seiner Länge l hat. Die mittlere Nusselt-Zahl Nu hängt bei Rohrströmungen deshalb im Allgemeinen von folgendem mittleren Profilfaktor β ab:

\begin{align}
&\boxed{\overline{\beta}:=Re \cdot Pr \cdot \frac{d}{l}} ~~~~~\text{mittlerer Profilfaktor} \\[5px]
&\boxed{\overline{Nu}=\overline{Nu}(\overline{\beta})} \\[5px]
\end{align}

Die Länge l bezieht sich nicht zwangsweise auf das gesamte Rohr, sondern grundsätzlich nur auf jenen Abschnitt innerhalb dessen ein Wärmeaustausch zwischen Rohr und Fluid stattfindet. Der Einfachheit halber wird aber meist von der Rohrlänge gesprochen.

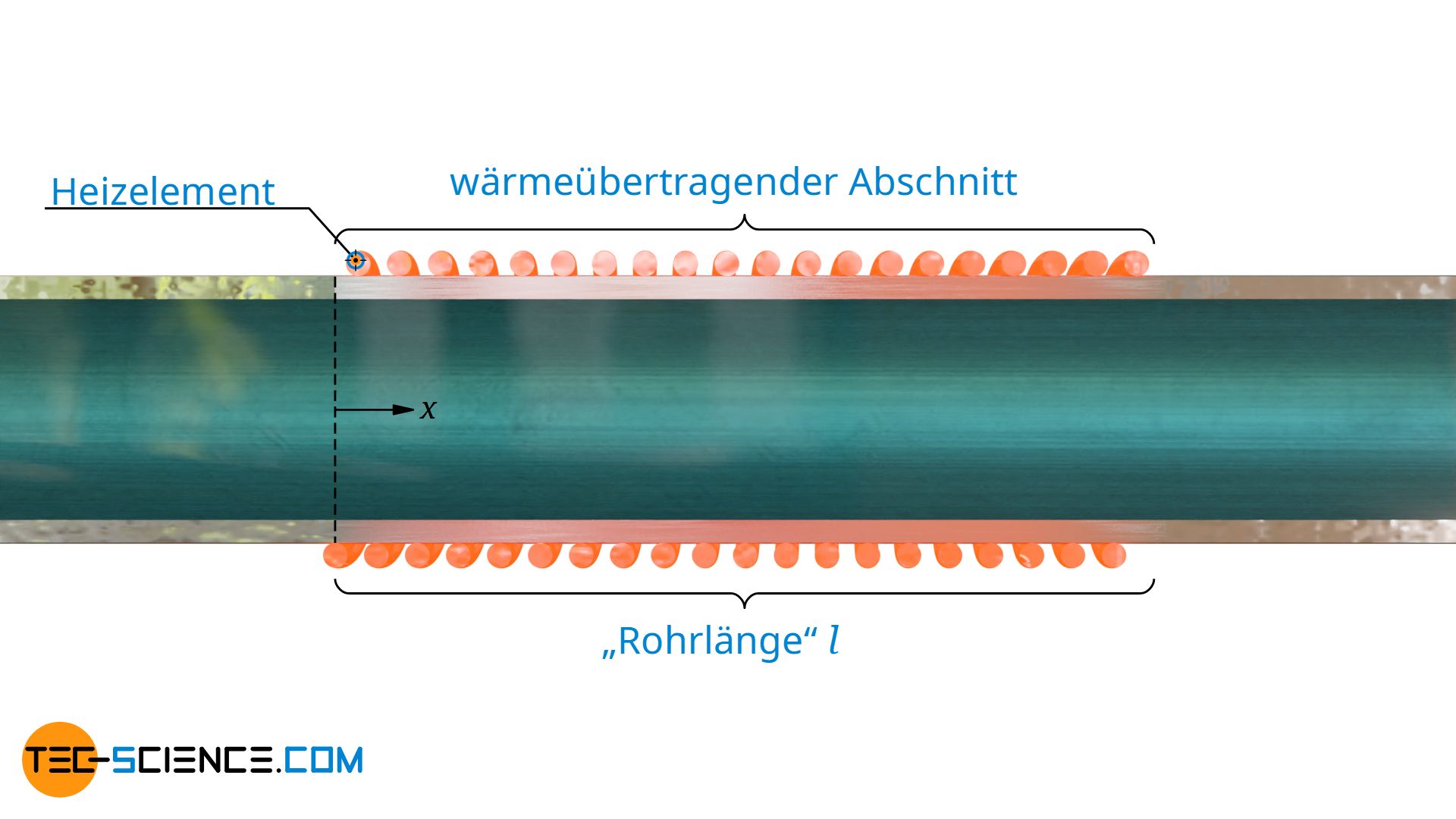
Für die lokale Nusselt-Zahl Nu ist anstelle der Rohrlänge l lediglich die Rohrlänge bis zur betrachteten Position x zu verwenden. Man spricht dann vom lokalen Profilfaktor β. Die Position x bezieht sich dabei wieder auf den Beginn des Wärmeaustauschs im Rohr.

\begin{align}
&\boxed{\beta:=Re \cdot Pr \cdot \frac{d}{x}} ~~~~~\text{lokaler Profilfaktor} \\[5px]
&\boxed{Nu=Nu(\beta)} \\[5px]
\end{align}

Die Stoffwerte zur Berechnung der Reynolds- und Prandtl-Zahl beziehen sich wieder auf die mittlere Temperatur des strömenden Fluids. Bezeichnet T₁ die Temperatur des einströmenden Fluids in das Rohrs und T₂ die Temperatur des Fluids beim Ausströmen (Mischtemperatur), dann gilt für die mittlere Temperatur T_m = (T₁+T₂)/2.

Anmerkung: Das Produkt von Reynolds-Zahl und Prandtl-Zahl im Profilfaktor wird auch als Péclet-Zahl Pe bezeichnet. Der Profilfaktor kann daher auch über die Péclet-Zahl definiert werden:

\begin{align}
&\boxed{Pe:=Re \cdot Pr}= \frac{v \cdot L}{a}&&~~~~~\text{Péclet-Zahl} \\[5px]
&\beta=Pe \cdot \frac{d}{l} &&~~~~~\text{mittlerer Profilfaktor} \\[5px]
&\beta=Pe \cdot \frac{d}{x} &&~~~~~\text{lokaler Profilfaktor} \\[5px]
\end{align}

Beachte, dass die Péclet-Zahl nur durch die mittlere Strömungsgeschwindigkeit v, der Temperaturleitfähigkeit a des Fluids und der charakteristischen Länge L des Systems bestimmt ist. Sie ist nicht von der Viskosität des Fluids abhängig! Insofern spielt für die nachfolgend erläuterten Wärmeübergänge in Rohren die Viskosität des Fluids auch keine Rolle.

Grenzwerte der Nusselt-Zahlen

Im Artikel zur Nusselt-Zahl wurde gezeigt, dass je nach Randbedingung unter der Voraussetzung einer hydrodynamisch und thermisch vollständig ausgebildeten Rohrströmung, die Nusselt-Zahlen folgende Grenzwerte anstreben:

\begin{align}
\label{366}
&\boxed{Nu_{\infty}= 3,660} &&~~~\text{bei konstanter Wandtemperatur}\\[5px]
\label{4364}
&\boxed{Nu_{\infty}= 4,364} &&~~~\text{bei konstanter Wärmestromdichte an der Wand}\\[5px]
\end{align}

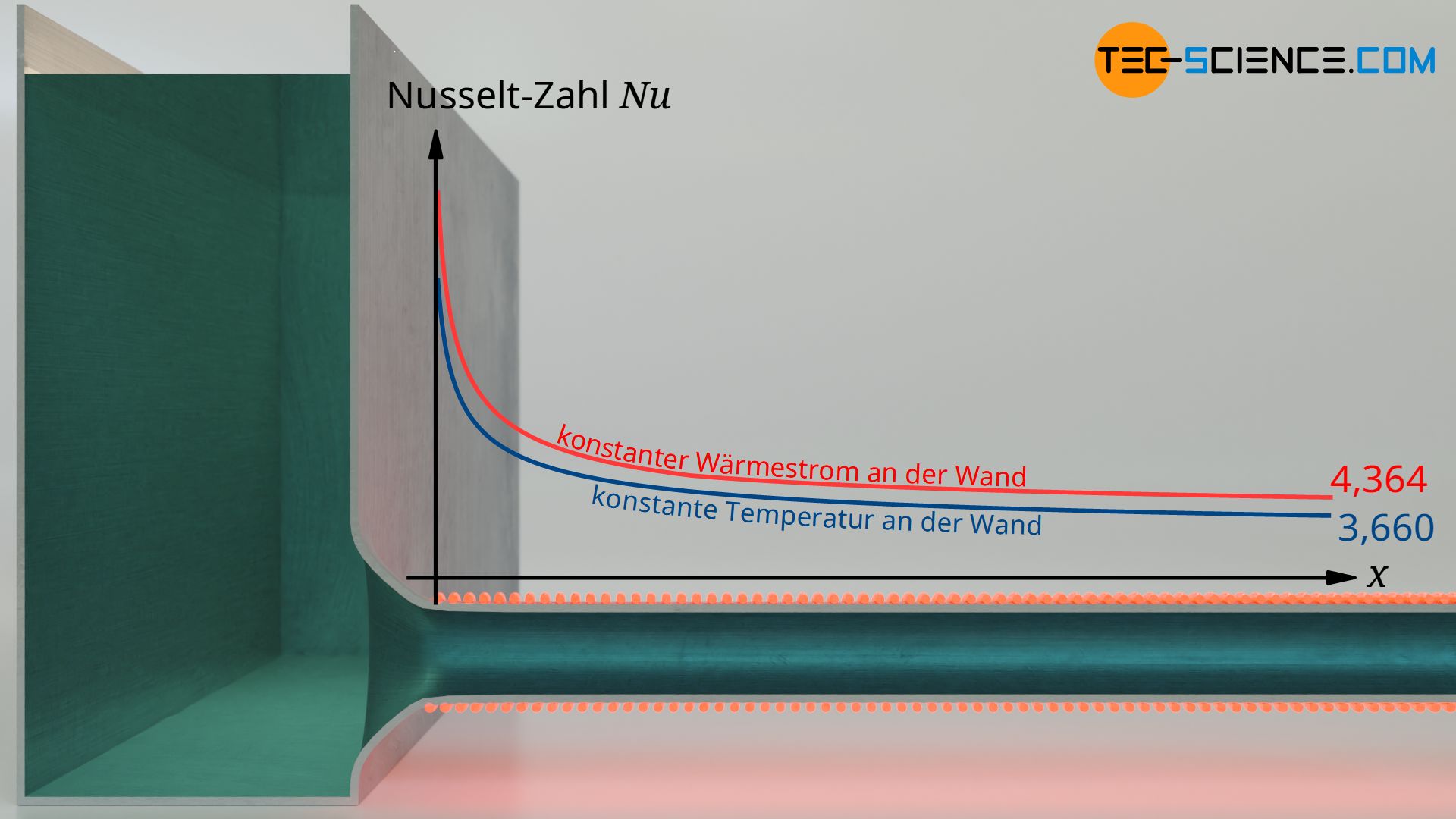
Dies ist insofern bemerkenswert als dass offensichtlich weder die Reynolds-Zahl noch die Prandtl-Zahl diese Grenzwerte beeinflusst. Diese Grenzwerte gelten allerdings nur für vollständig ausgebildete Strömungen, die in der Praxis bei endlichen Rohrlängen im Allgemeinen nicht gegeben sind.

Laminare Rohrströmung bei konstanter Wandtemperatur

Hydrodynamisch ausgebildete Strömung (lange Rohre)

Die mittlere Nusselt-Zahl Nu ergibt sich bei hydrodynamisch ausgebildeter Strömung (ausgebildetes Geschwindigkeitsprofil) in Abhängigkeit des mittleren Profilfaktors β wie folgt:

\begin{align}
\label{nu_lg}
&\boxed{\overline{Nu}= \sqrt[3]{49,371 + \left(1,615 \cdot \sqrt[3]{\overline{\beta}}-0,7 \right)^3} } \\[5px]
&\overline{\beta}=Re \cdot Pr \cdot \frac{d}{l}\\[5px]
\end{align}

Eine ausgebildete Rohrströmung liegt bspw. vor, wenn das Fluid bereits durch eine ausreichend lange Vorlaufstrecke geströmt ist, bevor es in den eigentliche wärmeübertragende Rohrabschnitt der Länge l gelangt.

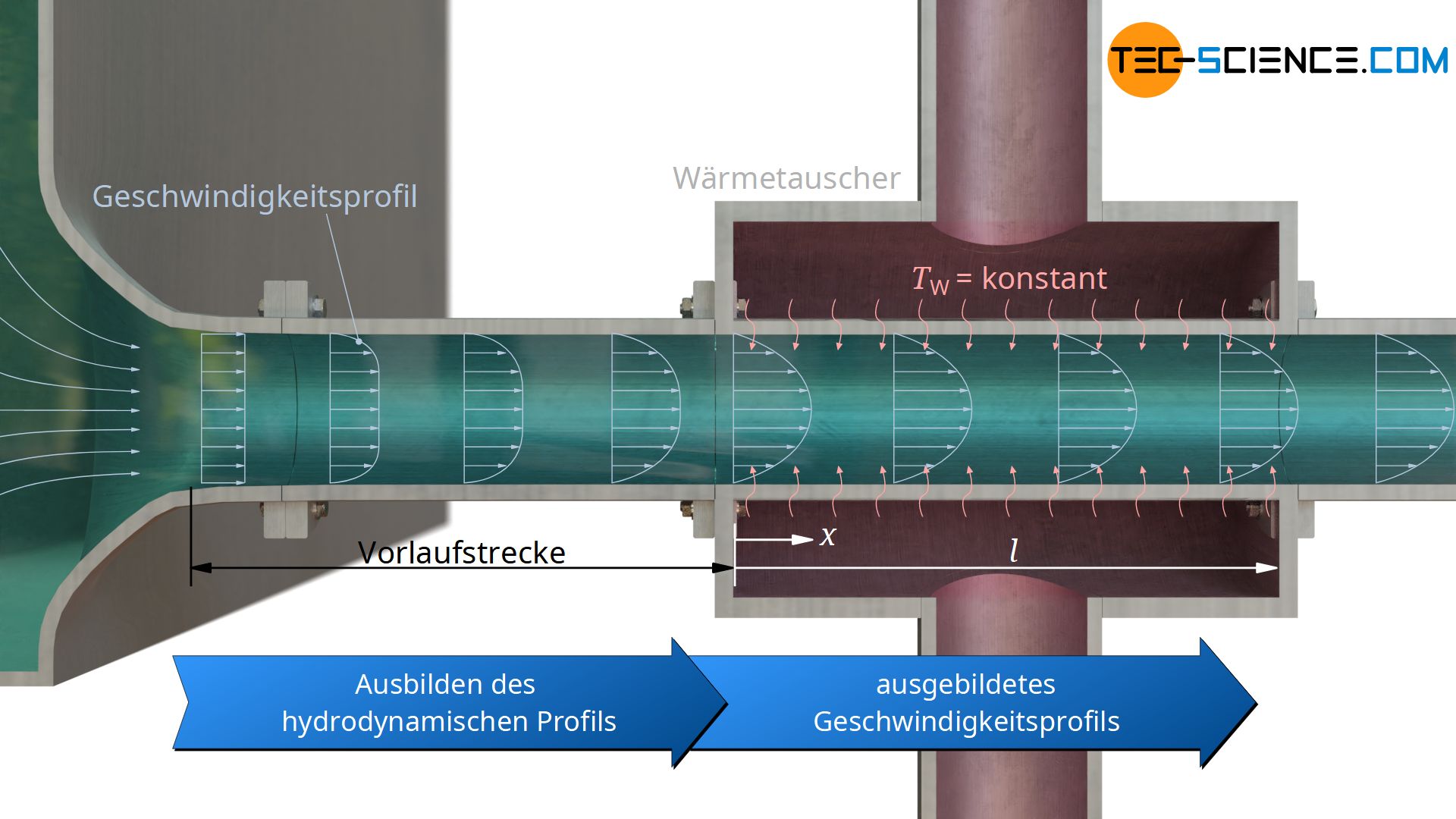
Die lokale Nusselt-Zahl Nu an einer bestimmten Stelle x, gemessen vom Beginn des Wärmeübertragung, kann bei hydrodynamisch ausgebildeter Strömung mit Hilfe des lokalen Profilfaktors β ermittelt werden:

\begin{align}
\label{nu_ll}
&\boxed{Nu= \sqrt[3]{49,371 + \left(1,077 \cdot \sqrt[3]{\beta}-0,7 \right)^3} } \\[5px]
&\beta=Re \cdot Pr \cdot \frac{d}{x} \\[5px]
\end{align}

Beachte, dass die Profilfaktoren in den oberen Formeln für sehr lange Rohre gegen Null gehen. Die Nusselt-Zahlen nähert sich in diesen Fällen immer mehr der ortsunabhängigen Nusselt-Zahl von 3,660 an [siehe Gleichung (\ref{366})]:

\begin{align}
& \lim \limits_{l \to \infty}\beta \rightarrow 0 ~~~\Rightarrow~~~ Nu\rightarrow 3,660 \\[5px]
\end{align}

Berücksichtigung des hydrodynamischen Anlaufs (kurze Rohre)

Im Folgenden betrachten wir ein Fluid, das in eine Rohrleitung einströmt und unmittelbar am Rohranfang beheizt oder gekühlt wird. Man kann sich hierzu einen großen Tank vorstellen, aus dem über eine angebrachte Rohrleitung Flüssigkeit ausströmt. Die Rohrleitung wird unmittelbar beheizt. In diesem Fall wird sich das hydrodynamische Strömungsprofil erst nach eine gewissen Anlaufstrecke vollständig ausgebildet haben.

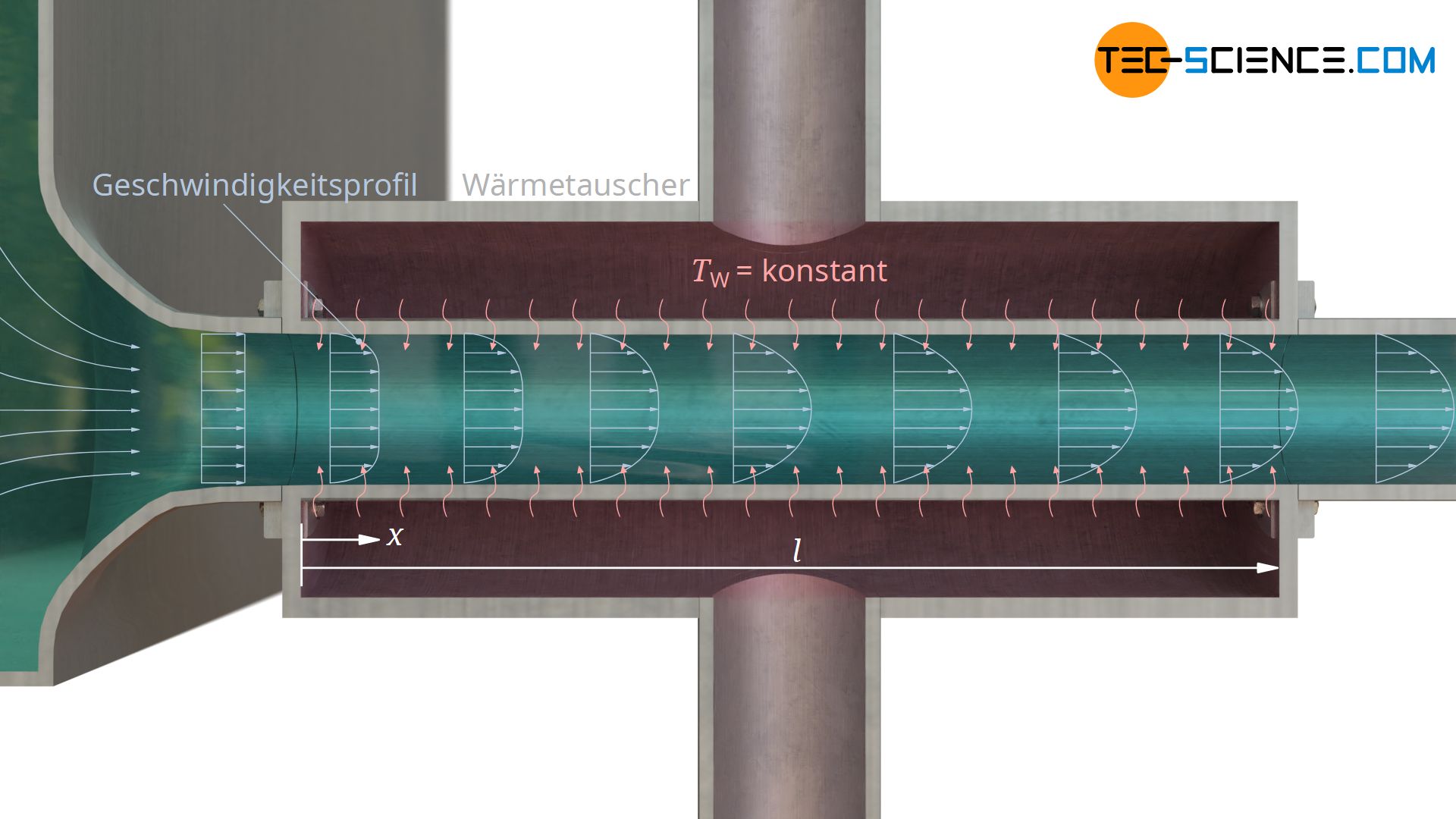
Ursache hierfür ist die Viskosität des Fluid und die damit verbundene Reibungskraft. Diese führt an der Wand zu einer Abbremsung des Fluids und in der Mitte zu einer Beschleunigung aufgrund der Massenerhaltung. Für ein newtonsches Fluid mit konstanter Viskosität würde sich über die Anlaufstrecke hinweg ein parabolisches Geschwindigkeitsprofil ausbilden (Hagen-Poiseuille Strömung). Davon kann in diesem Fall aber nicht mehr ausgegangen werden, da das Fluid bei einer Beheizung oder Kühlung keine konstante Temperatur über den Querschnitt hinweg aufweist. Somit ist auch die Viskosität nicht mehr konstant.

Unabhängig davon welches Geschwindigkeitsprofil sich nun genau einstellt, ist im Anlauf ein anderes Geschwindigkeitsprofil vorhanden als bei ausgebildeter Strömung. Das Geschwindigkeitsprofil beeinflusst aber das Temperaturprofil und somit auch den gesamten Wärmeübergang. Aus diesem Grund gelten unter Berücksichtigung des hydrodynamischen Anlaufs andere Nusselt-Zahlen als bei ausgebildeter hydrodynamischer Strömung.

Insbesondere für kurze Rohre, bei denen der Anlauf einen relativ großen Anteil an der gesamten Rohrlänge hat, ist dies entscheidend. Es ist davon auszugehen, dass aufgrund der höheren Randgeschwindigkeit im Anlauf die Wärme schneller abtransportiert wird als bei ausgebildetem Strömungsprofil bei dem sich die Randgeschwindigkeit auf null abgesenkt hat (Haftbedingung). Der Temperaturgradient an der Wand ist im Anlauf somit größer was einen höheren Wärmeübergang und damit größere Nusselt-Zahlen zur Folge hat.

Bei nicht vollständig ausgebildeter hydrodynamischer Strömung sind größere Nusselt-Zahlen zu erwarten als bei ausgebildeter Strömung!

Für Fluide mit kleinen Prandtl-Zahlen, die definitionsgemäß eine relativ hohe Temperaturleitfähigkeit im Verhältnis zu ihrer Viskosität aufweisen (z.B. flüssige Metalle wie Quecksilber), ist der Einfluss des Anlaufs auf die Nusselt-Zahl hingegen weniger stark ausgeprägt. Denn bei solchen Fluiden wird die Wärme aufgrund der hohen Leitfähigkeit ohnehin sehr rasch von der Wand abgeleitet; der Einfluss des Geschwindigkeitsprofils spielt dabei nicht die entscheidende Rolle.

Umgekehrt bedeutet dies aber, dass bei Fluiden mit relativ großen Prandtl-Zahlen, der Einfluss des Anlaufs relativ stark ausgeprägt ist. Um dieser Tatsache gerecht zu werden, ergänzt man die Gleichungen (\ref{nu_lg}) und (\ref{nu_ll}) deshalb um die rot markierten Terme, die explizit abhängig von der Prandtl-Zahl sind.

Für die lokale Nusselt-Zahl gilt unter Berücksichtigung des hydrodynamischen und thermischen Anlaufs:

\begin{align}
&\boxed{Nu= \sqrt[3]{49,371 + \left(1,077 \cdot \sqrt[3]{\beta}-0,7 \right)^3 + \color{red}{\sqrt{\frac{0,03125}{1+22 \cdot Pr}\cdot \beta^3}} } } \\[5px]
&\text{mit}~~~\beta=Re \cdot Pr \cdot \frac{d}{x}\\[5px]
\end{align}

Für die Berechnung der mittleren Nusselt-Zahl gilt folgende Formel:

\begin{align}
&\boxed{\overline{Nu}= \sqrt[3]{49,371 + \left(1,615 \cdot \sqrt[3]{\beta}-0,7 \right)^3 + \color{red}{\sqrt{\frac{2}{1+22 \cdot Pr}\cdot \beta^3}} } } \\[5px]
&\text{mit}~~~\beta=Re \cdot Pr \cdot \frac{d}{l}\\[5px]
\end{align}

Dadurch, dass in den oberen Gleichungen der Profilfaktor im rot markierten Term mit der dritten Potenz in die Berechnung der Nusselt-Zahl eingeht, strebt dieser Term für große Werte von x bzw. l rasch gegen Null. Somit nähern sich die Nusselt-Zahlen immer mehr den Nusselt-Zahlen für eine hydrodynamisch ausgebildete Rohrströmung nach Gleichung (\ref{nu_ll}) bzw. (\ref{nu_lg}) an.

Berücksichtigung der Wärmestromrichtung und der Temperaturabhängigkeit der Stoffwerte

Da die Prandtl-Zahlen für Flüssigkeiten relativ stark von der Temperatur abhängig sind, macht es wieder einen Unterschied, ob das Fluid Wärme auf das Rohr überträgt oder ob das Rohr Wärme auf das Fluid überträgt. Je nachdem erhält man im Fluid unterschiedliche Temperaturverläufe, die Auswirkungen auf die Prandl-Zahlen haben.

Hufschmidt und Burck (International Journal of Heat and Mass Transfer, 1968) geben deshalb einen Korrekturfaktor an, mit dem die Richtung des Wärmestroms bzw. die Temperaturabhängigkeit der Stoffwerte berücksichtigt wird. Dieser Faktor ist wie folgt auf die zuvor berechneten mittleren Nusselt-Zahlen anzuwenden:

\begin{align}
\label{temp}
&\boxed{\overline{Nu}^*= \overline{Nu} \cdot \left(\frac{Pr}{Pr_W}\right)^{0,11} } ~ \text{gilt für Flüssigkeiten}\\[5px]
\end{align}

Die Prandtl-Zahl Pr bezieht sich dabei auf die mittlere Flüssigkeitstemperatur, während sich die Prandtl-Zahl Pr_W auf die Stoffwerte bei Wandtemperatur bezieht.

Aufgrund der relativ geringen Auswirkungen der Temperaturabhängigkeit im Falle von strömenden Gasen, entfällt dort meist ein Korrekturfaktor. Der Temperatureinfluss gibt der VDI Wärmeatlas (7. Auflage, 1994) für Luft, Stickstoff und Helium mit weniger als 10 % an, solange sich die Gas- und Wandtemperaturen nicht mehr als Faktor 2 voneinander unterscheiden (in der Einheit Kelvin gerechnet!).

Laminare Rohrströmung bei konstanter Wärmestromdichte

Hydrodynamisch ausgebildete Strömung (lange Rohre)

Im Folgenden betrachten wir das Strömen eines Fluids durch ein Rohr mit einer konstanten Wärmestromdichte bei ausgebildeter hydrodynamischer Strömung. Ein solcher Fall liegt bspw. bei elektrisch beheizten Rohren vor, denen eine entsprechende Vorlaufstrecke vorangeschalten ist. Für die lokale Nusselt-Zahl an einer Position x, gemessen ab Beginn der Beheizung oder Kühlung, gilt:

\begin{align}
\label{96}
&\boxed{Nu= \sqrt[3]{84,11 + \left(1,302 \cdot \sqrt[3]{\beta}-1 \right)^3} } \\[5px]
& \beta=Re \cdot Pr \cdot \frac{d}{x}\\[5px]
\end{align}

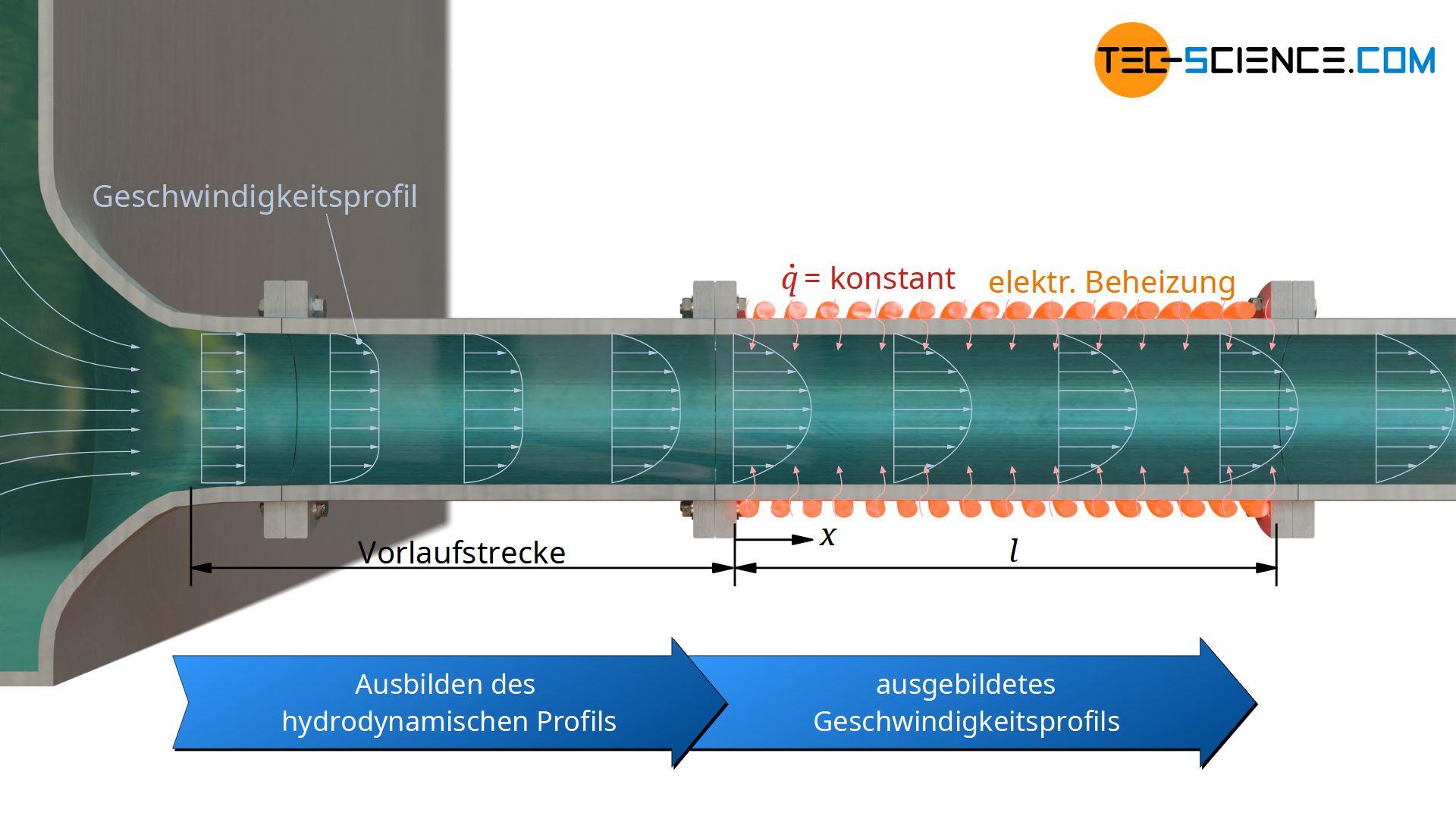
Die Integration der lokalen Nusselt-Zahlen über die gesamte Rohrlänge hinweg, ergibt schließlich die mittlere Nusselt-Zahl, welche sich auch mit folgender Formel ermitteln lässt:

\begin{align}
\label{97}
&\boxed{\overline{Nu}= \sqrt[3]{83,326 + \left(1,953 \cdot \sqrt[3]{\overline{\beta}}-0,6 \right)^3} } \\[5px]
&\overline{\beta}=Re \cdot Pr \cdot \frac{d}{l}\\[5px]
\end{align}

Auch an dieser Stelle sei wieder angemerkt, dass für lange Rohre die Profilfaktoren gegen Null gehen. Die Nusselt-Zahlen nähern sich in diesen Fällen der konstanten Nusselt-Zahl von 4,364 an [siehe Gleichung (\ref{4364})]:

\begin{align}
& \lim \limits_{l \to \infty}\beta \rightarrow 0 ~~~\Rightarrow~~~ Nu\rightarrow 4,364 \\[5px]
\end{align}

Berücksichtigung des hydrodynamischen Anlaufs (kurze Rohre)

Auch unter der Bedingung der konstanten Wärmestromdichte muss der hydrodynamische Anlauf wieder berücksichtigt werden, sofern ein solcher vorhanden ist. Für Prandtl-Zahlen größer 0,7 gelten für die lokale bzw. mittlere Nusselt-Zahl die folgenden Formeln zur Berechnung:

\begin{align}
&\boxed{\overline{Nu}= 0,924 \cdot Pr^{-\frac{1}{6}} \cdot \sqrt{\overline{\beta}}} ~&&\overline{\beta}=Re \cdot Pr \cdot \frac{d}{l}\\[5px]
&\boxed{Nu= 0,462\cdot Pr^{-\frac{1}{6}} \cdot \sqrt{\beta}} ~&&\beta=Re \cdot Pr \cdot \frac{d}{x}\\[5px]
&Pr>0,7
\end{align}

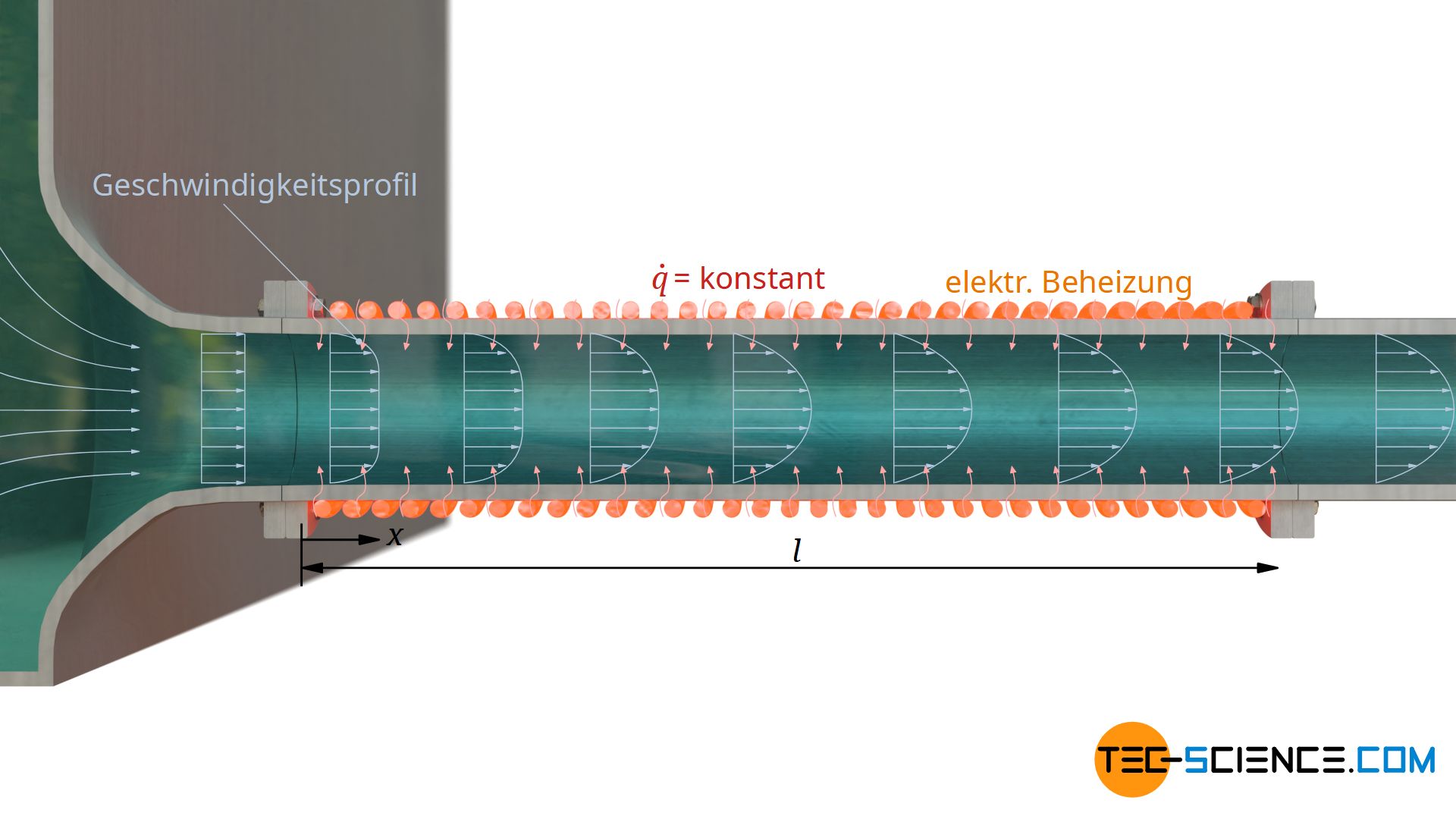
Auch dabei gilt wieder, dass sich die berechneten Nusselt-Zahlen für große Werte von x bzw. l zunächst immer mehr den Werten aus Gleichung (\ref{96}) bzw. (\ref{97}) annähern, da der Einfluss des Anlaufs mehr und mehr vernachlässigbar wird. Wie man allerdings auch erkennen kann, konvergieren die unter Berücksichtigung des Anlaufs erhaltenen Nusselt-Zahlen für weiter steigende Werte von x und l gegen Null. Dies ergibt allerdings wenig Sinn, denn der Grenzwert für die Nusselt-Zahlen liegt gemäß Gleichung (\ref{4364}) bei 4,364.

Die oberen Formeln sind also nur gültig, solange sie größere Werte liefern als die Berechnungen mit den Formeln (\ref{96}) bzw. (\ref{97}). Werden kleinere Werte erhalten, dann ist auch bei Berücksichtigung des hydrodynamischen Anlaufs mit den Gleichungen (\ref{96}) bzw. (\ref{97}) zu rechnen!

Berücksichtigung der Wärmestromrichtung und temperaturabhängigen Stoffwerte

Für Flüssigkeiten wird der Einfluss der temperaturabhängigen Stoffwerte auf die mittlere Nusselt-Zahl an dieser Stelle wieder nach Gleichung (\ref{temp}) berücksichtigt. Für Gase bleibt der Einfluss wiederum meist vernachlässigbar.

Turbulente Rohrströmung

Bei turbulenten Rohrströmungen durchmischt sich das Fluid auch im Randbereich sehr stark, sodass in der Praxis keine Unterscheidung in der Berechnung der Nusselt-Zahlen zwischen konstanter Wandtemperatur und konstanter Wärmestromdichte gemacht werden muss.

Die Turbulenz der Strömung beeinflusst in diesem Zusammenhang maßgeblich den Wärmeübergang und somit die Nusselt-Zahl. Die Rauigkeit der Rohrwand spielt dabei eine entscheidende Rolle, was wiederum Auswirkungen auf den Druckverlust innerhalb der Rohrleitung hat. Man gibt deshalb die Nusselt-Zahl in Abhängigkeit des Druckverlustbeiwertes ζ an.

Für die mittleren Nusselt-Zahlen über das gesamte Rohr hinweg gilt nach Gnielinski (Neue Gleichungen für den Wärme- und den Stoffübergang in turbulent durchströmten Rohren und Kanälen. Forschung im Ingenieurwesen 41, 1975) und Filonenko (Hydraulischer Widerstand von Rohrleitungen, 1954) folgende Formel zur Berechnung:

\begin{align}
&\boxed{\overline{Nu} = \frac{\frac{\zeta}{8} \cdot (Re-1000) \cdot Pr}{1+12,7 \cdot \sqrt{\frac{\zeta}{8}} \cdot (Pr^\frac{2}{3}-1 )} \cdot \left[1+\left(\frac{d}{l}\right)^\frac{2}{3}\right]} \\[5px]
&\text{mit}~~~\boxed{\zeta=\left(1,82\cdot \log_{10}(Re) -1,64\right)^{-2}} \\[5px]
\end{align}

Sind Druckverlustbeiwerte nicht bekannt, dann können für die mittleren Nusselt-Zahlen auch die folgenden Formeln für überschlägige Berechnungen verwendet werden:

\begin{align}
&\boxed{\overline{Nu} = 0,0214 \left(Re^{0,8}-100 \right)\cdot Pr^{0,4}\cdot \left[1+\left(\frac{d}{l}\right)^\frac{2}{3} \right]} ~~~0,5<Pr<1,5\\[5px]
&\boxed{\overline{Nu} = 0,0120 \left(Re^{0,87}-280\right)\cdot Pr^{0,4}\cdot \left[1+\left(\frac{d}{l}\right)^\frac{2}{3} \right]} ~~~1,5<Pr<500\\[5px]
\end{align}

Der Abhängigkeit der Stoffwerte von der Temperatur kann für Flüssigkeiten wiederum durch das Verhältnis der Prandtl-Zahlen bei der mittleren Temperatur (Pr) und der Wandtemperatur (Pr_W) berücksichtigt werden:

\begin{align}
&\boxed{\overline{Nu}^*= \overline{Nu} \cdot \left(\frac{Pr}{Pr_W}\right)^{0,11} } ~ \text{gilt für Flüssigkeiten}\\[5px]
\end{align}

Für Gase sind die Prandtl-Zahlen nur relativ gering von der Temperatur abhängig. Den Temperatureinfluss auf den Wärmeübergang berücksichtigt man deshalb direkt über das Verhältnis zwischen mittlerer Gastemperatur T_m und Wandtemperatur T_W:

\begin{align}
&\boxed{\overline{Nu}^*= \overline{Nu} \cdot \left(\frac{T_m}{T_W}\right)^{n} } ~ \text{gilt für Gase}\\[5px]
\end{align}

\begin{align}
&n=0 && \text{für}~~ T_m>T_W ~\text{(Gas wird durch die Wand abgekühlt)}\\[5px]
&n\neq 0 && \text{für}~~T_W>T_m ~\text{(Gas wird durch die Wand erwärmt)}\\[5px]
\end{align}

Für den Fall, dass das Gas Wärme auf die Wand überträgt, d.h. das Gas also gekühlt wird, ist der Einfluss der Temperaturabhängigkeit auf die Nusselt-Zahl relativ gering. Der Exponent wird deshalb Null gesetzt (n=0). Für den Fall, dass die Wand Wärme auf das Gas überträgt, d.h. das Gas also beheizt wird, ist der Exponent stark von der Gasart abhängig. Der Exponent kann je nach Druck- und Temperaturbereich sowohl positiv als auch negativ sein.