Erfahre in diesem Artikel mehr über Anwendungen und Beispiele im Zusammenhang mit dem hydrostatischen Druck.
Hydrostatischer Druck
Im Artikel Druck in Flüssigkeiten wurde das Zustandekommen des hydrostatischen Druck und dessen Berechnung ausführlich erläutert. Es wurde gezeigt, dass der hydrostatische Druck ph neben der Dichte der Flüssigkeit ϱ und der Fallbeschleunigung g nur von der Tiefe h unterhalb der Flüssigkeitsoberfläche abhängig ist:
\begin{align}
\label{h}
&\boxed{p_h =\rho \cdot g \cdot h} \\[5px]
\end{align}
In den folgenden Abschnitten soll die Bedeutung des hydrostatischen Druck für den Alltag näher erläutert werden.
Fassversuch von Blaise Pascal
Folgendes Experiment, das angelehnt ist an den Versuch von Blaise Pascal im 17. Jahrhundert, demonstriert eindrucksvoll die bloße Abhängigkeit des hydrostatischen Druck von der Tiefe. Hierzu wird ein großes Glasgefäß vollständig mit Wasser gefüllt. Der (hydrostatische) Wasserdruck, der am Flaschenboden herrscht, kann mit Gleichung (\ref{h}) ermittelt werden. Wird von einer Flaschenhöhe von einem halben Meter ausgegangen, dann beträgt der hydrostatische Wasserdruck am Boden etwa 0,05 bar. Diesem relativ geringen Wasserdruck kann die Glasflasche noch problemlos standhalten.

Wird nun aber ein vertikal verlaufender Schlauch am Flaschenhals angebracht und mit Wasser gefüllt, dann steigt aufgrund der Zunahme der Wasserhöhe der hydrostatische Druck an. Wird der Schlauch bspw. über mehrere Stockwerke eines Gebäudes geführt, dann kann der Druck hierdurch sehr stark ansteigen. Bei einer Höhe von 30 Metern steigt der Wasserdruck damit auf über 3 bar an. Schließlich wird der Wasserdruck irgendwann so groß sein, dass die Glasflasche den enormen Kräften nicht mehr stand halten kann und zerbricht.
Das Eindrucksvolle an diesem Experiment ist, dass es dabei keine Rolle spielt, welchen Innendurchmesser der Schlauch hat, solange Kapillareffekte vernachlässigt werden können. Ein Schlauch mit einem Innendurchmesser von 4 mm reicht theoretisch völlig aus. Um diesen Schlauch mit Wasser zu befüllen sind knapp 380 ml Wasser nötig. 380 ml Wasser reichen also völlig aus, um den Wasserdruck in der Glasflasche um das über 60-fache ansteigen zu lassen; unabhängig davon welches Fassungsvermögen das Glas hat!
Wasserdruck im Meer
Der hydrostatische Druck führt dazu, dass der Wasserdruck in Gewässern mit zunehmender Tiefe mehr und mehr zunimmt. Mit einer Wasserdichte von rund 1000 kg/m³ und einer Fallbeschleunigung von etwa 10 N/kg erhält man somit pro 10 Meter Wassertiefe eine Zunahme des Wasserdrucks um ca. 1 bar. Beachte, dass sich die Druckangaben in der unteren Abbildung lediglich auf den hydrostatischen Druck beziehen (kurz als Wasserdruck bezeichnet). Für den Gesamtdruck in einer bestimmten Tiefe muss der auf der Wasseroberfläche lastenden Umgebungsdruck von 1 bar noch hinzu addiert werden.

Der Wasserdruck steigt um etwa 1 bar pro 10 Meter Wassertiefe!
Der zunehmende Wasserdruck führt bei Tauchgängen bspw. dazu, dass mit zunehmender Tiefe mehr Luft aus den mitgeführten Pressluftflaschen eingeatmet werden muss. Denn um den umgebenden Wasserdruck auszugleichen, muss die Lunge durch die eingeatmete Luft denselben Druck erzeugen, ansonsten würde die Lunge durch den größeren Wasserdruck zusammengedrückt werden. Ein größerer Lungendruck kann nur dadurch erreicht werden, dass mehr Luft eingeatmet wird; analog zu einem Fahrradreifen, in den mehr Luft hinein gepumpt werden muss, um den Druck zu erhöhen. Der Luftvorrat in den Pressluftflaschen wird also umso schneller zu Ende gehen, je tiefer man taucht.
Gießkanne
Die Tatsache, dass der hydrostatische Druck nur von der Tiefe abhängig ist, zeigt sich im Alltag an vielen Stellen. Er ist auch der Grund dafür, weshalb sich in Gefäßen, die über Rohre miteinander verbunden sind (sog. kommunizierende Röhren), überall derselbe Wasserspiegel einstellt. Dies zeigt sich im Alltag bspw. an einer Gießkanne, die mit Wasser gefüllt wird. Mit der Zeit wird sich im Gießrohr (auch Tülle genannt) derselbe Wasserpegel einstellen wie in der Kanne selbst.

Als kommunizierende Röhren werden mit Flüssigkeit gefüllte Gefäße bezeichnet, die über Rohre miteinander verbunden sind und sich dabei ein gemeinsamer Flüssigkeitsspiegel einstellt!
Dies kann wie folgt mathematisch erklärt werden. Das Wasser in der Kanne führt in der Tiefe hK, wo die Tülle angeschweißt ist, zu einem bestimmten hydrostatischen Druck pK:
\begin{align}
&p_{K} =\rho \cdot g \cdot h_{K} ~~~\text{hydrostatischer Druck in der Kanne} \\[5px]
\end{align}
Auf die analoge Weise kann man den hydrostatischen Druck im Gießrohr pR in der Tiefe hR unterhalb des Wasserspiegels ermitteln:
\begin{align}
&p_{R} =\rho \cdot g \cdot h_{R} ~~~\text{hydrostatischer Druck im Rohr} \\[5px]
\end{align}
Dabei werden während des Befüllens der Kanne durchaus unterschiedliche Wasserhöhen zwischen Kanne und Gießrohr zu beobachten sein. Denn schließlich wird das Wasser im Gießrohr ja durch den größeren Wasserdruck in der Kanne nach oben gedrückt.
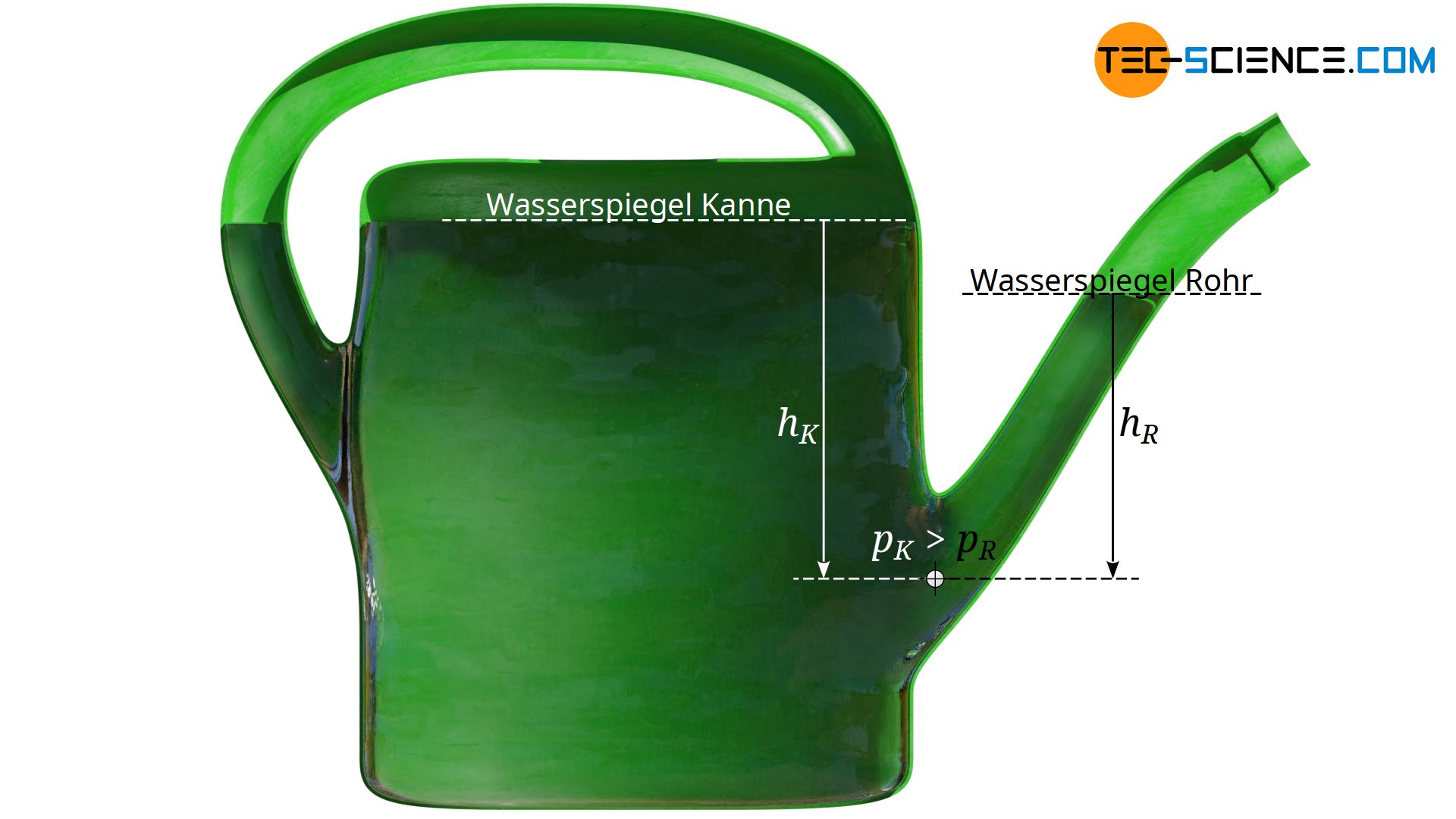
Nach dem Einfüllen stellt sich aber ein Gleichgewichtszustand ein und das Wasser wird nicht weiter durch das Rohr gedrückt. In diesem Fall muss offensichtlich der hydrostatische Druck, der durch die Wassersäule im Gießrohr verursacht wird, genauso groß sein wie der hydrostatische Druck, den die Wassersäule in der Kanne verursacht. Wäre dies nicht der Fall, dann würde der größere der beiden hydrostatischen Drücke entweder das Wasser in der Kanne oder im Gießrohr weiter nach noch oben drücken. Im Gleichgewichtszustand müssen also unweigerlich die hydrostatischen Drücke gleich sein, was letztlich nur bei einem gemeinsamen Wasserspiegel der Fall ist:
\begin{align}
\require{cancel}
p_{K} &\overset{!}{=} p_{R} \\[5px]
\bcancel {\rho \cdot g} \cdot h_{K} &= \bcancel{\rho \cdot g} \cdot h_{R} \\[5px]
h_{K} &= h_{R} \\[5px]
\end{align}
Dass sich im (statischen) Gleichgewichtszustand identische hydrostatische Drücke einstellen, zeigt auch bereits die Tatsache, dass Drücke in Flüssigkeiten im Gegensatz zu Auflagedrücken in alle Richtungen gleichermaßen wirken. Es kann in einer bestimmten Tiefe also nicht zwei unterschiedliche hydrostatischen Drücke geben. Wäre dies nämlich der Fall, dann käme es zu Strömungen und es wäre kein statisches Gleichgewicht vorhanden.
Schlauchwaage
Dass sich in Gefäßen, die miteinander verbunden sind, identische Wasserspiegel einstellen, wird technisch in sogenannten Schlauchwaagen genutzt. Dabei sind zwei Gefäße mit jeweils einer Maßeinteilung versehen und über einen Schlauch miteinander verbunden. Im Schlauch befindet sich Wasser. Der Wasserstand kann an den Skalen abgelesen werden.

Da sich in beiden Gefäßen derselbe Wasserstand einstellt, kann auf diese Weise auch über große Distanzen hinweg, wo einfache Wasserwaagen nicht mehr eingesetzt werden können, sehr einfach eine gleiches Höhenniveau eingestellt werden. Eingesetzt werden Schlauchwaagen bspw. in der Bautechnik, wobei heutzutage meist elektronische Sensoren zur Anwendung kommen.

Wasserturm
Eine weitere technische Umsetzung, das den hydrostatischen Druck bzw. das Streben nach einem gemeinsamen Flüssigkeitsspiegel in kommunizierenden Röhren nutzt, ist der Wasserturm.

Bei einem Wasserturm handelt es sich im Prinzip um einen Hochbehälter, der durch Pumpen mit Wasser befüllt wird. Durch den entstehenden hydrostatischen Druck, kann das Wasser ohne zusätzliche Pumpen in die tiefer gelegenen Haushalte gedrückt werden. Durch das große Wasserreservoir im Turm von meist mehreren Millionen Litern, sinkt der Wasserspiegel nur relativ langsam. Dies gewährleistet einen nahezu gleichbleibenden Wasserdruck, bevor bei Unterschreiten eines bestimmten Grenzwertes wieder Wasser nachgepumpt wird.
Heutzutage werden Wassertürme allerdings immer seltener genutzt. In der modernen Wasserversorgung kommen meist Pumpen genutzt, die das Wasser direkt zu den Verbrauchern befördern.






