Grundlage der Kraftübertragung im Riementrieb ist die Gleichung nach Euler und Eytelwein (Eulersche-Eytelweinsche Seilreibungsgleichung).
Kräfte an einer feststehenden Riemenscheibe
Im Artikel Wie funktioniert ein Riementrieb? wurde bereits erläutert, dass die Kraftübertragung bei Riementriebe auf Reibungskräfte zwischen Riemen und Scheibe zurückzuführen sind (Ausnahme: Zahnriemen). In diesem Abschnitt sollen die physikalischen Grundlagen hierzu näher diskutiert werden.
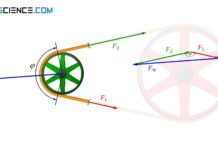
Um die Kräfteverhältnisse am Riementrieb besser zu verstehen, wird zunächst eine feststehende Riemenscheibe betrachtet, um die ein offener Riemen gelegt wird. Man stelle sich hierzu eine Person vor, die die Riemenscheibe am Umfang festhält.
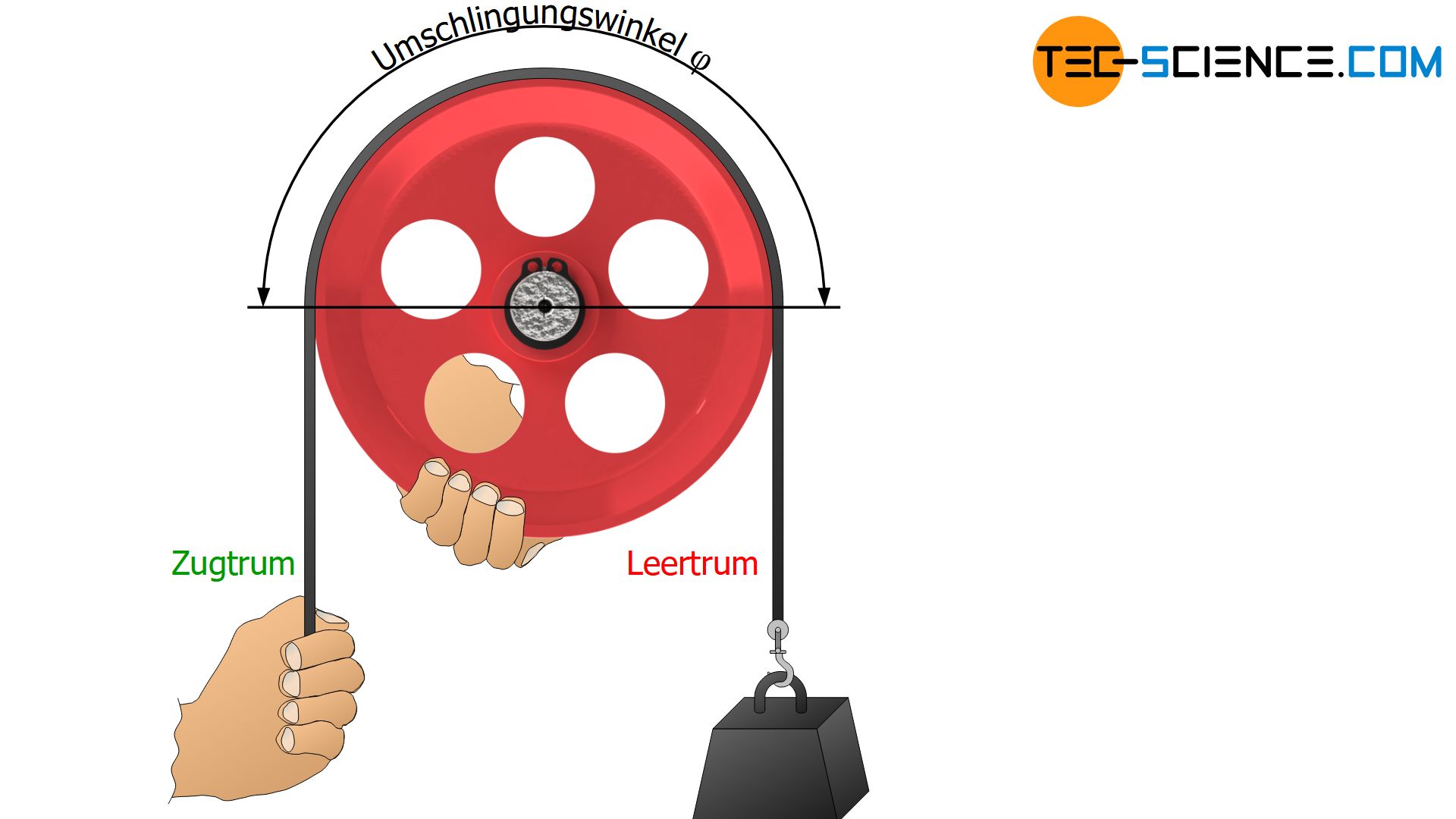
An einem Ende des Riemens wird mit einer bestimmten Kraft FL gehalten („Leertrumskraft“). Diese Halten kann im Prinzip auch einfach eine angehängte Last sein. Am anderen Ende des Riemens zieht nun eine Person mit zunehmender Kraft, bis jener Punkt erreicht ist, in dem der Riemen gerade noch nicht über die feststehende Scheibe rutscht. In diesem Zustand wirkt somit die maximal mögliche Zugkraft FZ,max im Riemen („Zugtrumskraft“). Ein vermeintlich stärkeres Ziehen würde nämlich dazu führen, dass die Haftreibung überwinden wird und der Riemen über die Scheibe rutscht. Dann wäre jedoch nicht mehr die Haftreibung aktiv sondern die deutlich geringere Gleitreibung, was wiederum eine verringerte Zugkraft zur Folge hat.
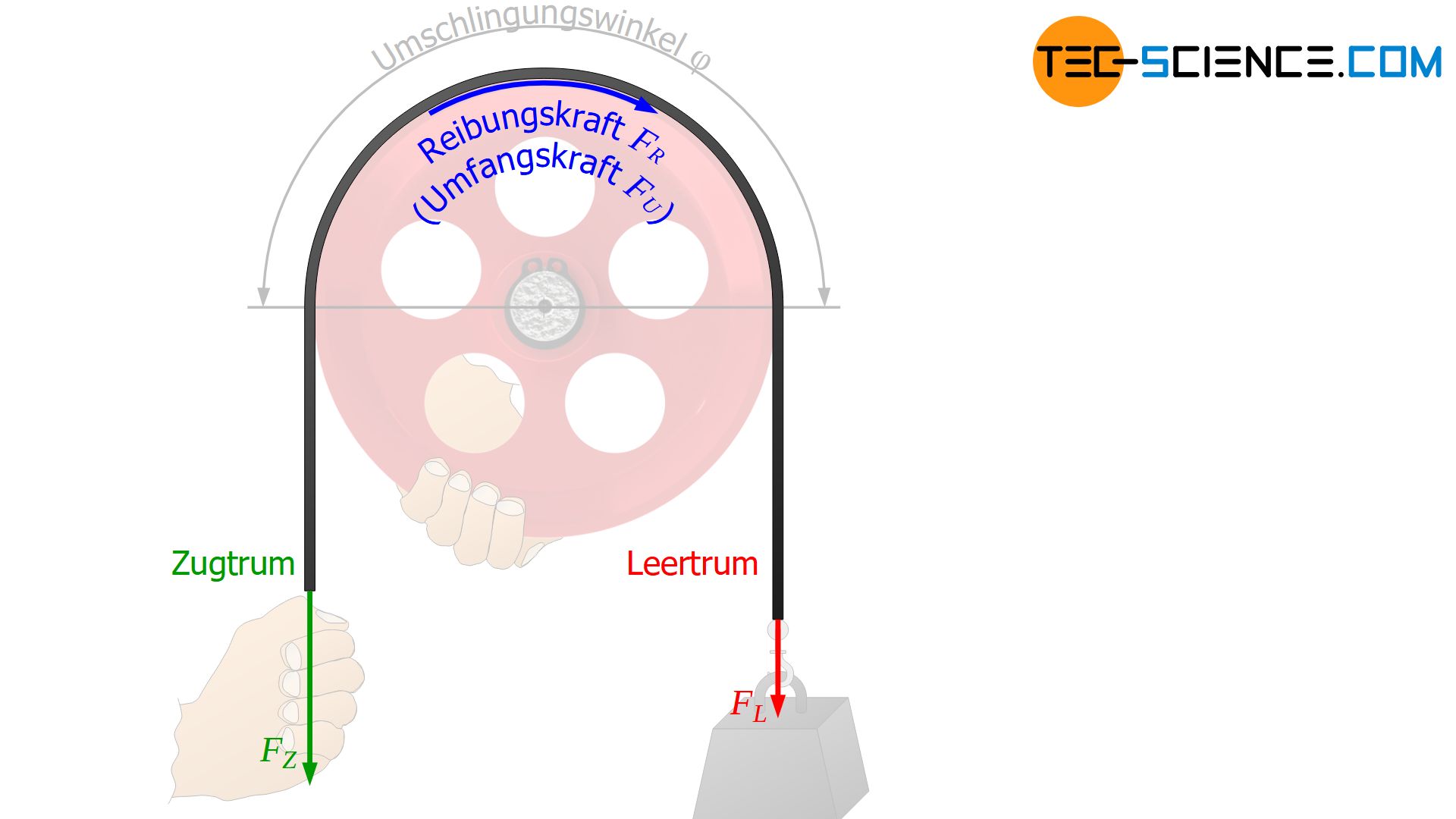
Im Grenzfall des statischen Gleichgewichtes (d.h. unmittelbar bevor der Riemen ins Rutschen kommt), muss auf der Zugseite also nicht nur die Haltekraft aufgebracht werden sondern es kann zusätzlich noch so stark gezogen werden wie die Reibungskraft maximal werden kann. Die Summe aus Leertrumskraft FL und maximal wirkender Reibungskraft FR,max entspricht somit der maximal möglichen Zugtrumskraft FZ,max im statischen Gleichgewicht:
\begin{align}
&F_{Z,max} =F_L + F_{R,max} \\[5px]
\label{zugkraft}
&\boxed{F_{R,max} =F_{Z,max} – F_L} \\[5px]
\end{align}
Eulersche-Eytelweinsche Seilreibungsgleichung
Die Wissenschaftler Euler und Eytelwein beschäftigten sich bereits im 18. Jahrhundert mit den wirkenden Kräften an den Enden eines Seiles, die um runde Gegenstände geschlungen werden (z.B. Schiffsseil um einen Poller). Im statischen Grenzfall konnten die Physiker einen eindeutigen Zusammenhang zwischen der Haltekraft auf der einen Seite („Leertrumskraft“ FL) und der maximal möglichen Zugkraft auf der anderen Seite („Zugtrumskraft“ FZ,max) herstellen.
Dieser Zusammenhang geschieht zum einen über den Reibungskoeffizienten µ (auch Reibwert oder Reibzahl genannt) und zum anderen über den Umschlingungswinkel φ, denn bei vorgegebener Haltekraft beeinflussen beide Größen im selben Maße die maximal mögliche Zugkraft:
- Umso größer der Reibungskoeffizient, desto stärker die Reibung und umso größer die maximale Zugkraft
- umso größer der Umschlingungswinkel desto stärker die Reibung und umso größer die maximale Zugkraft
Mathematisch führten die Überlegungen von Euler und Eytelwein auf folgende, nach ihnen benannte Seilreibungsgleichung:
\begin{align}
\label{eytelwein}
&\boxed{F_{Z,max} =F_L \cdot e^{\mu \cdot \varphi}} ~~~\text{Seilreibungsgleichung}\\[5px]
\end{align}
Die Euler-Eytelweinsche Seilreibungsgleichung ist nur im statischen Grenzfall gültig ist, d.h. wenn die maximal mögliche Zugkraft und damit die maximal mögliche Reibung wirkt, bevor das Seil zu Rutschen beginnt!
Losgelassene Riemenscheibe
Die Seilreibungsgleichung kann schließlich auch auf den Riementrieb angewendet werden. Anstelle eines Seils welches um einen Poller gelegt wird, umschlingt nun ein Riemen eine Riemenscheibe.
Gemäß dieser Gleichung kann bei gegebener Kaft im Leertrum FL somit am Zugtrum maximal mit der Kraft FZ,max = FL⋅eµφ gezogen werden, ohne dass der Riemen von der feststehenden Riemenscheibe rutscht.
Über die in diesem Zustand maximal wirkende Reibungskraft FR,max versucht der Riemen also dabei die noch feststehende Scheibe in Rotation zu versetzen. Dies Kraft verspürt auch die Person, die die Riemenscheibe am Umfang festhält. Die Reibungskraft wirkt somit als Umfangskraft, mit der die Scheibe versucht zu rotieren.
Wird die Riemenscheibe in diesem Zustand losgelassen, dann wird sie folglich mit dieser Umfangskraft bzw. mit der maximal möglichen Reibungskraft FR,max angetrieben. Dies entspricht nach Gleichung (\ref{zugkraft}) gerade der Differenz der Kräfte FZ und FL:
\begin{align}
&F_{R,max} = F_{Z,max} – F_L \\[5px]
\end{align}
Die maximal mögliche Zugkraft FZ,max steht über die Seilreibungsgleichung (\ref{eytelwein}) in eindeutigem Zusammenhang zur Leertrumskraft FL, sodass für die scheibenantreibende Reibungskraft schließlich gilt:
\begin{align}
\label{reibungskraft}
&\boxed{F_{R,max} =F_L \cdot \left(e^{\mu \cdot \varphi} -1 \right)} ~~~\text{maximal mögliche (antreibende) Reibungskraft} \\[5px]
\end{align}
Diese Gleichung beschreibt die maximal wirksame Reibungskraft FR,max mit der die Riemenscheibe bei gegebener Leertrumskraft FL angetrieben werden kann, ohne dass der Riemen dabei durchrutscht.
Interpretation
Aus Gleichung (\ref{reibungskraft}) folgt direkt, dass zwingend eine Kraft im Leertrum vorhanden sein muss, wenn eine antreibende Reibungskraft zwischen Riemen und Scheibe zustande kommen soll! Ist keine Kraft im Leertrum vorhanden (FL=0), dann können Reibungskoeffizient und Umschlingungswinkel noch so groß sein, die Reibungskraft wird zu Null und die Riemenscheibe kann nicht angetrieben werden.
Das zwingend notwendige Vorhandensein einer Leertrumskraft zur Kraftübertragung lässt sich im vorliegenden Beispiel auch direkt aus der Erfahrung heraus erklären. Stellt man sich nämlich vor, dass auf der Leertrumsseite das Gewicht fehlt, dann würde man beim Ziehen lediglich das Seil ohne großen Kraftaufwand (und damit ohne große kraftübertragende Reibungskraft) locker über die Scheibe ziehen. Die Person, die die Scheibe am Umfang festhält, würde kaum eine Umfangskraft wahrnehmen.
Es fehlt in diesem Fall nämlich die notwendige Anpresskraft des Riemens auf die Riemenscheibe, um eine große Reibungskraft und damit Umfangskraft erzeugen zu können. Diese Anpresskraft kann überhaupt erst durch das Gewicht im Leertrum zustande kommen! Nur so können große Reibungskräfte wirken und hohe Kräfte übertragen werden.
Auf Riemengetriebe übertragen würde das Fehlen einer Leertrumskraft letztlich bedeuten, dass der Riemen ohne Spannung ist und sich nicht an die Riemenscheiben pressen kann um die notwendige Reibungskraft zur Kraftübertragung bereitzustellen. Somit ist zwingend eine Kraft im Leertrum (Riemenspannung) erforderlich, wenn eine bestimmte Kraftübertragung gewährleistet werden soll.
Für die Kraftübertragung muss zwingend eine Kraft im Leertrum vorhanden sein, damit die Riemenspannung aufrecht erhalten bleibt und der Riemen an die Scheiben angepresst wird!
Mindestkraft im Leertrum
Wie groß die Leertrumskraft bei gegebener Zugtrumskraft mindestens sein muss, kann ebenfalls aus der Seilreibungsgleichung bestimmt werden. Dabei wird nun davon ausgegangen, dass die Kraft im Zugtrum mit FZ fest vorgegeben ist. Die Fragestellung lautet dann, mit welcher Mindestkraft FL,min\) am Leertrum gehalten werden muss, damit der Riemen bei gegebener Zugtrumskraft FZ gerade nicht mehr über die Scheibe rutscht (Beachte, dass die Zugtrumskraft sozusagen immer der „aktiv“ ziehenden und die Leertrumskraft immer der „passiv“ gezogenen/haltenden Kraft entspricht). Damit wird Gleichung (\ref{eytelwein}) zu:
\begin{align}
&F_{Z} =F_{L,min} \cdot e^{\mu \cdot \varphi} \\[5px]
\label{minimal}
&\boxed{F_{L,min} =F_{Z} \cdot \frac{1}{e^{\mu \cdot \varphi}}} ~~~\text{minimal aufzubringende Leertrumskraft} \\[5px]
\end{align}
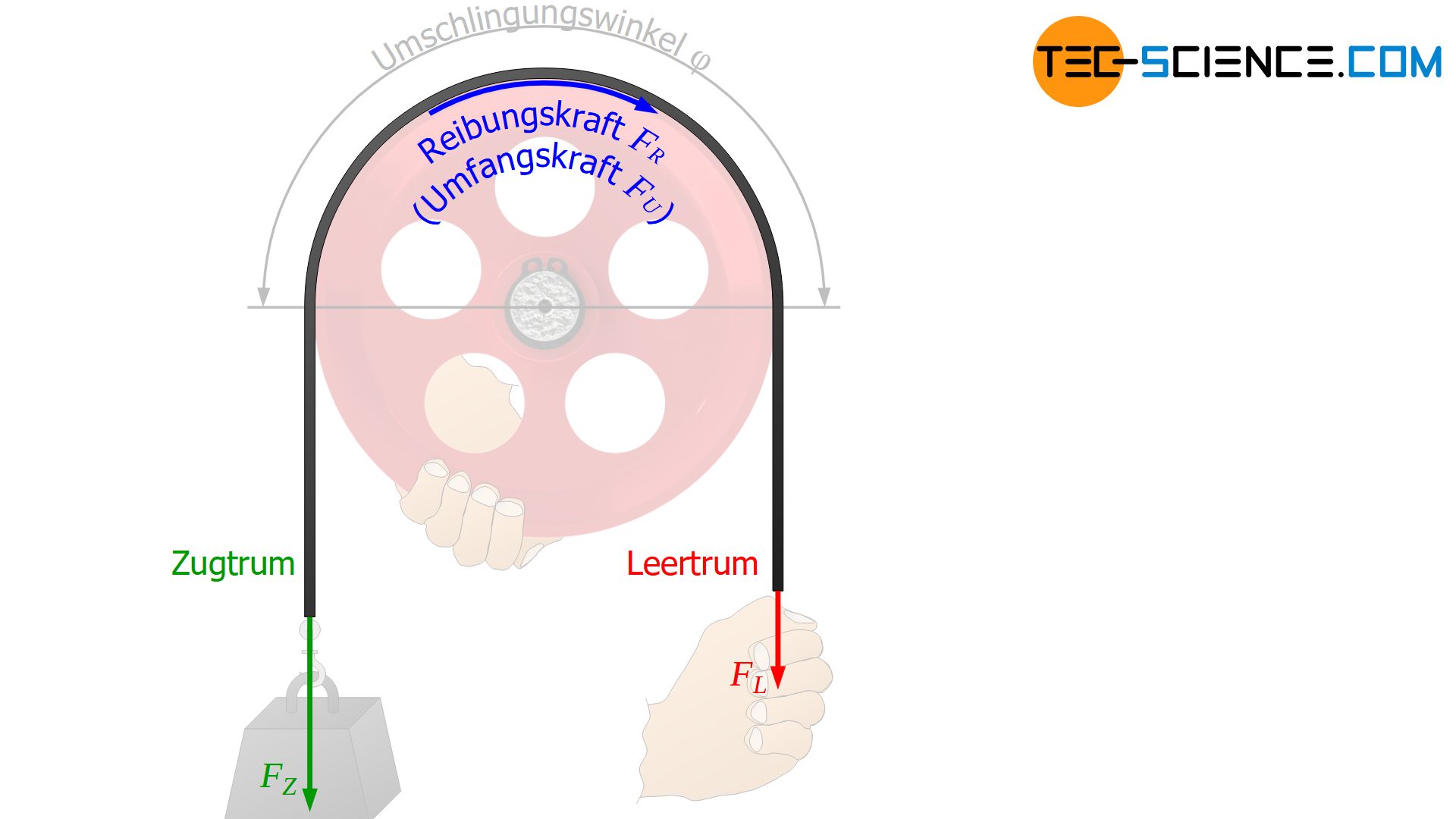
Aus Gleichung (\ref{minimal}) lässt sich nun derselbe Sachverhalt ableiten. Soll eine Kraft im Zugtrum durch den Riemen übertragen werden, damm muss auch unweigerlich eine Mindestkraft FL,min im Leertrum vorhanden sein, ansonsten würde es aufgrund fehlender Riemenspannung zum Abrutschen kommen! Bei dieser Mindestkraft wirkt die maximal antreibende Reibungskraft (da mit der geringst möglichen Kraft entgegen der Zugrichtung gehalten wird). Diese maximale Reibungskraft bestimmt sich analog zu Gleichung (\ref{zugkraft}):
\begin{align}
& F_{R,max} = F_{Z} – F_{L,min} = F_Z – F_Z \cdot \frac{1}{e^{\mu \cdot \varphi}} \\[5px]
\label{123}
&\boxed{F_{R,max} =F_Z \cdot \left(1-\frac{1}{e^{\mu \cdot \varphi}} \right)} ~~~\text{maximal mögliche (antreibende) Reibungskraft} \\[5px]
\end{align}
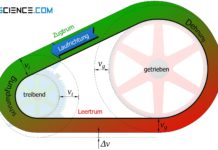
Überlastsicherung
An dieser Stelle zeigt sich auch die Überlastsicherung die Riementriebe. Hierzu wird das im Artikel zuvor vorgestellte Beispiel der Seilwinde nochmals betrachtet. Wenn bspw. die Abtriebsscheibe kaum noch die Seilwinde aufgrund zu hoher Last in Bewegung setzen kann, dann steigt die Zugtrumskraft enorm an, da der Motor weiterhin versucht die Antriebsscheibe zu drehen und mit ihr den Riemen zu bewegen. Der Riemen wird im Zugtrum somit sehr stark gedehnt. Die Antriebsscheibe schiebt den Riemen sozusagen in das Leertrum. Als Folge lässt die Riemenspannung im Leertrum nach, was gemäß Gleichung (\ref{reibungskraft}) unmittelbar zu einer Abnahme der maximal möglichen Reibungskraft führt und die Antriebsscheibe ab einem kritischen Punkt schließlich durchrutschen lässt. Ein solches „Drübergleiten“ des Riemens über die Scheibe wird auch als Gleitschlupf bezeichnet.