Berechnung der Länge von Riemen (Riementriebe)

Erfahre in diesem Artikel wie sich die Länge von Riemen in Riementrieben berechnet.

Für die Konstruktion von Riementrieben ist es notwendig sowohl den Umschlingungswinkel als auch die Riemenlänge bei gegebenen Scheibendurchmessern und Scheibenabständen zu bestimmen. Grundlage hierfür bildet der aufgezogene Zustand des Riemens auf den Riemenscheiben.

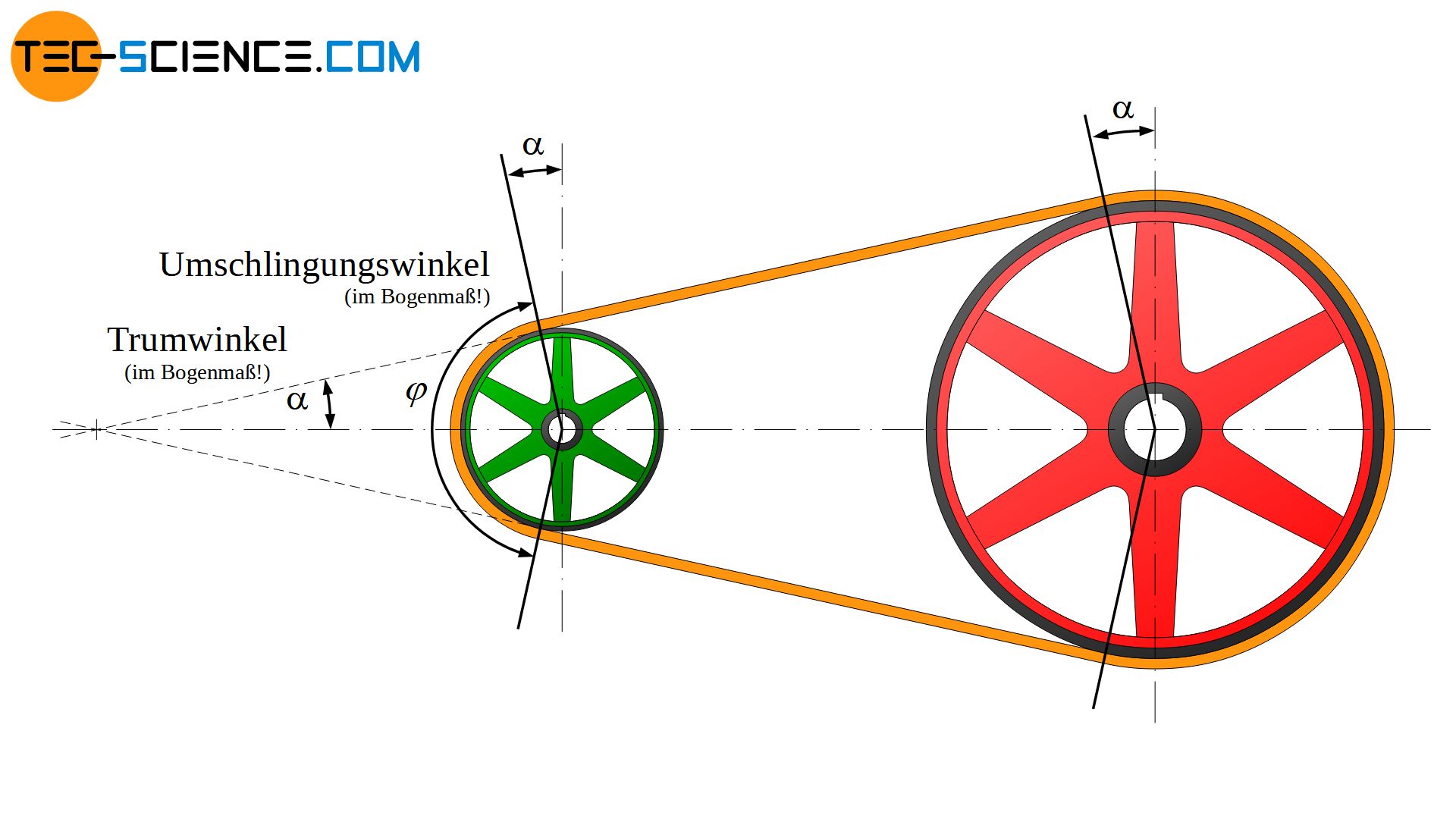
Der Riemen setzt sich dann aus den beiden kreisbogenförmigen Abschnitten b_k und b_g an der kleinen und großen Riemenscheibe zusammen und aus den beiden geradlinigen Trumabschnitten l. Die Summe dieser Riemenabschnitte bilden die geometrische Riemenlänge L_i im aufgezogenen Zustand, wobei sich diese Längenangabe dann auf die Innenseite des Riemens bezieht:

\begin{align}
\label{riemenabschnitte}
&L_i = 2 \cdot l + b_g + b_k \\[5px]
\end{align}

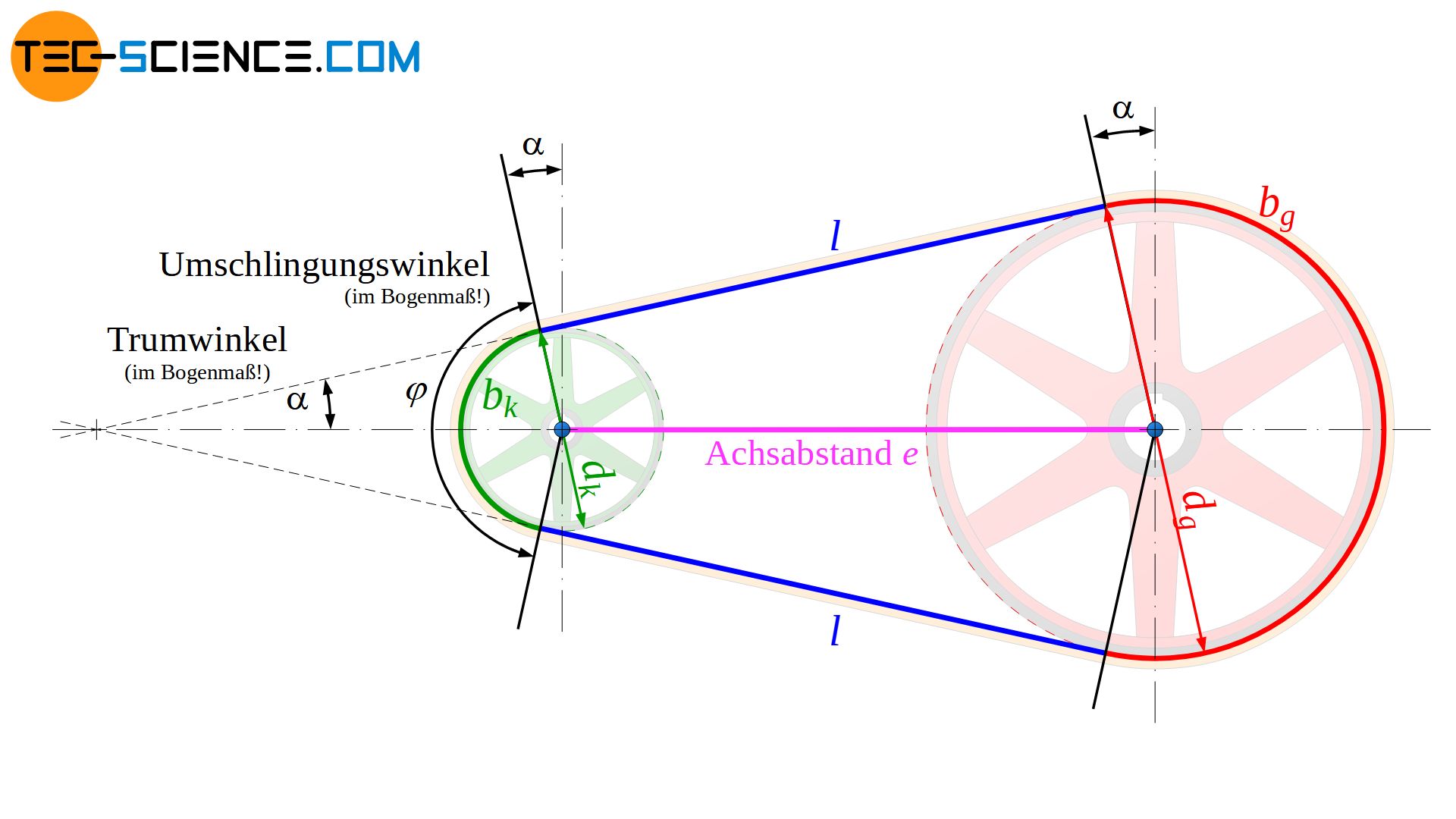
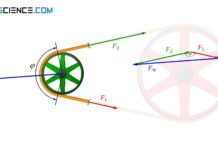
Zunächst soll der Umschlingungswinkel anhand der Scheibendurchmesser und des Scheibenabstandes bestimmt werden. Für die Herleitung wird der  Trumneigungswinkel bzw. Trumwinkel \(\alpha\) genutzt, der sich als Winkel zwischen der Verbindungslinie der Scheibenachsen und dem Trum ergibt. Wie aus der Abbildung oben hervorgeht, stehen der Trumwinkel und der Umschlingungswinkel φ der kleinen Scheibe in folgendem Zusammenhang (sofern nicht ausdrücklich anders erwähnt, beziehen sich die gesamten Winkelangaben und -funktionen auf das Bogenmaß!):

\begin{align}
\label{a_p}
&\boxed{\varphi = \pi – 2 \cdot \alpha} \\[5px]
\end{align}

Nun verschiebt man in Gedanken den geraden Trumabschnitt l entlang der Winkelhilfslinien bis in das Zentrum der kleinen Riemenscheibe. Man erhält hierdurch ein rechtwinkliges Dreieck mit dem Achsabstand e als Hypotenuse und der Trumlänge l als Ankathete, sowie der sich über die Scheibendurchmesser ergebenden Gegenkathete. Der Trumneigungswinkel \(\alpha\) lässt sich dann offensichtlich anhand der Sinusfunktion über die Scheibendurchmesser und den Achsabstand bestimmen:

\begin{align}
&\sin(\alpha) =\frac{d_g-d_k}{2e} \\[5px]
\label{trumneigung}
&\boxed{\alpha =\arcsin\left(\frac{d_g-d_k}{2e}\right)} \\[5px]
\end{align}

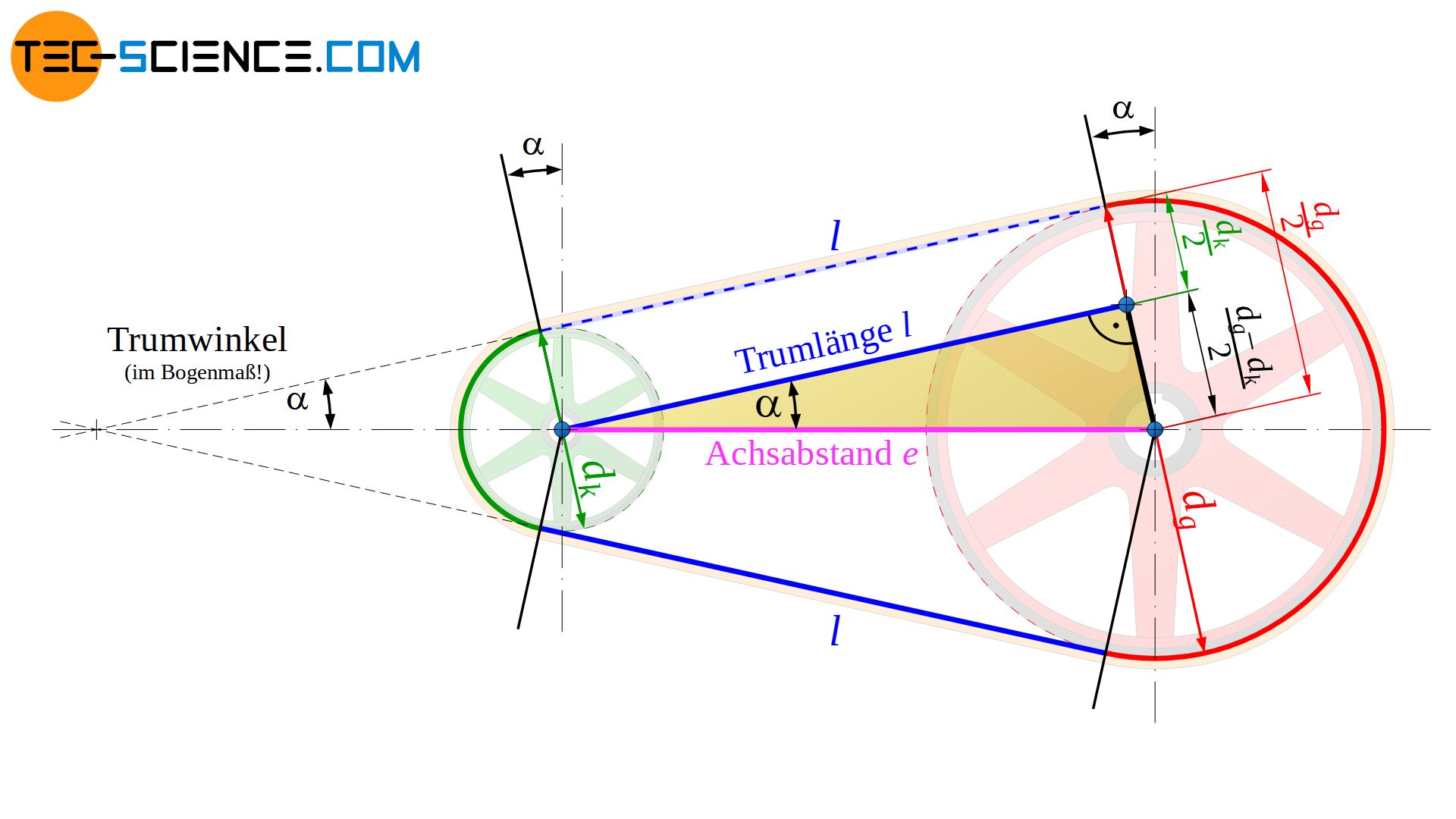
In Kombination mit Gleichung (\ref{a_p}) kann der Umschlingungswinkel φ schließlich wie folgt über die Scheibendurchmesser d_g bzw. d_k und den Achsabstand e ermittelt werden:

\begin{align}
\label{phi}
&\boxed{\varphi = \pi – 2 \cdot \arcsin\left( \frac{d_g-d_k}{2e}\right)} ~~~\text{Bogenmaß!} \\[5px]
\end{align}

Für die Herleitung der Riemenlänge kann zunächst ebenfalls das sich ergebende Dreieck in der oberen Abbildung genutzt werden. So lässt sich über die Kosinusfunktion des Trumwinkels \(\alpha\) die Trumlänge l in Abhängigkeit des Wellenabstands e bestimmen:

\begin{align}
\label{trumlaenge}
&\underline{l = e \cdot \cos(\alpha) } \\[5px]
\end{align}

Zur Ermittlung des Riemenabschnitts um die große Riemenscheibe b_g wird zunächst die Länge des entsprechenden Halbkreises bestimmt (π/2⋅d_g). Dabei müssen jedoch zusätzlich noch die beiden Bogenabschnitte (d_g/2⋅\(\alpha\)) hinzu addiert werden, welche sich durch die Trumneigung mit dem Winkel \(\alpha\) ergeben (Beachte: Bogenwinkel = Bogenlänge/Bogenradius bzw. Bogenlänge = Bogenradius x Bogenwinkel):

\begin{align}
\label{b_g}
&\underline{b_g =\tfrac{\pi}{2}d_g+2 \cdot \tfrac{d_g}{2}\cdot \alpha} \\[5px]
\end{align}

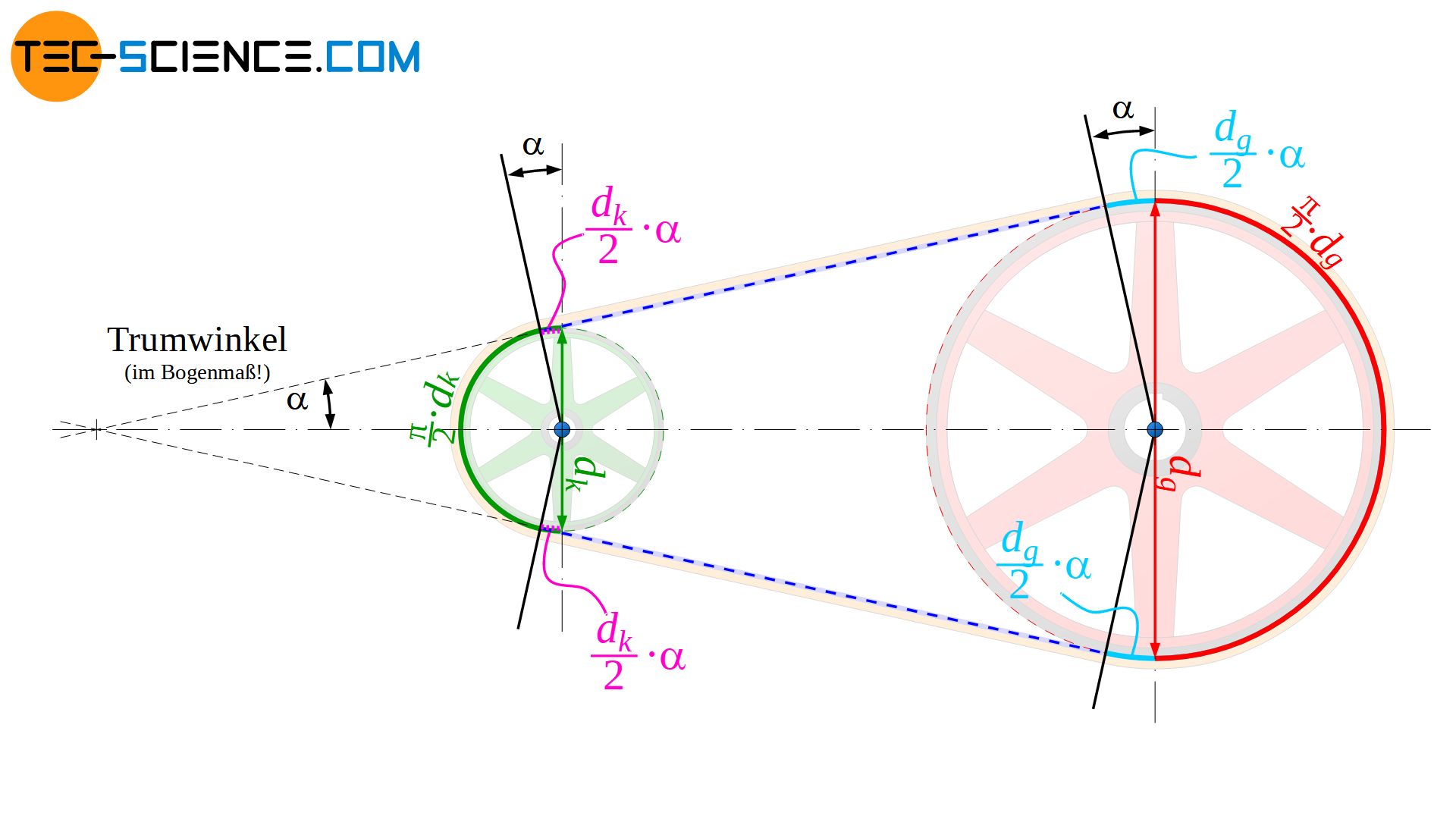
Auf die analoge Weise wird die Bogenlänge des Riemens um die kleine Riemenscheibe b_k bestimmt. Ausgehend der Halbkreislänge π/2⋅d_k müssen aufgrund der Trumneigung dabei jedoch die beiden Bogenlängen d_k/2⋅\(\alpha\) nun subtrahiert werden:

\begin{align}
\label{b_k}
&\underline{b_k =\tfrac{\pi}{2}d_k-2 \cdot \tfrac{d_k}{2}\cdot \alpha} \\[5px]
\end{align}

Mit den Gleichungen (\ref{riemenabschnitte}), (\ref{trumlaenge}), (\ref{b_g}) und (\ref{b_k}) kann nun die Länge der Riemeninnenseite L_i anhand des Trumwinkels \(\alpha\) wie folgt ermittelt werden:

\begin{align}
&L_i = 2 \cdot \underbrace{e \cdot \cos(\alpha)}_{l} + \underbrace{\tfrac{\pi}{2}d_g+2 \cdot \tfrac{d_g}{2}\cdot \alpha}_{b_g} + \underbrace{\tfrac{\pi}{2}d_k-2 \cdot \tfrac{d_k}{2}\cdot \alpha}_{b_k} \\[5px]
\label{riemenlaenge}
&\underline{L_i = 2 \cdot e \cdot \cos(\alpha) + \left(d_g + d_k \right) \tfrac{\pi}{2}+ \left(d_g-d_k \right) \cdot \alpha} \\[5px]
\end{align}

Da der Trumneigungswinkel in der Regel relativ klein ist, können folgende Kleinwinkelnäherungen für das Bogenmaß genutzt werden:

\begin{align}
\label{kleinwinkel}
&\underline{\cos(\alpha) \approx 1 – \frac{\alpha^2}{2}}~~~\text{und} ~~~\sin(\alpha) = \underline{\frac{d_g-d_k}{2e} \approx \alpha} \\[5px]
\end{align}

Damit lässt sich die Riemenlänge in der Praxis mit hinreichender Genauigkeit wie folgt ermitteln:

\begin{align}
&L_i  \approx 2 e \cdot \underbrace{\left(1 – \frac{\alpha^2}{2}\right)}_{\approx \cos(\alpha)} + \left(d_g + d_k \right) \tfrac{\pi}{2}+ \left(d_g-d_k \right) \cdot \underbrace{\frac{d_g-d_k}{2e}}_{\alpha} ~~~~~\text{mit} ~~~\alpha \approx \frac{d_g-d_k}{2e} ~~~\text{folgt:}\\[5px]
&L_i  \approx 2 e \cdot \left(1 – \frac{(d_g-d_k)^2}{8e^2}\right) + \left(d_g + d_k \right) \tfrac{\pi}{2}+ \left(d_g-d_k \right) \cdot \frac{d_g-d_k}{2e} \\[5px]
&L_i  \approx 2 e – \frac{(d_g-d_k)^2}{4e} + \left(d_g + d_k \right) \tfrac{\pi}{2}+ \frac{(d_g-d_k)^2}{2e} \\[5px]
&\boxed{L_i  \approx 2 e  + \tfrac{\pi}{2} \left(d_g + d_k \right)  + \tfrac{1}{4e} (d_g-d_k)^2} \\[5px]
\end{align}

Diese Formel bietet nicht nur den Vorteil, dass sie relativ übersichtlich ist und ohne Trumwinkel auskommt sondern durch Umstellen kann nun auch bei gegebener Riemenlänge L_i der Wellenabstand e ermitellt werden. Nach mathematischen Umformungen und Anwendung der „p-q-Formel“ folgt:

\begin{align}
& \boxed{e \approx \tfrac{1}{4} L_i – \tfrac{\pi}{8} \cdot (d_g+d_k) + \sqrt{ \left[ \tfrac{1}{4} L_i – \tfrac{\pi}{8} \cdot (d_g+d_k) \right]^2 – \tfrac{1}{8}(d_g-d_k)^2 }}
\end{align}

Für Flachriemen sollte der Wellenabstand nach Norm zwischen folgenden Grenzwerten eingestellt werden:

\begin{align}
& \boxed{0,7 \cdot (d_g+d_k) \le e \le 2 \cdot (d_g+d_k)}
\end{align}