Was ist eine Getriebestufe?

Als Getriebestufe bezeichnet man eine Radpaarung innerhalb eines Getriebes an dem sich die Drehzahl bzw. das Drehmoment ändert!

Definition

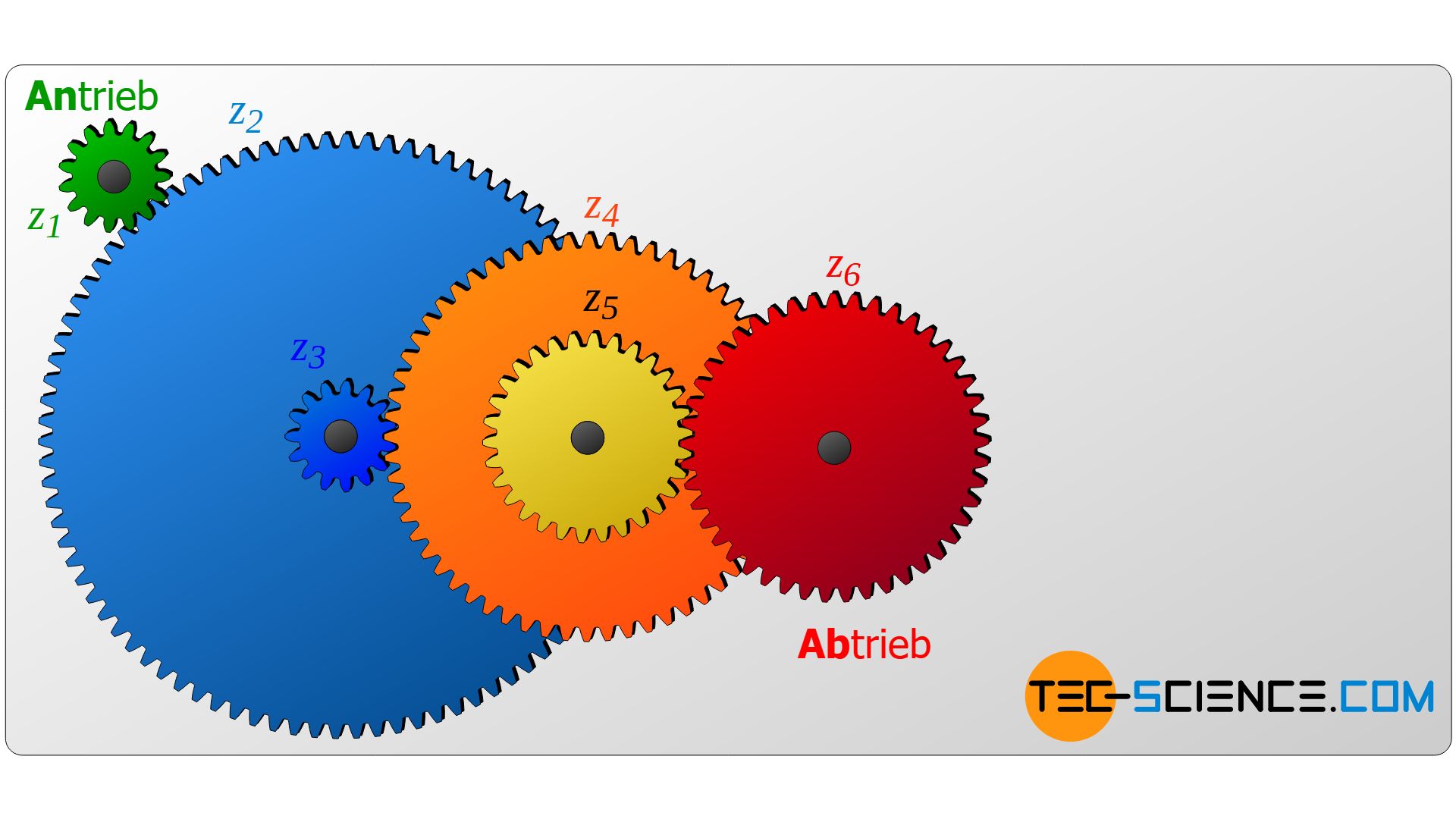
Die untere Abbildung zeigt schematisch ein Zahnradgetriebe, dessen grundsätzliche Funktion im Artikel Funktionsweise detaillierter erläutert wurde. Wie diese Animation deutlich macht, besteht ein Getriebe in der Regel nicht nur aus einem Zahnradpaar besteht sondern aus mehreren, die jeweils auf unterschiedlichen Wellen befestigt sind. Jedes Paar das dabei ineinander greift, stellt dabei eine sogenannte Getriebestufe dar.

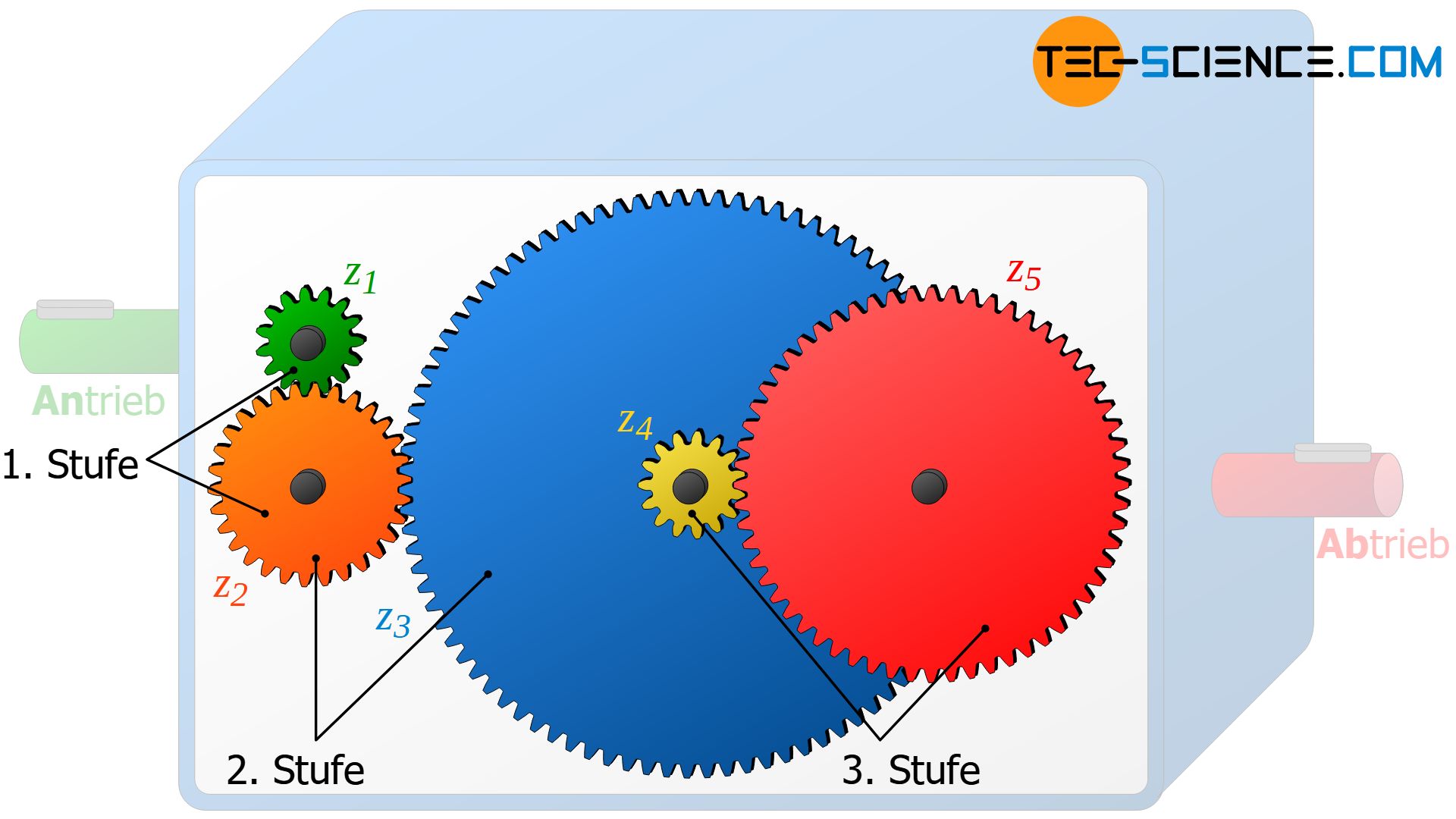
Eine Getriebestufe zeichnet sich dadurch aus, dass sich zwischen einem treibenden Rad und einem getriebenen Rad, die Drehzahl bzw. das Drehmoment ändert. Das oben abgebildete Getriebe besteht aus insgesamt drei Getriebestufen, wobei sich jeder Getriebestufe ein bestimmtes Übersetzungsverhältnis zuordnen lässt. Das Übersetzungsverhältnis ist dabei definiert als Verhältnis der Drehzahlen zwischen treibendem Rad (n_t) und getriebenem Rad (n_g):

\begin{align}
\label{def_uebersetzungsverhaeltnis}
&\boxed{i = \frac{n_t}{n_g}} \\[5px]
\end{align}

Als Getriebestufe bezeichnet man eine Radpaarung innerhalb eines Getriebes an dem sich die Drehzahl bzw. das Drehmoment ändert!

Die erste Getriebestufe bildet das grüne Zahnrad (z₁ = 15) und das orangefarbene Zahnrad (z₂ = 30). Die zweite Getriebestufe ergibt sich aus der Zahnradpaarung des orangefarbenen Zahnrades (z₂) und des blauen Zahnrades (z₃ = 90). Das grüne Zahnrad (z₄ = 15) und das rote Zahnrad (z₅ = 60) bilden schließlich die dritte Getriebestufe. Für die entsprechenden Getriebestufen ergibt sich hieraus folgende Übersetzungsverhältnisse i:

\begin{align}
\label{1}
&\text{1. Getriebestufe:}~~~ \underline{i_1} = \frac{n_t}{n_g} = \frac{z_2}{z_1} = \frac{30}{15} = \underline{2} \\[5px]
\label{2}
&\text{2. Getriebestufe:}~~~ \underline{i_2} = \frac{n_t}{n_g} = \frac{z_3}{z_2} = \frac{90}{30} = \underline{3} \\[5px]
\label{3}
&\text{3. Getriebestufe:}~~~ \underline{i_3} = \frac{n_t}{n_g} = \frac{z_5}{z_4} = \frac{60}{15} = \underline{4} \\[5px]
\end{align}

Beachte, dass es sich bei dem Zahnradpaar 3 und 4 nicht um eine Getriebestufe handelt, da sich die Zahnräder auf einer gemeinsamen Welle befinden. Die Drehzahl der beiden Zahnräder ist folglich identisch. Es findet somit weder eine Änderung der Drehzahl noch eine Änderung des Drehmomentes statt. Deshalb handelt es sich bei diesem Zahnradpaar auch nicht um eine Getriebestufe.

Gesamtübersetzungsverhältnis

Im selben Maße wie sich die Drehzahl gemäß den oben berechneten Übersetzungsverhältnissen von Stufe zu Stufe verringert, vergrößert sich das Drehmoment. So wird in der ersten Getriebestufe das Drehmoment der Getriebeeingangswelle verdoppelt. In der zweite Getriebestufe wird dieses verdoppelte Drehmoment nun nochmals verdreifacht. Folglich ist das Drehmoment nach der zweiten Stufe 6-mal so hoch wie an der Eingangswelle. Schließlich wird in der dritten Getriebestufe dieses 6-mal größere Drehmoment nun nochmals vervierfacht. Insgesamt hat man an der Ausgangswelle des Getriebes folglich das 24-fache an Drehmoment anliegen wie an der Getriebeeingangswelle!

Für die Drehzahlen gilt entsprechend der umgekehrte Zusammenhang. So wird die Drehzahl zwischen Eingang und Ausgang des Getriebes um das 24-fache verringert. Für eine Umdrehung der Getriebeausgangswelle muss sich die Eingangswelle folglich 24-mal drehen.

Vergleicht man also lediglich den Getriebeeingang und den Getriebeausgang, dann verhält sich das gesamte Getriebe wie eine einzelne Getriebestufe mit einem Übersetzungsverhältnis von 24. Dieses Übersetzungsverhältnis entspricht schließlich dem Gesamtübersetzungsverhältnis dem Übersetzungsverhältnis des Getriebes. Wie dieses Beispiel zeigt, lässt sich das Gesamtübersetzungsverhältnis i_ges eines Getriebes folglich aus der Multiplikation der einzelnen Übersetzungsverhältnisse der jeweiligen Getriebestufen ermitteln:

\begin{align}
\label{4}
&\boxed{i_{ges} = i_1 \cdot i_2 \cdot i_3 \cdot \dots}  \\[5px]
\end{align}

Das Gesamtübersetzungsverhältnis eines Getriebes ergibt sich aus der Multiplikation der Einzelübersetzungsverhältnisse der jeweiligen Getriebestufen!

Da das Übersetzungsverhältnis einer Getriebestufe vom Verhältnis der beteiligten Zähnezahlen abhängig ist, bedingt eine Änderung der Zähnezahl an einem der Zahnräder im Allgemeinen auch ein geändertes Gesamtübersetzungsverhältnis.

Wird bspw. das Zahnrad 5 (z₅ = 60 Zähne) durch ein doppelt so großes Zahnrad mit einer entsprechend doppelten Zähneanzahl ersetzt (z₅‚= 120 Zähne), so ergibt sich in dieser Getriebestufe nun auch ein doppelt so großes Übersetzungsverhältnis von i₃‚= 8. Mit dieser Verdoppelung wird auch das Gesamtübersetzungsverhältnis von ursprünglich 24 auf i_ges‚= 48 verdoppelt.

Beachte also, dass durch die Multiplikation der einzelnen Übersetzungsverhältnisse letztlich jede Getriebestufe direkt linear in das Gesamtübersetzungsverhältnis nach Gleichung (\ref{4}) eingeht. Die Verdopplung oder Verdreifachung einer einzelnen Getriebestufe bedeutet somit auch eine Verdopplung bzw. Verdreifachung des Gesamtübersetzungsverhältnisses.

Vorteile und Nachteile

Das im vorliegenden Beispiel erhaltene Gesamtübersetzungsverhältnis von 24 hätte man tatsächlich auch nur mit einer Getriebestufe erreichen können. Hierzu müsste allerdings das Zahnrad an der Abtriebswelle um das 24-fache so groß sein wie jenes an der Antriebswelle. Dementsprechend groß wären auch die Dimensionen des Getriebes.

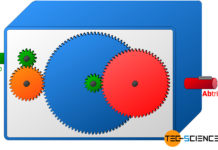
Die untere Abbildung zeigt im Vergleich zum vorgestellten 3-stufigen Getriebe die maßstabsgetreue Abmessung eines einstufigen Getriebes, das dasselbe Gesamtübersetzungsverhältnis aufweist.

Mehrstufige Getriebe bieten den Vorteil das gewünschte Übersetzungsverhältnis auf mehrere kleinere Zahnräder aufzuteilen und so die Abmessungen des Getriebes insgesamt klein zu halten.

Beachtet werden muss jedoch, dass sich mit jeder Getriebestufe auch die Reibungseinflüsse zunehmen. Zum einen dadurch, dass insgesamt mehr Zähne ineinander greifen, die im Allgemeinen aufeinander Abgleiten und damit auch mehr Reibung erzeugen. Und zum anderen dadurch, dass die jeweiligen Wellen der Getriebestufen gelagert werden müssen und somit eine erhöhte Lagerreibung verursachen.

Einfluss der Zähnezahlen

Es wurde bereits erläutert, dass die Änderung der Zähnezahl eines Zahnrades direkte Auswirkung auf das Übersetzungsverhältnis der entsprechenden Getriebestufe hat und im Allgemeinen somit auch das Gesamtübersetzungsverhältnis beeinflusst.

Im Falle des Zahnrades 2 wirkt sich eine Änderung der Zähnezahl allerdings nicht auf das Gesamtübersetzungsverhältnis aus! Dies wird sofort ersichtlich, wenn man sich die Formel zur Ermittlung des Gesamtübersetzungsverhältnisses einmal genauer anschaut. Hierzu werden die Formeln (\ref{1}) bis (\ref{3}) direkt in die Formel (\ref{4}) eingesetzt. Es zeigt sich dann, dass sich die Zähnezahl z₂ herauskürzt und somit das Gesamtübersetzungsverhältnis offensichtlich nicht hiervon abhängig ist:

\begin{align}
&\underline{i_{ges}} = i_1 \cdot i_2 \cdot i_3 = \frac{z_2}{z_1} \cdot \frac{z_3}{z_2} \cdot \frac{z_5}{z_4} = \underline{\frac{z_3 \cdot z_5}{z_1 \cdot z_4}}   \\[5px]
\end{align}

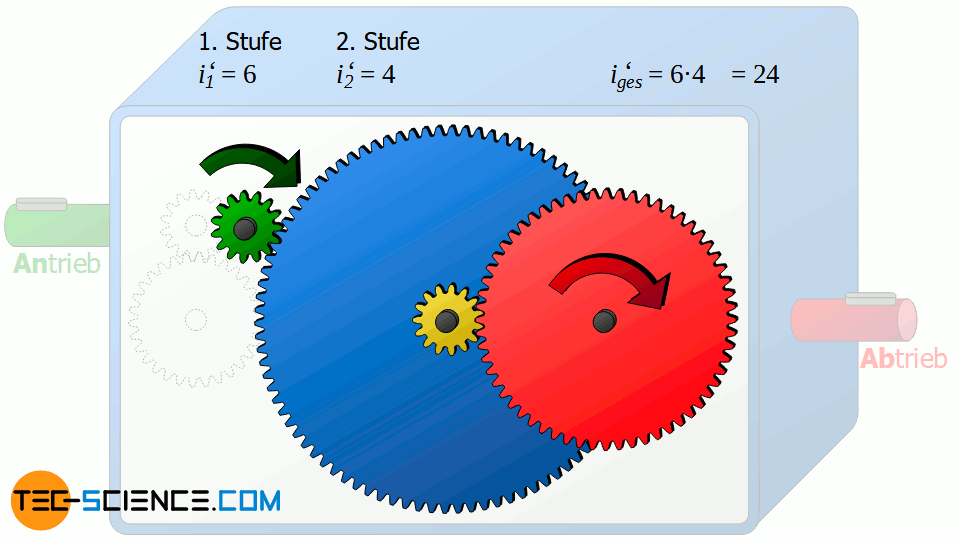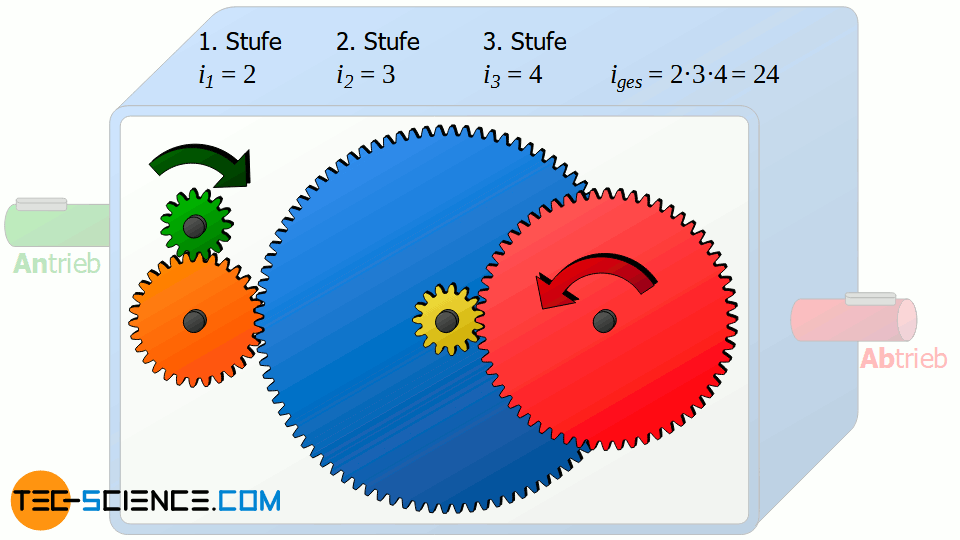
Wenn aber das Gesamtübersetzungsverhältnis nicht von diesem Zahnrad abhängig ist, welche Funktion erfüllt dies dann? Tatsächlich kann auf dieses Zahnrad 2 zunächst komplett verzichtet werden und damit das Zahnrad 1 direkt an das Zahnrad 3 gekoppelt werden, ohne dass sich dabei etwas am Gesamtübersetzungsverhältnis von 24 ändert! Eine Nachrechnung des nunmehr 2-stufigen-Getriebes liefert den Beweis:

\begin{align}
\text{1. Getriebestufe:}~~~ \underline{i_1} &= \frac{n_t}{n_g} = \frac{z_3}{z_1} = \frac{90}{15} = \underline{6} \\[5px]
\text{2. Getriebestufe:}~~~ \underline{i_2} &= \frac{n_t}{n_g} = \frac{z_5}{z_4} = \frac{60}{15} = \underline{4} \\[5px]
\text{Gesamtübersetzungsverhältnis:}~~~ \underline{i_{ges}} &= i_1 \cdot i_2 = 6 \cdot 4  = \underline{24} \\[5px]
\end{align}

Dass das Gesamtübersetzungsverhältnis unabhängig der Zähnezahl z₂ ist, kann auch anschaulich erklärt werden. Schiebt sich nämlich das Zahnrad 1 der Antriebswelle um einen Zahn weiter, so wird auch das Zahnrad 2 um einen Zahn weiterbewegt. Dieses Weiterbeweggen um einen Zahn wird nun vom Zahnrad 2 auf das Zahnrad 3 übertragen. Insofern dient das Zahnrad 2 lediglich als „Übermittler“ des Weiterschiebens. Somit kann eben auch das Zahnrad 1 direkt das Zahnrad 3 um einen Zahn weiterbewegen, ohne an dem prinzipiellen Vorgang etwas zu ändern.

Je nach Funktion des Getriebes ist jedoch das Zahnrad 2 keineswegs überflüssig. Denn ohne dieses rotiert die Abtriebswelle entgegen ihrem ursprünglichem Drehsinn! Das Zahnrad 2 dient somit als Zwischenrad und hat damit die Funktion den Drehsinn des Abtriebsrades entsprechend anzupassen (Drehrichtungsumkehr). Um diese Aufgabe zu erfüllen könnte das Zwischenrad 2 prinzipiell auch zwischen Zahnrad 4 und 5 geschaltet werden.

Ein Zwischenrad dient der Drehrichtungsumkehr, ohne dabei das Gesamtübersetzungsverhältnis zu beeinflussen!

Anordnung der Zahnräder

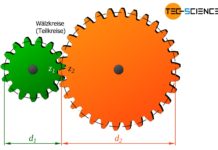
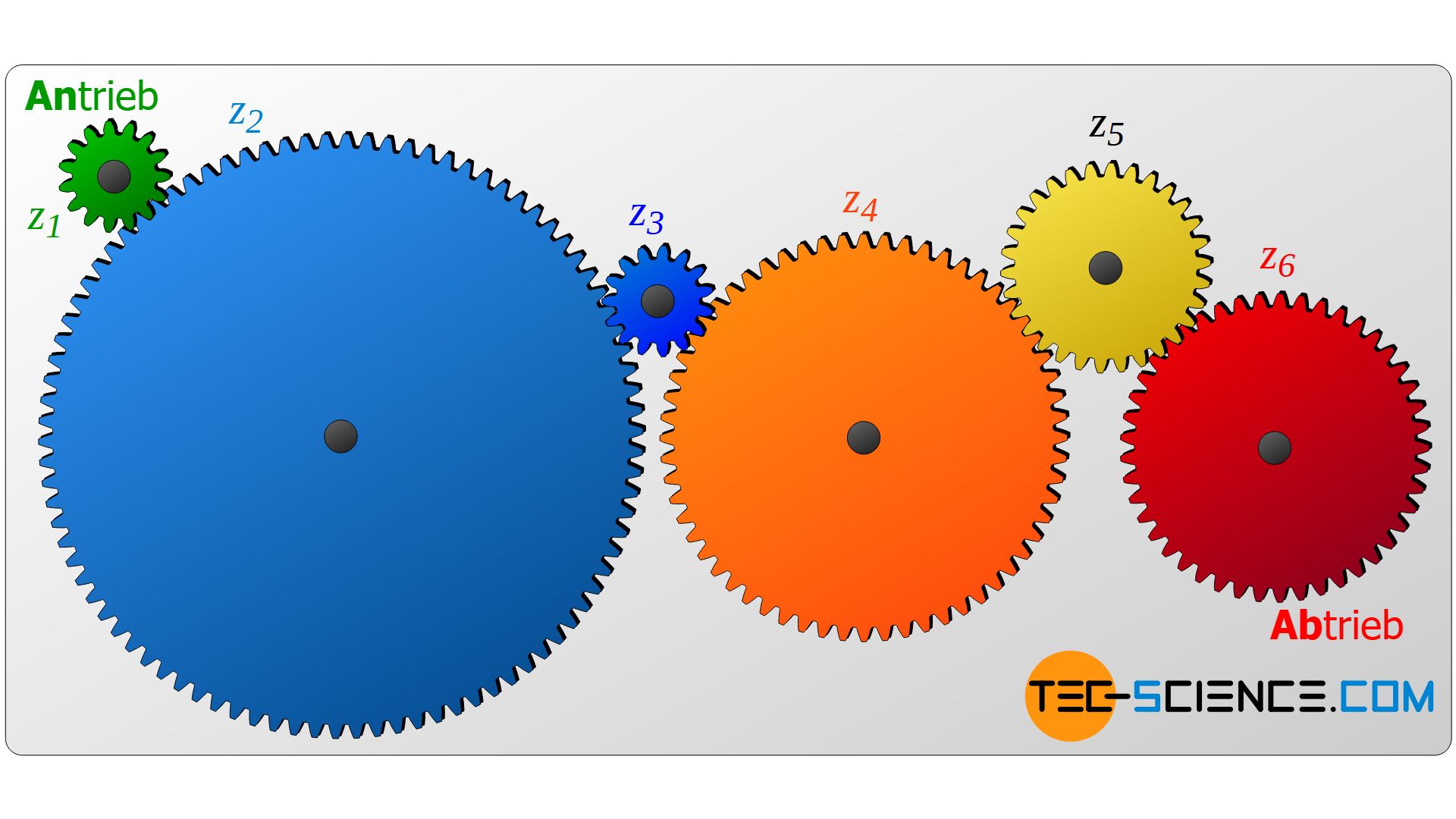
Unter welchen Umständen hat nun die Zähnezahl eines Zahnrades Einfluss auf das Gesamtübersetzungsverhältniss und wann nicht? Die untere Abbildung zeigt hierzu Zahnräder die sich jeweils auf getrennten Wellen befinden. In einem solchen Fall ist das Gesamtübersetzungsverhältnis nur von der Zähnezahl des ersten (z₁) und des letzten Zahnrades (z₆) abhängig:

\begin{align}
\require{cancel}
&\underline{i_{ges}} = i_1 \cdot i_2 \cdot i_3 \cdot i_4 \cdot i_5 = \frac{\bcancel{z_2}}{z_1} \cdot \frac{\bcancel{z_3}}{\bcancel{z_2}} \cdot \frac{\bcancel{z_4}}{\bcancel{z_3}} \cdot \frac{\bcancel{z_5}}{\bcancel{z_4}} \cdot \frac{z_6}{\bcancel{z_5}} = \underline{\frac{z_6}{z_1}} \\[5px]
\end{align}

Um Zahnradgetriebe also effektiv gestalten zu können, müssen stets zwei unterschiedliche Zahnräder auf einer gemeinsamen Welle angeordnet werden, die ihrerseits wieder eine Welle mit Zahnradpaar antreibt. In diesem Fall gehen dann die gesamten Zähnezahlen aller Zahnräder in die Berechnung des Gesamtübersetzungsverhältnisses ein!

\begin{align}
\require{cancel}
&\underline{i_{ges}} = i_1 \cdot i_2 \cdot i_3 = \underline{ \frac{z_2}{z_1} \cdot \frac{z_4}{z_3} \cdot \frac{z_6}{z_5}} \\[5px]
\end{align}