Experimentelle Bestimmung der Viskosität (Viskosimetrie)

Als Viskosimetrie bezeichnet man die experimentelle Bestimmung der Viskosität (Zähigkeit) von Flüssigkeiten und Gasen.

Definition der Viskosität (Newtonsches Reibungsgesetz)

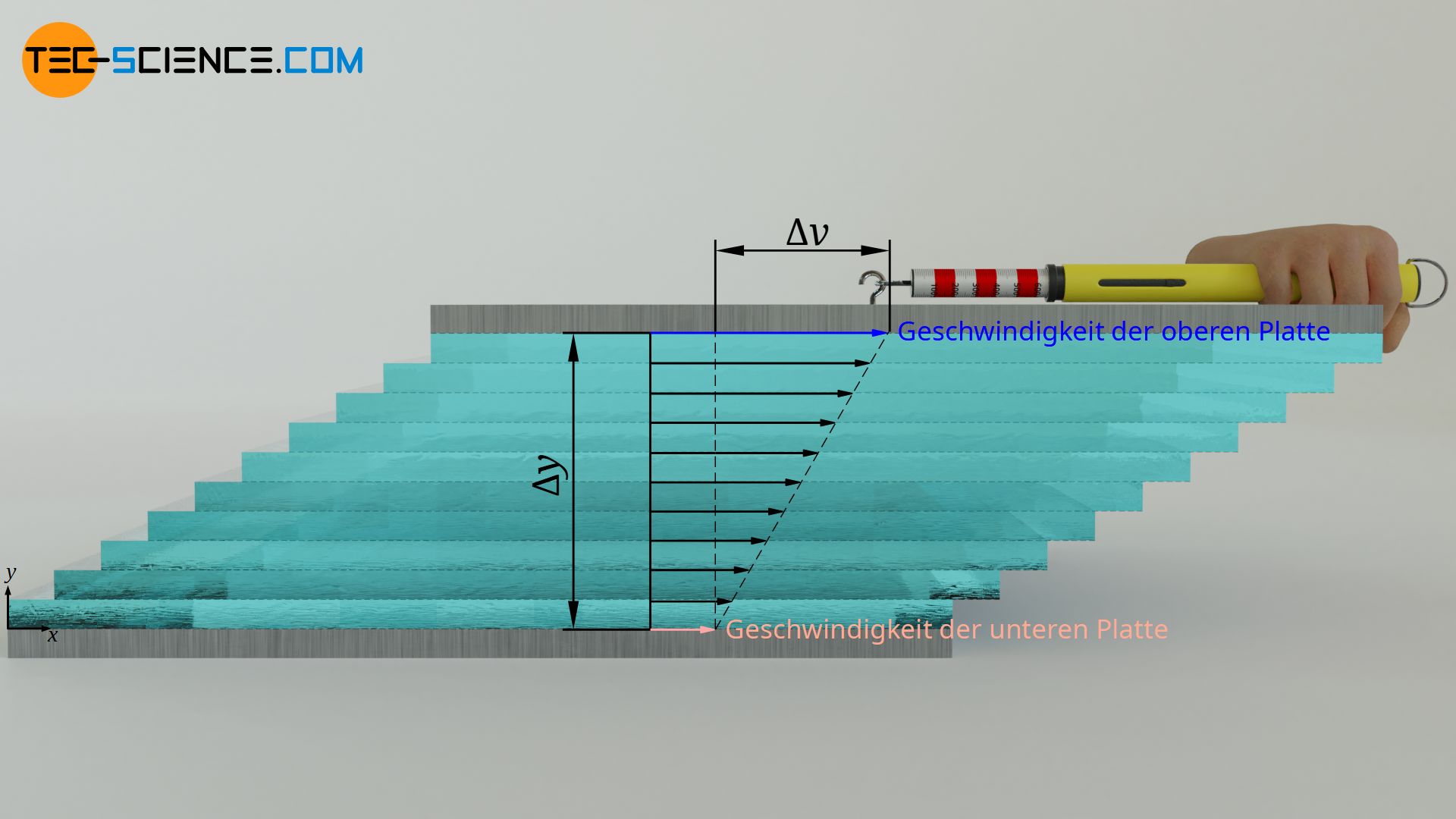
Die Viskosität beschreibt den inneren Fließwiderstand eines Fluids. Sie ist über die Schubspannung τ definiert, die benötigt wird, um zwei relativ zueinander bewegter Platten zu verschieben. Die Schubspannung ist umso größer je höher die Relativgeschwindigkeit Δv der Platten und je geringer der Plattenabstand Δy. Der Proportionalitätsfaktor zwischen diesen Größen entspricht der (dynamischen) Viskosität η. Diese Gesetzmäßigkeit wird auch als Newtonsches Reibungsgesetz bezeichnet:

\begin{align}
\label{t}
&\boxed{\tau= \eta \cdot \frac{\Delta v}{\Delta y}} ~~~&&\text{Newtonsches Reibungsgesetz}\\[5px]
&{\tau=\frac{F}{A}} ~~~&&\text{ Scherspannung} \\[5px]
\end{align}

Ausführlichere Informationen zur Viskosität und zum Newtonschen Reibungsgesetz finden Sie im Artikel Viskosität.

Rotations-Viskosimeter

Das Einschließen eines Fluids zwischen zwei Platten zur Definition der Viskosität ist zwar eine sehr anschauliche Vorgehensweise, jedoch ist in der Praxis kaum umsetzbar. Wie sollte bspw. das Fluid innerhalb des Spaltes zweier Platten gehalten werden? Man benutzt in der Praxis deshalb eine Spindel die mit konstanter Drehzahl in einem zylindrischen Gefäß rotiert. Im Gefäß befindet sich dann die Flüssigkeit, deren Viskosität bestimmt werden soll. Eine solche Apparatur zur Bestimmung der Viskosität wird auch als Rotations-Viskosimeter bezeichnet.

Je nach Viskosität erfordert der Antrieb der Spindel ein bestimmtes Drehmoment. Je höher die Viskosität, desto größer das benötigte Drehmoment um, die Drehzahl konstant zu halten. Dieses Drehmoment wird direkt am Motor bestimmt und kann nach einer entsprechenden Kalibrierung zur Bestimmung der Viskosität genutzt werden. Zu hoch darf die Drehzahl allerdings nicht gewählt werden, da sich bei zu hohen Geschwindigkeiten keine laminare Strömung mehr ausbildet (Schichtenströmung), sondern eine turbulente Strömung (Wirbelströmung).

Kugelfall-Viskosimeter

Die Viskosität eines Fluids kann man auch durch Fallversuche ermitteln. Die Geschwindigkeit, mit der eine Kugel in einem Fluid zu Boden fällt, hängt nämlich direkt von der Viskosität des Fluids ab. Als Fluide werden dabei hauptsächlich Flüssigkeiten verwendet.

Der Physiker George Gabriel Stokes ermittelte folgende Gleichung, die den Zusammenhang wiedergibt zwischen der Geschwindigkeit v, mit der eine Kugel mit dem Radius r durch ein Fluid der Viskosität η gezogen wird und der hieraus resultierenden Reibungskraft F_R:

\begin{align}
\label{s}
&\boxed{F_R = 6\pi \cdot r \cdot \eta \cdot v} ~~~\text{Stoke’sches Reibungsgesetz} \\[5px]
\end{align}

Beachte, dass das Gesetz von Stoke nur für sphärische Körper gilt, die laminar umströmt werden!

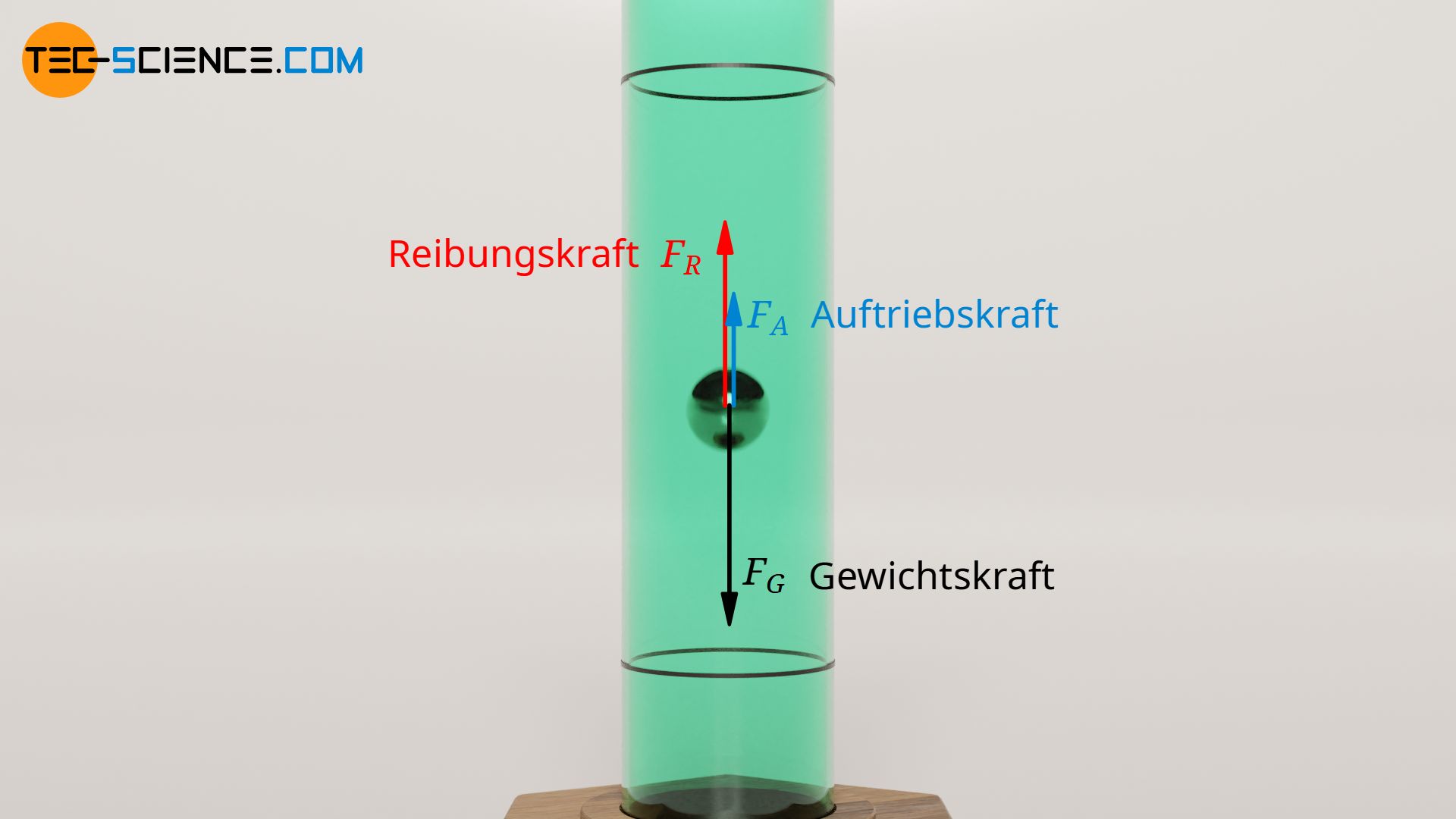
Lässt man eine Kugel in einer viskosen Flüssigkeit fallen, dann steigt die Geschwindigkeit zunächst solange an, bis die entgegenwirkende Reibungskraft genauso groß ist wie die nach unten wirkende Gewichtskraft der Kugel. Für genauere Messungen muss zudem noch die nach oben gerichtete Auftriebskraft berücksichtigt werden. Alle drei Kräfte bilden im stationären Fall einen Gleichgewichtszustand und man erhält eine konstante Sinkgeschwindigkeit:

\begin{align}
\label{gg}
&F_G \overset{!}{=} F_R + F_A \\[5px]
\end{align}

Die Gewichtskraft F_G der Kugel kann über das Volumen V_K und die Dichte der Kugel ϱ_K ermittelt werden:

\begin{align}
\label{g}
&F_G = m_K \cdot g = V_K \cdot \rho_K \cdot g= \frac{4}{3}\pi r^3 \cdot \rho_K \cdot g\\[5px]
\end{align}

Die Auftriebskraft F_A bestimmt gemäß des Archimedischen Prinzips aus der Gewichtskraft der verdrängten Flüssigkeit, wobei das verdrängte Volumen gerade dem Volumen der Kugel entspricht:

\begin{align}
\label{a}
&F_A = m_F \cdot g = V_K \cdot \rho_F \cdot g= \frac{4}{3}\pi r^3 \cdot \rho_F \cdot g \\[5px]
\end{align}

Setzt man nun die Gleichungen (\ref{s}), (\ref{g}) und (\ref{a}) in Gleichung (\ref{gg}) ein, dann lässt sich die Viskosität η der Flüssigkeit wie folgt anhand deren Sinkgeschwindigkeit v_s ermitteln:

\begin{align}
&F_G \overset{!}{=} F_R + F_A \\[5px]
&\frac{4}{3}\pi r^3 \cdot \rho_K \cdot g = 6\pi \cdot r \cdot \eta \cdot v_\text{s} + \frac{4}{3}\pi r^3 \cdot \rho_F \cdot g \\[5px]
&6\pi \cdot r \cdot \eta \cdot v_\text{s} = \frac{4}{3}\pi r^3 \cdot \rho_K \cdot g ~- \frac{4}{3}\pi r^3 \cdot \rho_F \cdot g \\[5px]
&6\pi \cdot r \cdot \eta \cdot v_\text{s} = \frac{4}{3}\pi r^3 g \left(\rho_K-\rho_F\right) \\[5px]
\label{e}
&\boxed{\eta = \frac{2r^2g}{9~ v_\text{s}}\left(\rho_K-\rho_F\right) } ~~~~~r \ll R\\[5px]
\end{align}

Bei der Durchführung des Experiments, darf die Sinkgeschwindigkeit allerdings nicht zu hoch sein. Zum einen, weil dann nicht sichergestellt werden kann, dass ein Gleichgewichtszustand erreicht worden ist, bevor die Kugel wieder auf den Boden aufkommt. Zum anderen muss stets eine laminare Strömung um die Kugel herum gewährleistet sein, was bei hohen Geschwindigkeiten nicht der Fall ist, da dann Verwirbelungen entstehen.

Zudem sollte der Radius R des zylindrischen Fallrohrs im Vergleich zum Radius r darin fallenden Kugel ausreichend groß sein, da es ansonsten zu nicht mehr zu vernachlässigenden Strömungseffekten zwischen Kugel und Gefäßwand kommt. Die Folge ist eine zusätzliche Reibung der vorbeiströmenden Flüssigkeit und eine Verringerung der Sinkgeschwindigkeit der Kugel (Prinzip der hydraulischen Dämpfung).

Aufgrund der endlichen Ausdehnung des Fallrohrs wird die Sinkgeschwindigkeit der Kugel in der Praxis also stets zu klein gemessen, um mit ihr die Viskosität nach Gleichung (\ref{e}) bestimmen zu können. Man korrigiert deshalb die Sinkgeschwindigkeit nach Ladenburg mit einem empirischen Korrekturfaktor C nach oben, um damit auf die Sinkgeschwindigkeit für den Fall eines unendlich ausgedehnten Fallrohres zu kommen:

\begin{align}
\label{h}
&\boxed{\eta = \frac{2r^2g}{9 ~v_\text{s} \cdot C}\left(\rho_K-\rho_F\right) } ~~~\text{mit}~~~ \boxed{C=1+2,1 \frac{r}{R}}>1 \\[5px]
\end{align}

Der Korrekturfaktor wird in der Praxis meist im Vorfeld des Versuchs mit Hilf einer Flüssigkeit mit bekannter Viskosität bestimmt.

Kugelfall-Viskosimeter nach Höppler

Das Kugelfall-Viskosimeter nach Höppler beruht auf der im Abschnitt zuvor beschriebenen Kugelfall-Methode. Eine Kugel fällt in einem Fallrohr zu Boden, die die zu untersuchende Flüssigkeit enthält. Am Fallrohr sind zwei Markierungen angebracht, die eine definierte Messstrecke Δs („Fallstrecke“) vorgeben. Die Zeitdauer Δt, die die Kugel benötigt um diese Messstrecke zu durchlaufen, wird mit Hilfe von Lichtschranken gemessen. Für die Sinkgeschwindigkeit v_s der Kugel gilt damit:

\begin{align}
& v_\text{s} = \frac{\Delta s}{\Delta t}\\[5px]
\end{align}

Wird die Formel für die Sinkgeschwindigkeit in Gleichung (\ref{h}) eingesetzt, dann lässt sie wie folgt auf die Viskosität η der Flüssigkeit schließen:

\begin{align}
&\eta = \underbrace{\color{red}{\frac{2r^2g}{9 \cdot \Delta s \cdot C}}}_{\text{Konstante}~ \color{red}{K}} \cdot \left(\rho_K-\rho_F\right) \cdot \Delta t\\[5px]
\label{eta}
&\boxed{\eta = K \cdot \left(\rho_K-\rho_F\right) \cdot \Delta t } \\[5px]\\[5px]
\end{align}

Der rot markierte Term ist eine spezifische Konstante der Messaparatur, die auch von der verwendeten Prüfkugel abhängig ist. Je nach zu erwartender Viskosität stellen die Hersteller von Höppler-Viskosimetern verschiedene Kugel zur Verfügung, für die die Prüfkonstante C im Vorfeld ermittelt worden ist.

In dieser Konstante ist ebenfalls berücksichtigt, dass das Fallrohr nicht exakt senkrecht ausgerichtet ist, sondern etwas schräg gestellt ist. Die Kugel führt deshalb auch keine rein fallende Bewegung aus, sondern ebenfalls eine leicht rollende Bewegung. Die Kugel wird durch diese leicht rollende Bewegung auf stabilem Wege nach unten geführt. Auf diese Weise werden Turbulenzen in der Flüssigkeit vermieden und die qualitative Gültigkeit des Stoke’schen Gesetzes sichergestellt, d.h. insbesondere die Proportionalität zwischen Reibungskraft und Sinkgeschwindigkeit. Bei turbulenter Umströmung wäre die Reibungskraft nicht mehr proportional zur Sinkgeschwindigkeit und die Viskosität keine lineare Funktion der Falldauer. Gleichung (\ref{eta}) wäre nicht mehr gültig.

Um den Temperatureinfluss auf die Viskosität zu untersuchen, befindet sich das Fallrohr meist in einem weiteren Rohr, das mit Wasser gefüllt ist. Durch Umwälzthermostate kann das Wasserbad und somit die zu untersuchende Flüssigkeit präzise temperiert werden.

Kapillar-Viskosimeter nach Ubbelohde

Das Kapillarviskosimeter beruht auf dem Hagen-Poiseuille-Gesetz für Rohrströmungen. Dieses besagt, dass der Volumenstrom V* durch eine Kapillare bei vollständig ausgebildeter Strömung wie folgt von der Viskosität η der durchströmenden Flüssigkeit abhängig ist:

\begin{align}
&\boxed{\dot V = – \frac{\pi R^4}{8 l \eta}\Delta p } \\[5px]
\end{align}

Darin bezeichnet R den Radius der Kapillare und l die Länge. Die Druckdifferenz Δp entspricht dem Druckunterschied zwischen Anfang und Ende der Kapillare, die letztlich das Strömen der Flüssigkeit verursacht. Unterhalb der Kapillare ist ein L-förmiges Rohr angebracht, sodass oberhalb und unterhalb der Kapillare derselbe äußere Umgebungsdruck herrscht. Somit wird die Flüssigkeit angetrieben vom hydrostatischen Druck durch die Kapillare bewegt. Die Druckdifferenz Δp ist also abhängig von der Dichte der Flüssigkeit.

Der Volumenstrom durch die Kapillare kann durch eine Zeitmessung und die Ermittlung der innerhalb dieser Zeit hindurchgeströmten Masse ermittelt werden. Jedoch fassen Hersteller von Kapillar-Viskosimetern die geräteabhängigen Größen wie Radius und Länge der Kapillare meist in einer Konstanten K zusammen. Somit muss lediglich die Zeitdauer t bestimmt werden, innerhalb deren die Flüssigkeit im Reservoir zwei Markierungen passiert hat. Zudem ist die Dichte der Flüssigkeit ϱ_F erforderlich, da diese die Druckdifferenz im Hagen-Poiseuille-Gesetz bestimmt. Mit folgender Formel lässt sich die Viskosität η dann ermitteln:

\begin{align}
&\boxed{\eta= K \cdot \rho_F \cdot (t-t_K)} \\[5px]
\end{align}

Wie bereits angedeutet, gilt das Hagen-Poiseuille-Gesetz nur für eine vollständig ausgebildete Strömung. Beim Übergang vom Reservoir zur Kapillare (und bis zu einem gewissen Grad auch innerhalb) ist die Strömung aber noch nicht vollständig ausgebildet, sondern sie wird beschleunigt. Der damit verbundene Energieaufwand bedeutet einen zusätzlichen Druckverlust. Um dies zu berücksichtigen wird die gemessene Zeit deshalb um eine Hagenbachsche Korrekturzeit t_K korrigiert.

Auslauf-Viskosimeter

Eine sehr simple Methode zur Bestimmung der Viskosität ist das Auslauf-Viskosimeter. Dabei macht man sich zu Nutze, dass das Ausströmen einer Flüssigkeit durch ein Loch in einem Gefäß ebenfalls von der Viskosität abhängig ist. Hoch viskose Flüssigkeiten benötigen aufgrund des hohen Fließwiderstandes relativ lange, bis sie durch ein Loch in dem Tauchbecher ausgeflossen sind. Für ein fest vorgegebenes Bechervolumen ist die Auslaufdauer deshalb ein direktes Maß für die Viskosität der Flüssigkeit.

Hersteller von Tauchbechern geben in ihren Datenblättern je nach Auslaufdauer die entsprechende Viskosität an. Je nach zu erwartender Viskosität sind unterschiedliche Tauchbecher zu verwenden. Um valide Ergebnisse zu erhalten, muss die Auslaufdauer zudem innerhalb eines bestimmten Bereichs liegen. Ist dies nicht gegeben, so muss ein anderer Tauchbecher benutzt werden.

Das Auslauf-Viskosimter wird hauptsächlich zur Bestimmung der Viskosität von Lacken und Farben verwenden. Diese Flüssigkeiten würden konventionelle Viskosimeter ansonsten stark verunreinigen. Zudem erhält man mit einem Auslaufviskosimeter sehr schnelle Ergebnisse, sodass Farben und Lacke nach dem Mischen unmittelbar kontrolliert und weiterverarbeitet werden können.