Der Dauerschwingversuch nach Wöhler gibt Aufschluss über die Festigkeit eines Werkstoffes bei stetig wechselnder Beanspruchung (dynamische Belastung).
Einleitung
Die Stärke der Beanspruchung nimmt im Zugversuch, Druckversuch und Biegeversuch langsam aber stetig zu, bis es schließlich zum Gewaltbruch kommt. Vor allem bei statisch belasteten Bauteilen liefern die hieraus ermittelten Festigkeitskenngrößen brauchbare Werte für die Werkstoffauswahl und Bauteildimensionierung.
In den meisten Fällen unterliegen Bauteile jedoch dynamischen Belastungen. Bei solchen wechselnden Belastungen ändert sich nicht nur die Beanspruchungsstärke stetig, sondern auch die Beanspruchungsrichtung wechselt permanent. Antriebswellen, Zahnräder, Kettenglieder, Federn, Pleuelstangen und Zylinderkopfschrauben sind nur einige Beispiele hierfür.
Die Praxis zeigt, dass Bauteile die einer ständig wechselnden Beanspruchung unterliegen auf Dauer nur geringere Spannungswerte ertragen als bei statischer Beanspruchung. Selbst wenn die Spannung dabei stets unterhalb der Streckgrenze des Werkstoffes bleibt, kann es mit der Zeit dennoch zum sogenannten Ermüdungsbruch kommen. Diese wird auch als Dauerbruch oder Schwingbruch bezeichnet. Um auch dieses Verhalten von Werkstoffen und ganzen Bauteilen bei dynamisch wechselnder Beanspruchung („Schwingung“) zu prüfen, nutzt man deshalb den Dauerschwingversuch nach Wöhler.
Die einzuhaltenden Beanspruchungsgrenzen sind bei dynamischer Belastung geringer als bei statischer Belastung!
Versuchsaufbau
Im Dauerschwingversuch setzt man nicht nur genormte Proben, sondern auch ganze Bauteile einer Schwingbeanspruchung aus. Hierzu wird die Probe in eine Vorrichtung gespannt, ähnlich einer Zugmaschine. Während die untere Einspannvorrichtung statisch mit der Umgebung verbunden ist, wird die obere Einspannung per Resonanz dynamisch in Schwingung versetzt. Auf diese Weise wird die Probe im einfachsten Fall abwechselnd auf Zug- und Druck beansprucht (Wechselbereich).
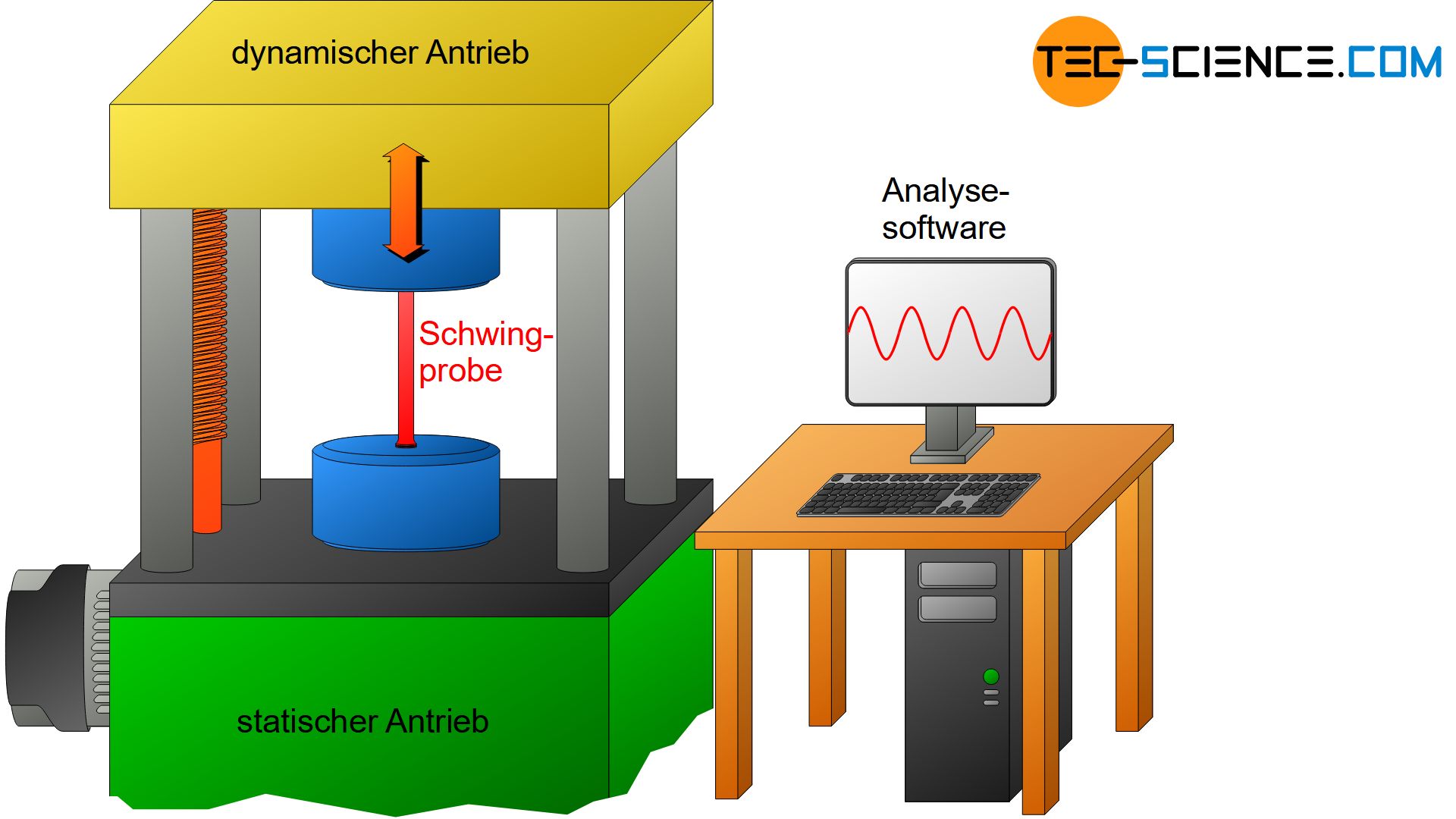
Bei der periodischen Beanspruchung handelt es sich antriebsbedingt um sinusförmige Schwingungen. Die Frequenzen hierfür liegen teilweise über 200 Hz. Höhere Frequenzen verringern zwar die Prüfzeit, jedoch darf es dabei nicht zu einer unzulässig hohen Erwärmung der Probe kommen.
Der statische Teil der Prüfmaschine ist zusätzlich mit einem Linearantrieb versehen. Auf diese Weise lässt sich der Tisch im Vorfeld des Versuchs absenken oder anheben. Hierdurch kann eine Vorbeanspruchung auf die eingespannte Probe aufgebracht werden. Die Spannung schwingt dann im Dauerschwingversuch um diese zuvor aufgebrachte Mittelspannung. Hierdurch wird erreicht, dass die Schwingbeanspruchung bspw. vollständig im Zug- oder im Druckbereich stattfindet. Man spricht in einem solchen Fall nicht mehr vom Wechselbereich, sondern vom Zugschwellbereich bzw. Druckschwellbereich. Auch in diesen Lastbereichen können je nach Anwendungsfall Dauerschwingversuche durchgeführt werden.
Grundbegriffe
Ein vollständiges Durchlaufen der unterschiedlichen Spannungszustände, wird als Schwingspiel oder Lastspiel bezeichnet. Die Gesamtzahl der durchlaufenen Schwingungszyklen bis zu einem bestimmten Zeitpunkt wird dann Schwingspielzahl oder Lastspielzahl \(N\) genannt. Dementsprechend bezeichnet die Bruchschwingspielzahl bzw. Bruchlastspielzahl \(N_B\) die Anzahl an Lastwechsel bis zu einem möglichen Bruch der Probe.
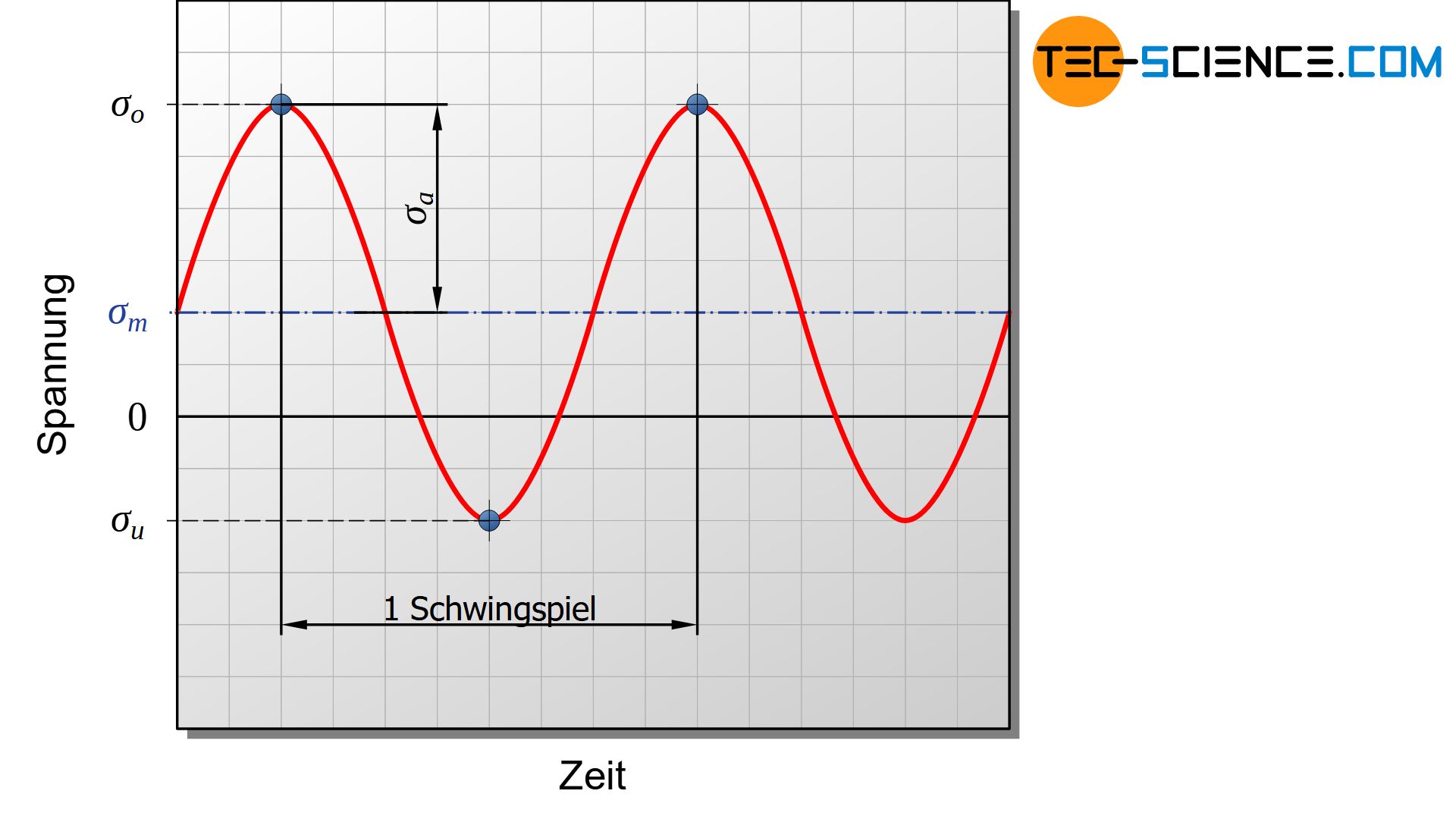
Als Lastspiel oder Schwingspiel bezeichnet an das einmalige Durchlaufen eines Spannungszykluses, bis dieser wieder von vorne beginnt!
Die maximale Spannung die die Probe erfährt, wird als Oberspannung \(\sigma_o\) bezeichnet. Folglich bezeichnet man als Unterspannung \(\sigma_u\) die minimal auftretende Spannung. Die Mittelspannung \(\sigma_m\) ergibt sich folglich aus dem Mittelwert dieser Grenzspannungen. Der Spannungsausschlag ausgehend der Mittelspannung hin zur Ober- bzw. Unterspannung entspricht der Spannungsamplitude \(\sigma_a\). Das Verhältnis von Unter- zur Oberspannung wird als Spannungsverhältnis \(R\) bezeichnet.
\begin{align}
\label{spannungsverhaeltnis}
&\boxed{R = \frac{\sigma_u}{\sigma_o}} ~~~~~\text{Spannungsverhältnis} \\[5px]
\end{align}
Bei Wechselbeanspruchung ist das Spannungsverhältnis negativ, da sich Oberspannung und Unterspannung durch ihre Vorzeichen unterscheiden. Eine reine Wechselbeanspruchung liegt bei einem Spannungsverhältnis von \(R\) = -1 vor (Lastfall III). Spannungsverhältnisse größer Null vollziehen sich ohne Vorzeichenwechsel, sodass dann eine Schwellbeanspruchung vorliegt. Für den Fall \(R\) = 0 herrscht eine reine Schwellbeanspruchung (Lastfall II). Bei einem Spannungsverhältnis von \(R\) = 1 sind Ober- und Unterspannung identisch, sodass dies letztlich dem Grenzfall der statischen Beanspruchung entspricht (Lastfall I).
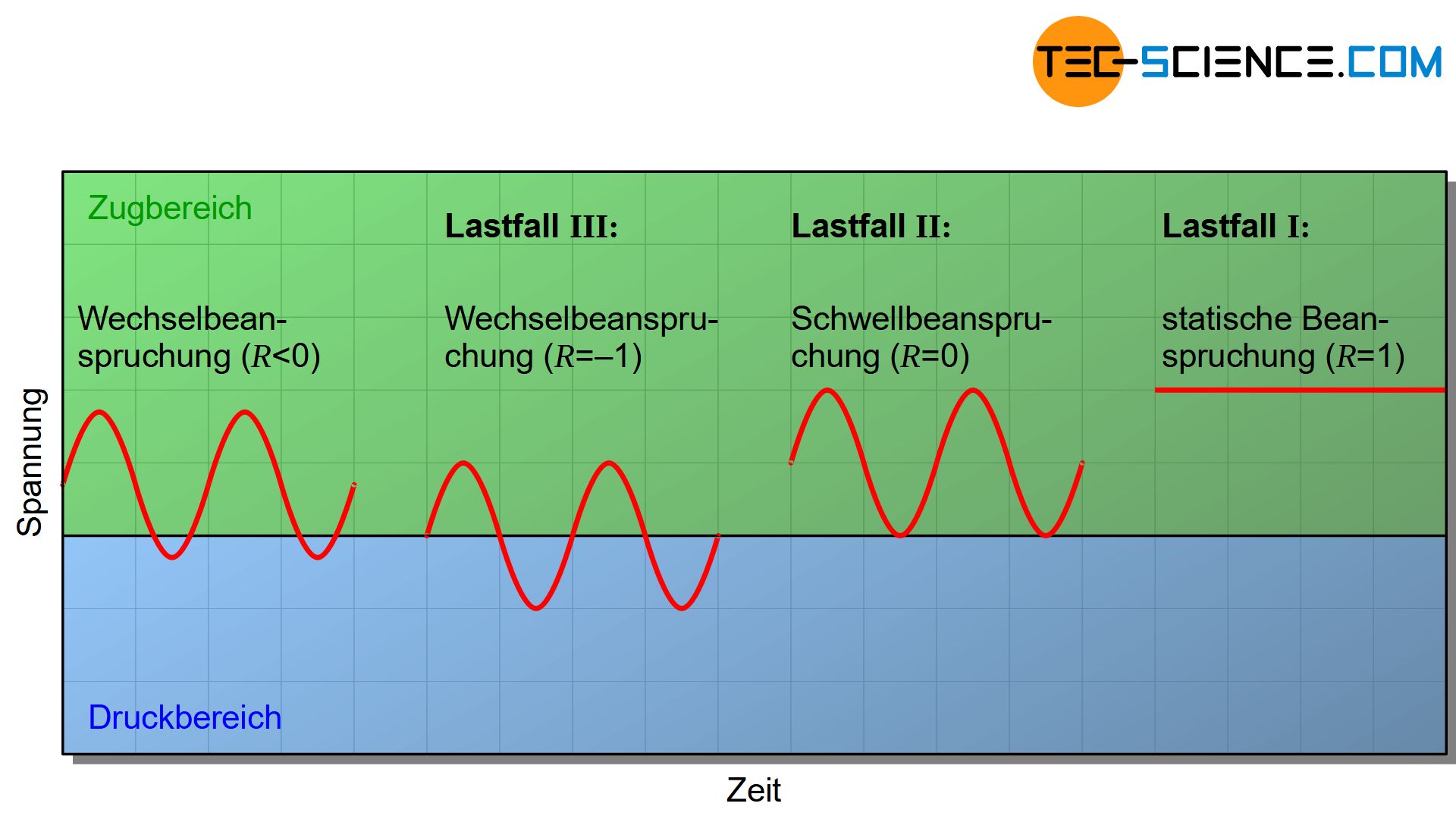
Bei einer Wechselbeanspruchung ändert sich nicht nur der Betrag der Beanspruchungsstärke, sondern auch die Beanspruchungsrichtung. Bei einer Schwellbeanspruchung variiert hingegen nur die Beanspruchungsstärke unter Beibehaltung der Beanspruchungsrichtung!
Wöhler-Diagramm
Um die Schwingfestigkeit von Materialien mit dem Wöhlerversuch nun zu untersuchen, stellt man im Vorfeld mehrere identische Proben eines Werkstoffes her. Anschließend werden die Proben nacheinander geprüft. Hierzu wird bei konstanter Mittelspannung \(\sigma_m\) und bei ebenfalls konstanter Spannungsamplitude \(\sigma_a\) die Anzahl an Schwingungen bis zum Bruch der Probe ermittelt. Diese Vorgehensweise wiederholt man an den weiteren Proben. Dabei wird bei allen Versuchen einer Versuchsreihe die Mittelspannung nicht geändert. Lediglich die Spannungsamplitude variiert von Probe zu Probe. Dabei wird die Spannungsamplitude in der Regel immer kleiner gewählt. Schließlich wird bei ausreichend kleiner Spannungsamplitude kein Bruch mehr eintreten. Die Probe wird folglich als dauerfest bezeichnet.
Im Dauerschwingversuch nach Wöhler werden mehrere identische Proben mit unterschiedlichen Spannungsamplituden dynamisch belastet und die jeweilige Bruchlastspielzahl ermittelt!
Wird für jede geprüfte Probe die jeweilige Spannungsamplitude \(\sigma_a\) über der entsprechend erreichten Bruchlastspielzahl \(N_B\) aufgetragen, so erhält man das sogenannte Wöhler-Diagramm. Aufgrund der extremen Spannweite der Bruchlastspiele wählt man auf der horizontalen Achse eine logarithmische Einteilung.
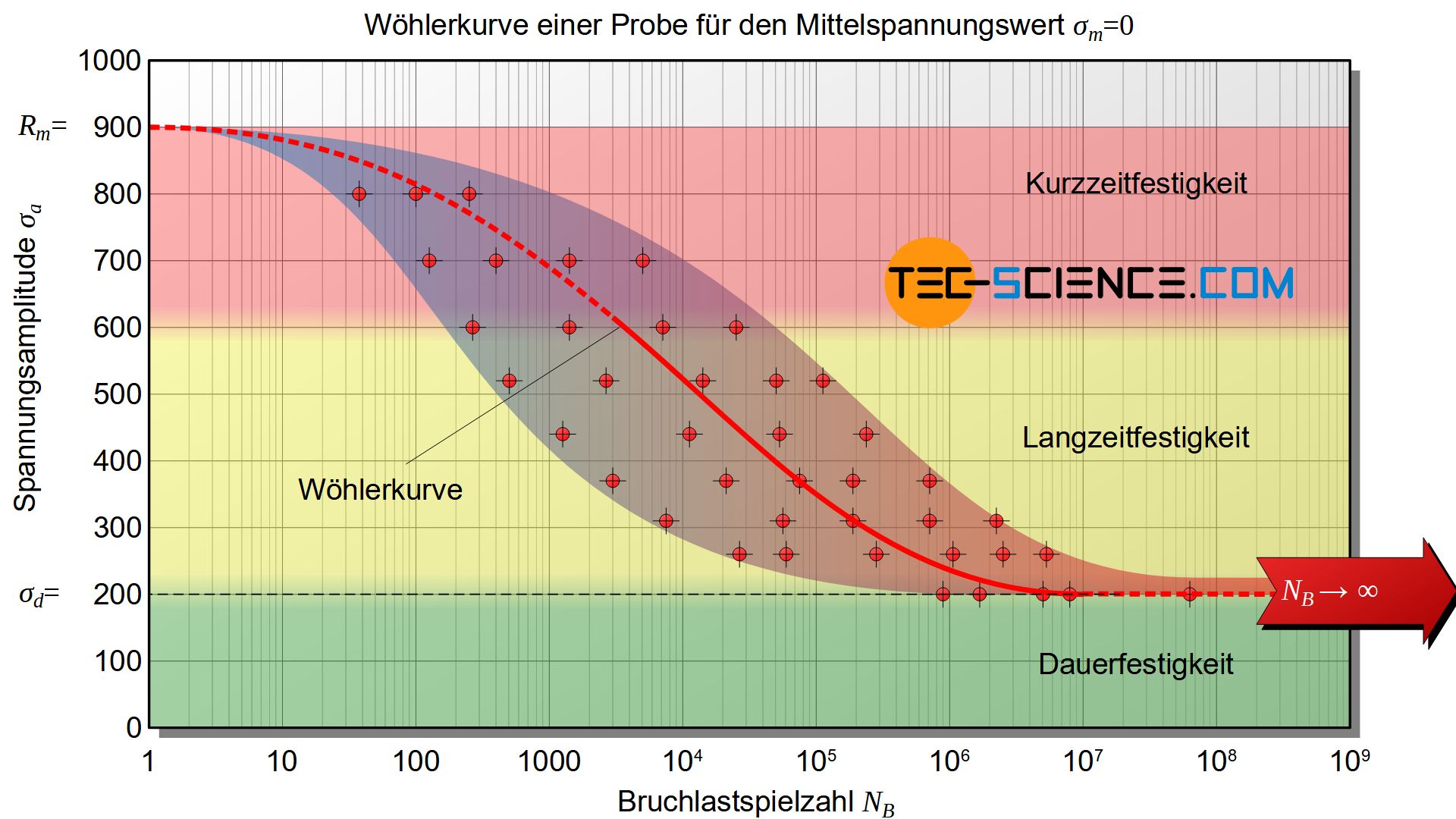
Die sich im Diagramm ergebende Kurve wird als Wöhler-Kurve bezeichnet. Eine solche Wöhlerkurve ergibt sich nach statistischer Auswertung von mehreren Proben, welche mit identischer Spannungsamplitude geprüft wurden. Eine solche statistische Auswertung ist deshalb nötig, da selbst bei identischer Spannungsamplitude sehr starke Streuungen in der Bruchlastspielzahl auftreten. Die starke Streuung ist eine Folge von fertigungsbedingten Gefügeunterschieden in der Probenherstellung. Solche Unterschiede lassen sich letztlich nie ganz vermeiden. Auf diese Weise könnten bereits geringe Unsauberkeiten in der Probenoberfläche zu einer verfrühten Rissbildung führen. In der Folge bricht die Probe vorzeitig. Insofern ist die Wöhlerkurve als Wahrscheinlichkeitskurve zu interpretieren, bei der bspw. 50 % der Proben die jeweilige Bruchlastspielzahl erreichen.
Als Wöhlerkurve bezeichnet man die Wahrscheinlichkeitskurve die angibt, nach welcher Lastspielzahl eine Probe bei gegebener Spannungsamplitude voraussichtlichen zu Bruch gehen wird. Wöhlerkurven gelten immer nur für eine bestimmte Mittelspannung!
Anmerkung: Die Wöhlerkurve dient lediglich der Auswertung von Dauerschwingversuchen. Für den Ingenieur ist ein solches Diagramm wenig aufschlussreich, da das Wöhlerdiagramm nur auf eine Mittelspannung beschränkt bleibt. Man erstellt deshalb spezielle Dauerfestigkeitsschaubilder. Von besonderer Bedeutung sind die Dauerfestigkeitsschaubilder nach Haigh und Smith. Im Artikel Dauerfestigkeitsschaubild nach Haigh und Smith finden sich mehr Informationen hierüber.
Festigkeitsbereiche
Prinzipiell können im Wöhlerdiagramm drei Bereiche unterschieden werden. Bei großen Amplituden bricht die Probe bereits nach relativ wenigen Lastspiele. Dies kennzeichnet den Bereich der sogenannten Kurzeitfestigkeit. Dieser Bereich wird oft auch Low-Cycle-Fatigue genannt (kurz: LCF-Bereich). Eine Probe hält in diesem Bereich nur etwa maximal 10.000 bis 100.000 Lastspielen bis zum Bruch stand. Dieser Bereich hat in der Praxis kaum Bedeutung und wird daher auch fast nicht geprüft, da für die meisten Anwendungen deutlich höhere Lastspiele gefordert werden.
Mehr Bruchlastspiele sind nur dann möglich, wenn die Spannungsamplitude entsprechend stärker verringert wird. Im Diagramm zeigt sich dies in der rasch abfallenden Wöhlerkurve. Dieses Abfallen kennzeichnet den Bereich der Langzeitfestigkeit. Der Bereich der Langzeitfestigkeit wird oft auch High-Cycle-Fatigue genannt. Der Übergang vom Kurzzeitfestigkeitsbereich in den Langzeitfestigkeitsbereich ist stets fließend und unterliegt keiner festen Definition.
Höhere Lastspielzahlen können nur noch mit deutlich verringerter Spannungsamplitude erzielt werden. Schließlich tritt unterhalb einer bestimmten Spannungsamplitude dann praktisch kein Bruch mehr ein. Die Wöhlerkurve geht dementsprechend in eine horizontale Linie über. Dies kennzeichnet den Dauerfestigkeitsbereich. Bei ferritischen Stählen zeigt sich der Dauerfestigkeitsbereich ab Lastspielzahlen zwischen 1 Millionen und 10 Millionen. Proben, die bis zu dieser Lastspielzahl den Dauerschwingversuch ohne Bruch durchlaufen, nennt man Durchläufer und gelten als dauerfest.
Beachte: Entspricht die Spannungsamplitude bei einer reinen Zug-Druck-Wechselbeanspruchung gerade der Zugfestigkeit des Probenmaterials, so wird die Probe noch innerhalb des ersten Lastspiels zu Bruch gehen. Deshalb nähert sich in diesem Fall die Wöhlerkurve für kleiner werdende Bruchlastspielzahlen immer mehr dem Wert der Zugfestigkeit an.
Im Bereich der selten geprüften Kurzzeitfestigkeit gehen Proben bereits nach wenigen Lastspielzahlen zu Bruch (<100.000). Im Bereich der Langzeitfestigkeit betragen die Bruchlastspielzahlen bis zu 10.000.000. Über diese Lastspielzahl hinaus gelten die Proben als dauerfest (Dauerfestigkeitsbereich).
Einfluss der Mittelspannung auf die Wöhlerkurve
Besonderen Einfluss auf den Verlauf der Wöhlerkurve hat die Mittelspannung. So werden bei identischer Spannungsamplitude, die Ober- und Unterspannungen durch die höhere Mittelspannung (\(\sigma_m>0\)) entsprechend größer. Folglich wird die Probe stärker beansprucht. Trotz gleicher Spannungsamplitude bricht die Probe dann bereits bei geringeren Lastspielzahlen. Gleiche Bruchlastspielzahlen können bei größerer Mittelspannung folglich nur durch eine entsprechende Verringerung der Spannungsamplitude erzielt werden. Die Wöhlerkurve wird für Mittelspannungen \(\sigma_m>0\) deshalb nach unten verschoben.
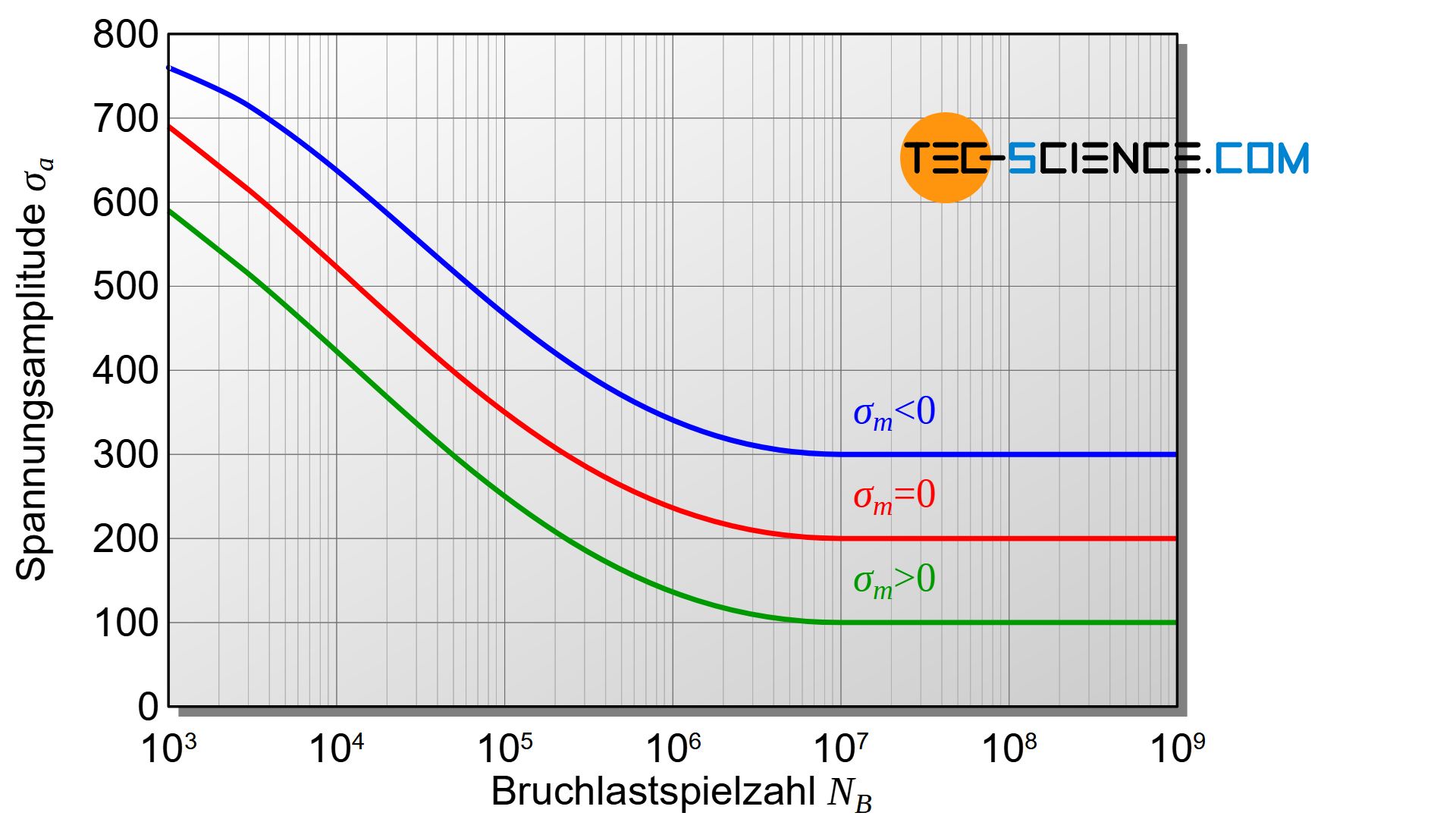
Werden die Mittelspannungen bei dynamischer Zug-Druck-Beanspruchung hingegen nicht in den Zugbereich, sondern in den negativen Druckbereich verschoben (\(\sigma_m<0\)), so zeigt sich innerhalb gewisser Grenzen der gegenteilige Effekt. Die Probe bricht bei unveränderter Spannungsamplitude dann erst bei größeren Lastspielzahlen. Dies bedeutet, dass bei vorgegebener Bruchlastspielzahl die Spannungsamplitude für Mittelspannungen \(\sigma_m<0\) folglich erhöht werden kann. Die Wöhlerkurve ist nach oben hin verschoben.
Ursache der erhöhten Schwingfestigkeit bei Mittelspannung im Druckbereich, liegt im Bruchmechanismus begründet. So erfolgt der Ermüdungsbruch meist ausgehend von Mikrorissen in der Probenoberfläche. Diese Mikrorisse reißen bei Zugbeanspruchung immer mehr auf. Somit breitet sich der Riss mit jedem Lastspiel stärker ins Materialinnere aus. Bei einer Druckbeanspruchung hingegen schließen sich die Risse sozusagen und die Rissbildung bzw. Rissausbreitung wird erschwert (mehr hierzu im Abschnitt Bruchmechanismus).
Bei größeren Mittelspannungen im Zugbereich wird die Wöhlerkurve zu niedrigeren Spannungsamplituden hin verschoben!
Somit wirken sich in vielen Fällen Druckspannungen günstiger auf die Schwingfestigkeit aus als Zugspannungen. Auf diesem Prinzip beruht letztlich auch das Einbringen von Druckeigenspannungen durch Kugelstrahlen (mehr hierzu im Abschnitt Beeinflussung der Schwingfestigkeit).
Dauerfestigkeit und Zeitfestigkeit
Bei kubisch-raumzentrierten Werkstoffen lässt sich häufig eine ausgeprägte Dauerfestigkeit feststellen (horizontale Linie im Wöhlerdiagramm). Hingegen stellt man bei kubisch-flächenzentrierten Werkstoffen meist keine Dauerfestigkeit im eigentlichen Wortsinne fest. Für diese Werkstoffe fällt die Wöhlerkurve über den gesamten Lastspielzahlbereich kontinuierlich ab. Auch korrosive Medien können ein solches Verhalten hervorrufen.
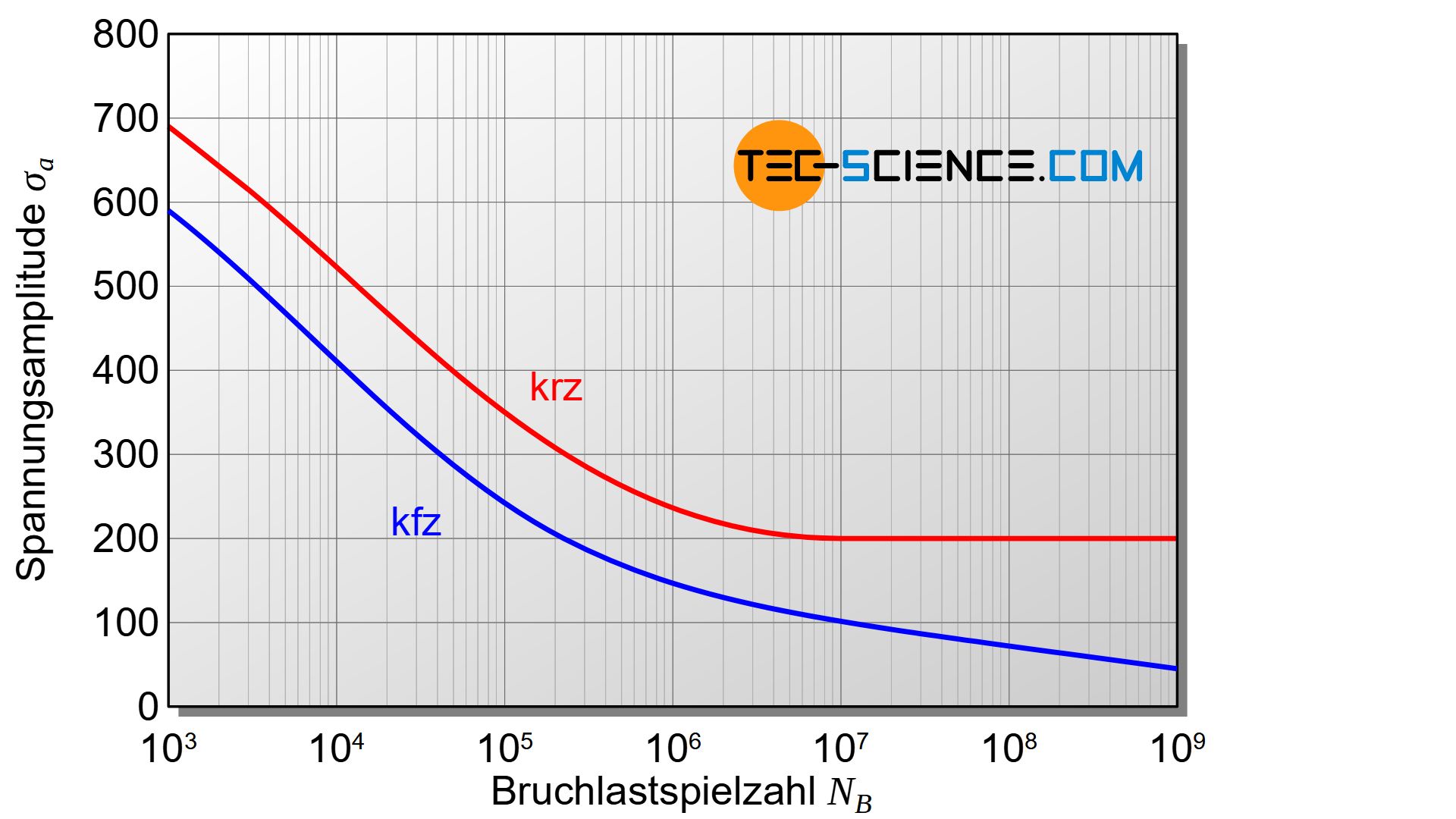
Dies bedeutet, dass selbst bei noch so kleinen Spannungsamplituden die Probe bei hinreichend großer Lastspielzahl irgendwann zu Bruch geht. In der Praxis treten in vielen Fällen jedoch selten mehr als 100 Millionen Lastspiele auf. Aus diesem Grund werden auch solche Proben als „dauerfest“ bezeichnet, die 100 Millionen Lastzyklen durchstehen. Dies entspräche bei einer Frequenz von einem Lastspiel pro Sekunde immerhin einer Beanspruchungsdauer von über 3 Jahren.
Dauerfestigkeit
Die Spannungsamplitude welche eine Probe gerade noch ohne Bruch aushält, wird als Dauerschwingfestigkeit \(\sigma_d\) bezeichnet (kurz: Dauerfestigkeit). Die Angabe der Dauerfestigkeit beinhaltet die Mittelspannung \(\sigma_m\) und die Spannungsamplitude \(\sigma_a\):
\begin{align}
\label{dauerschwingfestigkeit}
&\boxed{\sigma_d = \sigma_m \pm \sigma_a} ~~~~~\text{Angabe der Dauerfestigkeit} \\[5px]
\end{align}
Als Dauerfestigkeit bezeichnet man die Spannungsamplitude, die ein Werkstoff bei gegebener Mittelspannung auf Dauer oder für hinreichend lange Lastspielzahlen ohne Bruch ertragen kann!
Wichtige Spezialfälle ergeben sich für den Fall einer rein wechselnden Beanspruchung (\(R=-1\)) und einer rein schwellenden Beanspruchung (\(R=0\)). Für den Fall der reinen Wechselbeanspruchung mit \(\sigma_m=0\), wird die Dauerfestigkeit dann als Wechselfestigkeit \(\sigma_w\) bezeichnet. Für eine reine Schwellbeanspruchung mit \(\sigma_m=\sigma_a\) nennt man die Dauerfestigkeit auch Schwellfestigkeit \(\sigma_{sch}\).
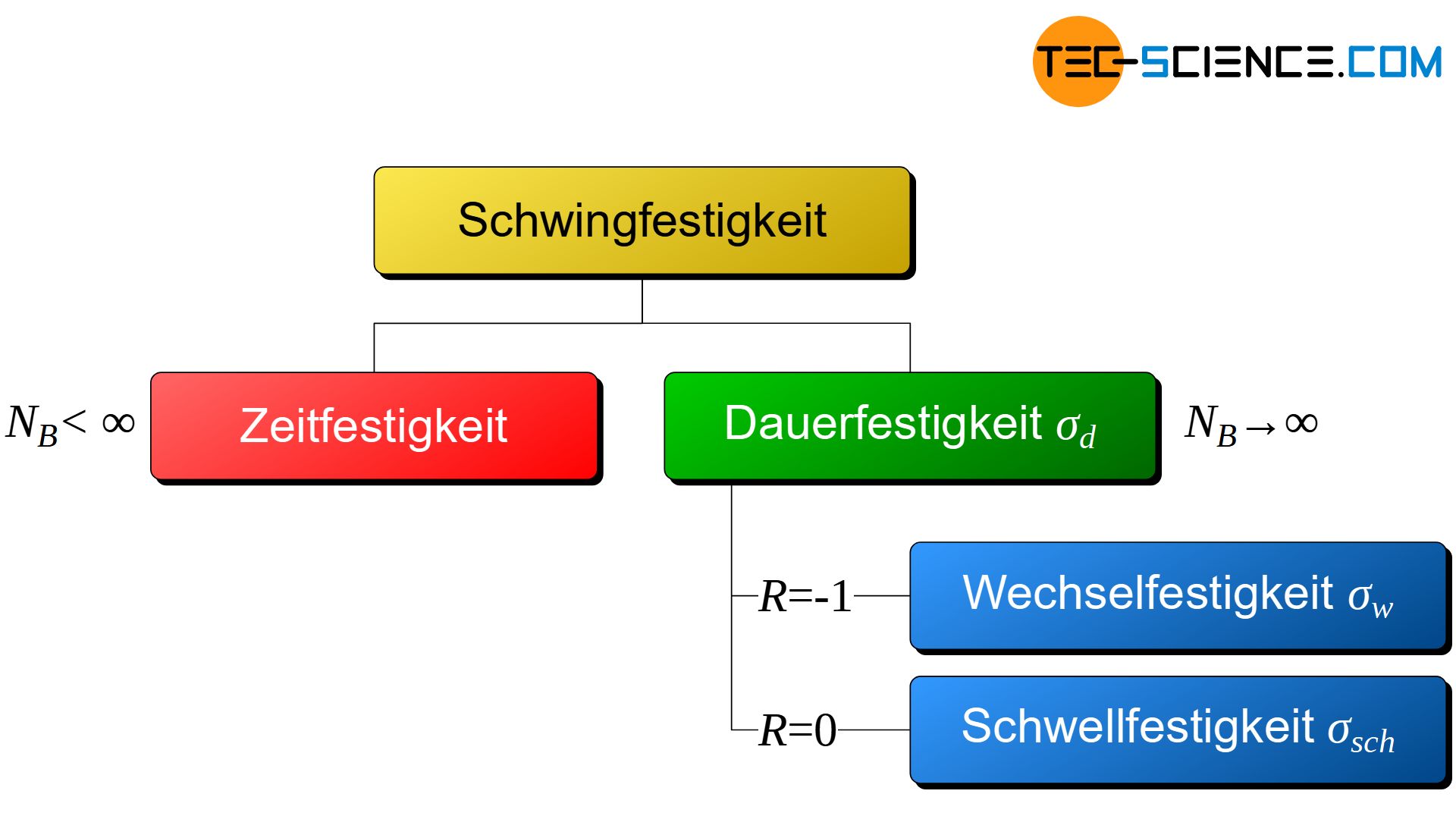
Die Wechselfestigkeit und Schwellfestigkeit sind Spezielfälle für Dauerfestigkeiten für eine rein wechselnde Belastung (Mittelspannung = 0) bzw. eine rein schwellende Belastung (Mittelspannung = Amplitudenspannung)!
Zeitfestigkeit
Auch wirtschaftlichen Gründen sind dynamisch beanspruchte häufig nicht auf Dauerfestigkeit ausgelegt. Denn in der Regel werden Bauteile nicht unendlich oft beansprucht, sondern nur innerhalb ihrer vorgesehenen Einsatzzeit. So sind bspw. Schlagbohrmaschinen nicht darauf ausgelegt unzählige Jahre ohne Schaden zu überdauern. Man schreibt solchen Bauteilen im Allgemeinen lediglich eine bestimmte Lastspielzahl zu, welche sie ohne Schaden überstehen müssen. Diese Betriebsfestigkeit wird dann nicht als Dauerfestigkeit, sondern als Zeitschwingfestigkeit bezeichnet (kurz: Zeitfestigkeit).
Als Zeitfestigkeit bezeichnet man die Spannungsamplitude, die ein Werkstoff bei gegebener Mittelspannung für eine bestimmte Lastspielzahl ohne Bruch ertragen kann!
Bruchmechanismus
Um die Schwingfestigkeit von Bauteilen zu beeinflussen, muss zunächst verstanden werden welche Mechanismen der Entstehung eines Ermüdungsbruchs zugrunde liegen.
Stadien der Rissbildung
Ursache für die einsetzende Ermüdung sind zunächst Risse oder sonstige Oberflächenfehler in der Probenoberfläche. Mikroskopisch betrachtet ist nämlich keine Werkstoffoberfläche perfekt glatt und eben. Vielmehr weist sie Rauigkeiten und feinste Risse auf oder sonstige Einschlüsse auf. Solche Rauigkeiten wirken wie kleine Kerben an denen erhöhte Spannungen mit dreiachsigem Spannungszustand entstehen. Diese Spannungen können dann weit über den einachsigen Nennspannungen liegen.
An diesen Fehlstellen wird die Fließgrenze dann lokal überschritten und es kommt zu mikroplastischen Verformungen. Es bilden sich Materialverschiebungen durch auslaufende Gleitebenen. Solche Verschiebungen lassen entweder Ausbuchtungen (Extrusionen) oder Einbuchtungen (Intrusionen) an der Oberfläche zurück. Diese mikroskopischen Verwerfungen dienen wiederum als Kerben und verstärken somit die Rissbildung (Stufe I).
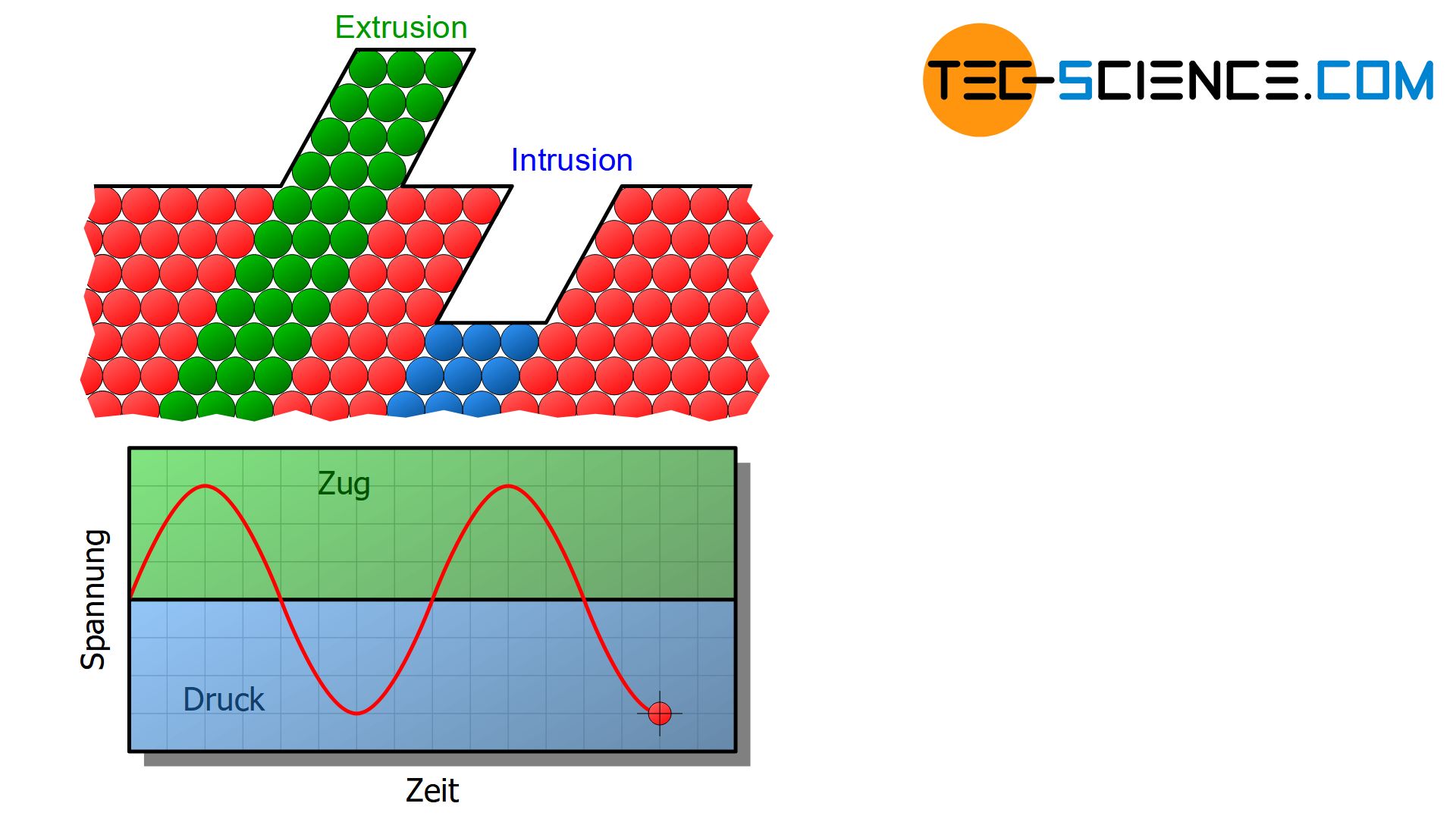
Infolge der plastischen Mikroverformung kann es zu Verfestigungen und damit zu einem Versetzungsaufstau kommen. In der Folge wird der Werkstoff an diesen Stellen lokal verspröden. Das Material bricht bei einem Lastwechsel mehr und mehr auf und der Anriss schreitet tiefer ins Innere fort. Diese Rissausbreitung kennzeichnet das Einsetzen des Ermüdungsbruchs (Stufe II). Bis es jedoch zum endgültigen Bruch kommt, werden in der Regel noch unzählige Lastwechsel vergehen.
Mit fortschreitender Rissausbreitung nimmt der tragende Restquerschnitt immer mehr ab. Auf diese Weise verteilt sich die Last auf eine immer kleinere Fläche. Früher oder später kann der abnehmende Querschnitt der Beanspruchung nicht mehr standhalten. Die Zugfestigkeit wird im Restquerschnitt überschritten und das Bauteil bricht (Stufe III). Die Bruchfläche zeigt in diesem Bereich je nach Werkstoff das typische Merkmal eines spröden oder duktilen Gewaltbruchs wie man es vom Zugversuch her kennt.
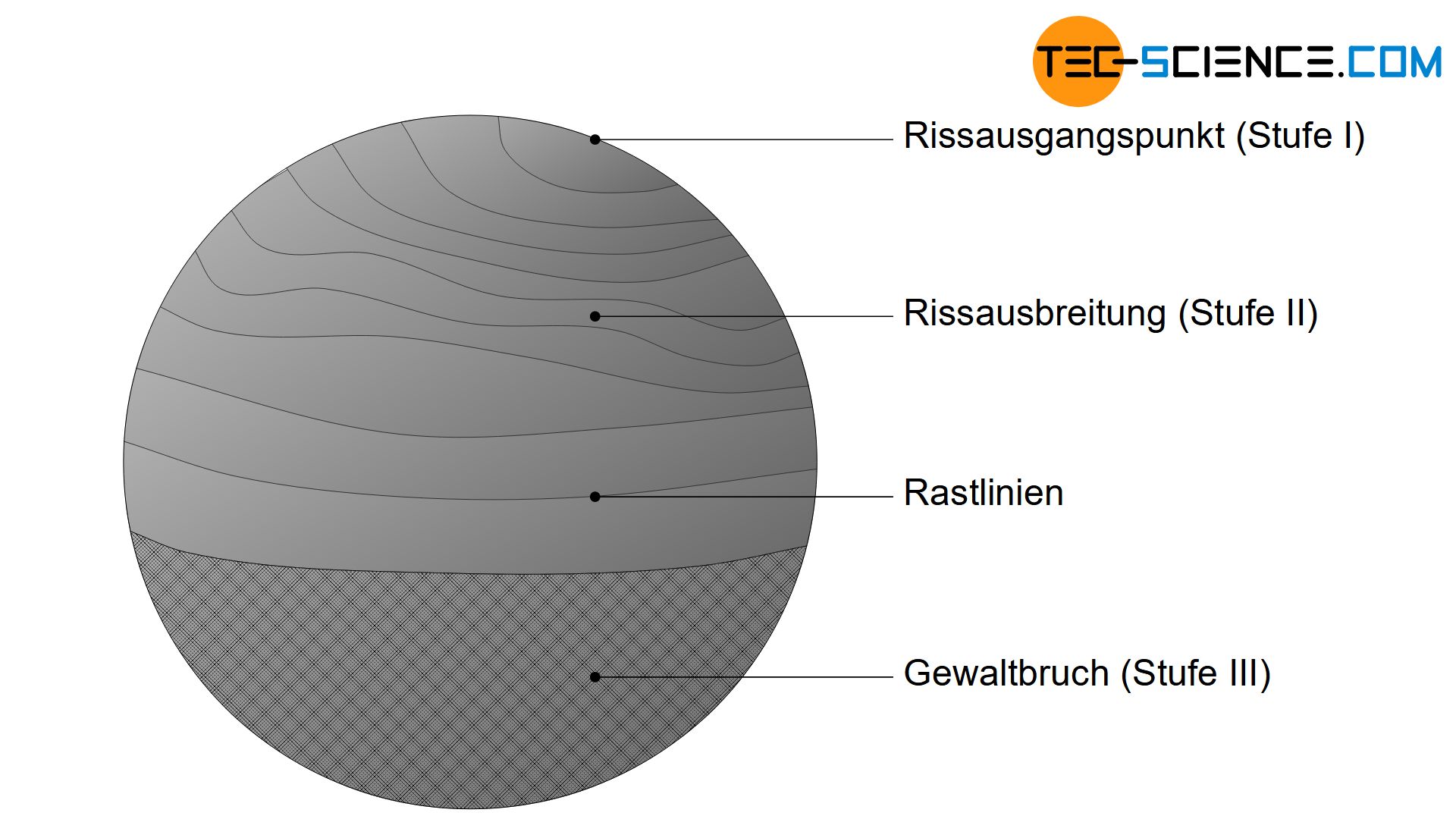
Spannungserhöhungen an Fehlstellen führen zur lokalen Überschreitung der Fließgrenze und damit zur Bildung eines ersten Anrisses (Stufe I). Der Riss breitet sich mehr und mehr aus (Stufe II), bis es durch die Abnahme des tragenden Querschnitts schließlich zum Gewaltbruch kommt (Stufe III)!
Schwingungsstreifen und Rastlinien
Aufgrund des zyklischen Voranschreitens des Risses bei jedem Lastwechsel, ergeben sich während der Rissausbreitungsphase (Stufe II) typische Schwingungsstreifen im Material. Die Schwingungsstreifen werden auch kurz als Schwingstreifen bezeichnet. Diese feinen Strukturen sind zunächst nur mit Hilfe von Rasterelektronenmikroskopen oder Rastertunnelmikroskopen auflösbar.
Immer wenn sich im Beanspruchungsverlauf jedoch eine starke Änderung ergibt, können die Schwingungsstreifen als sogenannte Rastlinien zum Vorschein. Diese Linien sind dann mit bloßem Auge sichtbar (siehe Abbildung oben). Zu den besagten Beanspruchungsänderungen gehören nicht nur die namensgebenden Rastphasen (Ruhephasen) sondern auch starke Lastwechsel, die sowohl richtungsbedingt als auch intensitätsbedingt sein können. Eine solche mehrstufige Belastung liegt in der Realität meist vor, da viele Bauteile wie bspw. Antriebswellen von Automobilen in der Regel nie gleichmäßig dynamisch beansprucht sind.
Rastlinien werden deshalb sichtbar, weil mit den Beanspruchungsänderungen auch immer eine Änderung in der Rissausbreitungsgeschwindigkeit verbunden ist. Dies wiederum hat Auswirkungen auf die Oxidation der Rissfront. Solch unterschiedlich stark oxidierten Rissfronten sind dann mit bloßem Auge erkennbar.
Rastlinien sind sichtbare Linien auf der Bruchfläche, die während der Phase der Rissausbreitung aufgrund von unterschiedlich starken Oxidationsvorgängen bei Laständerungen entstehen!
Da die Rastlinien stets senkrecht zur Rissausbreitungsrichtung liegen, kann anhand deren Anordnung auch relativ einfach der Rissausgangspunkt ermittelt werden. Sind darüber hinaus die zeitlichen Abstände der Belastungsänderungen bekannt, welche jeweils eine Rastlinie hinterlassen, so kann anhand der Rastlinienanzahl auch auf den Zeitpunkt des Rissausbreitungsbeginns geschlossen werden (ähnlich den Jahresringen eines Baumes).
Bruchfläche
Äußerlich kann der Ermüdungsbruch also an seinen zwei typischen Bruchbereichen erkannt werden. Im Bereich der Rissausbreitung zeigen sich die charakteristischen Rastlinien oder zumindest Schwingungsstreifen. Diese Schwingbruchfläche ist aufgrund der permanenten mikroskopischen Reibung der beiden Bruchhälften meist relativ glatt. Im Gegensatz hierzu weist die Gewaltbruchfläche (Restbruchfläche) eine eher zerklüftete Oberflächenstruktur auf.
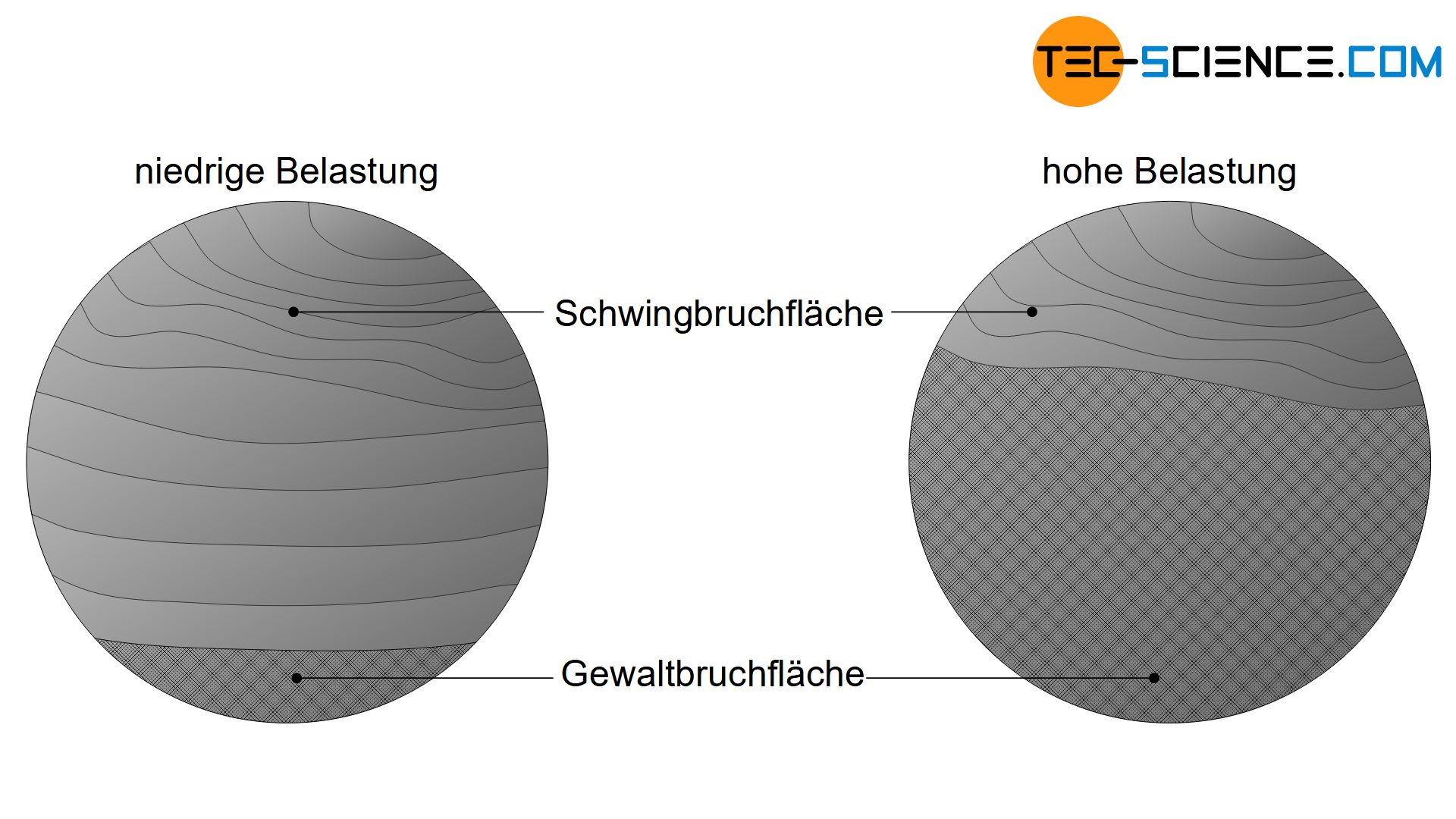
Ein Ermüdungsbruch ist meist anhand der Bruchfläche durch zwei abgrenzbare Bereiche gekennzeichnet: Bereich der Rissausbreitung mit sichtbaren Rastlinien und den Bereich des Gewaltbruchs!
Anhand des Verhältnisses von Schwingbruchfläche und Gewaltbruchfläche lässt sich auch auf die Höhe der dynamischen Belastung schließen. Relativ große Gewaltbruchflächen deuten auf eine hohe Belastung hin, verhältnismäßig geringe Gewaltbruchflächen hingegen auf eine eher niedrige Belastung.
Anmerkung: An den gebrochenen Proben im Dauerschwingversuch sind in der Regel keine Rastlinien wiederzufinden, da es sich dabei nicht um eine mehrstufige, sondern um eine einstufige Belastung mit konstanter Spannungsamplitude handelt (gleichmäßige dynamische Beanspruchung).
Beeinflussung der Schwingfestigkeit
Wie im Abschnitt Bruchmechanismus erläutert, bilden meist Fehlstellen an der Oberfläche von Bauteilen den Ausgangspunkt einer Rissbildung. Mikrorisse an der Oberfläche von rauen Proben oder scharfe Kanten (z.B. bei Bohrungen) wirken wie Kerben an denen sehr hohe Spannungsspitzen entstehen. Dies gilt auch für korrodierte Stellen. All diese Oberflächenstellen begünstigen die Rissbildung und das vorzeitige Brechen der Probe.
Einfluss der Bauteiloberfläche und Bauteilgeometrie
Offensichtlich hat die Qualität der Probenoberfläche besonderen Einfluss auf die Bruchlastspielzahl. Polierte Proben mit weichen Geometrieübergängen weisen deshalb in der Regel höhere Schwingfestigkeitswerte auf. Aus diesem Grund sollten bei dynamisch beanspruchten Bauteilen Kerben, Kanten und scharfe Übergänge vermieden werden.
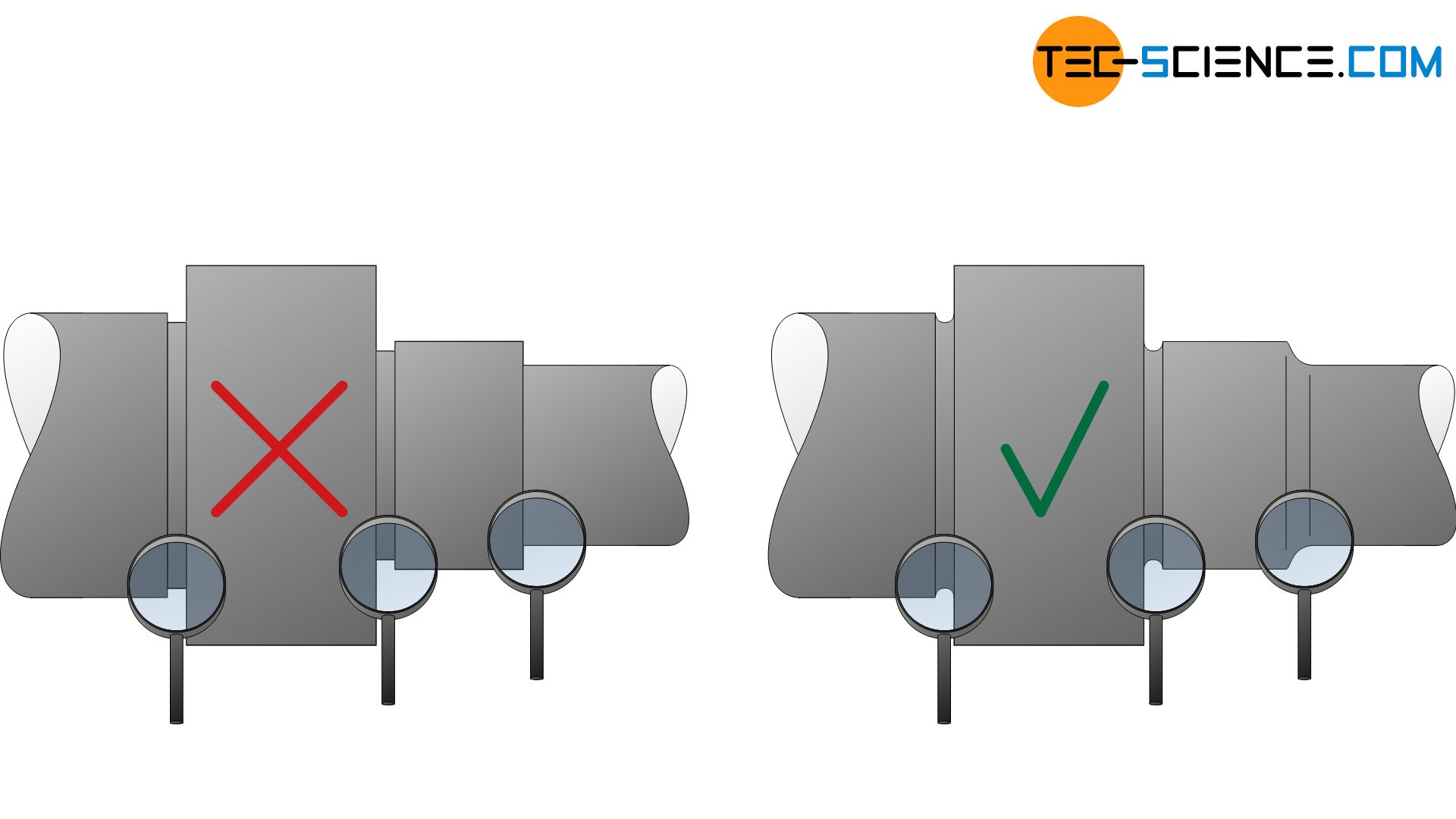
Scharfe Geometrieübergänge an Bauteilen sollten zur Vermeidung von Spannungsspitzen vermieden werden, um die Schwingfestigkeit zu erhöhen!
Einfluss von Druckeigenspannungen
Auch die dynamische Vorbeanspruchung der Probe hat Einfluss auf die Schwingfestigkeit. Wird eine Probe bereits im Vorfeld mit relativ geringer Spannungsamplitude dynamisch vorbeansprucht, so kann sich dies durchaus positiv auf die Schwingfestigkeit auswirken. Eine solche vorbeanspruchte Probe kann bei einer anschließenden Dauerschwingprüfung höheren Lastspielzahlen standhalten als eine neuartige Probe.
Diese mag zunächst paradox erscheinen, liegt jedoch in der Verfestigung der Oberfläche und den hierdurch entstehenden Druckeigenspannungen begründet. Unter Druckspannungen wird die Rissbildung bzw. Rissausbreitung nämlich gehemmt, da die Druckkräfte praktisch versuchen einen möglichen Riss zu schließen und nicht weiter aufzureißen.
Vorbeanspruchungen von Bauteilen können sich durch Verfestigungseffekte positiv auf die Schwingfestigkeit auswirken!
Das Einbringen von Druckeigenspannungen kann bspw. durch Kaltverfestigung, Randschichthärten oder Kugelstrahlen erfolgen. Beim Kugelstrahlen werden feine Partikel mit hoher Geschwindigkeit auf die Bauteiloberfläche geschossen. Auf diese Weise entstehen an der Oberfläche plastische Verformungen, die in den umliegenden elastischen Bereichen dann zu Druckeigenspannungen führen. Sehr häufig wird das Kugelstrahlen bspw. bei Federn angewendet.
Besondere Bedeutung zur Steigerung der Schwingfestigkeit durch Einbringen von Druckeigenspannungen hat auch das Randschichthärten in Form von Nitrierhärten. Die sich an der Bauteiloberfläche zu Nitriden verbindenden Legierungselemente erzeugen durch ihre Volumenvergrößerung hohe Druckeigenspannungen.
Das Einbringen von Druckeigenspannungen (bspw. durch Kugelstrahlen oder Nitrieren) kann die Schwingfestigkeit von Bauteilen erhöhen!
Einfluss der Probengröße
Nicht nur die Oberfläche der Probe, sondern auch die Probengröße bzw. Bauteilgröße selbst beeinflusst die Schwingfestigkeit. So weisen größere Proben statistisch bedingt mehr „Störstellen“ auf als kleinere Proben. Bei identischem Werkstoff zeigen deshalb größere Proben in der Regel auch geringere Dauerfestigkeitswerte als kleinere Proben mit geometrisch ähnlichen Abmessungen. Dieses Phänomen zeigt sich vor allem bei Biege- und Torsionsbeanspruchungen, welche einen linearen Spannungsverlauf im Bauteil verursachen und so die größten Spannungswerte im Bereich der Oberfläche entstehen lassen.
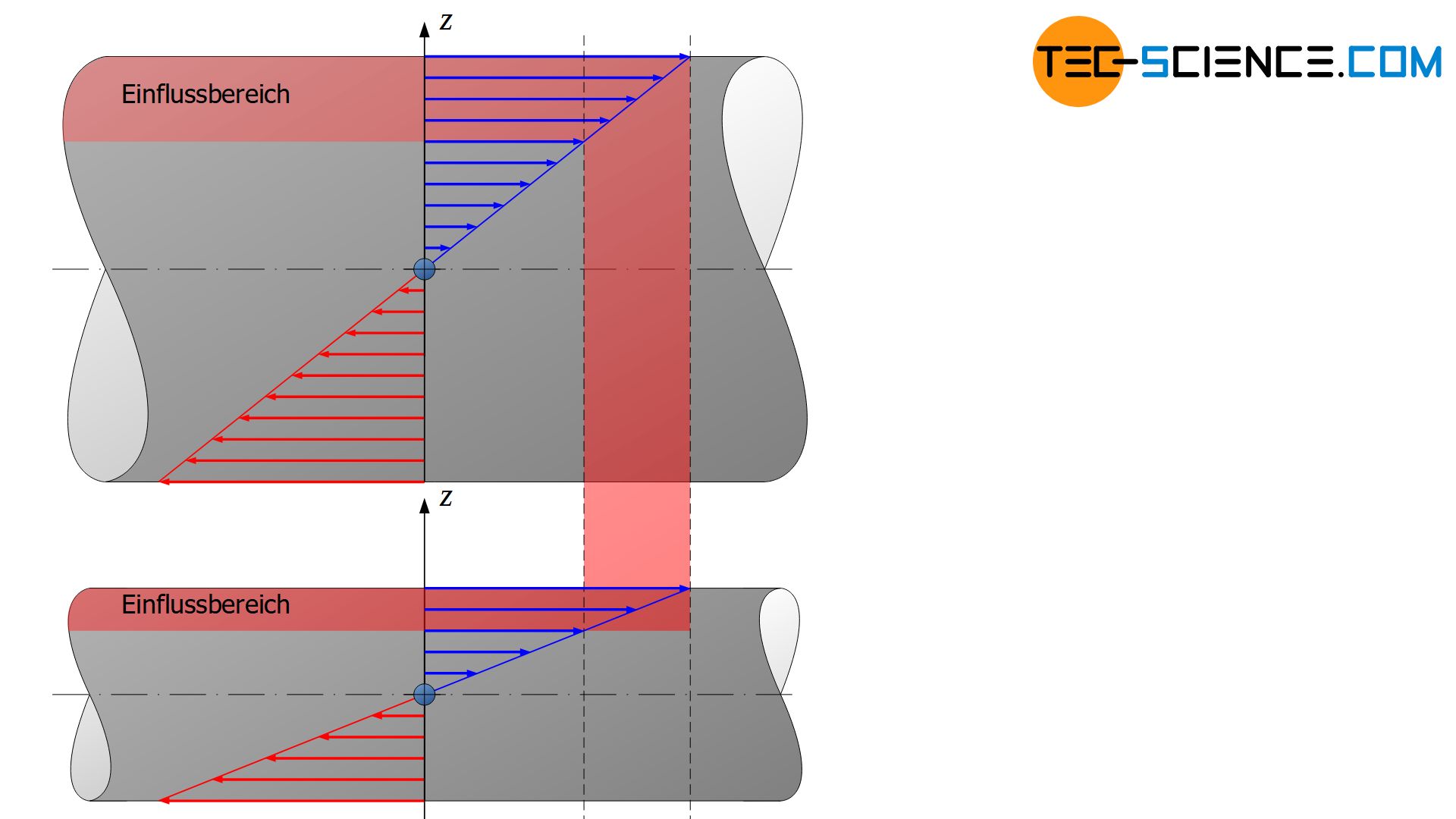
Die obere Abbildung zeigt den Spannungsverlauf zweier auf Biegung beanspruchter Proben. Bei identischen Biegespannungen umfasst derselbe Spannungsbereich bei der größeren Probe auch einen größeren Oberflächenbereich. Gerade bei diesen Beanspruchungsfällen kommt deshalb dem (vergrößerten oder verkleinerten) Randbereich eine besondere Bedeutung zu und der Einfluss der Bauteilgröße ist entsprechend groß. Bei dynamischen Zug- und Druckbeanspruchungen ist der Größeneinfluss hingegen eher weniger stark ausgeprägt.
Große Bauteile weisen meist geringere Schwingfestigkeiten auf als kleinere Bauteile!
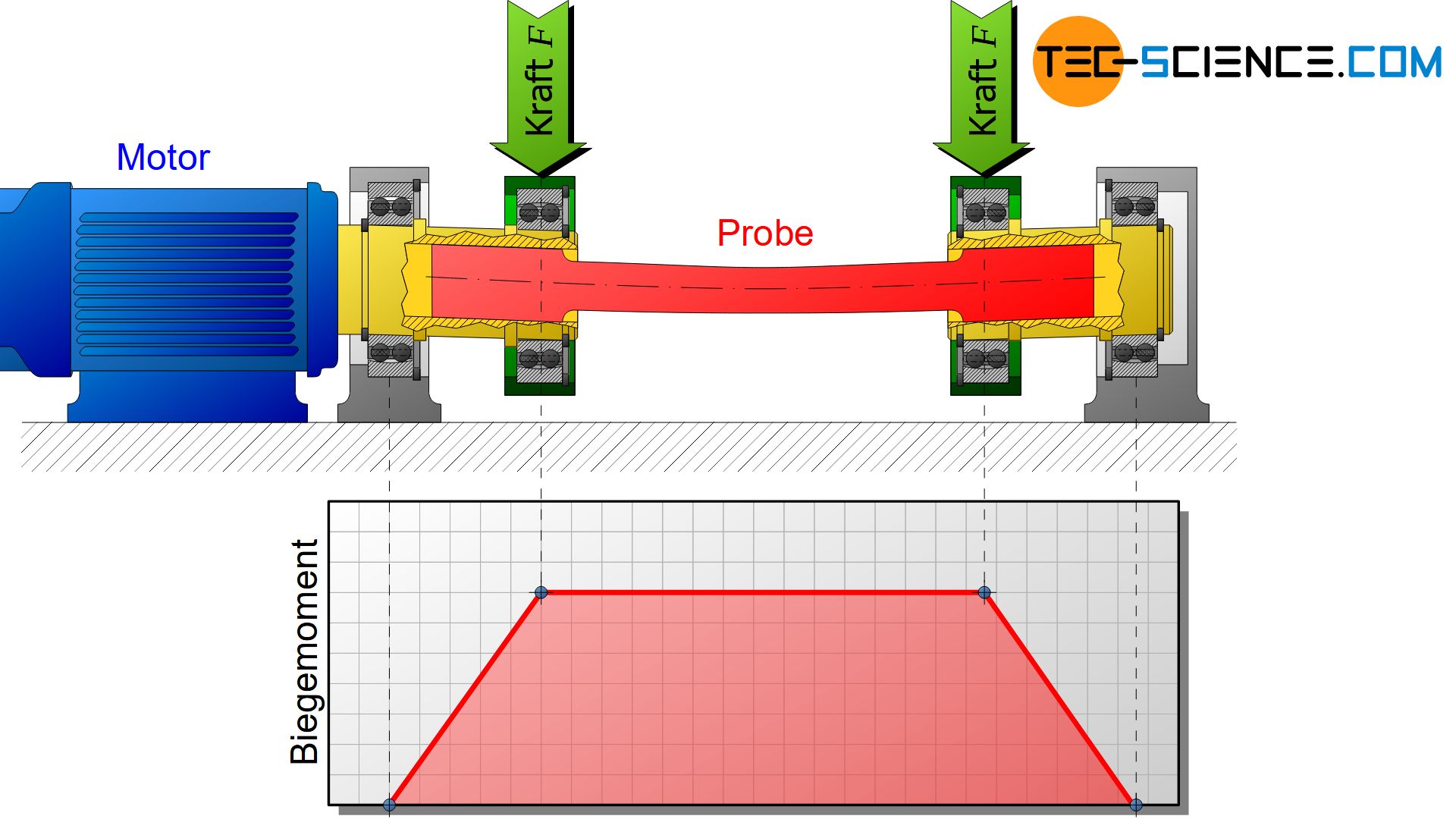
Umlaufbiegeversuch und Flachbiegeversuch
Eine besondere Art des Dauerschwingversuchs ist der Umlaufbiegeversuch nach DIN 50113. Dort rotiert eine auf Biegung beanspruchte Rundprobe, welche auf Biegewechselfestigkeit geprüft werden soll. Durch das konstante Biegemoment und die Rotation ändern sich im Werkstoff permanent die hervorgerufenen Zug- und Druckspannungen. Während eines Umlaufs wird jeder Bereich der Welle einmal auf Zug und eine halbe Umdrehung später auf Druck beansprucht. Auf ähnliche Weise wurde der Flachbiegeschwingversuch nach DIN 50142 für Flachproben entwickelt („Hin- und Herbiegeversuch“).