Herleitung der Formeln für Arbeit und Wärme eines polytropen Prozesses

Erfahre in diesem Artikel mehr über die Herleitung der Formeln für die Berechnung der Arbeit, Wärme und Änderung der inneren Energie bei polytropen Prozessen.

Polytrope Zustandsgleichungen

Im Artikel Polytroper Prozess in einem geschlossenen System wurden die folgenden Zustandsgleichungen zur Beschreibung von polytropen Prozessen hergeleitet und näher diskutiert:

\begin{align}
\label{2716}
\boxed{p \cdot V^n=\text{konstant}} &~~\Rightarrow~~ \boxed{p_1 \cdot V_1^n=p_2 \cdot V_2^n} \\[5px]
\label{4375}
\boxed{T \cdot V^{n-1}=\text{konstant}} &~~\Rightarrow~~ \boxed{T_1 \cdot V_1^{n-1}=T_2 \cdot V_2^{n-1}} \\[5px]
\label{7991}
\boxed{T^n \cdot p^{1-n}=\text{konstant}} &~~\Rightarrow~~ \boxed{T_1^n \cdot p_1^{1-n}=T_2^n \cdot p_2^{1-n}} \\[5px]
\end{align}

In diesem Artikel sollen die Formeln zur Berechnung der Volumenänderungsarbeit und der übertragenen Wärme bei polytropen Prozessen hergeleitet werden.

Herleitung der Formel für die Volumenänderungsarbeit

Die Volumenänderungsarbeit W_V erhält man ganz allgemein durch Integration der p(V)-Funktion des polytropen Prozesses:

\begin{align}
\label{www}
&\boxed{W_\text{V} = – \int\limits_{V_1}^{V_2} p(V) ~ \text{d}V}\\[5px]
\end{align}

Für die Ermittlung der Volumenänderungsarbeit muss also die Funktion p(V) bekannt sein. Wird eine polytrope Zustandsänderung ausgehend eines Anfangszustandes 1 mit den Größen (p₁ und V₁) beschrieben, so kann dann durch Gleichung (\ref{2716}) eine allgemeine Beziehung zu einem beliebig weiteren Zustand 2 (p, V) hergestellt werden. Somit ergibt sich der Druckverlauf p(V) wie folgt:

\begin{align}
\label{9891}
&p_1~V_1^n=p~V^n \\[5px]
\label{1227}
&p = \underbrace{p_1~V_1^n}_{=\text{konstant}} \cdot {1 \over V^n} \\[5px]
\label{9377}
&\boxed{p(V)=p_1~V_1^n \cdot {1 \over V^n}} \\[5px]
\end{align}

Um die Volumenänderungsarbeit W_V zu berechnen kann nun die Druckfunktion (\ref{9377}) innerhalb der Grenzen V₁ bis V₂ integriert werden:

\begin{align}
\label{9445}
W_\text{V} &= – \int\limits_{V_1}^{V_2} p(V) ~ \text{d}V \\[5px]
&= – \int\limits_{V_1}^{V_2} \underbrace{p_1~V_1^n}_{=\text{konstant}} \cdot {1 \over V^n} ~ \text{d}V \\[5px]
&= – p_1~V_1^n~\int\limits_{V_1}^{V_2} {V^{-n}} ~ \text{d}V \\[5px]
&= – p_1~V_1^n~ \left[{1 \over {1-n}}~V^{1-n} \right]_{V_1}^{V_2} \\[5px]
&= – {{p_1~V_1^n} \over {1-n}} ~ \left[V_2^{1-n}-V_1^{1-n} \right] \\[5px]
&= {{p_1~V_1^n} \over {n-1}} ~ \left[V_2^{1-n}-V_1^{1-n} \right] ~~~ \text{nach ausklammern von } V_1^{1-n} \text{ folgt:} \\[5px]
&= {{p_1~V_1^n~V_1^{1-n}} \over {n-1}} ~ \left[{V_2^{1-n} \over V_1^{1-n}} -1 \right] \\[5px]
\end{align}

\begin{align}
\label{8254}
\boxed{W_\text{V}= {{p_1~V_1} \over {n-1}} ~ \left[\left(V_2 \over V_1 \right)^{1-n} -1 \right]}
\end{align}

Die Volumenänderungsarbeit kann vor allem anhand der Temperaturen relativ einfach ermittelt werden. Hierzu wird Gleichung (\ref{4375}) mit Gleichung (\ref{8254}) kombiniert und zusätzlich der Zusammenhang aus der idealen Gasgleichung mit p⋅V=m⋅R_S⋅T genutzt:

\begin{align}
W_\text{V} &= {\overbrace{p_1~V_1}^{=m~R_\text{S}~T_1}\over {n-1}} ~ \left[\left(V_2 \over V_1 \right)^{1-n} -1 \right] \text{mit: } ~{V_2 \over V_1} = \left(T_1 \over T_2 \right)^{1 \over {n-1}}=\left(T_2 \over T_1 \right)^{1 \over {1-n}}~ \text{ folgt : } \\[5px]
&= {{m~R_\text{S}~T_1} \over {n-1}} ~ \left[{T_2 \over T_1} -1 \right] \\[5px]
\label{m}
&= {{R_\text{S} \over {n-1}}} ~m~ \left(T_2 – T_1 \right) ~~~\text{mit } \underline{R_\text{S}=c_\text{p}-c_\text{v}} ~~~\text{folgt:} \\[5px]
&= {{{c_\text{p}-c_\text{v}} \over {n-1}}} ~m~ \left(T_2 – T_1 \right) \\[5px]
&= {{{{c_\text{p}\over c_\text{v}}-1} \over {n-1}}} ~c_\text{v}~m~ \left(T_2 – T_1 \right) ~~~\text{mit } \underline{\kappa={c_\text{p} \over c_\text{v}}} ~~~\text{folgt:} \\[5px]
\label{eq:9418}
\end{align}

\begin{align}
\boxed{W_\text{V}=\left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~ \left(T_2 – T_1 \right)}
\label{2604}
\end{align}

Herleitung der Formel für die übertragene Wärme

Zuletzt bleibt noch die Ermittlung der übertragenen Q während eines polytropen Prozesses. Diese ergibt sich gemäß des ersten Hauptsatzes über die Differenz von innerer Energieänderung ΔU und Volumenänderungsarbeit W_V:

\begin{align}\
&\boxed{ Q + W_\text{V} = \Delta U} ~~~~\text{erster Hauptsatz}\\[5px]
\label{put}
&Q = \Delta U – W_\text{V}\\[5px]
\end{align}

Für ideale Gase ergibt sich die Änderung der inneren Energie ΔU unabhängig des thermodynamischen Prozesses lediglich anhand der Temperaturänderung ΔT=T₂-T₁:

\begin{align}\
\label{9719}
&\boxed{ \Delta U = c_\text{v}~m~\left(T_2-T_1 \right)} \\[5px]
\end{align}

Wird die Änderung der inneren Energie nach Gleichung (\ref{9719}) und die Volumenänderungsarbeit nach Gleichung (\ref{m}) in die Gleichung (\ref{put}) eingesetzt, so ergibt sich für die übertragene Wärme Q eines polytropen Prozesses folgende Formel:

\begin{align}
Q &= \Delta U – W_\text{V} \\[5px]
&= c_\text{v}~m~\left(T_2-T_1 \right) – {R_\text{S} \over {n-1}} ~m~ \left(T_2 – T_1 \right) \\[5px]
&= \left[c_\text{v}-{R_\text{S} \over {n-1}}\right]~m~\left(T_2-T_1 \right) ~~~\text{mit } \underline{R_\text{S}=c_\text{p}-c_\text{v}} ~~~\text{folgt:} \\[5px]
&= \left[c_\text{v}-{{c_\text{p}-c_\text{v}} \over {n-1}}\right]~m~\left(T_2-T_1 \right) \\[5px]
&= \left[{{c_\text{v}~(n-1)}\over {n-1}}-{{c_\text{p}-c_\text{v}} \over {n-1}}\right]~m~\left(T_2-T_1 \right) \\[5px]
&= \left[{{c_\text{v}~n-c_\text{v}-c_\text{p}+c_\text{v}} \over {n-1}}\right]~m~\left(T_2-T_1 \right) \\[5px]
&= \left[{{c_\text{v}~n-c_\text{p}} \over {n-1}}\right]~m~\left(T_2-T_1 \right) \\[5px]
&= \left[{{n-{c_\text{p} \over c_\text{v}}} \over {n-1}}\right]~c_\text{v}~m~\left(T_2-T_1 \right) ~~~\text{mit } \underline{\kappa={c_\text{p} \over c_\text{v}}} ~~~\text{folgt:} \\[5px]
\label{eq:7090}
\end{align}

\begin{align}
\boxed{Q= \left[{{n-\kappa} \over {n-1}}\right]~c_\text{v}~m~\left(T_2-T_1 \right)}
\label{eq:8691}
\end{align}

Zusammenfassung

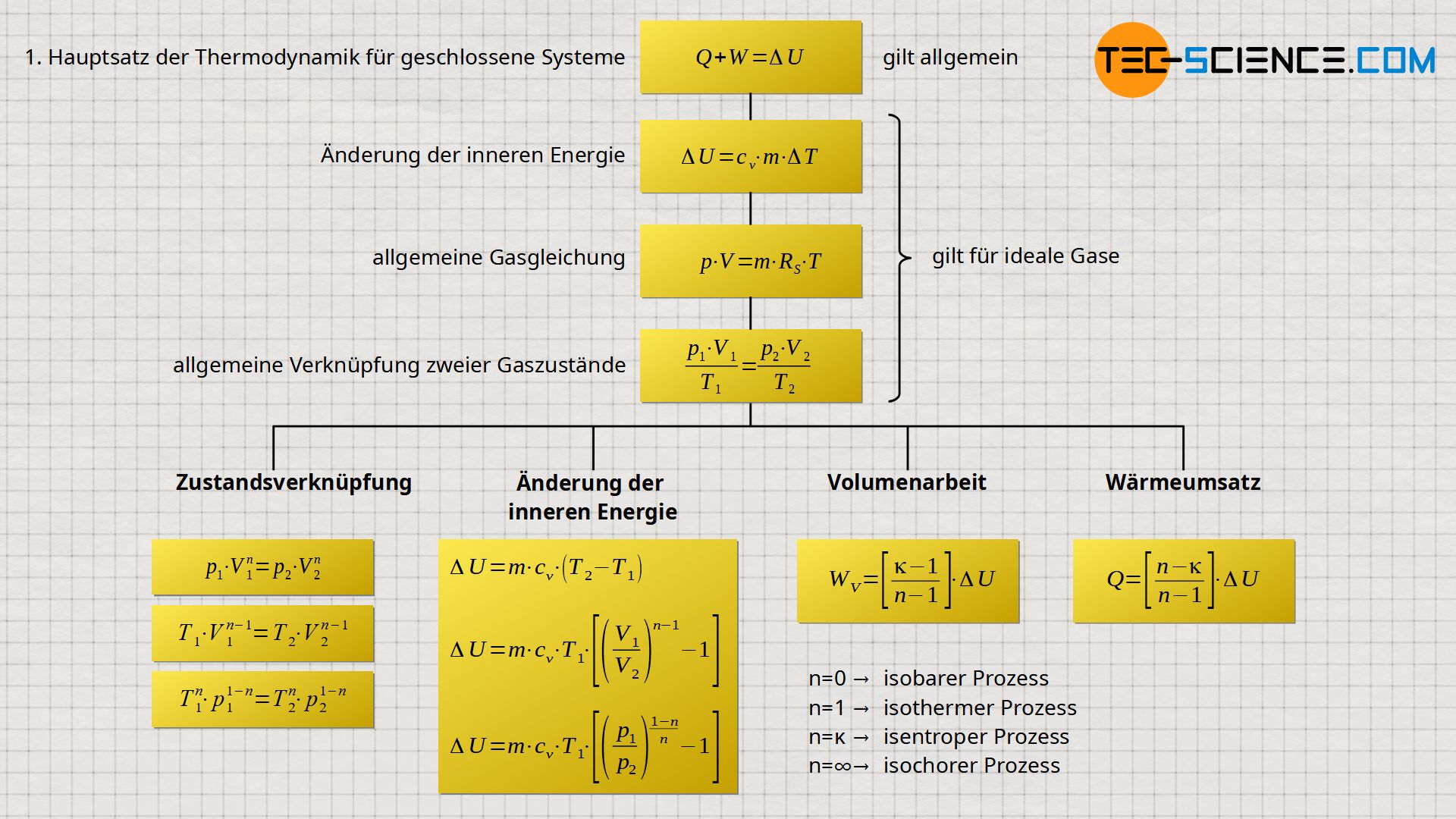
Die gesamten hergeleiteten Formeln zur Berechnung von Wärme, Arbeit und Änderung der inneren Energie, können in Kombination mit Gleichung (\ref{4375}) bzw. Gleichung (\ref{7991}) auch über das Volumen- bzw. Druckverhältnis ausgedrückt werden. Somit ergeben sich für die Berechnung der Arbeit, der Wärme und der Änderung der inneren Energie folgende Formeln für einen polytropen Prozess:

\begin{alignat}{2}
\label{6005}
&{W_\text{V} = \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~\left(T_2-T_1 \right)}& &= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[\left(T_2\over T_1\right)-1 \right] \\[5px]
&&&= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[20px]
\label{1733}
&{Q = \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~\left(T_2-T_1 \right)}& &= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[\left(T_2\over T_1\right)-1 \right] \\[5px]
&&&= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[20px]
&{\Delta U = c_\text{v}~m~\left(T_2-T_1 \right)}& &= c_\text{v}~m~T_1~\left[{T_2 \over T_1}-1 \right] \\[5px]
&&&= c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&=c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[5px]
\end{alignat}

Betrachtet man die Gleichungen (\ref{6005}) und (\ref{1733}) genauer, so fällt auf, dass der darin enthaltene Term c_v⋅m⋅(T₂-T₁) letztlich der Änderung der inneren Energie ΔU entspricht. Somit kann die Volumenänderungsarbeit W_V und der Wärmeumsatz Q auch in Abhängigkeit der Änderung der inneren Energie ΔU berechnet werden:

\begin{align}
\label{6763}
&\boxed{W_\text{V}= \left[{{\kappa-1} \over {n-1}}\right] ~\Delta U} \\[5px]
&\boxed{Q= \left[{{n-\kappa} \over {n-1}}\right] ~\Delta U} \\[5px]
\end{align}