Gesetz von Gay-Lussac für ideale Gase

Das Gesetz von Gay-Lussac beschreibt die Zunahme des Volumens bei zunehmender Temperatur für eine Zustandsänderung bei konstantem Druck (isobarer Prozess).

Isobare Zustandsänderung

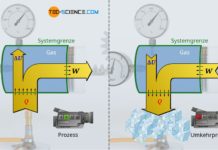
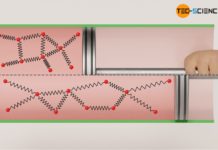
Erfolgen thermodynamische Prozesse bei konstantem Druck, so werden diese auch als isobare Zustandsänderungen bezeichnet. Eine solche isobare Zustandsänderung zeigt sich zum Beispiel, wenn ein Gas in einem Zylinder mit beweglichem Kolben eingeschlossen ist. Wird das Gas nun erwärmt, dann dehnt es sich isobar aus und das Volumen vergrößert sich dementsprechend. Die genauere Abhängigkeit des Gasvolumens von der Temperatur während einer solchen isobaren Zustandsänderung eines geschlossenen Systems soll im Folgenden näher untersucht werden.

Experimentelle Untersuchung

Versuchsaufbau

Zur Untersuchung der Zusammenhänge wird im Prinzip der oben beschriebene Aufbau von Zylinder und Kolben verwendet. Der Zylinder ist über einen Schlauch mit einem größeren Gefäß verbunden, um das Gasvolumen zu erhöhen. Hierdurch wird die Messgenauigkeit gesteigert, da sich insgesamt mehr Gas ausdehnen kann und somit eine größere Volumenänderung resultiert. Im einfachsten Fall wird Luft als Gas verwendet, das näherungsweise als ideales Gas betrachtet werden kann. Am Zylinder ist eine Skala angebracht, an der die Volumenänderung abgelesen werden kann. Das Gesamtvolumen ergibt sich aus der Summe von Gefäßvolumen, Zylindervolumen und Volumen des Schlauchs.

Wird die Luft nun erwärmt, dehnt sie sich entgegen des herrschenden Umgebungsdrucks aus und drückt den Kolben nach oben. Einerseits würde bei konstantem Volumen der Druck aufgrund des Temperaturanstiegs ansteigen (Gesetz von Amontons). Andererseits würde bei konstanter Temperatur der Druck aufgrund der Volumenzunahme abnehmen (Gesetz von Boyle-Mariotte). Beide Effekte heben sich letztlich gegenseitig auf, wenn sich das Volumen des Gases frei ausdehnen kann. Insgesamt ergibt sich im vorliegenden Fall somit keine Druckänderung. Das sich ausdehnende Gas gibt dem Druckanstieg sozusagen permanent nach. Hierbei ist es der umgebende Luftdruck und die Gewichtskraft des Kolbens, die dem Gas seinen konstanten Druck aufzwingen. Der thermodynamische Prozess läuft also isobar ab.

Die Luft im Gefäß wird mit Hilfe eines Wasserbades erwärmt. Messunsicherheiten kommen an dieser Stelle durch die ungleichmäßige Erwärmung zustande, da nur die Luft im Gefäß nicht aber im Schlauch und im Zylinder erwärmt wird. Um den Messunsicherheit so gering wie möglich zu halten, sollte das Volumen im Schlauch und im Kolben so klein wie möglich gehalten werden. Alternativ kann die gesamte Messapparatur in ein Wasserbad gestellt werden. Auf diese Weise kann schließlich die Abhängigkeit des Gasvolumens von der Temperatur bei konstantem Druck untersucht werden.

Linearität zwischen Volumen und Temperatur (Einheit: Grad Celsius)

Wie bereits angedeutet, stellt man während der Durchführung des Versuchs bereits fest, dass sich das Volumen vergrößert, wenn sich die Temperatur erhöht. Für eine genauere Analyse ist es sinnvoll die Messwerte in ein Schaubild eingetragen. Hierzu wird das Volumen in Abhängigkeit der Temperatur (in °C) aufgetragen.

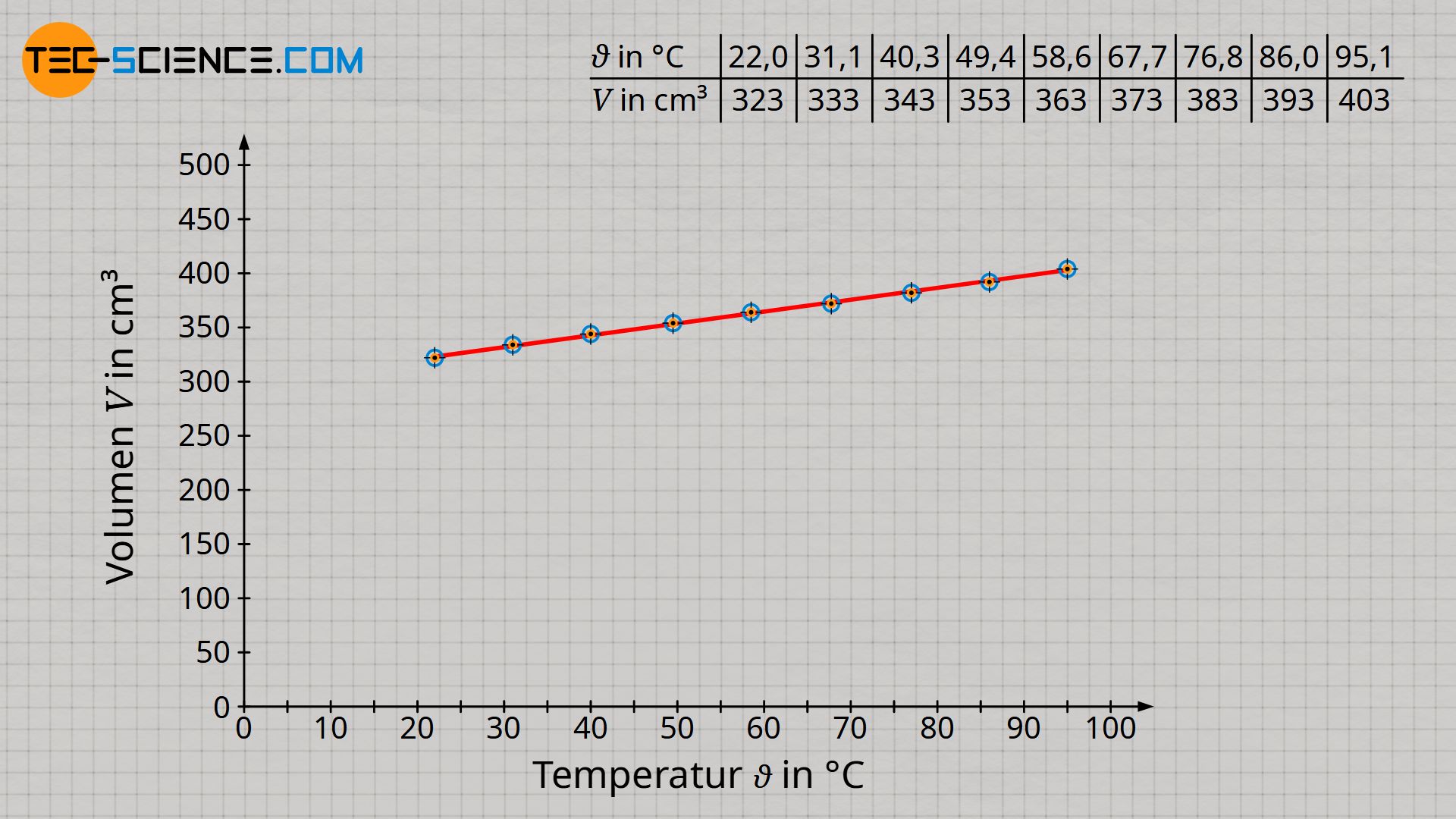
Es zeigt sich nach Auswertung des Versuchs im Diagramm ein linearer Zusammenhang zwischen der Gastemperatur und dem Gasvolumen. Dabei handelt es sich allerdings nicht um eine Proportionalität zwischen diesen Größen! Denn Proportionalität bedeutet, dass bspw. eine Verdopplung des Wertes einer Größe zur Verdopplung des Wertes einer anderen Größe führt.

Eine solche Proportionalität ist bei den vorliegenden Größen jedoch nicht gegeben! Zum Beispiel beträgt das Gasvolumen bei einer Temperatur von 22 °C rund 323 cm³. Bei etwa der doppelten Temperatur von 40,3 °C hat sich das Gasvolumen mit 343 cm² jedoch bei Weitem nicht im selben Maße verdoppelt, sondern hat sich lediglich um 6 % auf 343 cm³ ausgedehnt. Es ist folglich keine Proportionalität zwischen der Temperatur in °C und dem Volumen gegeben!

Proportionalität zwischen Volumen und Temperatur (Einheit: Kelvin)

Eine tatsächliche Proportionalität zwischen Volumen und Temperatur zeigt sich erst dann, wenn die Temperatur in der Einheit Kelvin und nicht in °C angegeben wird! Die in der Einheit Kelvin erhaltene Proportionalität ist nicht etwa zufällig. Auf dem oben beschriebenen Versuchsprinzip des Gasthermometers gründet überhaupt erst die Kelvinskala (siehe hierzu den Artikel Temperaturskalen). 

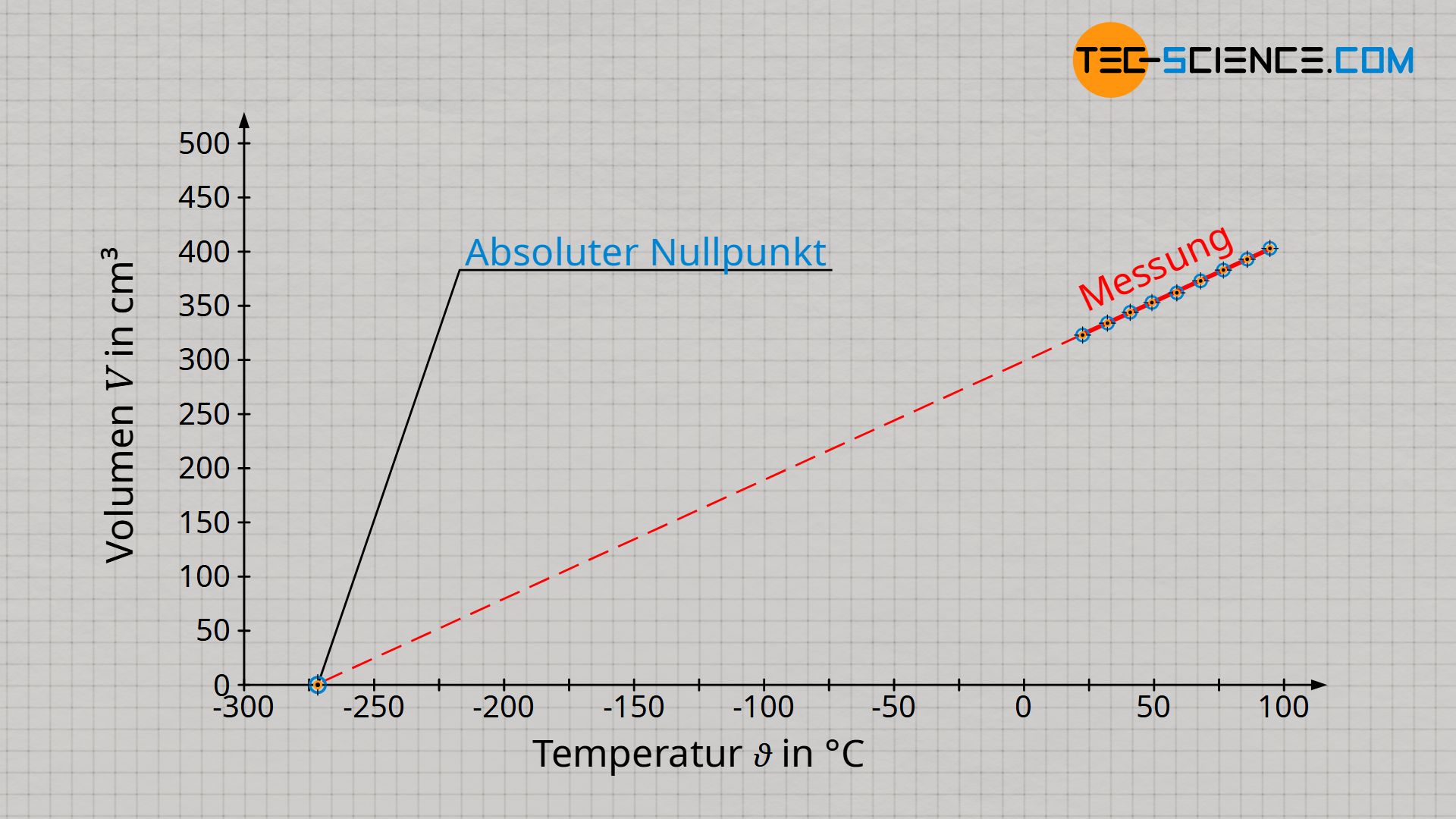
Der Absolute Nullpunkt ist dadurch definiert, dass sich die Teilchen nicht mehr bewegen. Die Teilchen fallen sozusagen „in sich zusammen“ und das Gas besitzt folglich keine Ausdehnung mehr (beachte, dass die Teilchen von idealen Gasen als Massepunkte betrachtet werden und somit selbst keine Ausdehnung haben). Das Gasvolumen ist im Absoluten Nullpunkt folglich null. Dieser Bewegungsnullpunkt oder Volumennullpunkt wurde zum Referenzpunkt der Kelvinskala (0 K = -273 °C).

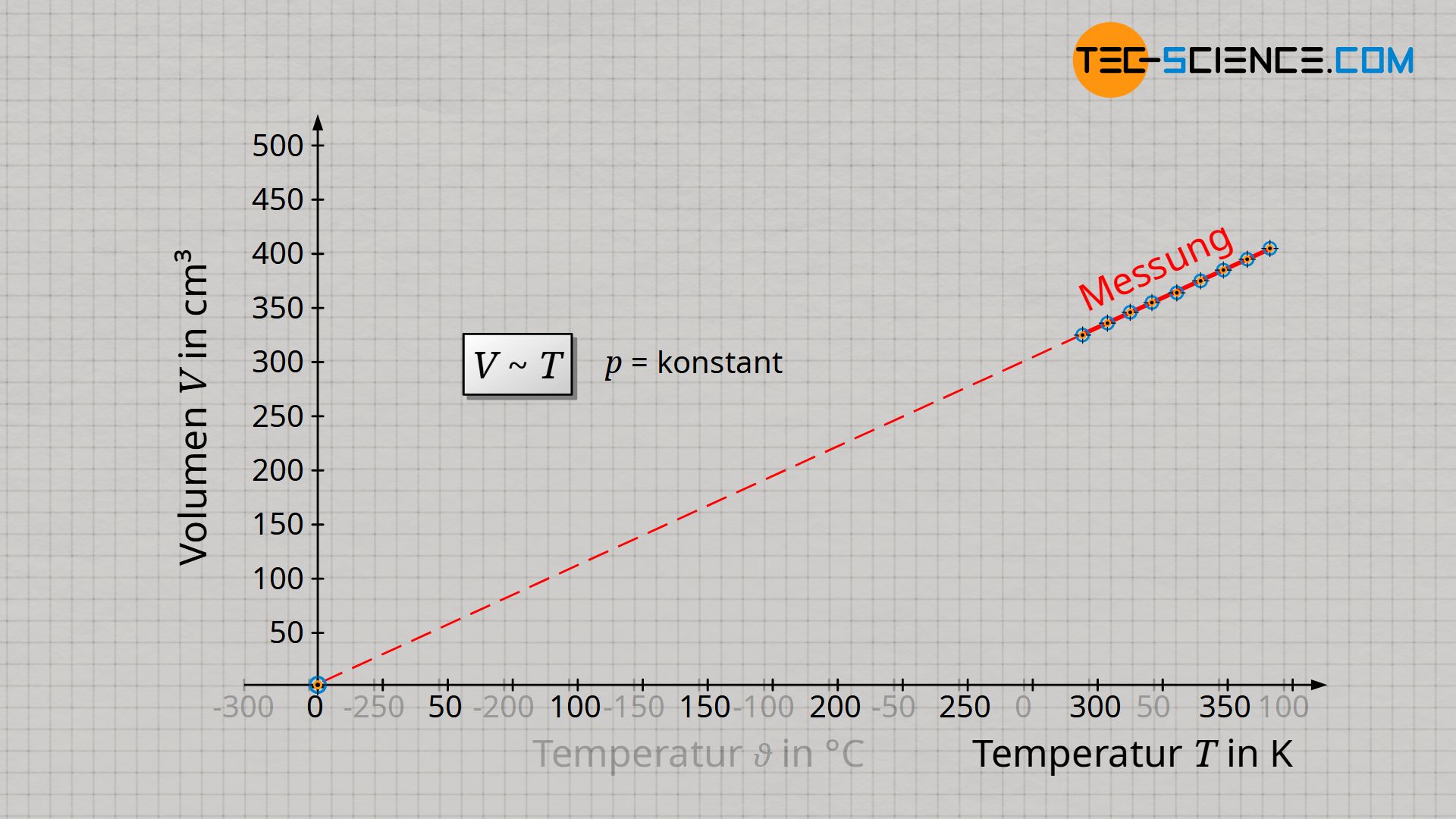
Vom Absoluten Nullpunkt aus betrachtet, steigt das Gasvolumen somit nur in der Einheit Kelvin proportional mit der Temperatur an. Beachte, dass sich immer nur dann ein proportionaler Zusammenhang zwischen zwei Größen ergibt, wenn sich deren Veranschaulichung im Diagramm durch eine Ursprungsgerade darstellen lässt. Nur wenn man also die Temperatur in der Einheit Kelvin angibt, gilt ein proportionaler Zusammenhang zwischen Volumen und Temperatur:

\begin{align}
&\boxed{V \sim T} ~~~~~ \text{isobare Zustandsänderung eines geschlossenen Systems} \\[5px]
\end{align}

Folgerung

Wenn sich bei einem proportionalen Verhalten zweier Größen, die eine Größe im selben Maße verändert wie die andere Größe, dann ist der Quotient aus beiden Größen offenbar stets konstant. Dies Aussage kann auch anhand der Wertetabelle rasch verifiziert werden.

Temperatur ϑ in °C	22,0	31,1	40,3	49,4	58,6	67,7	76,8	86,0	95,1
Temperatur T in K	295,2	304,3	313,4	322,6	331,7	340,8	350,0	359,1	368,3
Volumen V in cm³	323	333	343	353	363	373	383	393	403
V/T in cm³/K	0,91	0,91	0,91	0,91	0,91	0,91	0,91	0,91	0,91

\begin{align}
&\boxed{ \frac{V}{T}= \text{konstant}}~~~~~\text{Gesetz von Gay-Lussac} \\[5px]
\end{align}

Die Konstanz des Quotienten von Volumen und Temperatur bei einem isobaren Prozess wurde unter anderem von dem Physiker Joseph Louis Gay-Lussac experimentell untersucht. Deshalb ist diese Gesetzmäßigkeit als Gay-Lussac’sches Gesetz bekannt.

Das Gesetz von Gay-Lussac besagt, dass bei einer isobaren Zustandsänderung eines geschlossenen Systems, der Quotient von Volumen und Temperatur konstant ist!

Verknüpfung zweier Zustände

Bei einem isobaren Prozess hat also der Quotient von Volumen und Temperatur für alle Gaszustände denselben konstanten Wert. Deshalb gilt insbesondere, dass der Quotient von Volumen und Temperatur in einem beliebigen (Anfangs-)Zustand 1 auch dem Quotienten von Volumen und Temperatur in einem beliebigen (End-)Zustand 2 entspricht:

\begin{align}
&\frac{V_1}{T_1} =\text{konstant}= \frac{V_2}{T_2} \\[5px]
&\boxed{\frac{V_1}{T_1} = \frac{V_2}{T_2}} \\[5px]
\end{align}

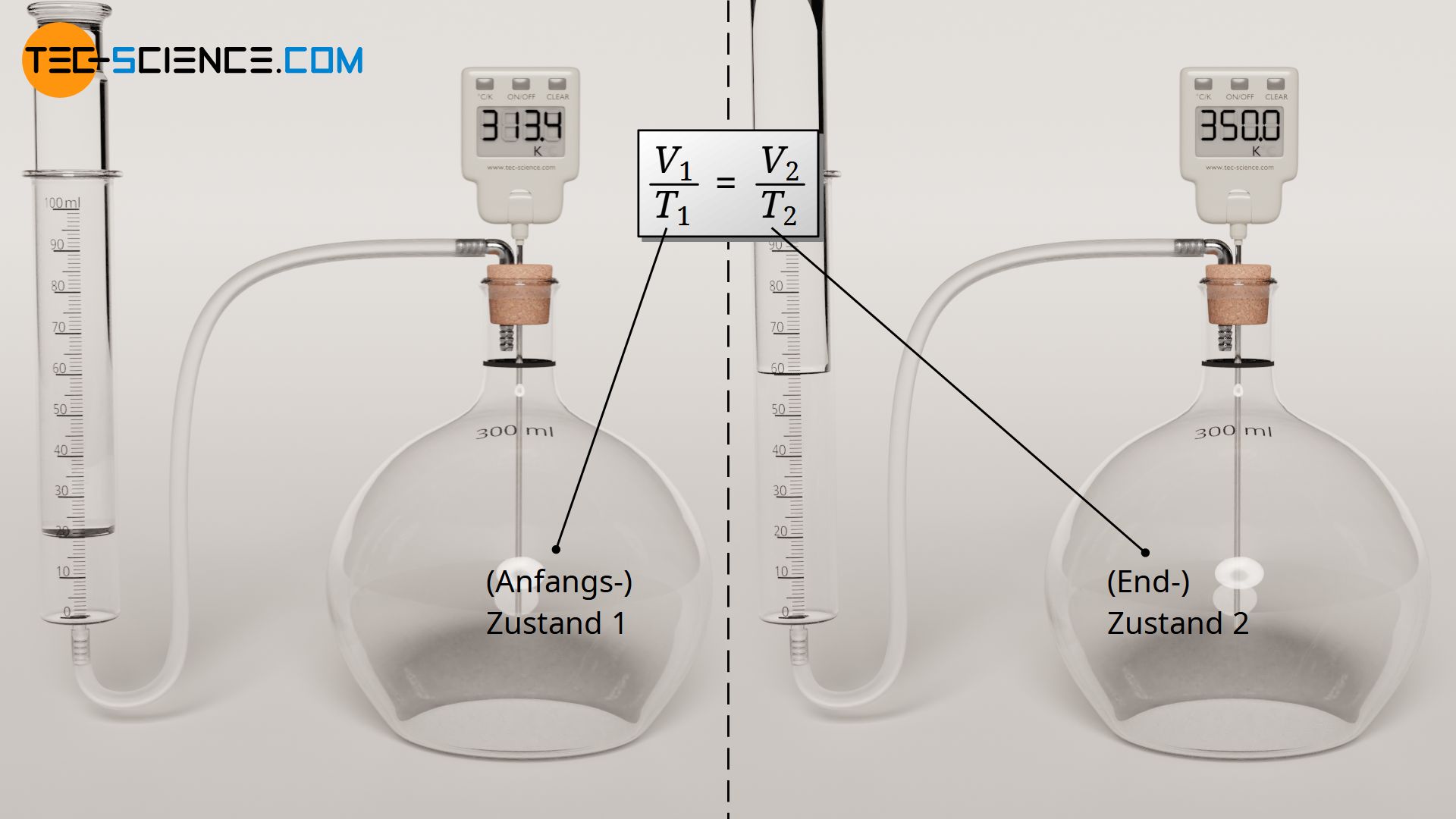
Bei einer isobaren Zustandsänderung eines geschlossenen Systems, stehen zwei Zustände über den Quotienten von Volumen und Temperatur in Zusammenhang!

Zusammenhang zum idealen Gasgesetz

Der oben gezeigte Zusammenhang zwischen zwei Gaszuständen ergibt sich auch aus dem idealen Gasgesetz für den Spezialfall einer Zustandsänderung bei konstantem Druck (p₁=p₂):

\begin{align}
\require{cancel}
&\frac{\cancel{p_1} \cdot V_1}{T_1} = \frac{\cancel{p_2} \cdot V_2}{T_2} \\[5px]
&\boxed{\frac{V_1}{T_1} = \frac{V_2}{T_2} } \\[5px]
\end{align}

Die Konstanz des Quotienten aus Volumen und Temperatur ergibt sich auch direkt anhand der thermischen Zustandsgleichung. Für den Fall, dass sich der Druck nicht ändert (p=konstant) und das System geschlossen ist (m=konstant) gilt:

\begin{align}
&\boxed{p \cdot V = R_\text{s} \cdot m \cdot T} ~~~~~\text{thermische Zustandsgleichung}\\[5px]
&\frac{V}{T} = \underbrace{R_\text{s} \cdot \frac{m}{p}}_{=\text{konstant}} \\[5px]
&\boxed{\frac{V}{T} =\text{konstant}} \\[5px]
\end{align}