Als Magnus-Effekt bezeichnet man die seitlich wirkende Kraft auf rotierende runde Körper in einer Strömung!
Einleitung
Jeder der schon einmal Fußball gespielt hat, hat sehr wahrscheinlich mit dem Magnus-Effekt bereits zu tun gehabt. Die Bananenflanke beim Freistoß ist ein Resultat hiervon. Gibt man dem Ball beim Schuss eine Rotation mit (Drall oder Effet genannt), dann bewegt sich dieser auf einer gekrümmten Bahn. Die Richtung, in die der Ball abgelenkt wird, entspricht der Richtung des mitgegebenen Dralls.
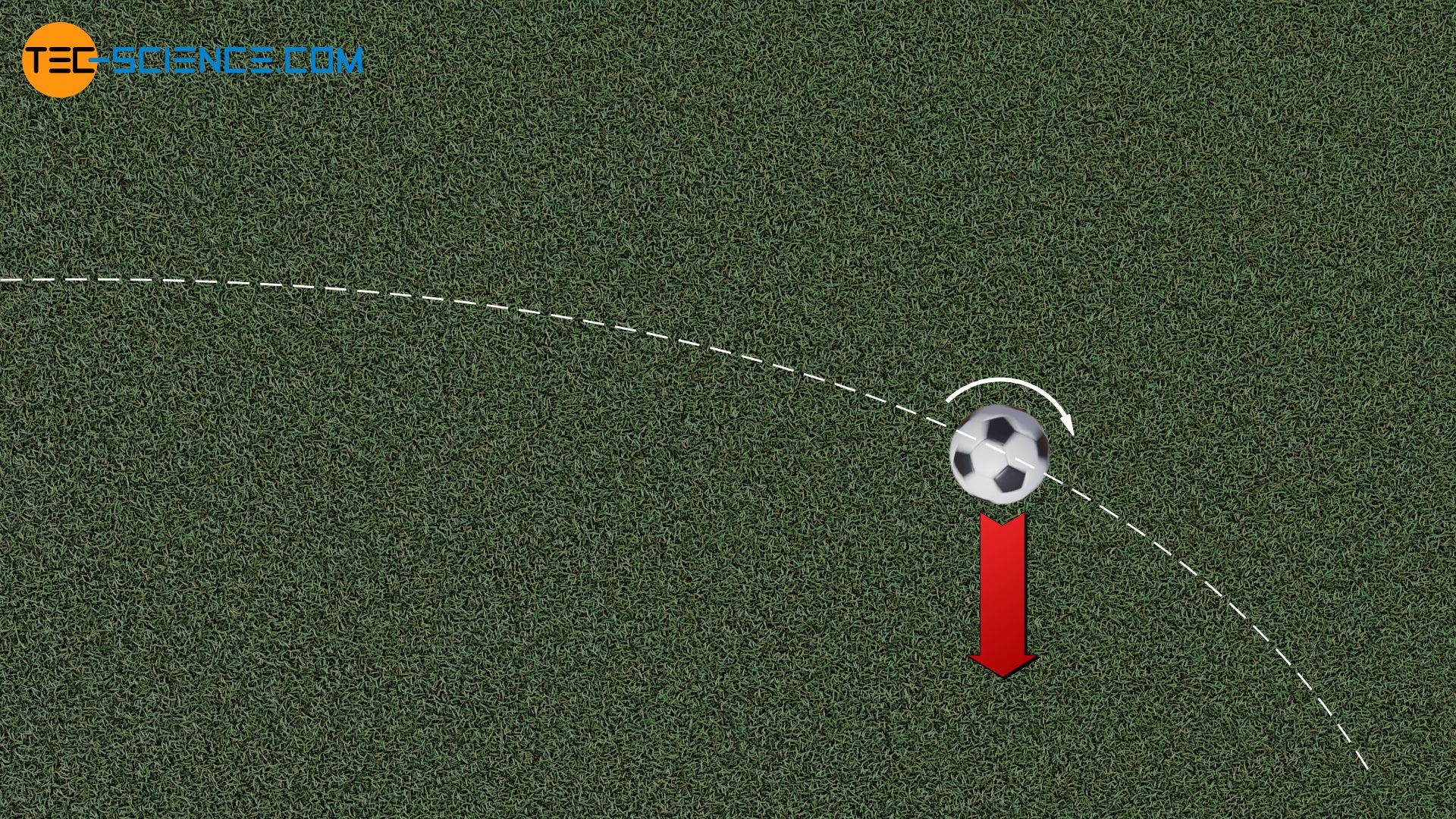
Als Magnus-Effekt bezeichnet man die von einer Strömung ausgeübte seitliche Kraft auf einen rotierenden runden Körper!
Nicht nur beim Fußballspielen wird der Magnus-Effekt genutzt, sondern auch beim Tennisspielen. Dort wird er bspw. beim Topspin verwendet. Der Topspin sorgt dafür, dass der Ball nach dem Überqueren des Netzes möglichst rasch nach unten fällt. Das Gegenstück zum Topspin ist der Slice, der ebenfalls auf dem Magnus-Effekt beruht. In der Technik findet der Magnus-Effekt in Form von Flettner-Rotoren Anwendung (später mehr dazu).
Überlagerung zweier Bewegungen
Wie kommt es nun zu einer solchen ablenkenden Kraft. Hierzu betrachten wir die Strömungsverhältnisse um einen umströmten, rotierenden Zylinder genauer. Beachte, dass es aus strömungstechnischer Sicht dabei keine Rolle spielt, ob sich ein Körper in einem ruhenden Fluid bewegt (bspw. ein fliegender Fußball in ruhender Luft) oder ein ortsfester Körper von einem bewegten Fluid umströmt wird (z.B. ein ruhender Fußball im Wind). Entscheidend ist lediglich die Relativgeschwindigkeit zwischen Körper und Fluid.
Die sich um den bewegten rotierenden Zylinder bildende Strömung, resultiert letztlich aus zwei überlagerten Strömungen:
- Strömung eines nicht-rotierenden Zylinders in einem hierzu bewegten Fluid
- Strömung eines ortsfest rotierenden Zylinders in einem ruhenden Fluid
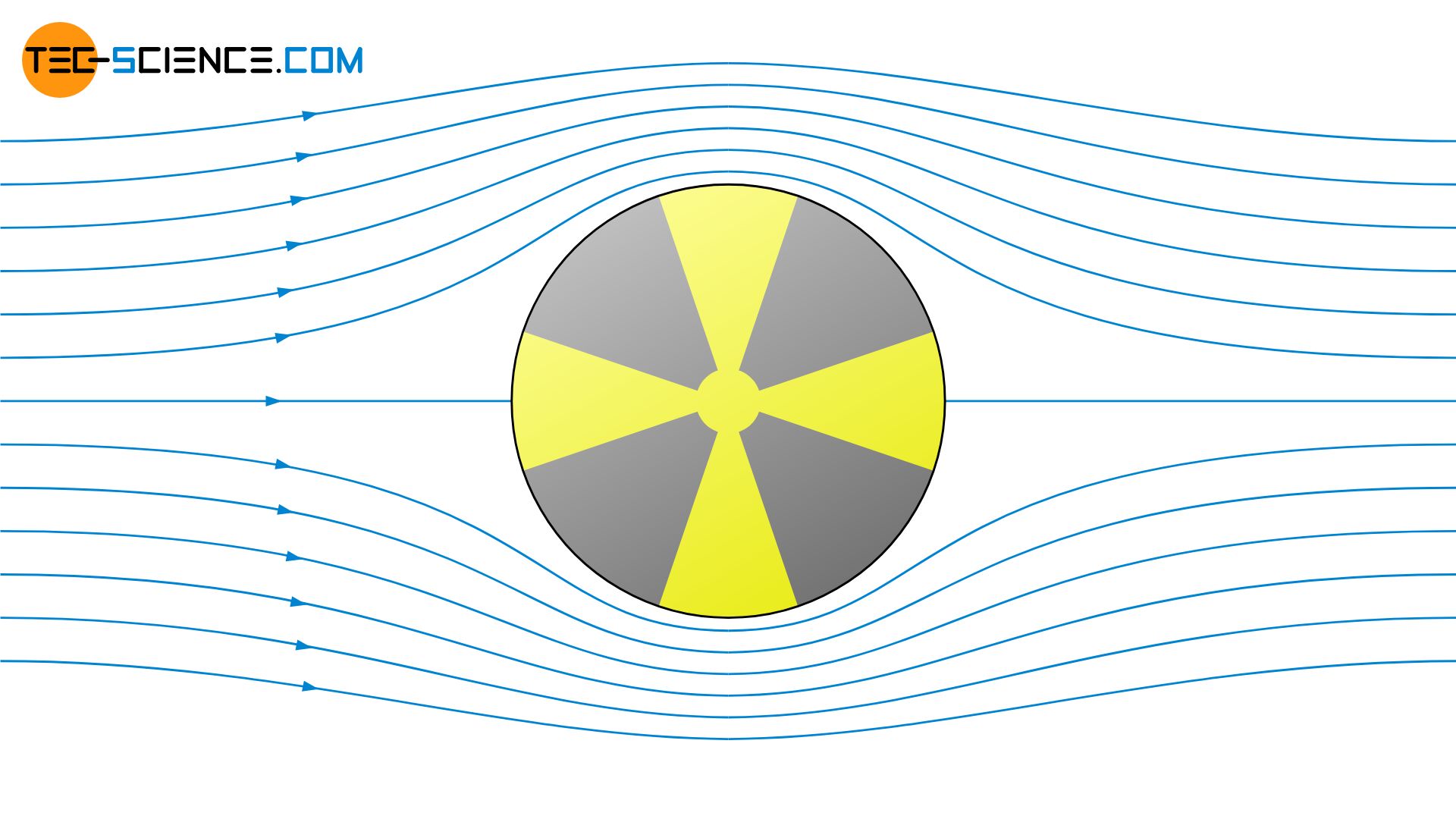
Der Einfachheit halber gehen wir von einer vollständig laminaren Umströmung des Zylinders unter Vernachlässigung der Reibung aus (Potentialströmung). Rotiert der Zylinder nicht, so erhält man eine symmetrische Umströmung des Zylinders. Die Stromlinien werden nach unten und oben gleichermaßen verdrängt. Anschaulich zeigt sich anhand der dichter verlaufenden Stromlinien eine Zunahme der Strömungsgeschwindigkeit (siehe hierzu auch Artikel Stromlinien, Bahnlinien, Streichlinien und Zeitlinien). Physikalisch ist dies mit der Erhaltung der Masse begründet. Eine Verengung des Strömungsquerschnitts bedeutet unweigerlich eine Zunahme der Strömungsgeschwindigkeit, da nach wie vor dieselbe Masse durch den betrachteten Querschnitt strömen muss.
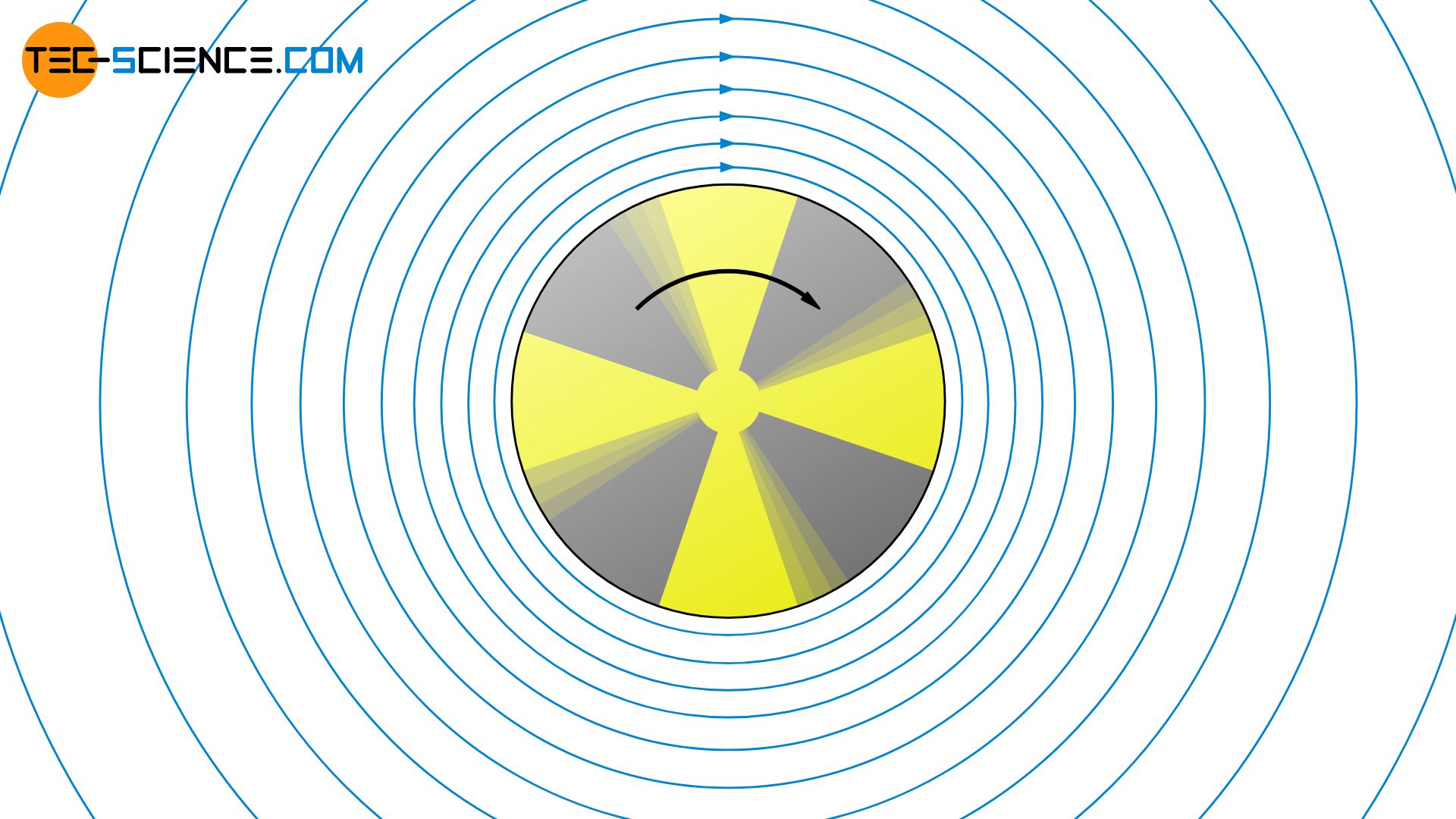
Nun betrachten wir das Strömungsfeld eines ortsfest rotierenden Zylinders in einem ruhenden Fluid. Die unmittelbar am Zylinder befindlichen Fluidteilchen haften dort an der Wand aufgrund der wirkenden Adhäsionskräfte (Haftbedingung). Die Fluidteilchen rotieren dort mit derselben Geschwindigkeit wie der Zylinder. Die Fluidteilchen über je nach Viskosität des Fluids aber auch Kräfte auf die umliegenden konzentrischen Fluidschichten aus. Diese werden somit mit in Rotation versetzt. Es bildet sich eine sogenannten Zirkulationsströmung aus.
Erklärung durch den Bernoulli-Effekt
Überlagert man nun die beiden oben genannten Strömungsfelder, so erhält man das Strömungsbild, wenn der Zylinder rotiert und gleichzeitig umströmt wird. In diesem Fall ist die Umströmung nicht mehr symmetrisch. Im oberen Bereich rotiert der Zylinder mit der Strömungsrichtung. Die Fluidteilchen werden hierdurch zusätzlich beschleunigt. Im unteren Bereich ist die Rotationsbewegung hingegen entgegen der Strömungsrichtung gerichtet. Die Fluidteilchen werden hierdurch abgebremst. Die Strömungsgeschwindigkeit ist also im Bereich wo die Rotation mit der Umströmung gerichtet ist, größer als im Bereich wo der Zylinder entgegen der Strömung rotiert.
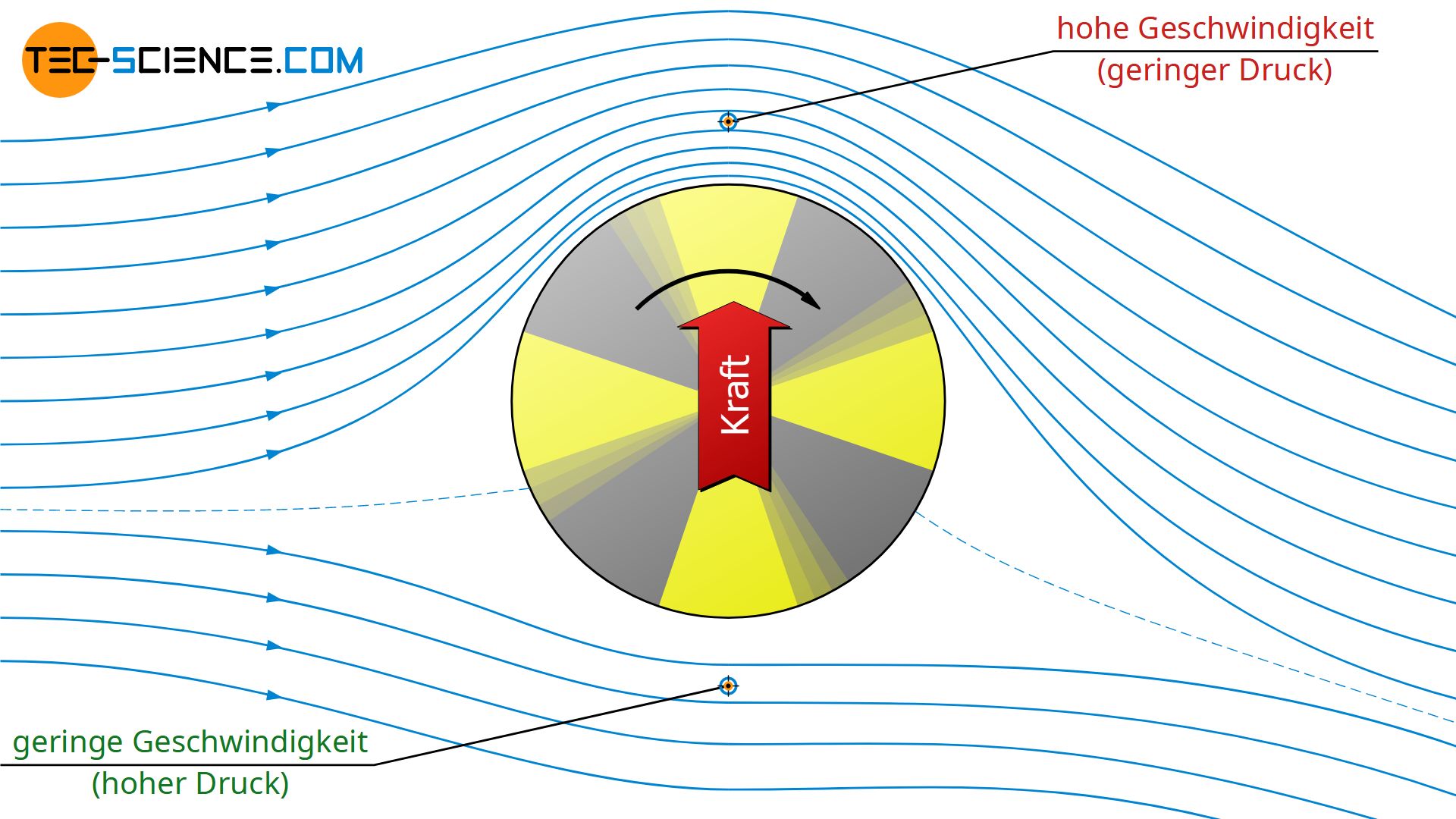
Gemäß der Bernoulli-Gleichung sind mit den unterschiedlichen Strömungsgeschwindigkeiten aber auch unterschiedliche Drücke verbunden. Dabei gilt: umso höher die Strömungsgeschwindigkeit, desto geringer der Druck (Bernoulli-Effekt). Im Strömungsbereich, der mit der Rotation des Zylinders gerichtet ist, ist der Druck folglich geringer als im gegenüberliegenden Strömungsbereich. Insgesamt wirkt damit auf den rotierenden Zylinder eine seitlich (bzgl. der Strömungsrichtung) ablenkende Kraft. Dies ist der Magnus-Effekt.
Erklärung durch die Grenzschichtablösung
Tatsächlich spielt für den Magnus-Effekt auch die Strömungsablösung (Grenzschichtablösung) eine Rolle. In der Realität wird ein runder oder zylindrischer Körper nicht vollständig laminar umströmt. Aufgrund der Verzögerung des Fluids nach Passieren der dicksten Stelle des Zylinders (Aufweitung der Stromlinien!), steigt der Druck gemäß der Bernoulli-Gleichung wieder an. Dieser Druckanstieg bewirkt in der Grenzschicht eine Rückströmung des Fluids. In der Folge löst sich die Strömung vom Zylinder ab.
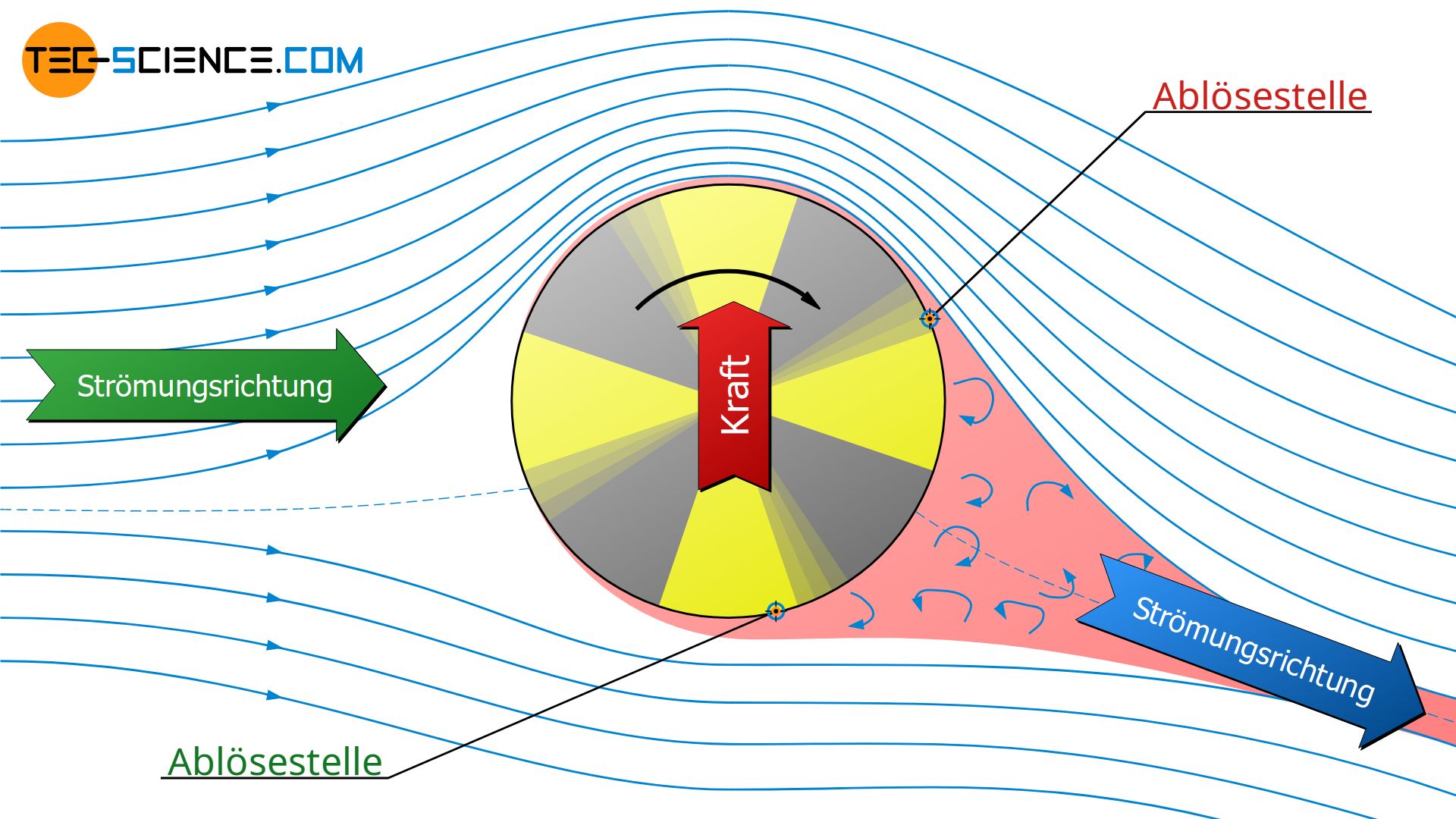
Durch die Rotation des Zylinders ist nun aber die Strömungsgeschwindigkeit auf der mit der Strömung rotierenden Seite größer. Die höhere kinetische Energie führt dazu, dass die Strömung dem Zylinder trotz des Druckanstiegs länger folgen kann. Der Zylinder wird folglich länger umströmt und die Grenzschichtablösung tritt somit erst später am Zylinder auf. Die Strömungsablösung erfolgt also nicht mehr symmetrisch, sondern verschiebt sich auf jene Seite, die entgegen der Strömung rotiert.
Das Fluid wird bei der Umströmung folglich schräg abgelenkt. Offensichtlich verleiht der rotierenden Zylinder der Strömung einen zusätzlichen seitlichen Impuls, der die Folge einer Kraft sein muss. Gemäß des dritten Newtonschen Axioms (Aktion=Reaktion) bedeutet dies im Umkehrschluss aber, dass auch eine seitliche Kraft von der Strömung auf den Zylinder ausgeübt wird. Der Magnus-Effekt.
Flettner-Rotor
Die technische Anwendung des Magnus-Effekts findet man bspw. bei sogenannten Flettner-Rotoren. Diese wurden/werden in der Schifffahrt verwendet und bestehen im Wesentlichen aus rotierenden Zylindern, die senkrecht stehen. Diese Zylinder werden durch Elektromotoren angetrieben. Vom Wind umströmt, erzeugen die rotierenden Zylinder gemäß des Magnus-Effektes eine entsprechende Kraft, die als Vortrieb dient. Die antreibende Kraft ergibt dabei aus der Summe der Kraft des Magnus-Effekts und der Luftwiderstandskraft.







