A Prandtl tube is used to measure the dynamic pressure. From this, the flow speed relative to the tube can be determined.
Stagnation pressure and stagnation point
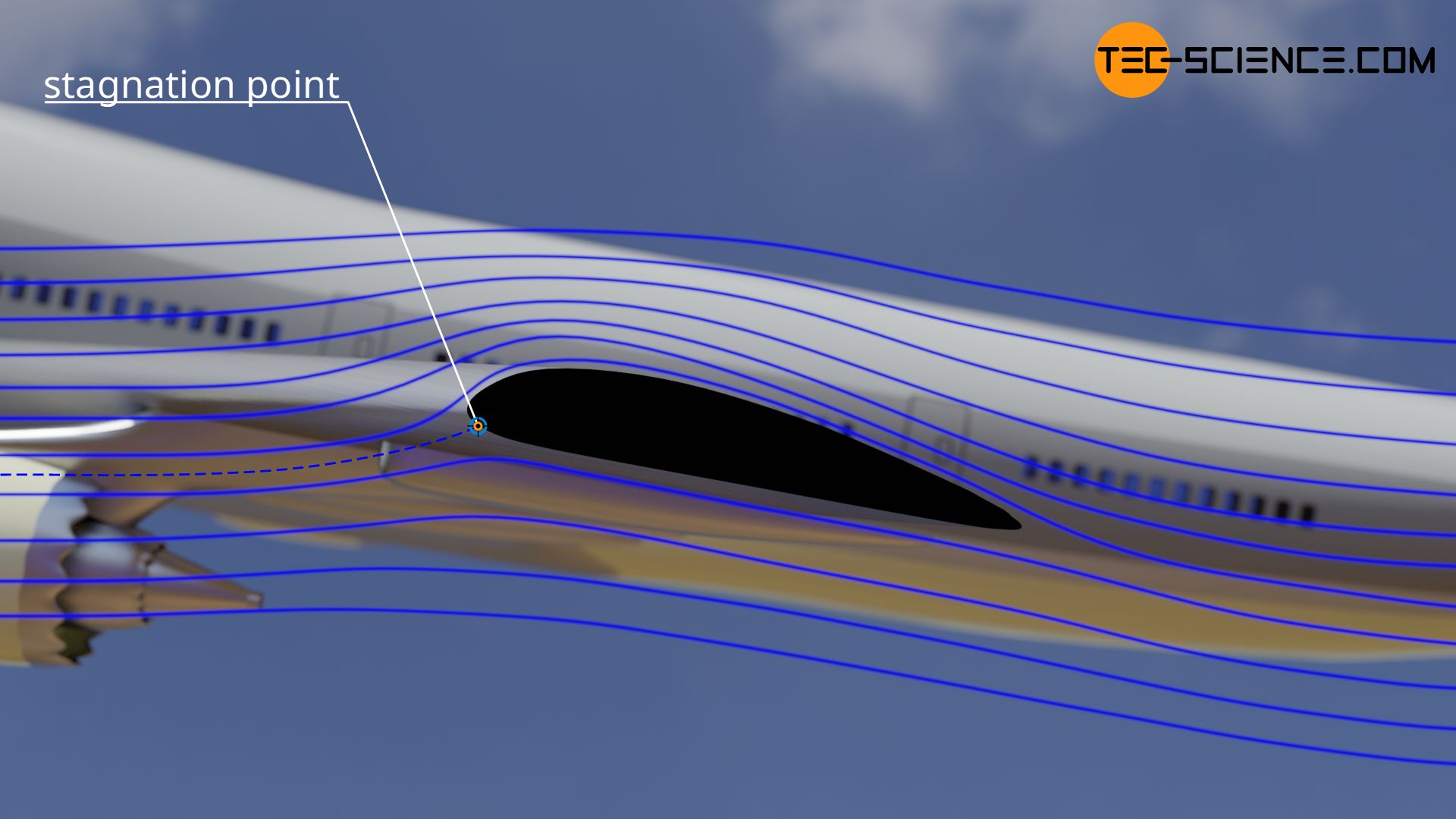
If a flow hits a plate or other object, the fluid is obviously slowed down. This process is associated with an increase in pressure, as the dynamic pressure (linked to the kinetic energy) is converted into static pressure. The measured total pressure when the fluid is stagnating on an object is referred to as stagnation pressure. The point at which the fluid comes to a standstill on an object is called stagnation point.
The total pressure (= static pressure of the flow + dynamic pressure of the flow) that results when a fluid is decelerated to a standstill at a so-called stagnation point is also known as stagnation pressure!
Graphically, the stagnation point is located where a streamline hits the surface of the object perpendicularly and is thus (theoretically) completely slowed down. In practice, due to Brownian motion, the fluid particles will sooner or later diffuse out of the stagnation point and be accelerated around the object again. On a microscopic level, the accumulation of fluid particles in the stagnation point is thus only of short duration.
Since the dynamic pressure is directly linked to the kinetic energy and thus the flow velocity, the flow velocity can be deduced by measuring the dynamic pressure. The flow speed is to be considered relative, because one can also move an object through a resting fluid. The measured dynamic pressure then corresponds to the speed of the object relative to the fluid. This principle is used in airplanes, helicopters or even racing cars to measure the speed in relation to the surrounding air (airspeed indicator).
From the general relationship between total pressure ptot, static pressure psta and dynamic pressure pdyn, the following formula for the flow velocity results:
\begin{align}
&p_\text{tot} = p_\text{sta} + p_\text{dyn} \\[5px]
&p_\text{tot} = p_\text{sta} + \frac{1}{2} \rho \cdot v^2 \\[5px]
&\boxed{v=\sqrt{\frac{2\left(p_\text{tot}-p_\text{sta}\right)}{\rho}}} \\[5px]
\end{align}
Measuring dynamic pressure
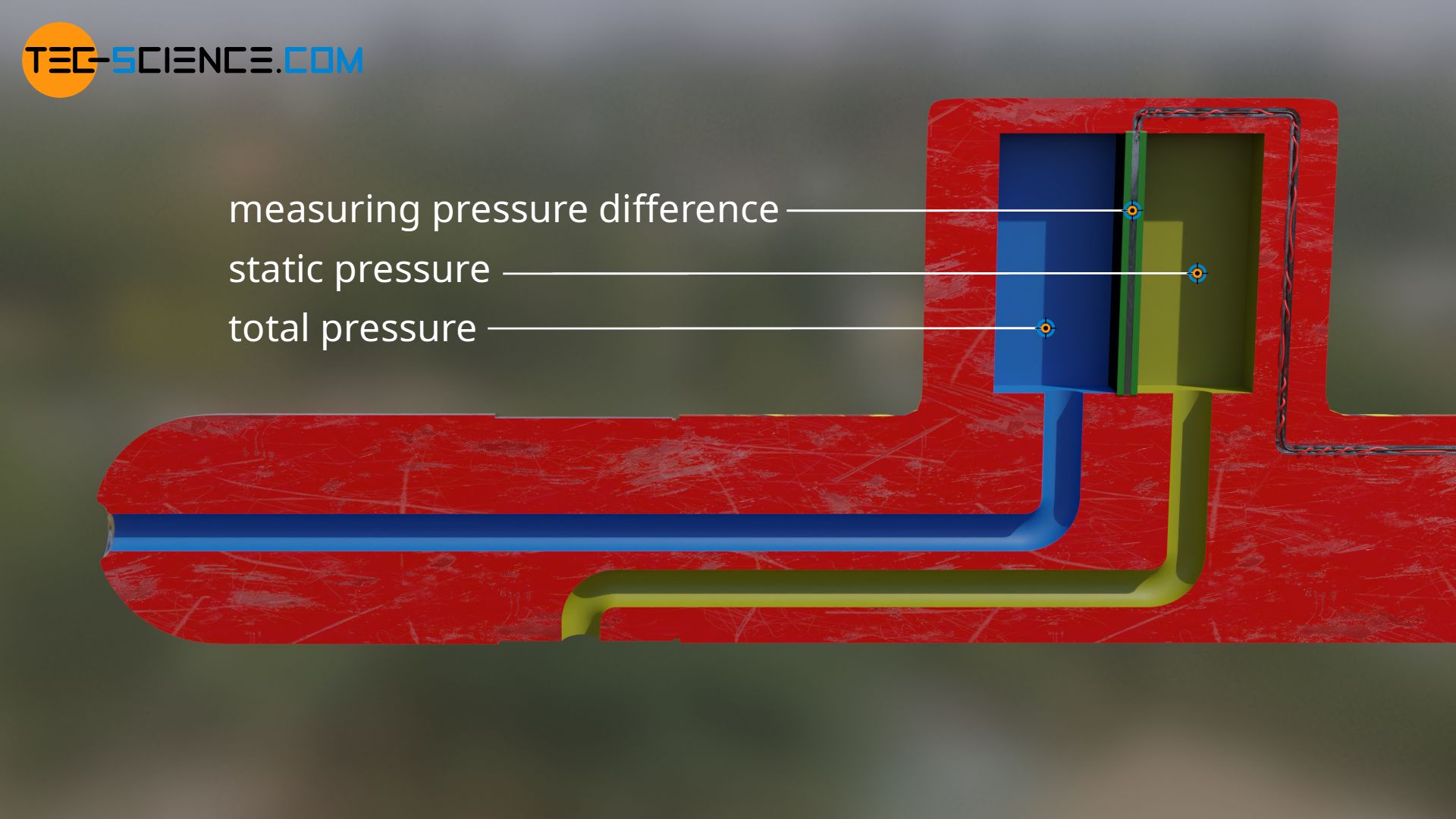
To determine the dynamic pressure, first the total pressure (stagnation pressure) at the stagnation point is measured, i.e. the static pressure which is present after the fluid has been completely decelerated. This static pressure in resting air must not be confused with static pressure in freestream! For this purpose, only a pipe open on one side is held in the flowing air. In the pipe, the fluid decelerates until it comes to a standstill (stagnation point). The pressure present there thus corresponds to the total pressure or stagnation pressure. Such a pipe for measuring the total pressure is also called a Pitot tube.
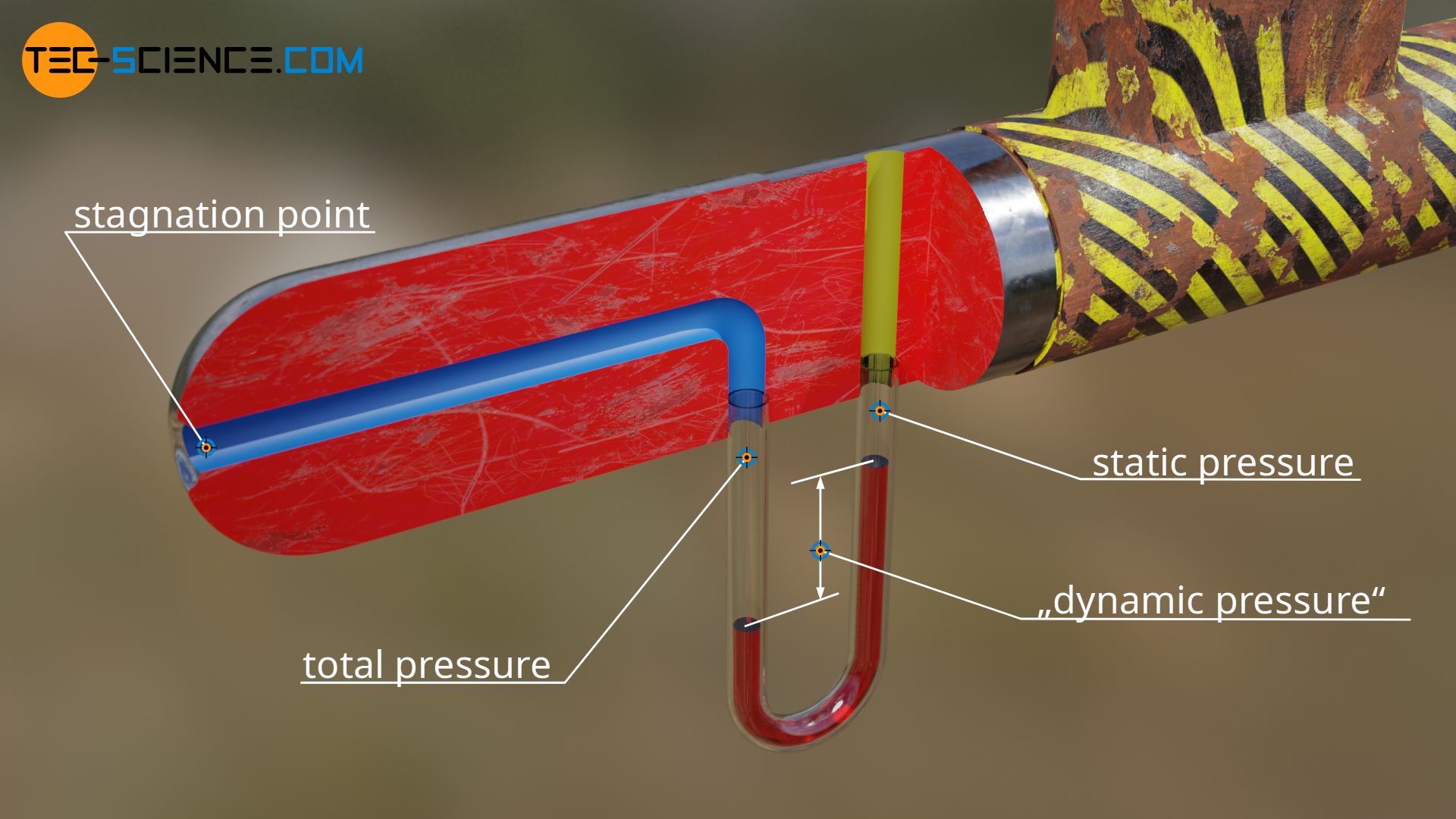
To determine the dynamic pressure in the airstream, the static pressure in the flowing fluid must now be subtracted from the total pressure. This pressure difference can be physically generated and even made visible. A U-pipe filled with liquid can be used for this purpose. One side is connected to the pitot tube. The opening of the other side is placed perpendicular to the flowing fluid. So the fluid above the opening is not decelerated and thus imposes only static pressure.
Two pressures now act on the liquid in the U-tube. On the one hand the total pressure of the decelerated air (Pitot tube) and on the other hand the lower static pressure of the flowing air. The difference of both pressures lifts the liquid upwards. The height difference in the liquid level is therefore a measure of the pressure difference and thus of the dynamic pressure or flow velocity! The Pitot tube and the U-tube thus form the overall unit for measuring dynamic pressure. Such a probe is also called a Prandtl tube.
A Prandtl tube serves as a dynamic pressure probe to measure the dynamic pressure and thus the flow velocity!
Instead of a U-tube, in today’s Prandtl tubes the channels for static pressure measurement are incorporated directly into the probe. A pressure sensor separates the total pressure in a chamber from the static pressure. The output measuring signal of the sensor thus corresponds to the pressure difference and is a direct measure of the dynamic pressure or flow velocity.