Druckverlust in Rohrsystemen (Rohrreibungszahl)

Druckverluste in Rohrleitungen entstehen durch Reibungseffekte im Fluid (Viskosität) und zwischen Fluid und Wand. Zudem entstehen in einzelnen Bauteilen Druckverluste.

Einleitung

Strömen Fluide durch Rohre, dann treten unweigerlich Energieverluste auf. Dies ist zum einen durch Reibung begründet, die zwischen Rohrwand und Fluid entsteht (Wandreibung). Zum anderen entstehen auch innerhalb des Fluids Reibungseffekte aufgrund der Viskosität des Fluids (innere Reibung). Dieser innere Reibungseffekt ist umso größer, je schneller das Fluid strömt (siehe hierzu auch Artikel Hagen-Poiseuille-Gesetz für Rohrströmungen mit Reibung).

Weitere Strömungsverluste entstehen durch Verwirbelungen im Fluid, die besonders an Armaturen hervorgerufen werden, die letztlich Strömungshindernisse darstellen. Diese Verwirbelungen beinhalten zwar kinetische Energien, transportieren sie aber makroskopisch betrachtet nicht durch die Rohrleitung, sondern verbleiben sozusagen an Ort und Stelle.

Im Artikel Bernoulli-Effekt wurde bereits ausführlich gezeigt, dass Druck auch als volumenspezifische Energie aufgefasst werden kann. In diesem Zusammenhang gibt der Druck an, wie viel Energie pro Volumeneinheit in einem Fluid steckt. Wenn salopp formuliert, Druck also Energie bedeutet, dann bedeutet ein Energieverlust unweigerlich einen Druckverlust. Die oben beschriebenen Reibungs- und Strömungseffekte sind somit stetes begleitet mit einem entsprechenden Druckverlust.

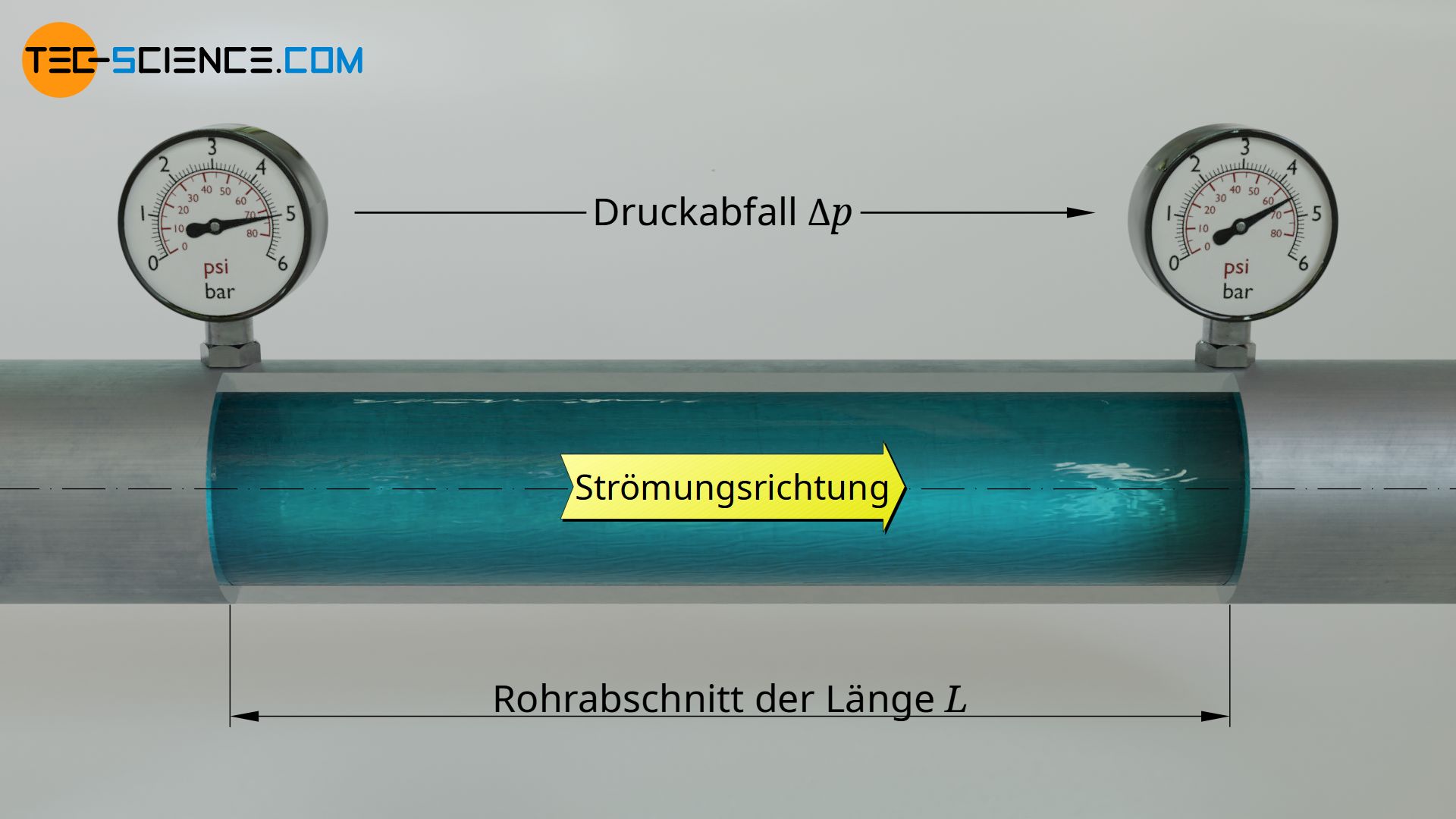
Der Druckverlust bezieht sich dabei grundsätzlich auf den Verlust an statischem Druck (bzw. Verlust am Gesamtdruck). Der dynamische und der hydrostatische Druck werden nicht durch die Energieverluste beeinflusst, da diese sozusagen nur Wirkung der Strömung sind aber nicht Ursache. Die hydrostatischen Drücke und dynamischen Drücke sind durch die Geometrie der Rohrleitung vorgegeben. Weitere Druckverluste entstehen in einzelnen Bauteilen, z.B. Ventile, Krümmer oder Messapparaturen.

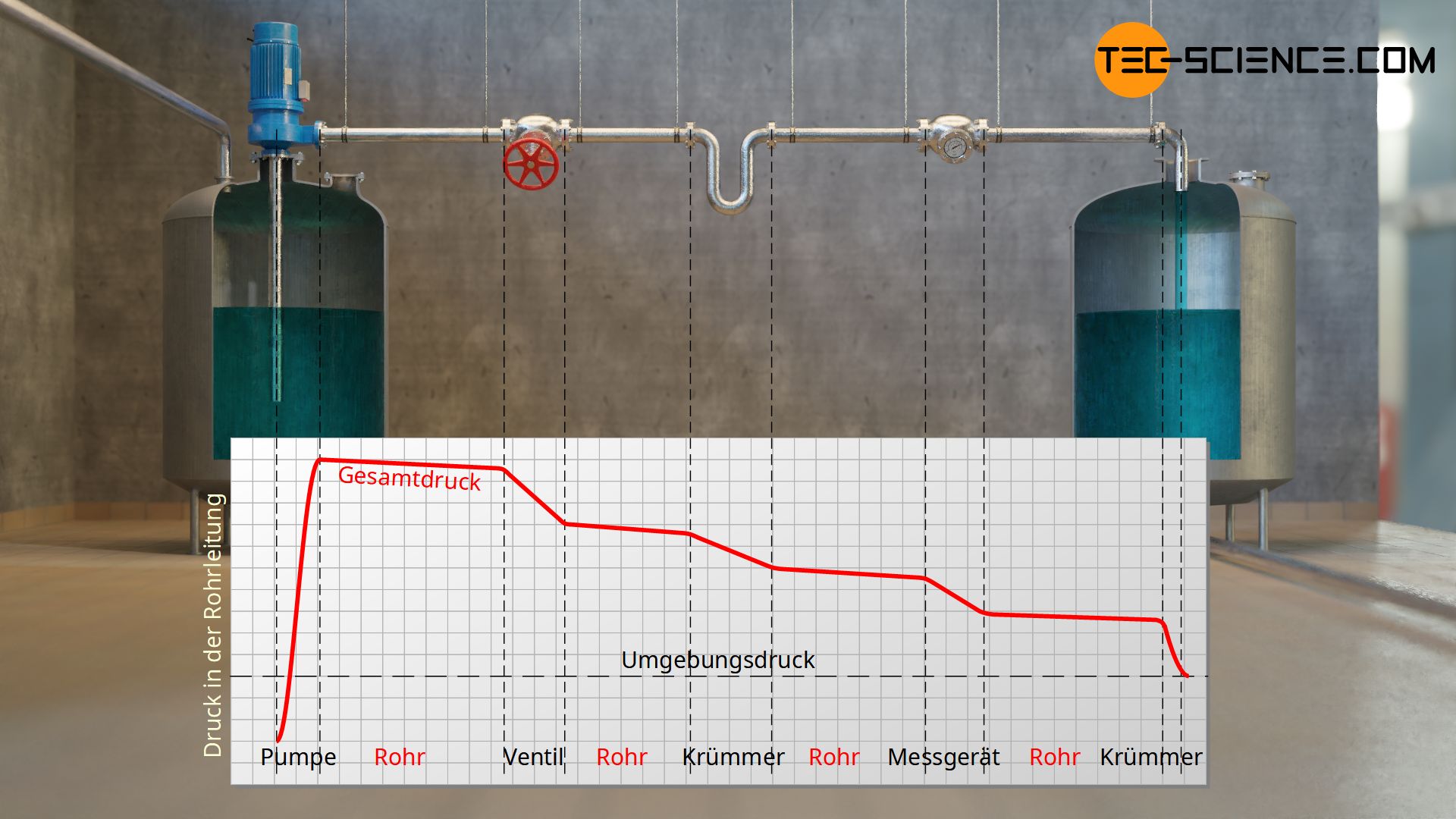
Der (statische) Druckverlust in Rohrleitungen ist mit dem Verlust an mechanischer Energie verbunden, der unweigerlich beim Strömen eines Fluids durch ein Rohrsystem auftritt.

Im Folgenden betrachten wir ausschließlich inkompressible Strömungen wie Flüssigkeiten oder langsam strömende Gase.

Druckverlust in Rohrleitungen (Rohrreibungszahl)

Unabhängig davon, ob es sich um eine laminare oder turbulente Strömung handelt, beschreibt man den Druckverlust durch eine Rohrleitung mit Hilfe einer dimensionslosen Ähnlichkeitskenngröße. Diese sogenannte Rohrreibungszahl λ beschreibt im Wesentlichen das Verhältnis zwischen Druckverlust Δp_V (Energieverlust) und der in der Strömung enthaltenen kinetischen Energie in Form des dynamischen Drucks Δp_dyn (Staudruck). Zudem muss das Verhältnis von Rohrinnendurchmesser d und Rohrlänge L berücksichtigt werden.

\begin{align}
& \lambda := \frac{\Delta p_\text{V}}{p_\text{dyn}} \cdot \frac{d}{L}~~~\text{mit}~~~ p_\text{dyn}=\tfrac{1}{2}\rho ~\bar v^2 ~~~\text{folgt:} \\[5px]
\label{lambda}
& \boxed{\lambda= \frac{\Delta p_\text{V}}{\tfrac{1}{2}\rho ~\bar v^2} \cdot \frac{d}{L}} ~~~\text{Rohrreibungszahl} \\[5px]
\end{align}

Darin bezeichnet d den Innendurchmesser des Rohres und L die Länge des geraden Rohrabschnitts, entlang dessen der Druckverlust Δp_V beträgt. Die Rohrreibungszahl wird auch als Rohrwiderstandszahl bezeichnet oder Rohreibungskoeffizient genannt.

Die Strömungsgeschwindigkeit bezieht sich dabei auf die mittlere Strömungsgeschwindigkeit im Rohr. Beachte, dass sowohl bei turbulenter als auch bei laminarer Strömung keine einheitliche Geschwindigkeit über den Rohrquerschnitt hinweg vorliegt, sondern ein typisches Geschwindigkeitsprofil (siehe Hagen-Poiseuille-Strömung).

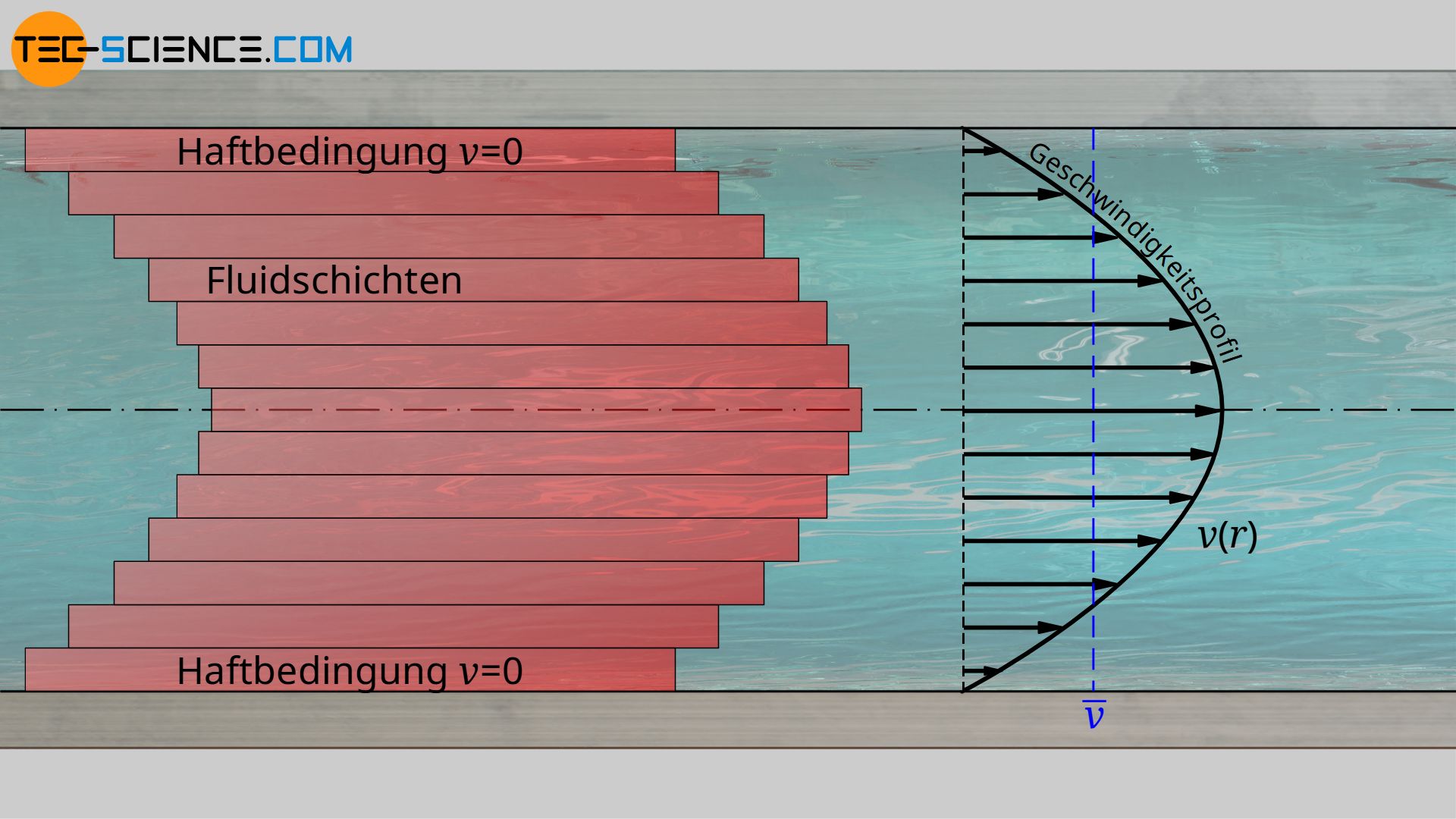
Der Rohrreibungskoeffizient (Rohrreibungszahl) ist eine dimensionslose Ähnlichkeitskenngröße zur Beschreibung des Druckverlustes in geraden Rohrabschnitten!

Anhand der Definition der Rohrreibungszahl als Ähnlichkeitskenngröße, kann man also in einem verkleinerten Modellmaßstab des späteren Rohrsystems zunächst die Rohrreibungszahl bestimmen. Anschließend kann man diese dann auf den realen Maßstab anwenden und somit den Druckverlust in der tatsächlichen Rohrleitung wie folgt bestimmen:

\begin{align}
\label{def}
& \boxed{\Delta p_\text{V} = \lambda \cdot \frac{1}{2}\rho ~\bar v^2 \cdot \frac{L}{ d}} ~~~\text{Druckverlust in einem geraden Rohrabschnitt} \\[5px]
\end{align}

Die Rohrreibungszahl lässt sich anhand der Geometrie des Rohres auch mathematisch berechnen wie sich später noch zeigen wird.

Beachte, dass diese Formel nur für gerade Rohrabschnitte gilt. In Rohrkrümmern treten aufgrund der Umlenkung der Strömung in der Regel weitere Strömungsverluste auf, die zu Druckverlusten führen. Diese bauteilabhängigen Druckverluste (Einzelwiderstände) werden durch einen Druckverlustbeiwert ζ gesondert berücksichtigt. Später mehr dazu.

In der Praxis wird häufig nicht eine bestimmte Strömungsgeschwindigkeit gefordert, sondern ein bestimmter Volumenstrom. Die mittlere Strömungsgeschwindigkeit ist dabei über die Querschnittsfläche des Rohres A mit dem Volumenstrom V* verknüpft:

\begin{align}
&\boxed{\dot V =\bar v \cdot A} ~~~\text{mit}~A=\frac{\pi}{4}d^2~~~\text{folgt:} \\[5px]
&\dot V = \bar v \cdot \frac{\pi}{4}~d^2 \\[5px]
\label{vol}
&\underline{\bar v = \frac{4\dot V}{\pi ~d^2}} \\[5px]
\end{align}

Wird Gleichung (\ref{vol}) in Gleichung (\ref{def}) eingesetzt, dann ergibt schließlich folgende Formel für den Druckverlust bei gegebenem Volumenstrom:

\begin{align}
& \Delta p_\text{V} = \lambda \cdot \frac{1}{2}\rho ~\left( \frac{4\dot V}{\pi ~d^2}\right)^2 \cdot \frac{L}{ d}\\[5px]
\label{volu}
& \boxed{\Delta p_\text{V} = \lambda \cdot \frac{8\rho~L}{\pi^2} \cdot \frac{\dot{V}^2}{d^5}} ~~~\text{Druckverlust in einem geraden Rohrabschnitt} \\[5px]
\end{align}

Der Durchmesser geht offensichtlich mit der fünften Potenz in die Berechnung des Druckverlustes ein und hat somit entscheidenden Einfluss. Im Allgemeinen gilt: umso größer der Durchmesser, desto geringer sind die Druckverluste! Beachte, dass die Rohrreibungszahl λ allerdings abhängig von Strömungsgeschwindigkeit ist. Die Strömungsgeschwindigkeit wiederum hängt vom Volumenstrom und somit vom vorhandenen Rohrdurchmesser ab! Diese Größen beeinflussen sich im Allgemeinen also gegenseitig.

Druckverlust bei laminarer Rohrströmung

Der aufgrund der Viskosität zustande kommende Druckverlust durch die innere Reibung des Fluids („Zähigkeit“) wurde für eine laminare Strömung bereits im Artikel zum Hagen-Poiseuille-Gesetz ausführlich hergeleitet:

\begin{align}
\label{lam}
& \boxed{\Delta p_\text{V,lam} = \frac{32~\eta ~ L}{d^2} \cdot \bar v} ~~~\text{Druckverlust durch Viskosität} \\[5px]
\label{lam2}
& \boxed{\Delta p_\text{V,lam} = \frac{128~\eta ~ L}{\pi d^4} \cdot \dot V} \\[5px]
\end{align}

Darin bezeichnet Δp_V,lam den Druckverlust entlang eines Rohrabschnitts mit dem Durchmesser d und der Länge L, wenn dieses von einem Fluid mit der dynamischen Viskosität η und der mittleren Geschwindigkeit v laminar durchströmt wird.

Der unweigerlich entstehende Druckverlust aufgrund der stets vorhandenen Viskosität von Fluiden, muss in jedem Fall kompensiert werden, wenn ein Fluid durch eine Rohrleitung gefördert werden soll. Der Druckverlust entspricht folglich dem Druck, den eine Pumpe in jedem Fall erzeugen muss, um das Fluid am Strömen zu halten.

Die Rohrreibungszahl λ_lam für eine laminare Rohrströmung lässt sich durch Einsetzen der Formel (\ref{lam}) in Gleichung (\ref{lambda}) ermitteln:

\begin{align}
\require{cancel}
\lambda_\text{lam} &= \frac{\Delta p_\text{V,lam}}{\tfrac{1}{2}\rho ~\bar v^2} \cdot \frac{d}{L}\\[5px]
&= \frac{\frac{32~\eta ~ L}{d^2} \cdot \bar v}{\tfrac{1}{2}\rho ~\bar v^2} \cdot \frac{d}{L}\\[5px]
&= \frac{2 \cdot 32~\eta ~ \cancel{L}~\cancel{\bar v}}{d^{\cancel{2}}~\rho ~\bar v^{\cancel{2}}} \cdot \frac{\cancel{d}}{\cancel{L}}\\[5px]
&= \frac{64~\eta}{d~\rho ~\bar v}\\[5px]
&= \dfrac{64}{\color{red}{\dfrac{d \rho ~\bar v}{\eta}}}~~~\text{mit}~~~\color{red}{Re=\frac{d~\rho~\bar v}{\eta}}\\[5px]
\end{align}

\begin{align}
\label{a}
&\boxed{\lambda_\text{lam}= \dfrac{64}{Re}} ~~~\text{Rohrreibungszahl bei laminarer Strömung}\\[5px]
\end{align}

Bei laminarer Strömung hängt die Rohrreibungszahl nur von der Reynoldszahl ab. Umso höher die Reynolds-Zahl, desto geringer die Rohrreibungszahl!

Beachte, dass die Rohrreibungszahl zwar mit zunehmender Strömungsgeschwindigkeit (zunehmender Reynoldszahl) abnimmt, dies aber nicht bedeutet, dass der Druckverlust hierdurch geringer wird. Der Druckverlust steigt gemäß Gleichung (\ref{def}) nämlich gleichzeitig quadratisch mit der Strömungsgeschwindigkeit an. Insgesamt nimmt der Druckverlust somit linear mit der Strömungsgeschwindigkeit zu – siehe Gleichung (\ref{lam})!

Es wurde bereits angedeutet, dass nicht nur innerhalb des Fluids selbst Reibung vorhanden ist, sondern im Allgemeinen auch zwischen Fluid und Rohrwand Reibungseffekte auftreten. Da das Fluid aufgrund der Haftbedingung aber ohnehin an der Wand haftet und die laminaren Schichten die Rauigkeiten der Wand überdecken, hat dies keinen zusätzlichen Einfluss auf den Druckverlust. Der gesamte Druckverlust bleibt also bei einer laminaren Strömung auf Gleichung (\ref{a}) beschränkt. Anders sieht dies bei turbulenten Strömungen aus, auf die im nächsten Abschnitt näher eingegangen wird.

Druckverlust bei turbulenter Rohrströmung

Turbulenzen in der Strömung bedeuten letztlich Verwirbelungen. Diese beinhalten zwar kinetische Energie beinhalten, aber diese Energie wird nicht wirklich transportiert. Stromabwärts kommt diese Energie sozusagen nicht an und ist deshalb im technisch nutzbaren Sinne verloren. Es existiert neben dem viskositätsbedingten Druckverlust durch Reibung somit ein zusätzlicher Druckverlust durch Turbulenz. Der Druckverlust ist bei turbulenter Strömung somit größer als bei laminarer Strömung.

Viskose Unterschicht

Bei turbulenten Strömungen hat die Rauigkeit der Rohrwand großen Einfluss auf den Rohrreibungskoeffizienten. Hierzu betrachten wir die Situation des Fluids an der rauen Rohrwand etwas genauer. Zunächst haften auch bei einer turbulenten Strömung die unmittelbar an der Wand befindlichen Fluidteilchen aufgrund der Haftbedingung dort an. Dabei können sich in unmittelbarer Umgebung zur Wand allerdings keine Turbulenzen ausbilden, da Querströmungen durch Wand verhindert werden (das Fluid kann ja schließlich nicht durch die Wand strömen). Deshalb bildet sich in unmittelbarer Umgebung zur Wand eine sogenannte laminare Unterschicht, die auch als viskose Unterschicht bezeichnet wird.

Je nachdem wie dick diese viskose Unterschicht ist und wie groß die Rauigkeiten sind, überdeckt die Unterschicht mehr oder weniger stark die Rauigkeiten der Wand. Sind die Rauigkeiten zu groß, dann beeinflussen diese sehr stark die Strömung und führen zu erhöhten Turbulenzen. Diese wiederum bewirken einen relativ großen Druckverlust. Sind die aus der viskosen Unterschicht herausragenden Oberflächenrauigkeiten hingegen relativ klein, dann ist die Turbulenz und damit der Druckverlust geringer. Werden die Oberflächenrauigkeiten hingegen vollständig von der viskosen Unterschicht überdeckt, dann ist der Druckverlust durch die Turbulenz in der Strömung am geringsten. Man spricht in diesem Fall auch von einem hydraulisch glatten Rohr.

Ein Rohr wird als hydraulisch glatt bezeichnet, wenn die viskose Unterschicht die Oberflächenrauigkeiten vollständig überdecken. Der Druckverlust ist dabei am geringsten!

Relative Rauheit

Die Rauigkeit einer Oberfläche wird durch die sogenannte gemittelte Rautiefe k angegeben (in der Technik auch mit R_z symbolisiert). Dieser Rauigkeitskennwert beschreibt den über mehrere Messstrecken gemittelte Abstand zwischen tiefster und höchster Stelle einer rauen Oberfläche.

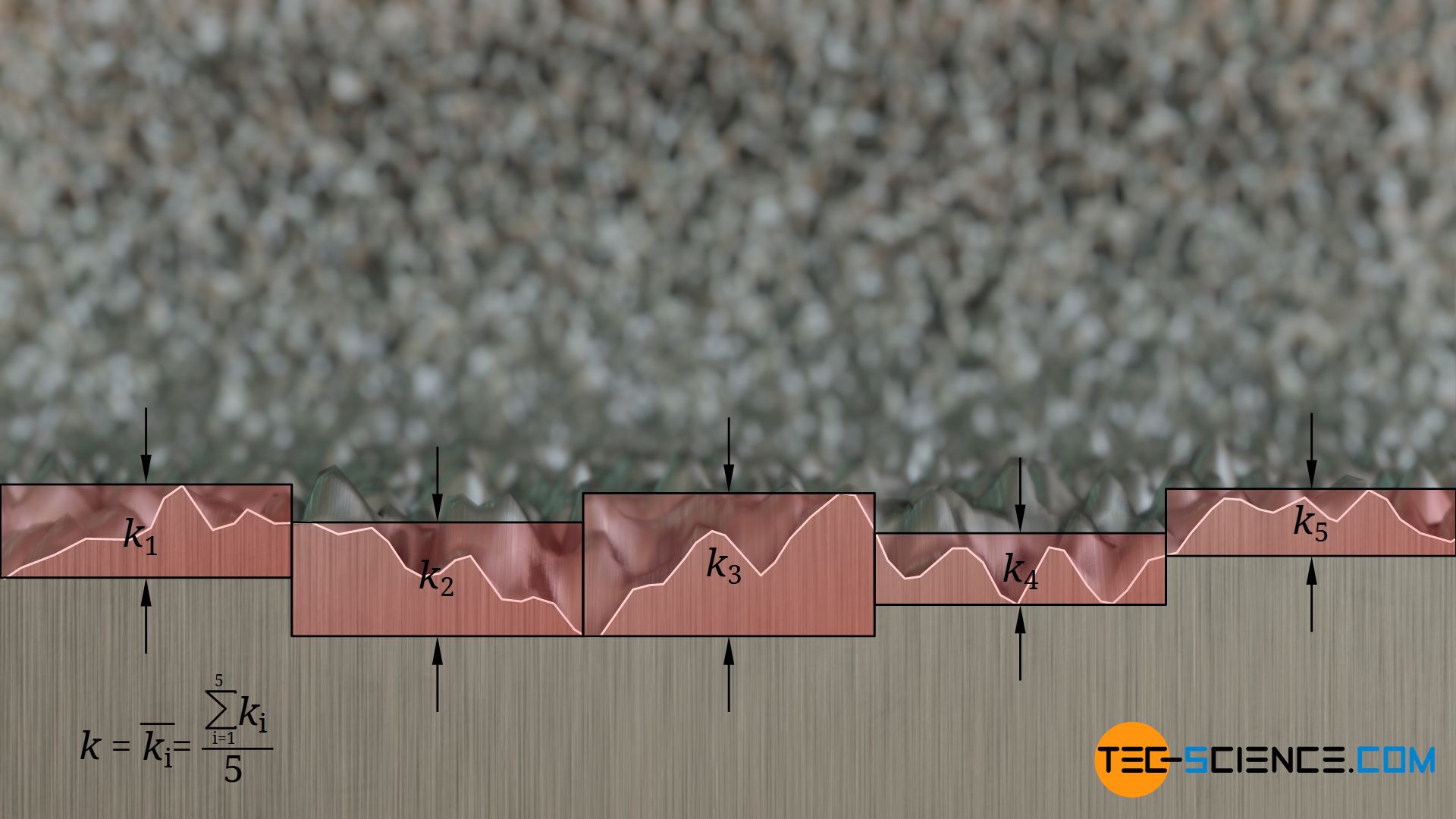
Die gemittelte Rautiefe als Absolutmaß für die Rauigkeit der Rohrwand ist zur Charakterisierung des Einflusses auf die turbulente Strömung aber nicht geeignet. Die Rauigkeit, die letztlich den Randbereich der Strömung beeinflusst, muss immer im Verhältnis zum gesamten Strömungsquerschnitt betrachtet werden, d.h. zum Innendurchmesser des Rohres. Das Verhältnis von absoluter Rauheit k und Rohrdurchmesser d wird auch als relative Rauheit ε bezeichnet:

\begin{align}
\label{e}
&\boxed{\varepsilon= \frac{k}{d}} ~~~\text{relative Rauheit}\\[5px]
\end{align}

Die relative Rauheit gibt anschaulich an, wie viel Prozent des gesamten Rohrdurchmessers die Rauigkeiten einnehmen.

Achtung: In der deutschsprachigen Literatur wird der Begriff der relativen Rauheit häufig auch umgekehrt definiert, d.h. als Verhältnis von Rohrdurchmesser zu Rautiefe:

\begin{align}
&\text{„relative Rauheit“}= \frac{d}{k} ~~~~~\text{(weit verbreitete Definition)}\\[5px]
\end{align}

Diese ist insofern sehr ungeschickt, weil diese Größe dann eigentlich genau das Gegenteil einer Rauheit beschreibt, nämlich die Glattheit: Umso größer der Quotient, desto weniger rau das Rohr! Aufgrund dieser missverständlichen Begrifflichkeit möchten wir deshalb bei der Definition der relativen Rauheit gemäß Gleichung (\ref{e}) bleiben!

Implizite Colebrook-White-Gleichung

Die Wissenschaftler Colebrook und White leiteten unter Einbeziehung empirischer Ergebnisse folgende implizite Gleichung zur Bestimmung der Rohrreibungszahl λ_tur für turbulente Rohrströmungen her:

\begin{align}
\label{cw}
&\boxed{\color{red}{\frac{1}{\sqrt{\lambda_\text{tur}}}}=-2\cdot \log_\text{10}\left(\frac{2,51}{Re} \cdot \color{red}{\frac{1}{\sqrt{\lambda_\text{tur}}}} +\frac{\varepsilon}{3,71}\right)} ~~~\text{Colebrook-White-Gleichung} \\[5px]
\end{align}

Der Begriff implizit bedeutet an dieser Stelle, dass diese Gleichung nicht direkt nach der Rohrreibungszahl aufgelöst werden kann. Vielmehr gilt es bei gegebener Reynoldszahl Re der Strömung und gegebener relativer Rauheit ε des Rohres, eine Rohrreibungszahl zu finden, die dann dieser Gleichung genügt. Ist dies der Fall, so entspricht die gefundene Rohrreibungszahl dem gesuchten Wert. Im Abschnitt Explizite Haaland-Gleichung wird auf ein iteratives Lösungsverfahren dieser Gleichung näher eingegangen. Im sogenannten Moody-Diagramm können die Rohrreibungszahlen auch graphisch ermittelt werden.

Für hydraulisch glatte Rohre überdeckt die viskose Unterschicht die Rauigkeiten der Wand. In diesem Fall ist die relative Rauheit ε in der Colebrook-White-Gleichung Null zu setzen ist, unabhängig des rechnerisch erhaltenen Wertes:

\begin{align}
&\boxed{\color{red}{\frac{1}{\sqrt{\lambda_\text{tur}}}}=-2\cdot \log_\text{10}\left(\frac{2,51}{Re} \cdot \color{red}{\frac{1}{\sqrt{\lambda_\text{tur}}}} \right)} ~~~\text{hydraulisch glatte Rohre} \\[5px]
\end{align}

Ragen die Unebenheiten der Rohrwand vollständig aus der viskosen Unterschicht heraus, dann ist die Rohrreibungszahl nahezu ausschließlich durch die Wandrauigkeiten bestimmt und unabhängig der Reynoldszahl. Der Wissenschaftler Nikuradse leitete für solche hydraulisch rauen Rohre folgende explizite Gleichung zur Bestimmung der Rohrreibungszahl her:

\begin{align}
&\boxed{\color{red}{\frac{1}{\sqrt{\lambda_\text{tur}}}}=-2\cdot \log_\text{10}\left(\frac{\varepsilon}{3,71} \right)} ~~~\text{hydraulisch raue Rohre} \\[5px]
&f_\text{tur}=\frac{1}{\left[2\cdot \log_\text{10}\left(\frac{3,71}{\varepsilon} \right)\right]^2} \\[5px]
\end{align}

Explizite Haaland-Gleichung

Es hat einen Grund, weshalb die Colebrook-White-Gleichung (\ref{cw}) in dieser zunächst etwas komisch anmutenden Form gegeben ist. Dies ermöglich nämlich ein iteratives Vorgehen, sodass die die gesuchte Rohrreibungszahl ausgehend eine Startwertes 1/√λ_tur,0 bestimmt werden kann. Der Startwert lässt sich dabei durch die von Haaland vorgeschlagene explizite Gleichung ermitteln:

\begin{align}
&\boxed{\color{red}{\frac{1}{\sqrt{\lambda_\text{tur,0}}}}=-1,8\cdot \log_\text{10}\left(\frac{6,9}{Re} +\left(\frac{\varepsilon}{3,7}\right)^{1,11}\right)} ~~~\text{Haaland-Gleichung} \\[5px]
\end{align}

Der mit der Haaland-Gleichung explizit ermittelte Wert 1/√λ_tur,0 kann nun in die rechte Seite der Colebrook-White-Gleichung eingesetzt werden. Hierdurch ergibt sich gemäß der linken Seite der Gleichung schließlich ein neuer Wert 1/√λ_tur,1. Dieser kann anschließend wieder in die rechte Seite der Gleichung eingesetzt werden. Der nach zwei Durchläufen erhaltene Wert 1/√λ_tur,2 entspricht in der Regel mit hinreichender Genauigkeit dem gesuchten Wert 1/√λ_tur. Damit lässt sich schließlich die Rohrreibungszahl λ_tur ermitteln.

Alternativ zur Haaland-Gleichung kann als Startwert auch ein Wert von 1/√λ_tur,0=7,5 genutzt werden. Dies entspricht dem Ergebnis der Haaland-Gleichug für ein hydraulisch glattes Rohr (ε=0) und einer Reynolds-Zahl von Re =10⁵.

Verlustleistung

Jeder Druckverlust in einer Rohrleitung muss durch die Leistung einer entsprechenden Pumpe kompensiert werden. Die Verlustleistung P_V aufgrund des Druckverlustes Δp_V ist abhängig vom Volumenstrom V*:

\begin{align}
\label{v}
&P_\text{V} = \Delta p_\text{V} \cdot \dot V \\[5px]
\end{align}

Wird der Druckverlust Δp_V nach Gleichung (\ref{volu}) eingesetzt, so folgt:

\begin{align}
\label{dr}
&\boxed{P_\text{V} = \lambda \cdot \frac{8\rho~L}{\pi^2} \cdot \frac{\dot{V}^3}{d^5}} ~~~\text{gilt allgemein}\\[5px]
\end{align}

An dieser Stelle gilt wieder zu beachten, dass die Rohrreibungszahl λ abhängig von der Reynolds-Zahl und damit von der Strömungsgeschwindigkeit ist. Die Strömungsgeschwindigkeit wiederum hängt vom Volumenstrom und vom vorhandenen Rohrdurchmesser ab!

Lediglich für laminare Strömungen gilt zwischen der Reynolds-Zahl und der Rohrreibungszahl ein expliziter Zusammenhang gemäß Formel (\ref{a}). In diesem Fall kann der Druckverlust für laminare Strömungen gemäß Gleichung (\ref{lam2}) direkt in Formel für die Verlustleistung (\ref{v}) eingesetzt werden. Für den Fall von laminaren Rohrströmungen gilt dann folgender Zusammenhang:

\begin{align}
&P_\text{V,lam} = \Delta p_\text{V,lam} \cdot \dot V \\[5px]
&\boxed{P_\text{V,lam} = \frac{128~\eta ~ L}{\pi} \cdot \frac{\dot{V}^2}{d^4}} ~~~\text{gilt nur für laminare Strömungen}\\[5px]
\end{align}

Druckverlust durch einzelne Bauteile (Druckverlustbeiwert)

Ein Rohrsystem enthält in der Regel nicht nur ein einziges gerades Rohr. Meist besteht ein Rohrsystem aus mehreren Rohrbögen (Krümmer), Verzweigungen, Reduzierungen, Erweiterungen, Ventile, etc. Diese einzelnen Bauteile haben ebenfalls Energieverluste und damit Druckverluste zur Folge.

Beschrieben werden diese Druckverluste durch jeweils einen Druckverlustbeiwert ζ (auch Widerstandsbeiwert genannt). Der Druckverlustbeiwert ist analog zur Rohrreibungszahl definiert, d.h. als Verhältnis zwischen Druckverlust Δp_V im Bauteil und dem dynamischen Druck der Strömung p_dyn:

\begin{align}
& \zeta:= \frac{\Delta p_\text{V}}{p_\text{dyn}} ~~~\text{mit}~~~ p_\text{dyn}=\tfrac{1}{2}\rho ~\bar v^2 ~~~\text{folgt:} \\[5px]
\label{zeta}
& \boxed{\zeta= \frac{\Delta p_\text{V}}{\tfrac{1}{2}\rho ~\bar v^2} } ~~~\text{Druckverlustbeiwert} \\[5px]
\end{align}

Die Bedeutung des Druckverlustbeiwerts bei durchströmten Körpern ist letztlich identisch mit dem Widerstandsbeiwert bei umströmten Körpern.

Der Druckverlustbeiwert ist eine dimensionslose Ähnlichkeitskenngröße zur Beschreibung des Druckverlust in einzelnen Bauteilen (Krümmer, Ventile, Reduzierstücke, Erweiterungen, etc.)!

Die Druckverlustbeiwerte für die verschiedenen Bauteile werden in der Regel auf experimentellem Wege ermittelt und sind in Tabellenbüchern angegeben. Bei bekanntem Druckverlustbeiwert lässt sich der Druckverlust durch das Bauteil dann wie folgt ermitteln:

\begin{align}
\label{dez}
& \boxed{\Delta p_\text{V} = \zeta \cdot \frac{1}{2}\rho ~\bar v^2 } ~~~\text{Druckverlust in einzelnen Bauteilen} \\[5px]
\end{align}

Die Strömungsgeschwindigkeit bezieht sich grundsätzlich auf die Geschwindigkeit des Fluids vor dem eigentlichen Bauteil und nicht auf die Strömungsgeschwindigkeit im Bauteil! Ein Ventil bspw. reduziert je nach Stellung den strömenden Querschnitt und erhöht im Bauteil somit die Strömungsgeschwindigkeit. Die für die Druckverlustberechnung zugrunde zulegende Strömungsgeschwindigkeit bezieht sich aber auf die Strömungsgeschwindigkeit in der Zuleitung!

Letztlich kann man auch für einen geraden Rohrabschnitt einen Druckverlustbeiwert definieren. Auf diese Weise können auch die geraden Rohrabschnitte als Einzelwiderstände betrachtet werden. In diesem Fall steht der Druckverlustbeiwert über die Länge des Rohrabschnitts L und dem Rohrinnendurchmesser d wie folgt mit der Rohrreibungszahl λ in Zusammenhang:

\begin{align}
&\boxed{\zeta_\text{R} = \frac{L}{d} \lambda}~~~\text{Druckverlustbeiwert eines geraden Rohrabschnitts} \\[5px]
\end{align}

Umgekehrt lässt sich für Einzelwiderstände eine äquivalente Rohrlänge L_ä angeben. Man kann sich die einzelnen Bauteile somit als zusätzliche Rohrabschnitte gedacht vorstellen. In der unten angegebenen Gleichung, entspricht λ dabei der Rohrreibungszahl der eigentlichen Rohre.

\begin{align}
&\boxed{L_\text{ä}= \frac{d \cdot \zeta}{\lambda}}~~~\text{äquivalente Rohrlänge von Bauteilen} \\[5px]
\end{align}

Bei einem Rohrdurchmesser von d = 1 cm und einem Druckverlustbeiwerte von ζ=1 sowie einer Rohrreibungszahl von λ = 0,02 erhält man eine äquivalente Rohrlänge von nur 0,5 m. Bei sehr langen Rohrleitungssystemen und wenigen Einzelwiderständen (was häufig der Fall ist) kann der Druckverlust durch die eingebauten Komponenten also meist vernachlässigt werden.

Im Allgemeinen gilt aber: Die Summe der Druckverluste Δp_V,R durch die einzelnen geraden Rohrabschnitte, plus die Summe der Druckverluste Δp_V,E durch die Einzelwiderstände, ergibt schließlich den Gesamtdruckverlust Δp_V,ges des gesamten Rohrleitungssystems:

\begin{align}
&\boxed{\Delta p_\text{V,ges} = \sum \Delta p_\text{V,R} +\sum \Delta p_\text{V,E} } \\[5px]
\end{align}

Bei nur einer Rohrleitung der Länge L mit konstantem Innendurchmesser d und damit konstanter mittlerer Strömungsgeschwindigkeit v gilt:

\begin{align}
&\boxed{\Delta p_\text{V,ges} = \left(\lambda \frac{L}{d} + \sum \zeta \right) \frac{1}{2}\rho~\bar{v}^2} \\[5px]
\end{align}