Der Wärmeübergangskoeffizient beschreibt den konvektiven Wärmeübergang von einem Festkörper auf ein strömendes Fluid und umgekehrt!
Einleitung
Der Wärmeübergangskoeffizient beschreibt den konvektiven Wärmeübergang von einem Festkörper auf ein strömendes Fluid (Gas bzw. Flüssigkeit) oder umgekehrt. Eine solche Situation zeigt sich bspw. an einem Heizkörper. Kalte Luft strömt durch die Thermik am Heizkörper vorbei (freie Konvektion) und wird erwärmt. Offensichtlich überträgt der Heizkörper Wärme auf die vorbeiströmende Luft.

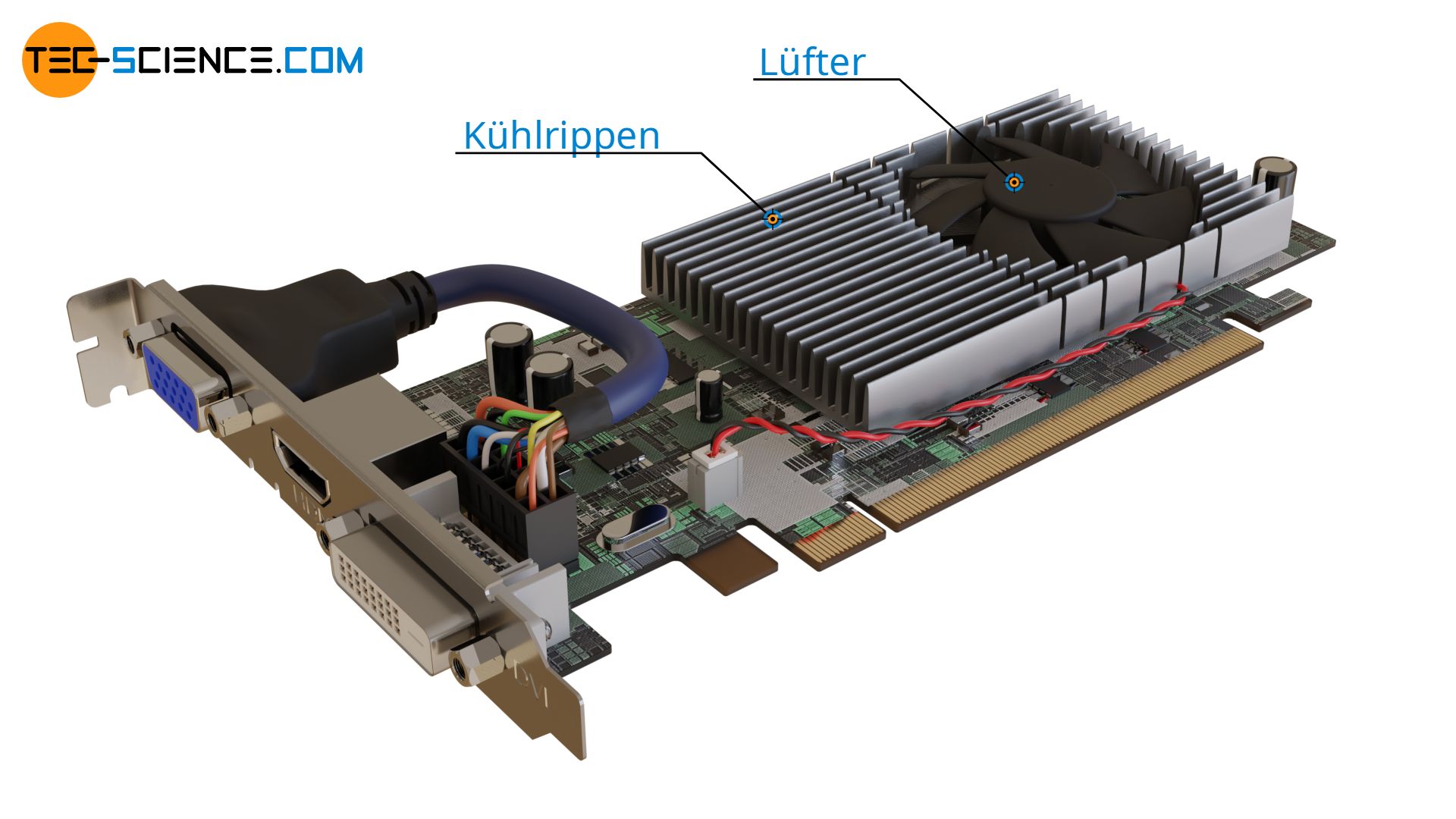
Auch bei der Kühlung von Grafikkarten zeigt sich ein solcher konvektiver Wärmeübergang von den erwärmten Kühlrippen auf einen Luftstrom, der von einem Lüfter erzeugt wird. Im Fall einer Wasserkühlung, würde die Wärme nicht mehr an strömendes Gas abgegeben, sondern auf strömende Flüssigkeit. In beiden Fällen handelt es allerdings nicht mehr um eine freie Konvektion, sondern um eine erzwungen Konvektion durch den Lüfter bzw. durch die Pumpe.
Definition des Wärmeübergangskoeffizienten
Die Temperaturdifferenz zwischen Festkörper und Fluid stellt wie immer bei thermodynamischen Vorgängen den Antrieb für den Wärmefluss dar. Der vom Feststoff auf das Fluid übertragene Wärmestrom Q* ist umso größer, je größer die Temperaturdifferenz zwischen der festen „Wand“ TW und dem strömenden Fluid TF ist. Der Wärmestrom ist dabei proportional zur Temperaturdifferenz:
\begin{align}
&\dot Q \sim (T_W-T_F) \\[5px]
\end{align}
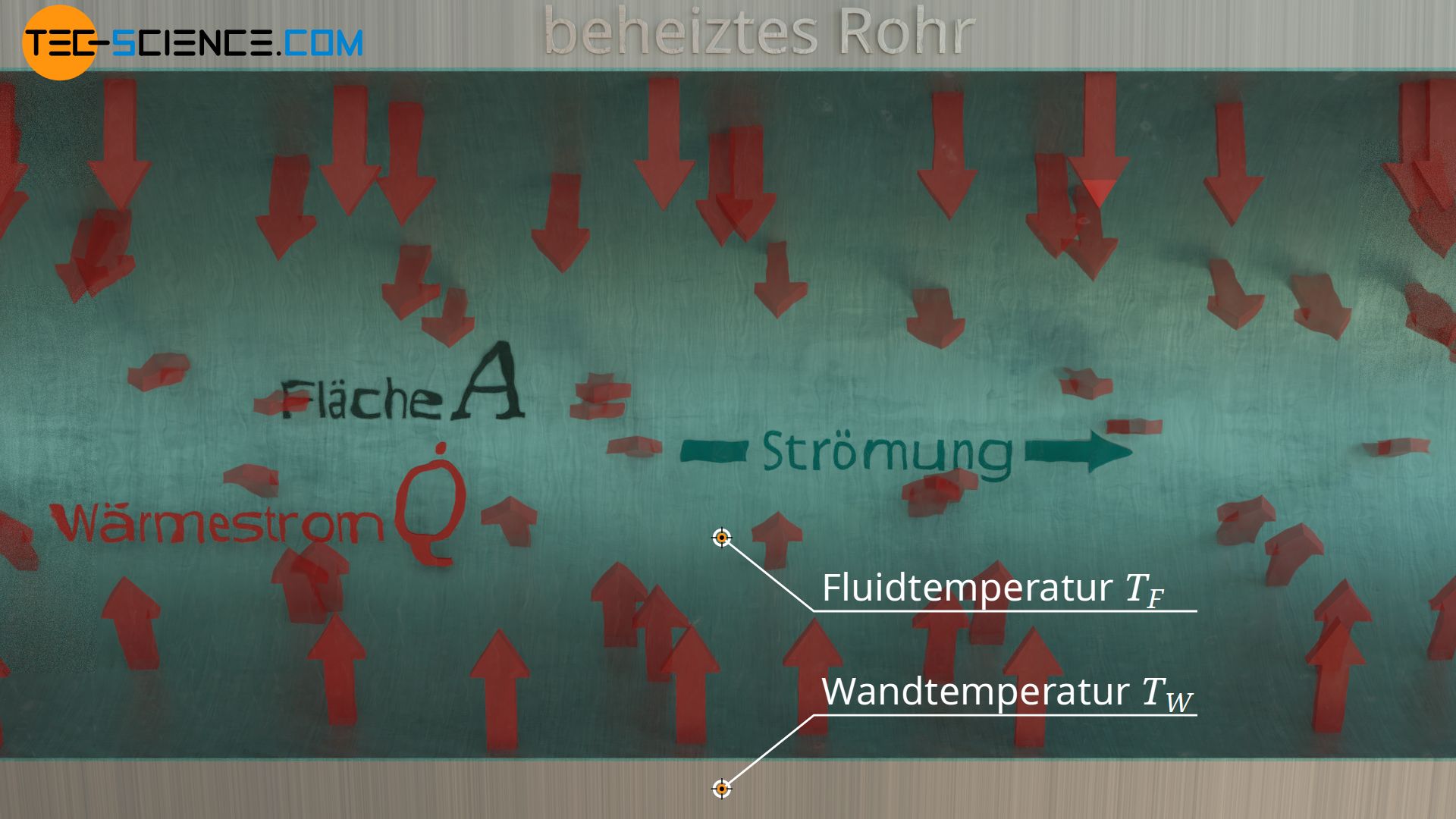
Zudem hängt hängt der Wärmestrom von der Fläche ab, mit der der Feststoff in Kontakt mit dem vorbeiströmenden Fluid steht. Diese Fläche kann die gesamte Innenfläche des Rohres umfassen, wenn bspw. das gesamte Rohr erwärmt wird, oder aber nur ein Teil des Rohres, wenn das Rohr nur punktuell erwärmt wird. Umso größer die Fläche, desto mehr Wärme kann übertragen werden, und umso größer ist der Wärmestrom durch diese Fläche. Aus diesem Grund bestehen Kühlkörper von Chips aus vielen Kühlrippen, um damit eine möglichst große Fläche zu erzeugen. Auch Heizkörper nutzen dieses Prinzip durch die Verwendung vieler einzelner Heizrippen. Dabei besteht ein proportionaler Zusammenhang zwischen Fläche A und Wärmestrom Q*:
\begin{align}
&\dot Q \sim A \\[5px]
\end{align}
Der Wärmestrom ist also insgesamt proportional zur Temperaturdifferenz und zur Fläche, sodass durch Einführung eines Proportionalitätsfaktors α der Wärmestrom beim Wärmeübergang zwischen Festkörper und Fluid wie folgt ermittelt werden kann:
\begin{align}
&\dot Q \sim A \cdot (T_W-T_F) \\[5px]
\label{q}
&\boxed{\dot Q = \alpha \cdot A \cdot (T_W-T_F)} \\[5px]
\label{qq}
&\boxed{\dot q = \alpha \cdot (T_W-T_F)} ~~~\boxed{\dot q = \frac{\dot Q}{A}} ~~~\text{Wärmestromdichte} \\[5px]
\end{align}
In Gleichung (\ref{qq}) wurde der Quotient aus Wärmestrom und Fläche zur sogenannten Wärmestromdichte zusammengefasst. Die Wärmestromdichte beschreibt letztlich den Wärmestrom pro Flächeneinheit. Mit Fläche ist dabei die Fläche an der Wand gemeint. Der Proportionalitätsfaktor α kann in diesem Zusammenhang somit ganz allgemein als Verhältnis zwischen Wärmestromdichte und Temperaturdifferenz definiert werden und wird Wärmeübergangskoeffizient genannt:
\begin{align}
\label{a}
&\boxed{\alpha := \frac{\dot q}{T_W-T_F}} ~~~\text{Wärmeübergangskoeffizient}\\[5px]
\end{align}
Der Wärmeübergangskoeffizient beschreibt den konvektiven Wärmeübergang von einem Festkörper auf ein strömendes Fluid und umgekehrt!
Achtung: Grundsätzlich darf der Wärmeübergangskoeffizienten nicht mit dem Wärmeleitkoeffizienten verwechselt werden. Der Wärmeleitkoeffizient beschreibt die Wärmeleitung im Inneren eines Stoffes, während der Wärmeübergangskoeffizienten den Wärmeübergang zwischen zwei unterschiedlichen Stoffen aufgrund von Konvektionsvorgängen beschreibt.
Einflussgrößen auf den Wärmeübergangskoeffizienten
Die Gleichungen (\ref{q}) bzw. (\ref{qq}) gelten grundsätzlich auch für den umgekehrten Fall, wenn bspw. Wärme von einem strömenden Fluid auf einen Festkörper übertragen wird. Eine solche Situation findet man zum Beispiel im Inneren des Heizkörpers wieder, wenn das strömende Wasser Wärme auf den Heizkörper überträgt. Dabei herrscht im Fluid jedoch eine andere Temperaturverteilung. Dies wiederum beeinflusst den Wärmeübergangskoeffizienten, trotz evtl. identischen Temperaturdifferenzen. Der Wärmeübergangskoeffizient ist also auch abhängig von der Wärmestromrichtung.
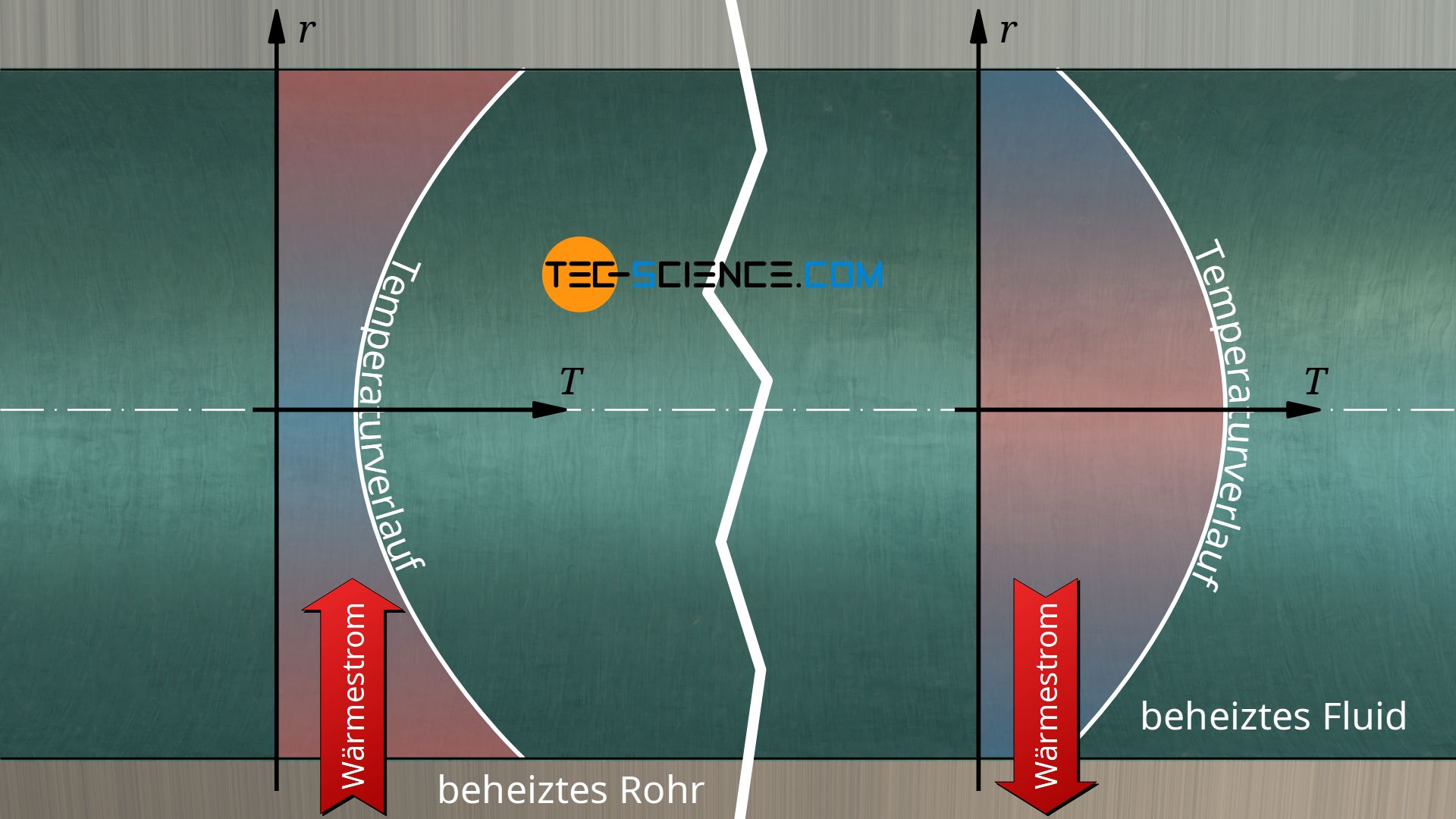
Im Gegensatz zum Wärmeleitkoeffizienten, handelt es sich beim Wärmeübergangskoeffizienten nicht um eine Stoffkonstante. Der Wärmeübergangskoeffizient hängt unter anderem von der Stoffpaarung ab, d.h. von der Paarung Festkörper/Fluid. Auch die Oberflächenbeschaffenheit (Rauigkeit) des Festkörpers spielt eine Rolle. Zudem beeinflusst die Strömungsgeschwindigkeit den Wärmeübergang. Dabei spielt insbesondere die Art der Strömung eine Rolle, d.h. ob die Strömung laminar order turbulent ist.
Der Wärmeübergangskoeffizient zwischen Feststoff und strömendem Fluid wird unter anderem beeinflusst durch Stoffpaarung, Oberflächenbeschaffenheit, Strömungsgeschwindigkeit und Strömungsart und Wärmestromrichtung!
Des Weiteren hängt der Wärmeübergangskoeffizient von der Größe des Systems ab. Im Fall eines Rohres also vom Durchmesser bzw. im Falle einer Platte von der Plattengröße. Für ähnliche Strömungsbedingungen, erhält man für größere Systeme geringere Wärmeübergangskoeffizienten. Der Wärmeübergangskoeffizient ist also immer abhängig vom konkreten Anwendungsfall. Eine allgemeine Beschreibung von Konvektionsprozessen ist daher ohne weiteres nicht möglich. Eine solche allgemeine Beschreibung wird erst durch Einführung einer dimensionslosen Ähnlichkeitskenngröße möglich, der sogenannten Nusselt-Zahl. Mehr Informationen hierzu finden Sie im verlinkten Artikel.
Bezugstemperaturen
Wenn, wie im Falle des Heizkörpers von der Temperatur der vorbeiströmenden Luft die Rede ist, stellt sich natürlich die Frage, worauf sich diese Temperatur genau bezieht. In der Nähe des Heizkörpers ist nämlich die Lufttemperatur offensichtlich höher als in größerem Abstand davon. Meist bezieht sich der Wärmeübergangskoeffizient deshalb auf die Fluidtemperatur in einem hinreichend großen Abstand zur Wand, wo sich die Temperatur senkrecht zur Hauptströmungsrichtung* kaum noch ändert (deshalb wird anstelle von TF auch häufig das Symbol T∞ genutzt). Im Fall der Heizung entspräche dies salopp formuliert der Temperatur in Mitten des Raumes („Raumtemperatur“).

Auch bei einer Rohrströmung, wenn zum Beispiel das heiße Wasser durch das Rohrsystem des Heizkörpers strömt, herrschen im Fluid unterschiedliche Temperaturen. In der in der Mitte des Rohres (in der sog. Kernströmung), ist das Wasser heißer als in der Nähe der Rohrwand, wo das Fluid bereits Wärme auf das umgebende Rohr übertragen hat. Anders als im Falle der umgebenden Luft außerhalb des Heizkörpers, befindet sich das Wasser im Heizkörper jedoch nur in einem örtlich stark begrenzten Bereich. Man gibt bei einer Rohrströmung als Fluidtemperatur deshalb meist die mittlere Temperatur im Rohr an. Diese mittlere Temperatur entspräche der Mischungstemperatur, wenn man das Fluid ideal mischen würde.
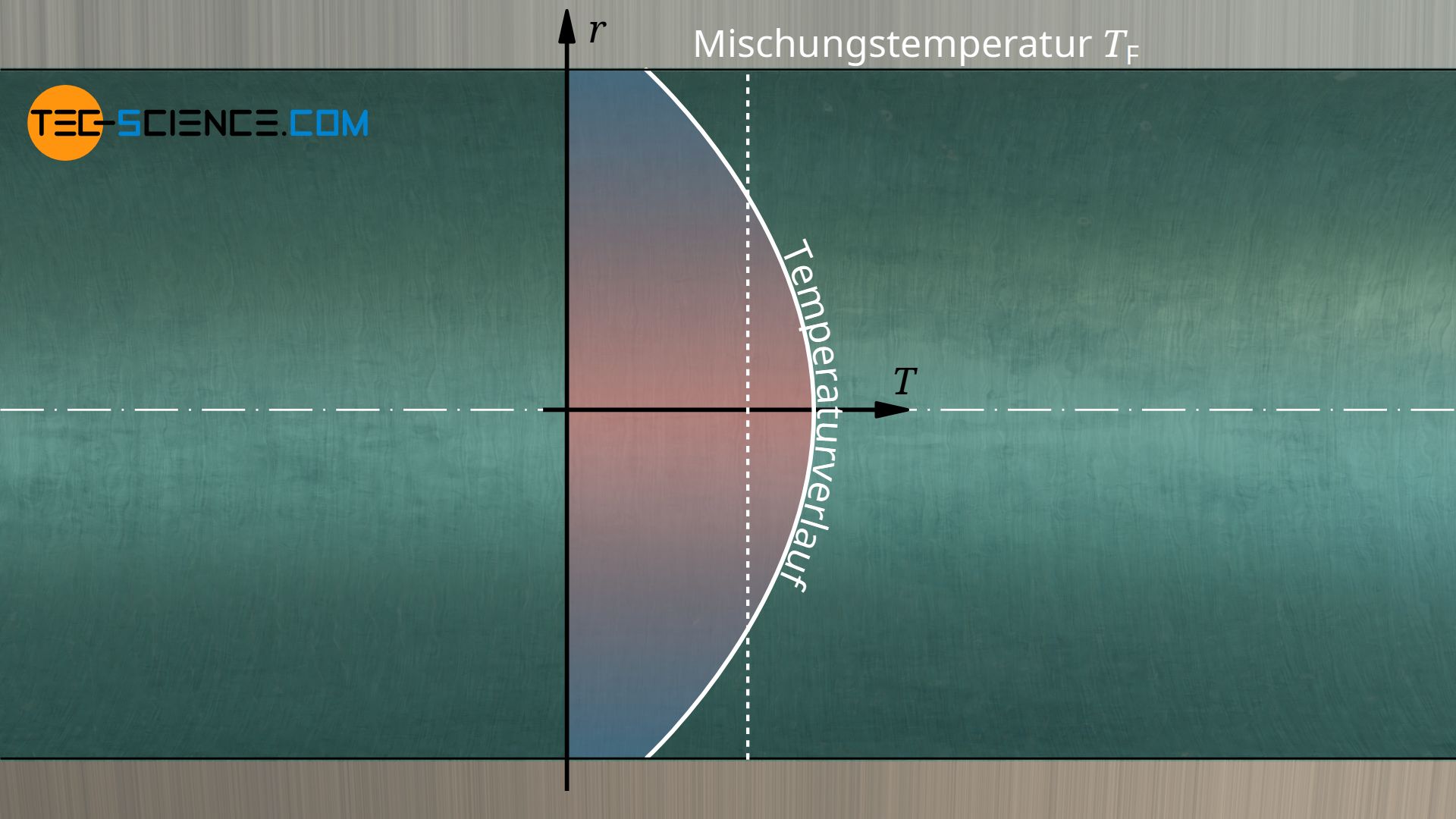
Die Fluidtemperatur bezieht sich bei örtlich nicht begrenzter Strömung (Außenströmung) auf die Temperatur in einem hinreichend großen Abstand zur Wand und bei Rohrströmung (Innenströmung) meist auf die mittlere Temperatur des Fluids!
*) Anmerkung: Neben der Hauptströmungsrichtung des Fluids, die in Rohrströmungen meist durch Pumpen erzwungen wird (erzwungene Konvektion), existiert aufgrund von Dichteunterschieden infolge von Temperaturunterschieden auch eine freie Konvektion. In der Praxis überlagern sich folglich beide Strömungen. Je nach Situation kann die freie Konvektion einen beachtlichen Anteil am gesamten Wärmeübergang haben.
Bedeutung der Grenzschicht für den Wärmeübergang
Strömt ein Fluid entlang einer Wand, so hat dies Auswirkungen auf die Strömungsgeschwindigkeit. Aufgrund der Reibungskräfte (beschrieben durch die Viskosität) zwischen Wand und Fluid sowie innerhalb des Fluids, wird die freie Strömung des Fluids gestört. Diese gestörte Schicht wird auch als Geschwindigkeitsgrenzschicht bezeichnet (auch hydrodynamische Grenzschicht genannt). Aufgrund der Haftbedingung ist die Geschwindigkeit des Fluids unmittelbar an der Wand null und steigt dann langsam an.
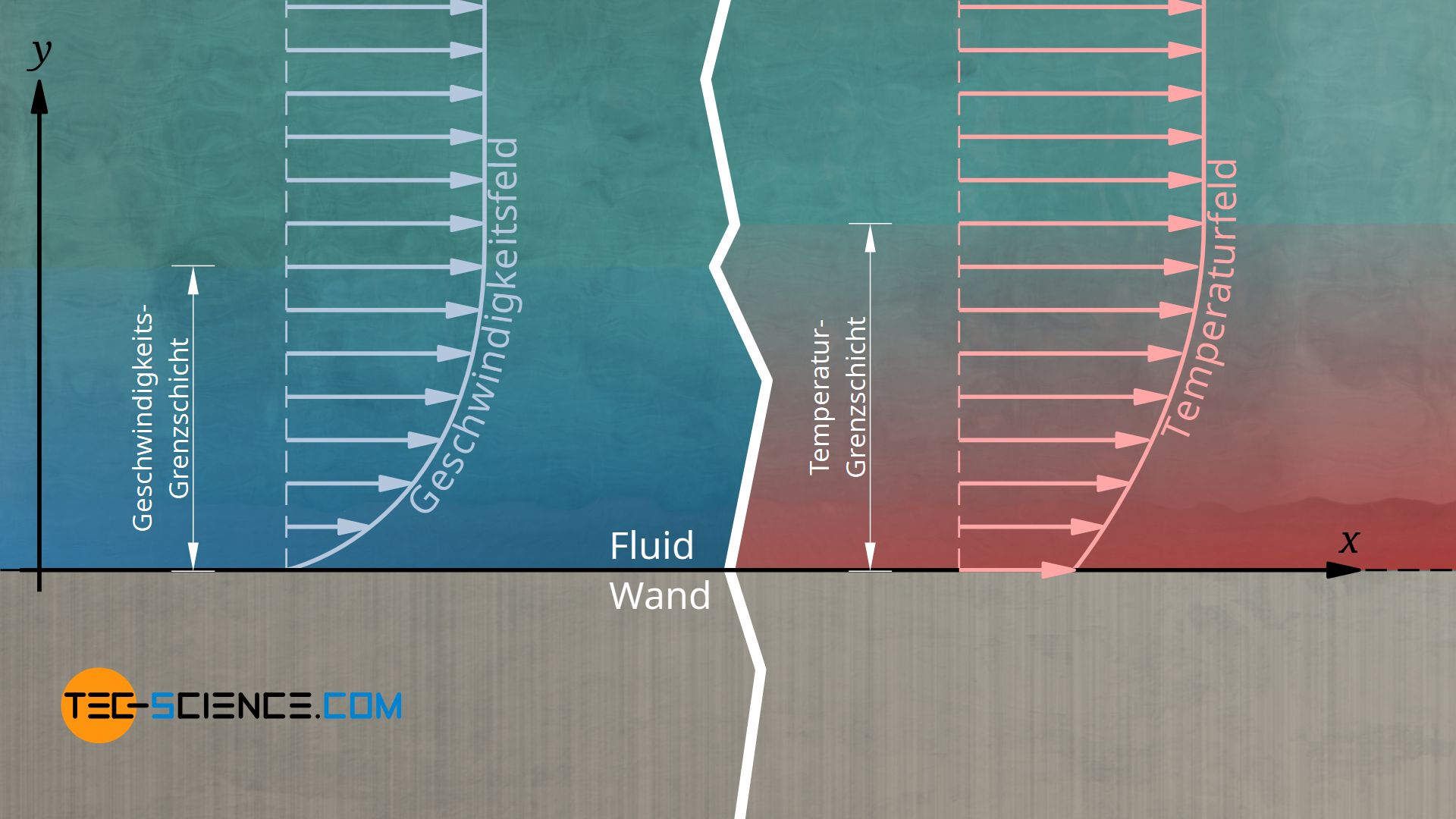
Da das Fluid also direkt an der Wand haftet und somit nicht der Konvektion unterliegt, ist dort ein Wärmetransport nur durch Wärmeleitung möglich. Beachte, dass dies aber bedeutet nicht, dass die Konvektion nicht den gesamten Wärmeübergang maßgeblich beeinflusst! Denn aufgrund der konvektiven Vorgänge ändert sich im Vergleich zu einer Situation ohne Konvektion das gesamte Temperaturfeld (das Verhältnis des Wärmetransports bei Vorhandensein von Konvektion im Vergleich zu einer Situation ohne Konvektion wird durch die sogenannte Nusselt-Zahl beschrieben)! Nichts desto trotz, gilt unmittelbar an der Wand somit das Fourier’sche Gesetz der Wärmeleitung (mit λF als Wärmeleitfähigkeit des Fluids):
\begin{align}
& \dot{q_W} =- \lambda_F \cdot \left(\frac{\text{d}T_F}{\text{d}y}\right)_\text{Wand} \\[5px]
\end{align}
Für den Wärmeübergangskoeffizienten folgt gemäß Gleichung (\ref{a}) deshalb:
\begin{align}
&\alpha = \frac{\dot q_W}{T_W-T_F}\\[5px]
\label{wand}
&\boxed{\alpha = \frac{- \lambda_F \cdot \left(\frac{\text{d}T_F}{\text{d}y}\right)_\text{Wand}}{T_W-T_F}}\\[5px]
\end{align}
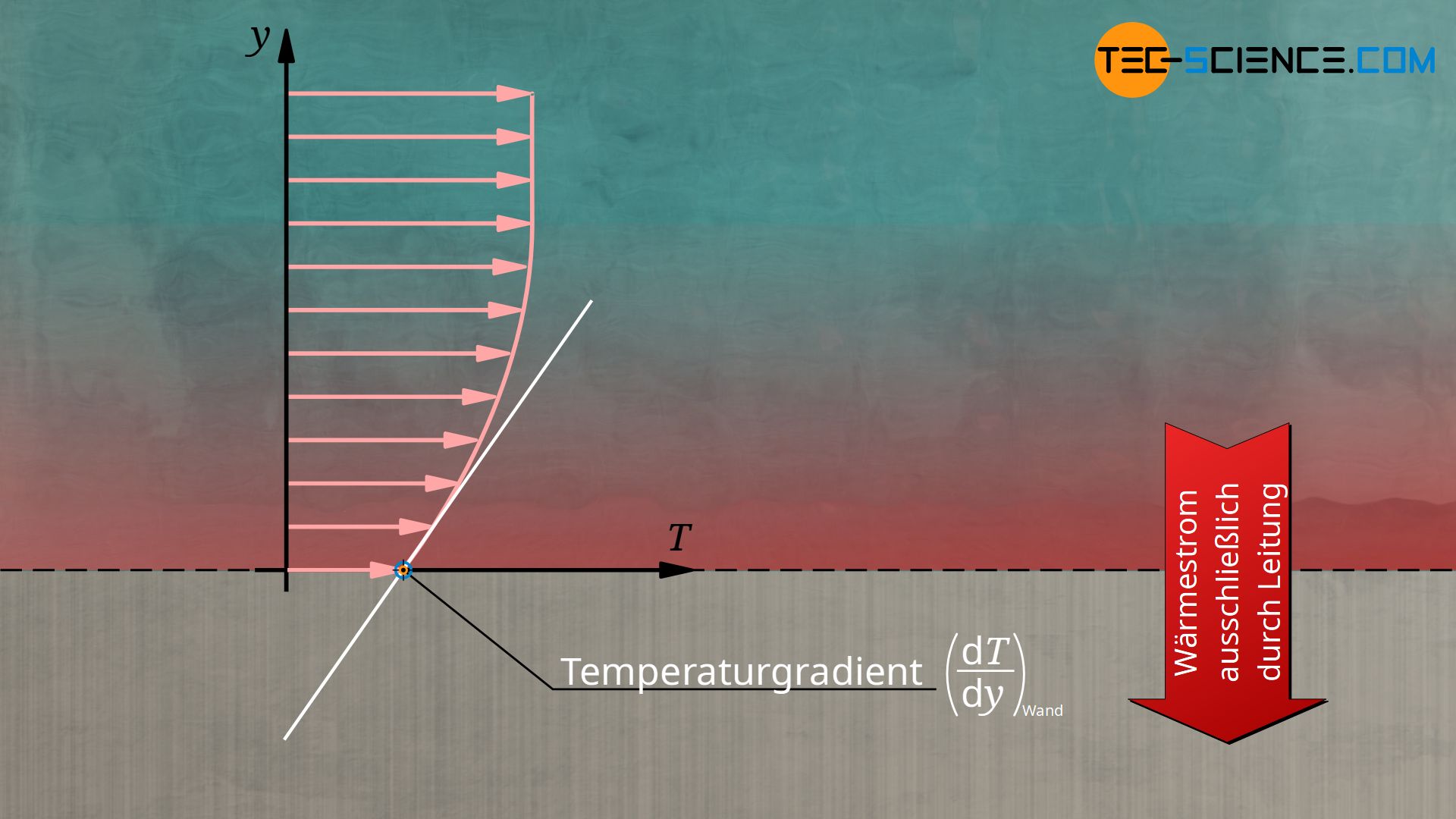
Wie man anhand dieser Gleichung erkennen kann, beeinflusst also der Temperaturgradient an der Wand maßgebend den Wärmeübergangskoeffizient. Die Verteilung der Temperatur im Fluid (Temperaturfeld) hängt aber von den Strömungsverhältnissen im Fluid ab (Geschwindigkeitsfeld). Umgekehrt beeinflusst das Temperaturfeld wiederum die Viskosität des Fluids und somit das Geschwindigkeitsfeld. Geschwindigkeitsfeld und Temperaturfeld beeinflussen sich also wechselseitig.
Die Grenzschicht zwischen Fluid und Wand hat entscheidenden Einfluss auf den gesamten konvektiven Wärmeübergang!
Lokaler und mittlerer Wärmeübergangskoeffizient
Die im Abschnitt zuvor erläuterte Grenzschicht ist im Allgemeinen kein einheitlicher Bereich, sodass sich je nach Ort unterschiedliche Strömungsbedingungen ergeben. Dies beeinflusst somit auch die Temperaturverläufe, insbesondere Temperaturgradienten an der Wand. Gemäß oberer Gleichung (\ref{wand}) führt dies somit je nach Ort zu anderen Wärmeübergangskoeffizienten. Man spricht in diesem Zusammenhang auch von einem lokalen Wärmeübergangskoeffizienten.
Um diese Situation besser zu verdeutlichen, betrachten wir eine isotherm beheizte Platte, die längs von einem Fluid angeströmt wird. Die Strömung selbst sei eben und laminar. Beim Aufströmen auf die Platte haftet die unmittelbar an der Wand befindliche Fluidschicht daran (Haftbedingung). Dies führt dazu, dass im weiteren Verlauf die darüber befindlichen Fluidschichten abgebremst werden. Der gestörte Bereich wächst somit allmählich an, bis sich irgendwann eine konstante Grenzschichtdicke δh ausgebildet hat.

Auf die analoge Weise bildet auch eine Temperaturgrenzschicht beim Überströmen des Fluids aus. Während die Temperatur innerhalb der ungestörten Anströmung in jedem Punkt konstant ist, erfolgt beim Überströmen über die Platte eine Erwärmung des Fluids. Im weiteren Verlauf dringt die Wärme tiefer in das Fluid ein. Es bildet sich über der Platte also nicht nur ein Bereich innerhalb dessen die Geschwindigkeit gestört ist, sondern auch ein Bereich innerhalb dessen die Temperatur gestört ist. Beide Grenzschichten unterscheiden sich im Allgemeinen voneinander (wie diese Grenzschichten genau definiert sind, erfahren Sie im Artikel Grenzschicht und dimensionslose Kenngrößen).
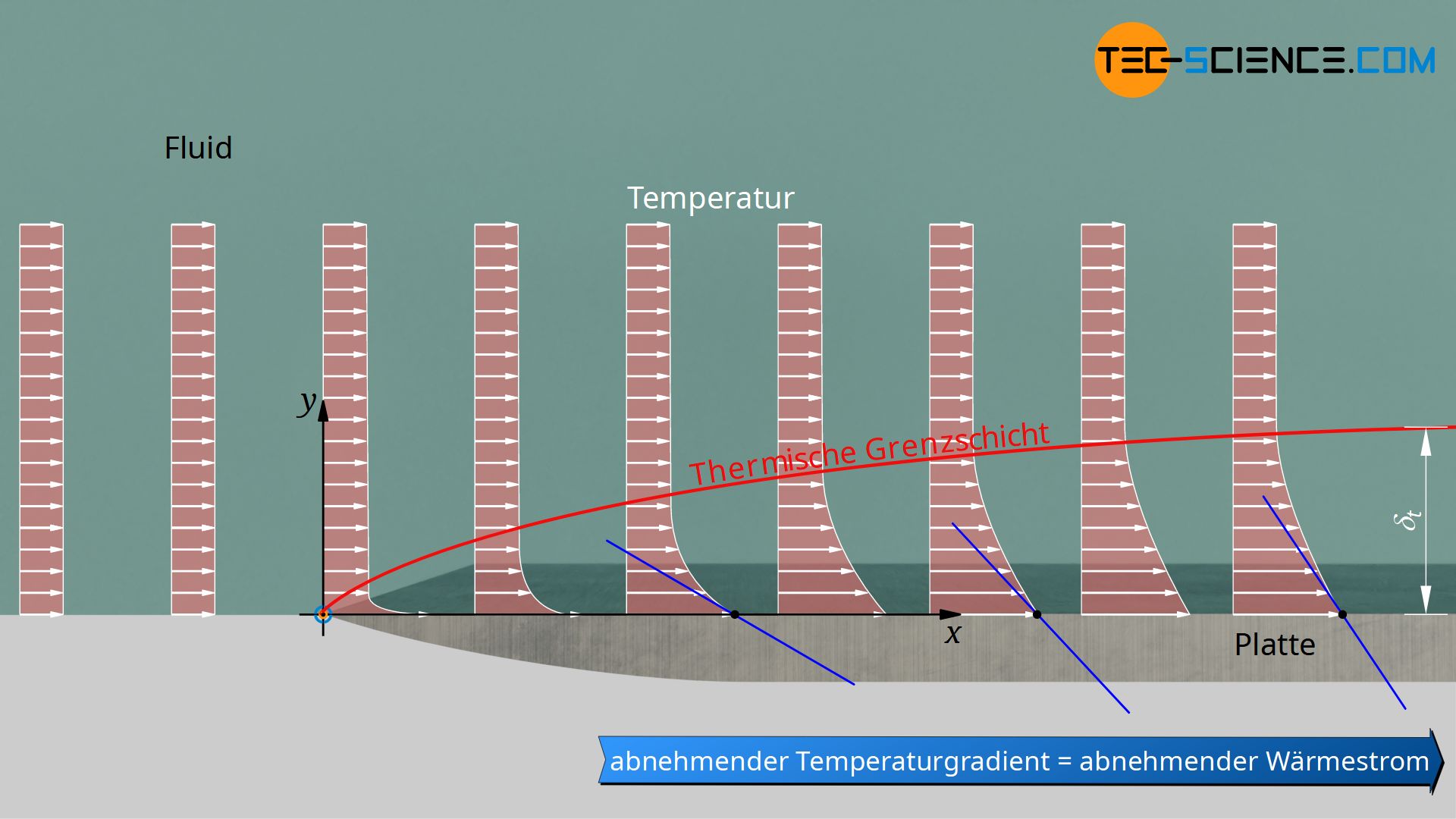
Es wird nun also deutlich, dass sich das wechselseitig beeinflussende Geschwindigkeitsfeld und Temperaturfeld von Ort zu Ort unterscheidet. Der Wärmeübergang unterscheidet sich somit ebenfalls von Ort zu Ort. Dementsprechend lässt sich an jeder Position x ein lokaler Wärmeübergangskoeffizient αlok definieren, mit dem die lokale Wärmestromdichte q*lok beschrieben wird:
\begin{align}
&\boxed{\dot q_\text{lok} = \alpha_\text{lok} \cdot (T_W-T_F)} ~~~~~\text{lokaler Wärmeübergang} \\[5px]
\end{align}
Beachte, dass sich die Temperatur TW auf die konstante Wandtemperatur und TF auf die Temperatur der ungestörten Anströmung bezieht. Der Ausdruck TW-TF ist also unabhängig der Position x stets konstant. Die lokale Wärmestromdichte wird also nur durch den lokalen Wärmeübergangskoeffizienten beeinflusst!
Mit Hilfe von Computersimulationen lassen sich relativ einfach die lokalen Wärmeübergangskoeffizienten ermitteln, sodass nach Integration der lokalen Wärmestromdichten über die gesamte Plattenfläche hinweg, der gesamte konvektive Wärmestrom Q* bestimmt werden kann:
\begin{align}
\label{dqq}
& \dot Q = \int \limits_A \dot q_\text{lok} ~ \text{d}A= (T_W-T_F) \int \limits_A \alpha_\text{lok} ~ \text{d}A \\[5px]
\end{align}
Mit der Definition eines mittleren Wärmeübergangskoeffizienten,
\begin{align}
\label{ma}
& \boxed{\overline{\alpha} =\frac{1}{A} \int \limits_A \alpha_\text{lok} ~ \text{d}A} ~~~~~\text{mittlerer Wärmeübergangskoeffizient} \\[5px]
\end{align}
kann dann schließlich der gesamte Wärmeübergang der Platte wie folgt ermittelt werden:
\begin{align}
\label{dq}
& \boxed{\dot Q = \overline{\alpha} \cdot A \cdot (T_W-T_F)} ~~~~~\text{gesamter konvektiver Wärmeübergang} \\[5px]
\end{align}
Beachte, dass Gleichung (\ref{ma}) in Gleichung (\ref{dq}) eingesetzt, letztlich Gleichung (\ref{dqq}) ergibt.
In diesem Zusammenhang soll nochmals Gleichung (\ref{wand}) näher betrachtet werden, die den (lokalen) Wärmeübergangskoeffizienten in Abhängigkeit des Temperaturgradienten an einer Stelle x an der Wand wiedergibt:
\begin{align}
&\boxed{\alpha_\text{lok} = \frac{- \lambda_F \cdot \left(\frac{\text{d}T_F}{\text{d}y}\right)_\text{Wand,x}}{T_W-T_F}}\\[5px]
\end{align}
Wird von einer konstanten Wärmeleitfähigkeit λF des Fluids ausgegangen, dann ist die einzige Größe die sich in dieser Gleichung über die Platte ändert, der Temperaturgradient. Mit fortschreitender Position x nimmt die Dicke der thermischen Grenzschicht zu, d.h. die Temperatur steigt über eine größere Distanz y an. Der Temperaturgradient nimmt in x-Richtung also ab und so auch der lokale Wärmeübergangskoeffizient. Die lokale Wärmestromdichte nimmt somit ebenfalls entlang der Platte ab (siehe Abbildung oben)!
Dies wird auch anschaulich klar, denn wenn man sich eine (unendlich) lange Platte vorstellt, dann wird sich das Fluid irgendwann so stark erwärmt haben, dass es (nahezu) dieselbe Temperatur wie das Rohr aufweist. In diesem Fall ist kein Temperaturgradient zwischen Wand und Fluid vorhanden und somit auch kein Antrieb für einen Wärmestrom. Der Wärmestrom muss also zwangsläufig beim Überströmen des Fluids über die isotherm beheizte Platte abnehmen, das sich die Temperaturen mehr und mehr angleichen.






