Planck’sches Strahlungsgesetz und Wien’sches Verschiebungsgesetz

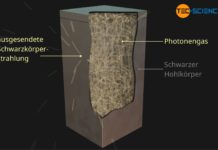
Das Planck’sche Strahlungsgesetz beschreibt die ausgesendete Strahlung von schwarzen Körpern und das Wien’sche Verschiebungsgesetz das spektrale Intensitätsmaximum dieser Strahlung.

Planck’sches Strahlungsgesetz

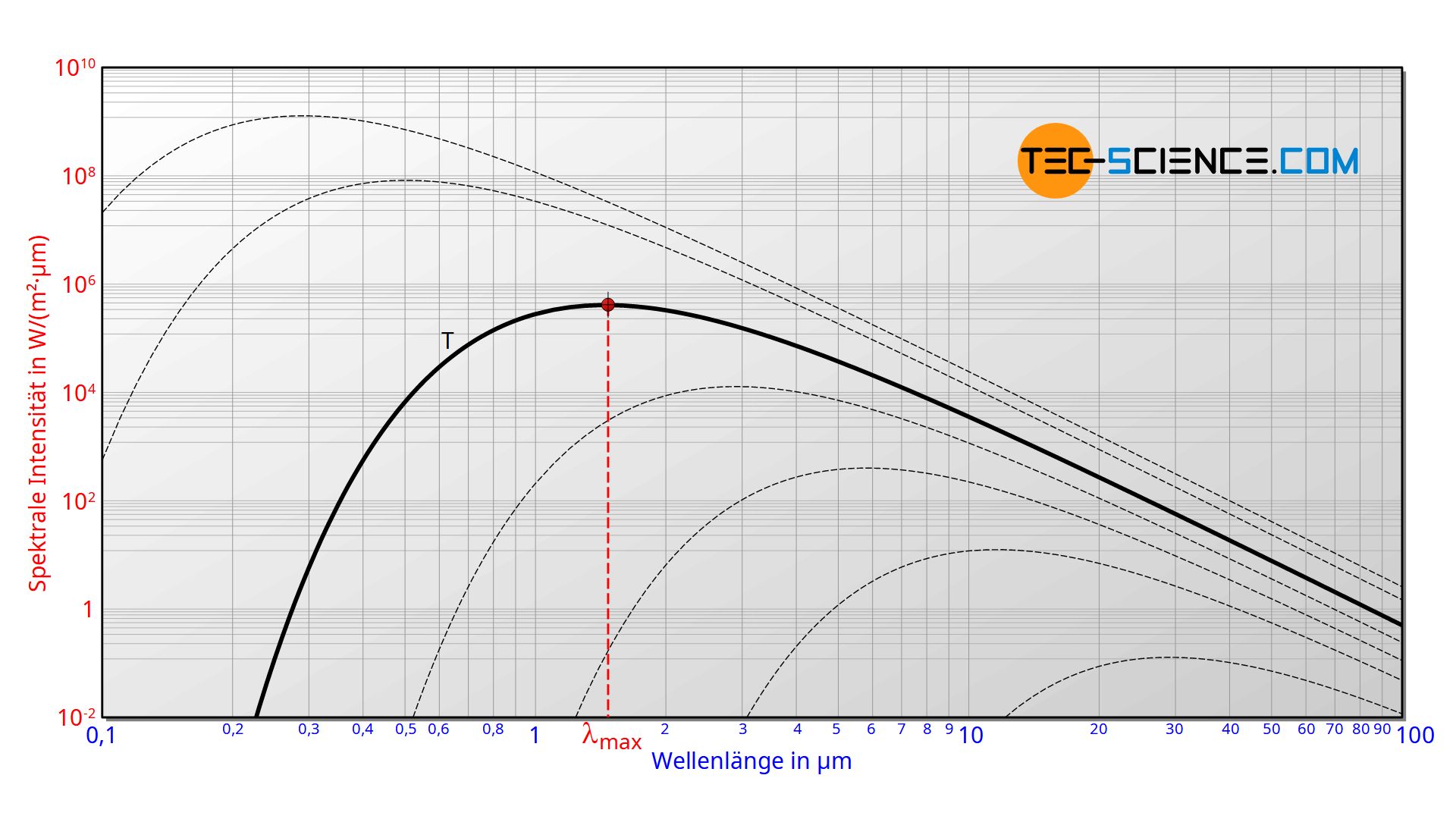
Das ausgesendete Wellenlängenspektrum der Schwarzkörperstrahlung wie es die untere Abbildung zeigt konnte lange Zeit nicht erklärt werden. Bis dahin ging man nämlich immer von einer kontinuierlichen Verteilung der Energie aus. Erst durch Einführung diskreter Energiezustände gelang es dem Physiker Max Planck die Schwarzkörperstrahlung mathematisch zu beschreiben. Obwohl er die Einführung diskreter Energien physikalisch zunächst nicht zu deuten wusste, legte er damit den Grundstein der Quantenmechanik.

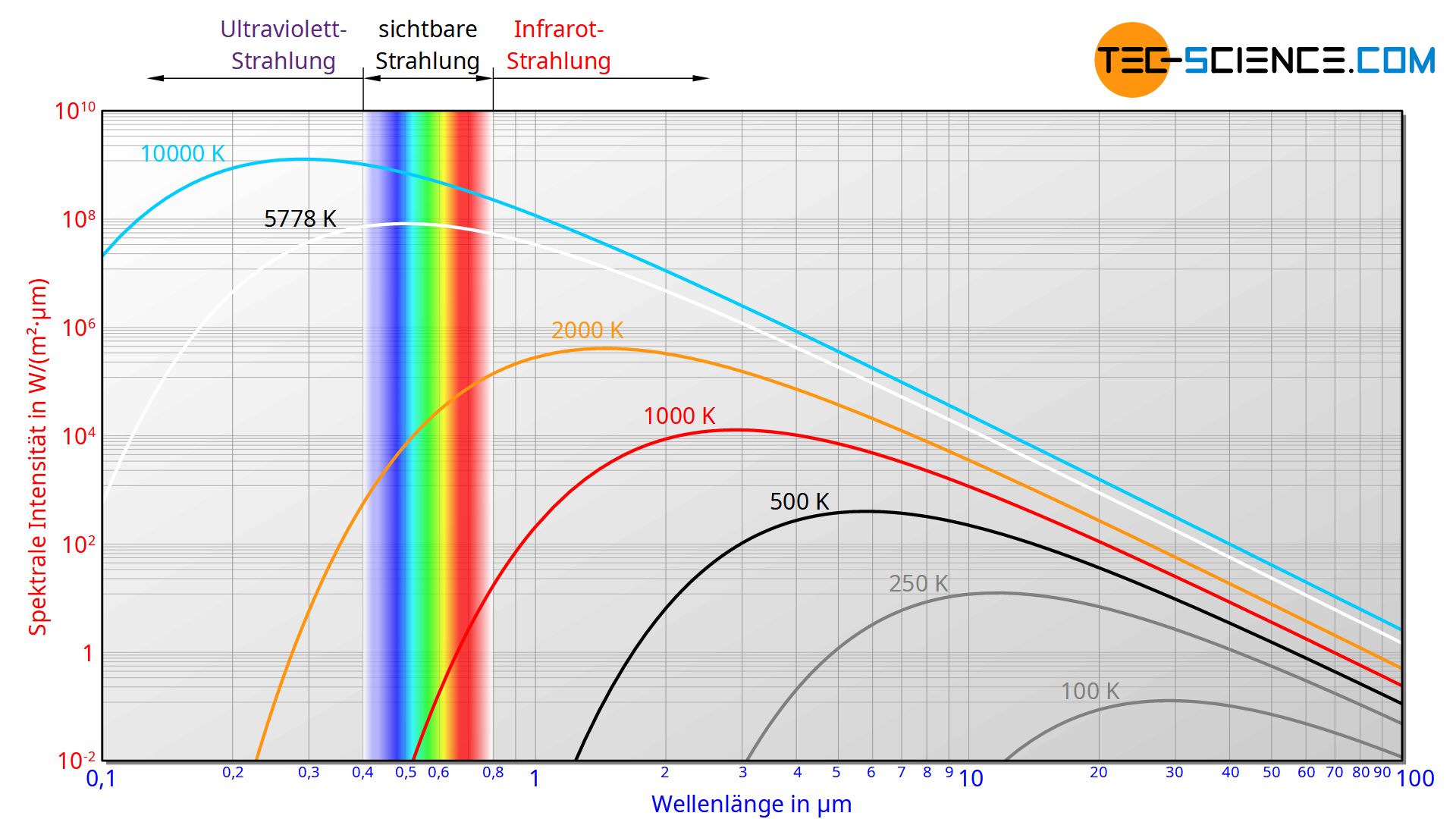
Max Planck konnte die unten angegebene Formel herleiten, die die spektrale Intensität I_s in Abhängigkeit der Wellenlänge λ wiedergibt. Diese Formel ist auch als Planck’sches Strahlungsgesetz bekannt.

\begin{align}
\label{planck}
&\boxed{I_s(\lambda) = \frac{2\pi h c^2}{\lambda^5} \cdot \frac{1}{\exp\left(\dfrac{h c}{\lambda k_B T}\right)-1} } ~~~\text{Planck’sches Strahlungsgesetz} \\[5px]
\end{align}

Die Intensität meint darin die pro Flächeneinheit abgegebene Strahlungsleistung des schwarzen Körpers (Flächenleistungsdichte). Wird die Intensität wie in diesem Fall zusätzlich noch auf das Wellenlängeintervall bezogen innerhalb dessen die Leistung emittiert wird, so spricht man von der spektralen Intensität. Wird die spektrale Intensität über die Wellenlänge aufgetragen, so entspricht in einem solchen Diagramm die Fläche unter der Kurve der abgestrahlten Intensität im betrachteten Wellenlängenbereich.

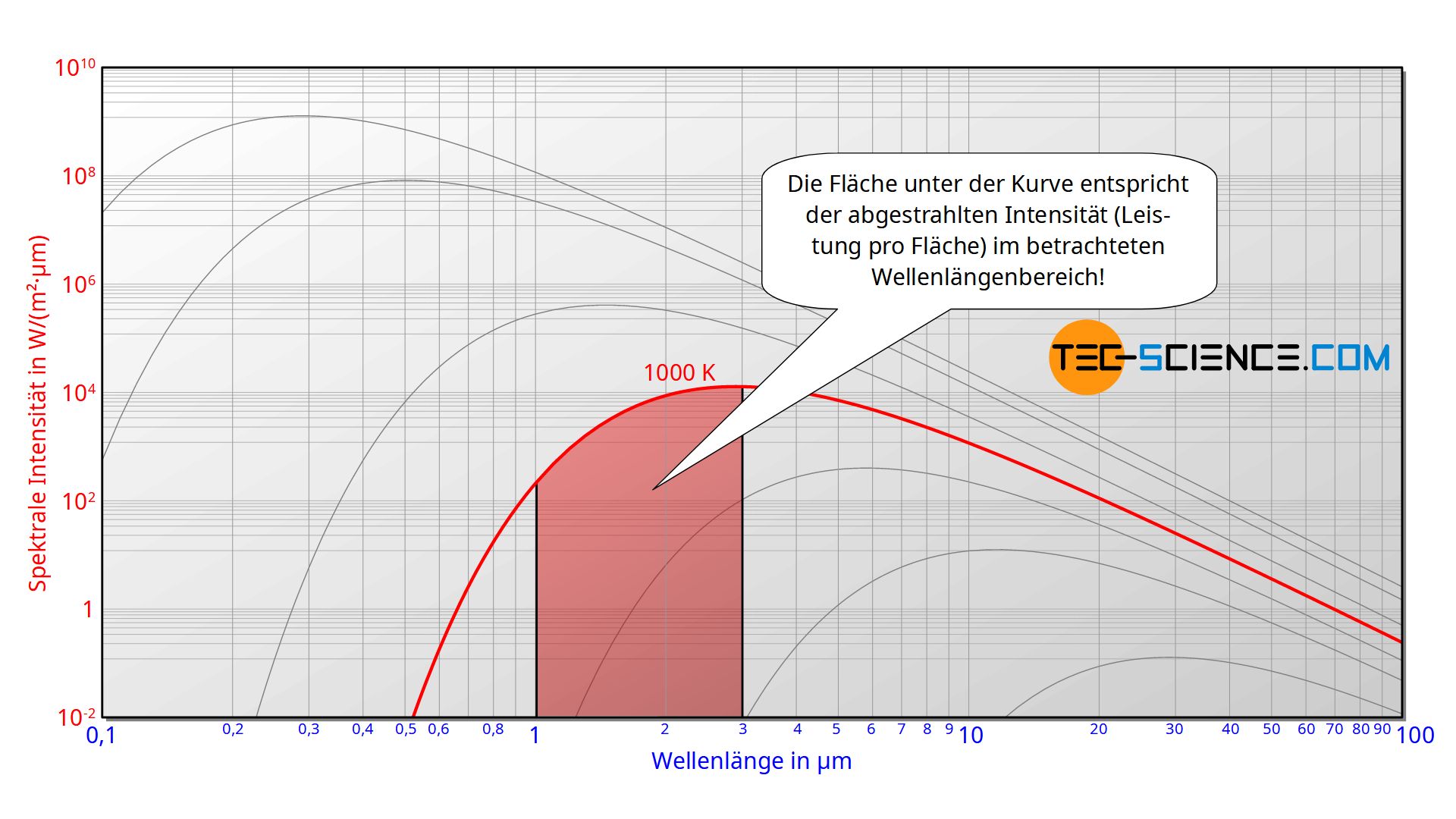
Zwischen der Wellenlänge λ einer Strahlung und dessen Frequenz f besteht ein fester Zusammenhang. Dieser ergibt sich über die Ausbreitungsgeschwindigkeit der Strahlung, die in diesem Fall der Lichtgeschwindigkeit c entspricht (c=λ⋅f). Deshalb lässt sich die spektrale Verteilung der Intensität I_s auch in Abhängigkeit der Frequenz ausdrücken:

\begin{align}
\label{freq}
&\boxed{I_s(f) = \frac{2\pi h f^3}{c^2} \cdot \frac{1}{\exp\left(\dfrac{h f}{k_B T}\right)-1} } ~~~\text{Planck’sches Strahlungsgesetz} \\[5px]
\end{align}

Im Artikel Unterschiedliche Formen des Planck’schen Strahlungsgesetzes wird auf die Herleitung dieser Frequenzdarstellung aus der Wellenlängendarstellung und auf weitere Formen des Planck’schen Strahlungsgesetzes näher eingegangen.

Stefan-Boltzmann-Gesetz

Wie bereits erwähnt, ergibt sich die abgestrahlte Intensität als Fläche unter der spektralen Intensitätsverteilung. Hierzu ist das Planck’schen Strahlungsgesetz folglich über den gesamten Wellenlängenbereich bzw. Frequenzbereich hinweg zu integrieren. An dieser Stelle soll die Integration anhand der Frequenzdarstellung nach Gleichung (\ref{freq}) erfolgen:

\begin{align}
&I= \int_{0}^{\infty} I_s(f) ~ \text{d}f\\[5px]
&I= \int_{0}^{\infty} \frac{2\pi h f^3}{c^2} \cdot \frac{1}{\exp\left(\dfrac{h f}{k_B T}\right)-1} ~ \text{d}f\\[5px]
\label{her}
&I= \frac{2\pi h}{c^2} \cdot \int_{0}^{\infty} \frac{f^3}{\exp\left(\dfrac{hf }{k_B T}\right)-1} ~ \text{d}f\\[5px]
\end{align}

Diese Integral kann man dadurch lösen, dass man zunächst das Argument der Exponentialfunktion h⋅f/(k_B⋅T) durch x ersetzt (Integration durch Substitution). Somit gelten folgende Beziehungen zwischen der neu definierten Variablen x und der bisherigen Variablen f:

\begin{align}
&x := \frac{hf}{k_B T} ~~~\Rightarrow \boxed{\color{red}{f = \frac{x k_B T}{h}}} \\[5px]
&\frac{\text{d}x}{\text{d}f} = \frac{h}{k_B T} ~~~\Rightarrow \boxed{\color{blue}{\text{d}f = \frac{k_B T}{h}\text{d}x} } \\[5px]
\end{align}

Werden diese Beziehungen in Gleichung (\ref{her}) eingesetzt, dann gilt:

\begin{align}
&I= \frac{2\pi h}{c^2} \cdot \int_{0}^{\infty} \frac{\left(\color{red}{\frac{x k_B T}{h} }\right)^3}{\exp\left(\color{red}{x} \right)-1} ~ \color{blue}{\frac{k_B T}{h}\text{d}x }\\[5px]
&I= \frac{2\pi h}{c^2} \cdot \int_{0}^{\infty} \frac{k_B^3 T^3}{h^3} \frac{x^3}{\exp\left(x \right)-1} ~ \frac{k_B T}{h}\text{d}x\\[5px]
&I= \frac{2\pi h}{c^2} \cdot \frac{k_B^3 T^3}{h^3} \cdot \frac{k_B T}{h} \cdot \int_{0}^{\infty} \frac{x^3}{\exp\left(x \right)-1} ~\text{d}x\\[5px]
&I= \frac{2\pi k_B^4}{h^3 c^2} T^4 \int_{0}^{\infty} \frac{x^3}{\exp\left(x \right)-1} ~\text{d}x\\[5px]
\end{align}

Das Integral ∫₀^∞ x³/(exp(x)-1) dx lässt sich auf herkömmliche Weise nicht so einfach lösen. Ein Blick in die Formelsammlung der Mathematik liefert aber als Ergebnis den Wert π⁴/15. Somit gilt für die abgestrahlte Intensität eines Schwarzen Körpers:

\begin{align}
&I= \frac{2\pi k_B^4}{h^3 c^2} T^4 \cdot \frac{\pi^4}{15}\\[5px]
&I= \underbrace{\frac{2\pi^5 k_B^4}{15 h^3 c^2}}_{\sigma} \cdot T^4 \\[5px]
&\boxed{I= \sigma \cdot T^4}~~~~~\text{mit}~~~~~\boxed{\sigma = \frac{2\pi^5 k_B^4}{15 h^3 c^2}}= 5,670 \cdot 10^{-8} \frac{\text{W}}{\text{m²K}^4} \\[5px]
\end{align}

Die konstanten Größen in der oberen Gleichung können zu einer neuen Konstante zusammengefasst werden. Diese neue Konstante wird Stefan-Boltzmann-Konstante σ genannt (nicht zu verwechseln mit der Boltzmann-Konstanten k_B!). Die abgestrahlte Intensität eines Schwarzen Körpers ist also nur von der Temperatur abhängig. Sie nimmt mit der vierten Potenz der Temperatur zu. Diese Gesetzmäßigkeit wird auch als Stefan-Boltzmann-Gesetz bezeichnet.

Das Stefan-Boltzmann-Gesetz besagt, dass die Strahlungsintensität eines Schwarzen Körpers im thermischen Gleichgewicht proportional zur vierten Potenz der Temperatur ist!

Mithilfe der Intensität I kann nun auch die Strahlungsleistung Φ eines Schwarzen Körpers ermittelt werden, d.h. die insgesamt pro Zeiteinheit abgegebene Strahlungsenergie. Hierzu ist die Intensität I (als Flächenleistungsdichte) lediglich mit der Oberfläche A des Schwarzen Körpers zu multiplizieren:

\begin{align}
&\boxed{\Phi(T,A) = \sigma \cdot A \cdot T^4} \\[5px]
\end{align}

Mehr Informationen zum Stefan-Boltzmann-Gesetz und zur Herleitung aus der Thermodynamik finden sich im Hauptartikel Stefan-Boltzmann-Gesetz wieder.

Reale Körper: Der Emissionsgrad

In der Praxis strahlen reale Gegenstände nicht mit der Intensität eines Schwarzen Körpers sondern haben eine geringere Strahlungsleistung. Dies wird durch den einheitenlosen Emissionsgrad ε<1 ausgedrückt. Der Emissionsgrad gibt die Strahlungsleistung eines realen Körpers im Vergleich zu einem idealen Schwarzen Körper wieder:

\begin{align}
&\boxed{I_{real}=\varepsilon \cdot \sigma \cdot T^4}\\[5px]
&\boxed{\Phi_{real} = \varepsilon \cdot \sigma \cdot A \cdot T^4} \\[5px]
\end{align}

Für nicht-metallische Oberflächen liegt der Emissionsgrad in vielen Fällen über 0,9. Diese Gegenstände können im Hinblick auf die emittierte Strahlung somit in sehr guter Näherung als Schwarze Körper betrachtet werden. Dies macht die Temperaturbestimmung von realen Gegenständen mit Hilfe einer Wärmebildkamera oder einem Pyrometer relativ einfach, da Oberflächeneigenschaften einen eher untergeordneten Einfluss haben (sofern die Oberflächen nicht extrem reflektierend sind).

Wiensches Verschiebungsgesetz

Die spektrale Intensitätsverteilung in Abhängigkeit der Temperatur soll nun genauer betrachtet werden. Es zeigt sich, dass sich das Maximum der Kurve mit zunehmender Temperatur zu immer geringeren Wellenlängen verschiebt. Die Abhängigkeit dieser Wellenlänge λ_max von der Temperatur ist durch nachfolgende Gleichung gegeben. Diese Gleichung ist auch als Wiensches Verschiebungsgesetz bekannt.

\begin{align}
&\boxed{\lambda_{max}=\frac{2897,8 \text{ µm K}}{T}}~~~\text{Wiensches Verschiebungsgesetz} \\[5px]
\end{align}

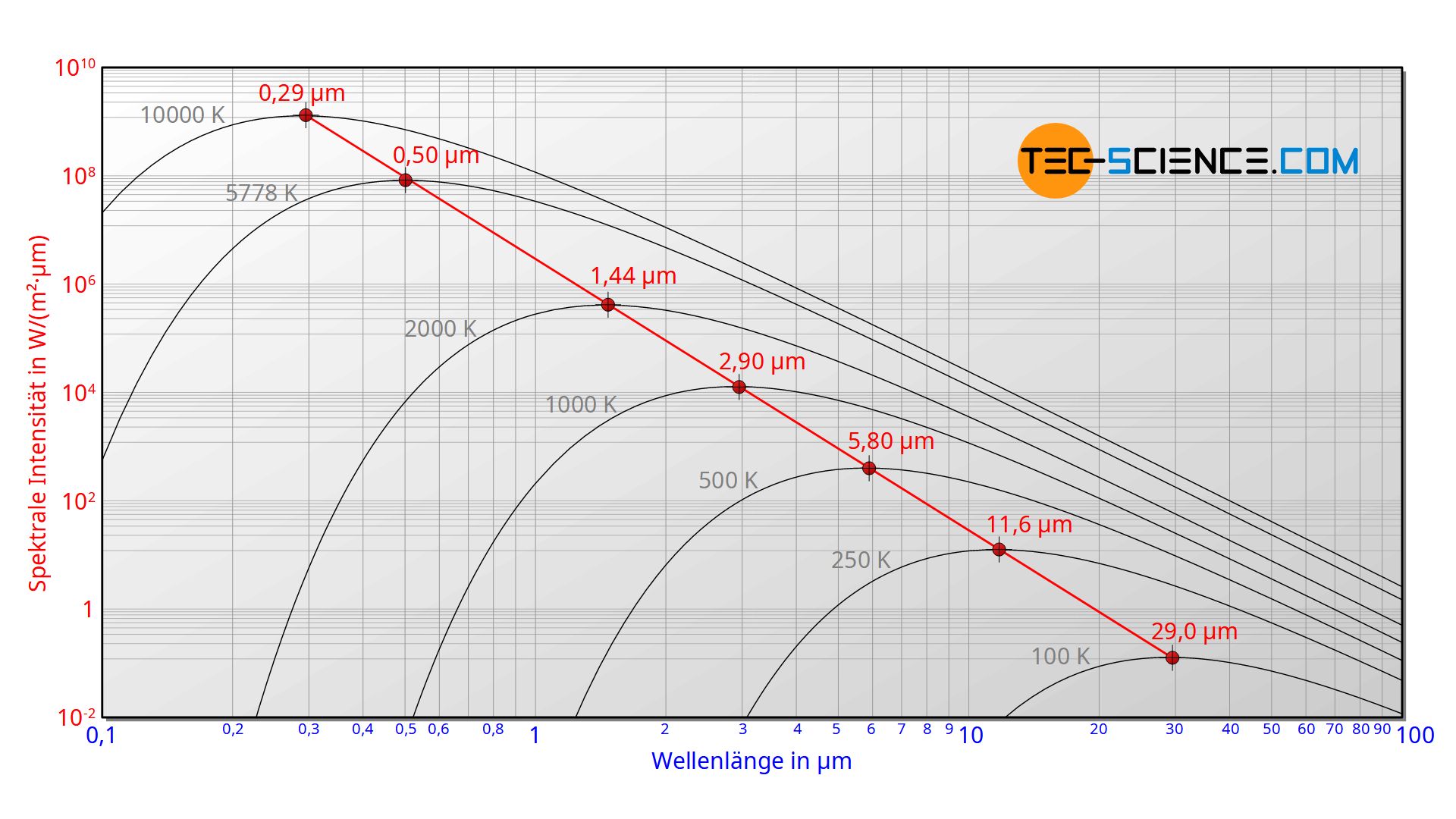
Man kann das Wiensche Verschiebungsgestz durch Bestimmung des Hochpunktes der Planckschen Strahlungsfunktion (\ref{planck}) ermitteln. Hierfür muss die Funktion unter Zuhilfenahme der Produktregel lediglich nach der Wellenlänge λ abgeleitet und Null gesetzt werden:

\begin{align}
\label{abl}
&\frac{\text{d}I_s(\lambda)}{\text{d}\lambda} \overset{!}{=} 0 ~~~~~\text{mit}~~~~~ I_s(\lambda) = \frac{2\pi h c^2}{\lambda^5} \cdot \frac{1}{\exp\left(\dfrac{h c}{\lambda k_B T}\right)-1} \\[5px]
\end{align}

\begin{align}
\frac{\text{d}I_s(\lambda)}{\text{d}\lambda} &= 2 \pi c^2 \left(\frac{hc}{k_B T \lambda^7} \cdot \frac{\exp\left( \frac{hc}{k_B T \lambda}\right)}{\left[\exp\left( \frac{hc}{k_B T \lambda} \right) -1\right]^2} – \frac{1}{\lambda^6} \cdot \frac{5}{\exp\left(\frac{hc}{k_B T \lambda}\right)-1} \right) \\[5px]
&= \underbrace{\frac{2 \pi c^2}{\lambda^6 \cdot \left[ \exp\left( \frac{hc}{k_B T \lambda} \right) -1 \right] }}_{>0} \underbrace{\left(\frac{hc}{k_B T \lambda} \cdot \frac{\exp\left( \frac{hc}{k_B T \lambda}\right)}{\exp\left( \frac{hc}{k_B T \lambda} \right) -1} – 5 \right)}_{=0} =0
\end{align}

Diese Gleichung wird nur dann null sein, wenn der Ausdruck in der runden Klammer null wird. Somit folgt:

\begin{align}
&\frac{hc}{k_B T \lambda} \cdot \frac{\exp\left( \frac{hc}{k_B T \lambda} \right)}{\exp\left( \frac{hc}{k_B T \lambda} \right) -1} – 5 = 0 \\[5px]
\end{align}

Mit der nachfolgend angegebenen Substitution, vereinfacht sich diese Gleichung wie folgt:

\begin{align}
\label{max}
&\boxed{x := \frac{hc}{\lambda k_B T}} ~~~\Rightarrow~~~ x \cdot \frac{\exp\left(x\right)}{\exp\left(x\right) -1} – 5 = 0 \\[5px]
\end{align}

Diese Gleichung kann nur numerisch gelöst werden, z.B. mit dem Newton-Verfahren. Als Lösung erhält man x = 4,9651. Mit dieser Lösung kann die Wellenlänge λ_max nun bestimmt werden. Hierzu muss Gleichung (\ref{max}) lediglich nach der gesuchten Variablen λ_max umgestellt werden:

\begin{align}
& \lambda_{max}= \frac{hc}{x k_B T} = \frac{\tfrac{hc}{x k_B}}{T}= \frac{0,0028978 \text{ m K}}{T}= \frac{2897,8 \text{ µm K}}{T} \\[5px]
\end{align}

\begin{align}
&\boxed{\lambda_{max}=\frac{2897,8 \text{ µm K}}{T}}\\[5px]
\end{align}

Das Maximum der spektralen Intensität kann auch für die Frequenzdarstellung I_s(f) ermittelt werden. Hierfür ist die Funktion I_s(f) nach der Frequenz f abzuleiten und anschließend Null zu setzen:

\begin{align}
&\frac{\text{d}I_s(f)}{\text{d}\lambda} \overset{!}{=} 0 ~~~\Rightarrow~~~ \boxed{f_{max} = 5,879 \cdot 10^{10} \tfrac{\text{Hz}}{\text{K}} \cdot T}
\end{align}

Anmerkung

Beachte, dass das Wiensche Verschiebungsgesetz die Wellenlänge λ_max angibt bei der die spektrale Intensität ein Maximum aufweist. Dieses Maximum ist nicht gleichzusetzen mit dem Maximum der Intensität an sich bzw. mit dem Maximum der Strahlungsleistung! Dies führt zum Beispiel dazu, dass zwar der allgemeine Zusammenhang f=c/λ gilt, jedoch in diesem speziellen Fall nicht f_max=c/λ_max!

Dies hat damit zu tun, dass es sich bei der spektralen Intensität um eine auf die Wellenlänge bezogene Größe handelt. Man misst sozusagen die Strahlungsleistung in einem bestimmten Wellenlängenbereich dλ und bezieht hierauf die Strahlungsleistung. Ein Vergleich unterschiedlicher Strahlungsleistungen ist also nur dann gegeben wenn auch immer dieselben Wellenlängenintervalle betrachtet werden. Da die Frequenz nun nicht proportional zur Wellenlänge ist sondern umgekehrt proportional, bedeuten äquidistante Wellenlängenintervalle nicht auch äquidistante Frequenzintervalle.

Als einfaches Beispiel soll der Wellenlängenbereich zwischen 1 und 10 µm dienen, der in Intervallen von jeweils 1 µm unterteilt wird. Es ergibt sich somit die folgende äquidistante Reihe:

\begin{align}
&1-2-3-4-5-6-7-8-9-10 \\[5px]
\end{align}

Die reziproken Werte hiervon, die im übertragenen Sinne die Bedeutung der Frequenz als reziproker Wert der Wellenlänge haben, ergeben aber keine äquidistante Reihe mehr:

\begin{align}
&\frac{1}{1}-\frac{1}{2} -\frac{1}{3} -\frac{1}{4} -\frac{1}{5} -\frac{1}{6} -\frac{1}{7} -\frac{1}{8} -\frac{1}{9} -\frac{1}{10} \\[5px]
&1-0,5-0,333-0,25-0,2-0,167-0,143-0,125-0,111-0,1 \\[5px]
\end{align}

Man kann also äquidistante Wellenlängenintervalle nicht mit äquidistanten Frequenzintervallen vergleichen kann. Deshalb gilt in der Frequenzdarstellung der spektralen Intensität eine andere Frequenz f_max als man durch die Formel f_max=c/λ_max erwarten könnte.