Der Strahlungsdruck kommt durch den Impulsübertrag der Photonen zustande, wenn diese mit Materie treffen.
Einleitung
Trifft Licht auf einen Gegenstand, dann übt diese Strahlung eine bestimmte Kraft auf diesen Gegenstand aus und in Bezug auf die auftreffende Fläche auch einen gewissen Druck, den sogenannten Strahlungsdruck.

Im Teilchenmodell ist das Zustandekommen dieses Drucks relativ einfach nachvollziehbar. Gemäß der Quantenmechanik kann man sich jede ausbreitende Welle auch als Strahl von Teilchen vorstellen (Welle-Teilchen-Dualismus). Die einzelnen Lichtteilchen werden dann auch Photonen genannt.
Als Photonen bezeichnet man in der Quantentheorie die Lichtteilchen die die elektromagnetische Strahlung ausmachen!

Jedes Photon trägt sowohl Energie als auch einen Impuls. Treffen die Photonen aus der Strahlung nun mit bestimmter Energie bzw. bestimmtem Impuls auf einen Gegenstand, dann üben diese beim Aufprall eine Stoßkraft aus, analog zu Tennisbällen, die gegen eine Wand geworfen werden.
Der Strahlungsdruck ist auch der Grund weshalb der Schweif von Kometen immer von der Sonne weggerichtet ist, unabhängig der Flugrichtung. Unter atmosphärischen Bedingungen würden normalerweise die sich ablösenden Gas- und Staubteilchen eines Kometen vom Luftwiderstand abgebremst werden. Der aus den sich abgelösten Teilchen bildende Schweif würde sich somit stets entgegen der Flugrichtung ausbilden. Im Vakuum des Weltalls gibt es jedoch keinen Luftwiderstand. Als einzige Kraft wirkt nur der Strahlungsdruck der Sonne (nicht zu verwechseln mit dem Sonnenwind). Die Photonen der Sonnenstrahlung „blasen“ den Schweif somit immer von der Sonne weg.

Der Strahlungsdruck kann theoretisch auch als alternative Antriebstechnologie für Flüge im Weltraum genutzt werden. Mit sogenannten Sonnensegeln wird die Kraft der Strahlung analog zur Windkraft bei Windsegeln für den Antrieb genutzt. Die Kraft der Strahlung ist zwar relativ gering, aufgrund der fehlenden Luftreibung im Weltall kann dies über einen längeren Zeitraum hinweg jedoch zu einer enormen Geschwindigkeit führen. Diese Antriebstechnologie eignet sich deshalb besonders für kleine Sonden und Satelliten, die sehr große Distanzen zwischen Planeten zurücklegen. Ein solcher Strahlungsantrieb ist aktuell noch Gegenstand der Forschung.

Herleitung
Energie der Photonen
Die Kraft die die Photonen beim Aufprall auf eine Fläche \(\Delta A\) ausüben, ist abhängig vom Impuls der Photonen. Der Impuls lässt sich dabei über die Energie der Photonen berechnen. Die Energie eines Photons \(W_p\) wiederum ergibt sich über die Frequenz der Strahlung \(f\) bzw. über deren Wellenlänge \(\lambda\):
\begin{align}
\label{w}
&W_p = h \cdot f = h \cdot \frac{\lambda}{c} \\[5px]
\end{align}
Darin bezeichnet \(h\) das Plancksches Wirkungsquantum und \(c\) die Ausbreitungsgeschwindigkeit der elektromagnetischen Strahlung (Lichtgeschwindigkeit).
Impuls der Photonen
Über die Definition des Impulses als Produkt von Masse und Geschwindigkeit (\p=m \cdot v\)) sowie der berühmten Formel zur Masse-Energie-Äquivalenz von Einstein (\(E=m \cdot c^2\)), kann ein Zusammenhang zwischen Impuls und Energie für Photonen hergeleitet werden.
Die Energie \(E\) in Einsteins Formel entspricht dabei der Energie \(W_p\) eines Photons und die Geschwindigkeit \(v\) in der Formel für den Impuls, der Lichtgeschwindigkeit des Photons \(c\) (\(m\) steht in diesem Fall für die relativistische Masse des Photons).
\begin{align}
p &=m \cdot c &&~~~~~\text{Impuls eines Photons}\\[5px]
W_p &=m \cdot c^2 &&~~~~~\text{Masse-Energie-Äquivalenz eines Photons}\\[5px]
\end{align}
Teilt man die oberen Gleichungen durcheinander, dann ergibt sich folgender Zusammenhang zwischen dem Impuls und der Energie eins Photons:
\begin{align}
&\frac{p}{W_p}=\frac{m \cdot c}{m \cdot c^2} = \frac{1}{c} \\[5px]
& p = \frac{W_p}{c} \\[5px]
\end{align}
Auf dieselbe Gleichung gelangt man auch mithilfe des Energie-Impuls-Zusammenhangs aus der Relativitätstheorie:
\begin{align}
&W_p = \sqrt{(p \cdot c)^2+ (m_0 \cdot c)^2} ~~~~~\text{Energie-Impuls-Relation}\\[5px]
\end{align}
Da Photonen sich mit Lichtgeschwindigkeit bewegen und somit offensichtlich keine Ruhemasse besitzen können (\(m_0\)= 0), zeigt sich an dieser Stelle derselbe Zusammenhang zwischen Energie und Impuls:
\begin{align}
&W_p = p \cdot c \\[5px]
& p = \frac{W_p}{c} \\[5px]
\end{align}
Strahlungsdruck bei vollständiger Absorption
Im Folgenden wird die Formel zur Berechnung des Strahlungsdrucks hergeleitet. Dabei wird zunächst davon ausgegangen, dass der Gegenstand die auftreffende Strahlung vollständig absorbiert.

Treffen aus der gesamten Strahlung innerhalb einer gewissen Zeit \(\Delta t\) insgesamt \(\Delta N\) Teilchen auf die Fläche \(\Delta A\) des betrachteten Gegenstandes, dann ergibt sich folgender Gesamtimpuls \(p_{ges}\) für die betrachteten Teilchen:
\begin{align}
&p_{ges} = p \cdot \Delta N = \frac{W_p}{c} \cdot \Delta N = W_p \cdot \Delta N \cdot \frac{1}{c} \\[5px]
\end{align}

In der oberen Gleichung kann ausgenutzt werden, dass das Produkt aus Photonenenergie \(W_p\) und Photonenanzahl \(\Delta N\) der Energiemenge \(\Delta W\) entspricht, die innerhalb der Zeit \(\Delta t\) insgesamt auf die Fläche \(\Delta A\) trifft:
\begin{align}
&p_{ges} = \overbrace{W_p \cdot \Delta N }^{=\Delta W} \cdot \frac{1}{c} =\Delta W \cdot \frac{1}{c} \\[5px]
\end{align}
Aufgrund der Impulserhaltung bleibt dieser Gesamtimpuls auch nach dem Aufprall auf den zunächst ruhenden Gegenstand vollständig erhalten. Wird davon ausgegangen, dass alle Photonen beim Aufprall absorbiert werden, dann muss folglich dieser Gesamtimpuls vollständig auf den Gegenstand übertragen werden. Aus der Impulsänderung des Gegenstandes \(\Delta p\), welcher demzufolge dem Gesamtimpuls \(p_{ges}\) der Teilchen entspricht, lässt sich die ausgeübte Kraft \(F_{ges}\) auf den Gegenstand als Impulsänderung pro Zeit ermitteln:
\begin{align}
&F_{ges} = \frac{\Delta p}{\Delta t} = \frac{p_{ges}}{\Delta t} = \frac{\Delta W \cdot \frac{1}{c}}{\Delta t} = \frac{\Delta W}{\Delta t} \cdot \frac{1}{c} \\[5px]
\end{align}
In der oberen Gleichung kann der Quotient aus Energie und Zeit als Strahlungsleistung \(\Phi_{St}\) aufgefasst werden, d.h. als Energiemenge die pro Zeit auf die Fläche \(\Delta A\) trifft:
\begin{align}
&F_{ges} = \overbrace{\frac{\Delta W}{\Delta t}}^{\Phi_{St}} \cdot \frac{1}{c} = \Phi_{St} \cdot \frac{1}{c} \\[5px]
\end{align}
Da diese Kraft \(F_{ges}\) auf die Fläche \(\Delta A\) wirkt, lässt sich schließlich der entsprechende Druck berechnen, den der auftreffende Teilchenstrom mit der Leistung \(\Phi_{St}\) verursacht. Dieser Druck wird auch Strahlungsdruck \(p_{St}\) genannt (nicht zu verwechseln mit dem Photonenimpuls \(p\)!):
\begin{align}
\label{ww}
&p_{St} = \frac{F_{ges}}{\Delta A} =\frac{\Phi_{St}}{\Delta A} \cdot \frac{1}{c} \\[5px]
\end{align}
Der Quotient aus auftreffender Strahlungsleistung \(\Phi_{St}\) und zugehöriger Fläche \(\Delta A\) wird auch Intensität oder Bestrahlungsstärke genannt, da diese Größe ein anschauliches Maß dafür ist, wie stark eine Fläche mit Energie bestrahlt wird (Flächenleistungsdichte). Zwischen der Intensität \(I\) und dem Strahlungsdruck gilt also ein relativ einfacher Zusammenhang:
\begin{align}
&\boxed{p_{St} =\frac{I}{c}} ~~~~~\text{gilt nur für vollständige Absorption} \\[5px]
\end{align}
Als Intensität oder Bestrahlungsstärke bezeichnet man die flächenbezogene Strahlungsleistung (Flächenleistungsdichte)!
Strahlungsdruck bei vollständiger Reflexion
Beachte, dass der oben beschriebene Zusammenhang zwischen dem Strahlungsdruck und der Intensität nur gilt, wenn die Strahlung beim Auftreffen auf den Gegenstand vollständig absorbiert wird!
Wird die Strahlung hingegen vollständig reflektiert, dann entfernen sich die Photonen nach dem Aufprall wieder mit betragsmäßig demselben Impuls, jedoch in die reflektierte Richtung. Damit der Gesamtimpuls nach wie vor erhalten ist, musste der Gegenstand nun eine doppelt so große Impulsänderung erfahren. Dementsprechend wirkt auf den reflektierenden Gegenstand bei gleicher Intensität dann auch ein doppelt so großer Strahlungsdruck!
\begin{align}
&\boxed{p_{St} =2 \frac{I}{c}} ~~~~~\text{gilt nur bei vollständiger Reflexion} \\[5px]
\end{align}
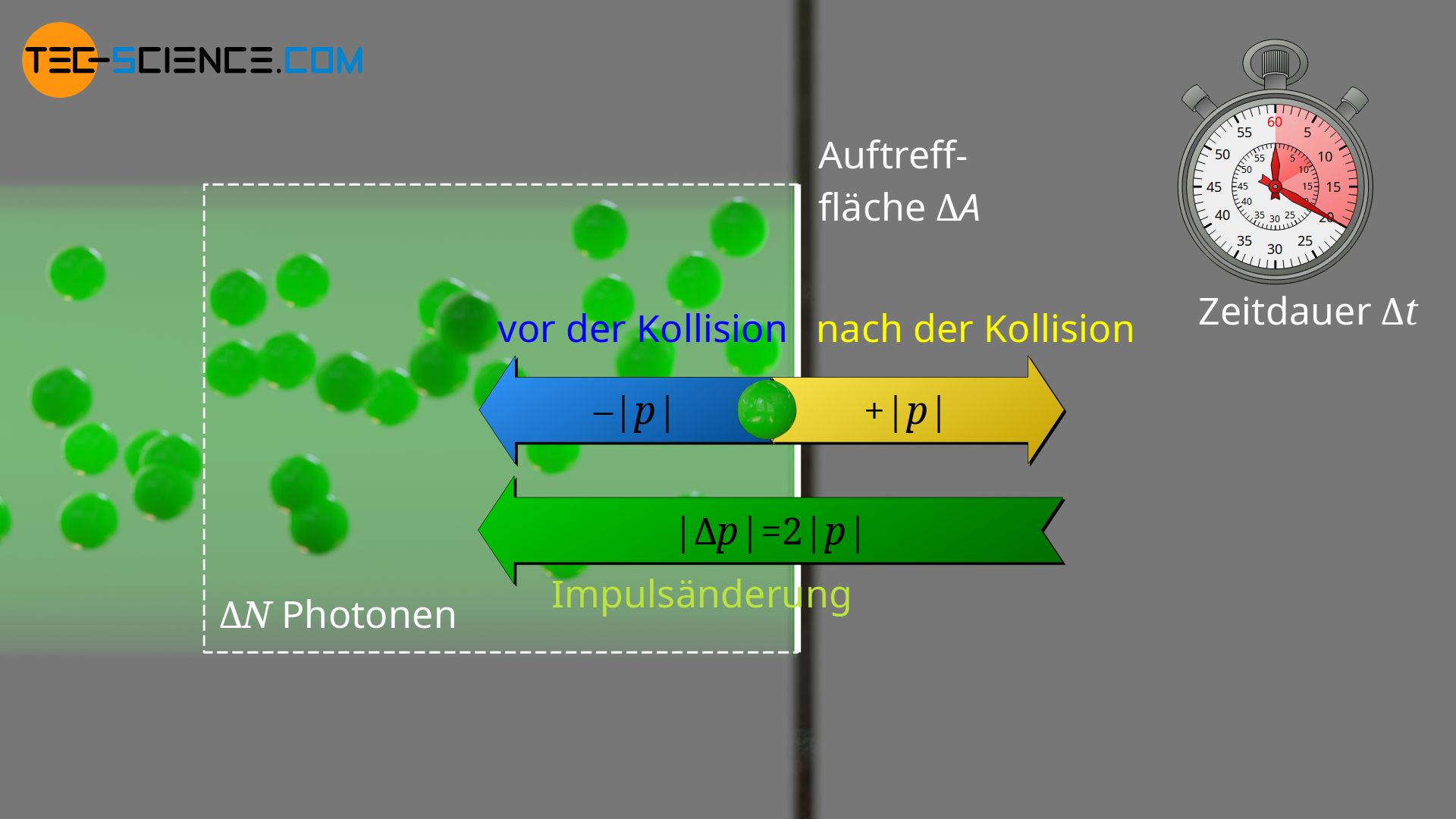
Der Strahlungsdruck auf eine ideal reflektierende Fläche ist doppelt so groß wie auf eine ideal absorbierende Fläche!
Dass der Strahlungsdruck bei Reflexion doppelt so groß ist wie bei Absorption, lässt sich auch auf anschauliche Weise nachvollziehen. Als analoges Beispiel wird hierzu eine Person betrachtet, die auf einem reibungsfrei gleitenden Skateboard steht. Wird dieser Personen nun ein schwerer Medizinball zugeworfen, dann wird beim Fangen des Balls der Impuls auf die Person mitsamt Skateboard übertragen. Dieses Fangen des Balls entspricht im übertragenen Sinne der vollständigen Absorption der Photonen.
Aber nicht nur durch ein Zuwerfen und Fangen des Balls kann die Person in Bewegung gesetzt werden, sondern auch durch ein Wegwerfen. Beim Wegwerfen stößt sich die Person in gewisser Weise vom Medizinball ab und bekommt hierdurch ebenfalls einen Impuls („Raketenprinzip“).
Wenn also die Person einen Medizinball zugeworfen bekommt und diesen anschließend wieder von sich wegwirft, dann hat sie dies in doppelter Hinsicht genutzt. Sie bekommt nicht nur einen Impuls durch das Fangen sondern erzeugt zusätzlich einen Impuls durch das anschließende Wegwerfen. Wird der Ball dabei mit derselben (relativen) Geschwindigkeit wieder abgeworfen wie er gefangen wurde, dann hat die Person im Vergleich zum reinen „Absorbieren“ des Balls den doppelten Impuls auf sich übertragen können (doppelte Kraft).
Macht man nun in Gedanken das Fangen und Abwerfen immer schneller und schneller, dann handelt es sich kinematisch betrachtet letztlich um ein reines Abprallen des Balles an der Person, d.h. um eine Reflexion! Die Reflexion erzeugt also einen doppelt so großen Impuls im Vergleich zu einer Absorption.
Zusammenhang zwischen Strahlungsdruck und Energiedichte
Gerichtete Strahlung (Photonenstrahl)
An dieser Stelle soll Gleichung (\ref{ww}) noch in anderer Hinsicht interpretiert werden. Wird die Ausbreitungsgeschwindigkeit der Welle \(c\) (Lichtgeschwindigkeit) durch die zurückgelegte Wegstrecke \(\Delta s\) innerhalb der Zeit \(\Delta t\) ausgedrückt, dann gilt:
\begin{align}
&p_{St} = \frac{\Phi_{St}}{\Delta A} \cdot \frac{1}{c} = \frac{\Phi_{St}}{\Delta A} \cdot \frac{1}{\frac{\Delta s}{\Delta t}} = \frac{\overbrace{\Phi_{St}\cdot \Delta t}^{\Delta W}}{\underbrace{\Delta A \cdot \Delta s}_{\Delta V}} =\frac{\Delta W}{\Delta V} = w \\[5px]
&\boxed{p_{St} = w} ~~~~~\text{gilt nur bei vollständiger Absorption}
\end{align}

In der oberen Gleichung wurde ausgenutzt, das das Produkt aus Leistung und Zeit der Energie der Strahlung \(\Delta W\) entspricht, die im Raumvolumen \(\Delta V\) beinhaltet ist und die dann den entsprechenden Strahlungsdruck \(p_{St}\) ausübt. Der Quotient von Strahlungsenergie und Volumen wird auch als Energiedichte \(w\) bezeichnet und gibt die in einem Raumvolumen enthaltene Strahlungsenergie wieder.
Wie diese Gleichung folglich zum Ausdruck bringt, lässt sich der Strahlungsdruck auch als Energiedichte auffassen! Dieser direkte Zusammenhang zwischen volumetrischer Energiedichte und Strahlungsdruck gilt wiederum nur bei vollständiger Absorption der Strahlung, wenn diese auf den Gegenstand trifft!
Zudem muss die Strahlung in diesem Fall senkrecht auf die absorbierende Fläche treffen. Ist die Fläche bspw. parallel zur Strahlung gerichtet, dann prallen die Photonen offensichtlich nicht auf die Fläche. Es wird folglich auch kein Strahlungsdruck ausgeübt, obwohl die Strahlung natürlich nach wie vor eine Energie und damit eine Energiedichte besitzt (die Energie trifft sozusagen nicht auf die Fläche sondern „fliegt“ lediglich daran vorbei).
Die Energiedichte einer gerichteten elektromagnetischen Strahlung entspricht bei vollständiger Absorption dem Strahlungsdruck, den diese Strahlung auf eine senkrecht gerichtete Fläche ausübt!
Im Gegensatz zum Fall der vollständigen Absorption, führt bei vollständiger Reflexion der Strahlung dieselbe Energiedichte zu einem doppelt so großen Strahlungsdruck, da der Impulsübertrag bei einer Kollision ja doppelt so groß ist:
\begin{align}
&\boxed{p_{St} = 2w} ~~~~~\text{gilt nur bei vollständiger Reflexion}
\end{align}
Ungerichtete Strahlung (Photonengas)
Beachte, dass diese Zusammenhänge zwischen dem Strahlungsdruck und der Energiedichte nur für eine gerichtete Strahlung gelten. Alle Photonen bewegen sich in diesen Fällen in eine gemeinsame Richtung. Somit nehmen auch alle Photonen an der Ausübung des Druckes teil.
Anders sieht die Situation aus, wenn es sich nicht mehr um eine gerichtete Strahlung sondern um eine völlig statistische Verteilung der Photonenbewegung handelt. Dies ist bspw. der Fall, wenn Strahlung in einem verspiegelten Hohlkörper betrachtet wird.

Die Photonen werden dann permanent an den Wänden reflektiert und es wird sich mit der Zeit eine völlig zufällige Photonenbewegung ausbilden. Aus der ursprünglich gerichteten Bewegung, bei der sich alle Teilchen auf die Wand zubewegten, werden im Mittel nun nur noch ein Sechstel in Richtung Wand unterwegs sein. Die restlichen Teilchen werden sich nach rechts bewegen, nach links, nach oben, nach unten oder sich von der Wand entfernen. Bei derselben Energiedichte (Photonendichte) beträgt der Strahlungsdruck bei einer solchen zufälligen Photonenbewegung nur ein Sechstel im Vergleich zu einem gerichteten Photonenstrahl:
\begin{align}
&\boxed{p= \frac{1}{6} \cdot p_{St} = \frac{1}{6}\cdot 2w = \frac{1}{3}w} ~~~~~\text{gilt nur eine ungeordnete Strahlung}
\end{align}
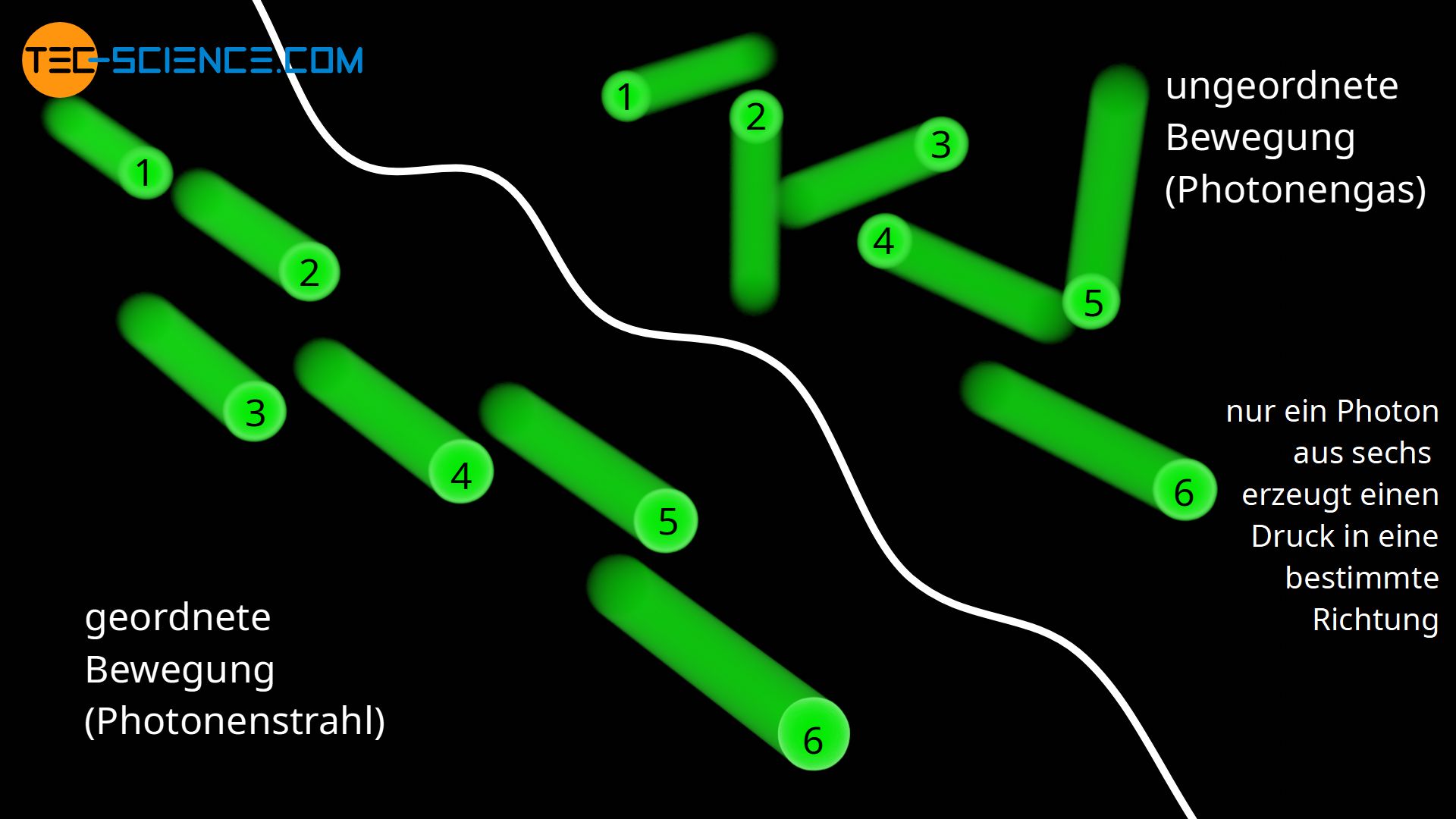
Die chaotische Bewegung der Photonen gleicht der Bewegung von Gasteilchen in Gasen. Aus diesem Grund bezeichnet man diese Art der ungeordneten Strahlung auch als Photonengas. Mithilfe der Betrachtung der Strahlung als Photonengas und des hergeleiteten Zusammenhangs zwischen Energiedichte und Strahlungsdruck lässt sich bspw. das Stefan-Boltzmann Gesetz für strahlende Körper herleiten.


