Schmid’sches Schubspannungsgesetz

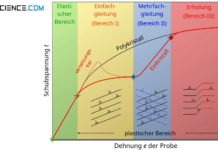
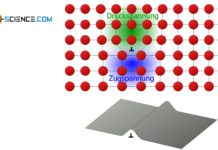
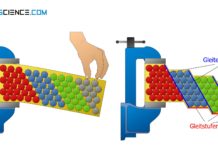
Äußere Normalspannungen induzieren im Inneren eines Materials Schubspannungen, die unter einem Winkel von 45° maximal werden.

Scherkraft

Wird ein Material unter Zug beansprucht, dann wird sich dieses bei zu hohen Zugkräften F₀ schließlich verformen. Wie im Abschnitt Grundlagen der Verformung erläutert, müssen hierfür Gitterebenen zum Abgleiten gebracht werden.

Für ein Abgleiten müssen Kräfte in geeigneter Weise in einer Gleitebene wirken, damit diese abgeschert werden können. Eine Kraft in der Gleitebene alleine reicht aber noch nicht aus. Denn innerhalb der Gleitebene muss die Kraft auch in Gleitrichtung orientiert sein. Wirkt bspw. in einer Gleitebene eine Scherkraft, welche jedoch senkrecht zur Gleitrichtung orientiert ist, dann wird sich diese Atomebene nicht ohne Weiteres abscheren lassen.

Nur Kräfte in Gleitrichtung sind für ein Abgleiten der Gitterebenen relevant!

Da die Kombination von Gleitebene und Gleitrichtung zusammen ein Gleitsystem bildet, gilt also folgendes:

Um einen Verformungsprozess auszulösen, müssen Kräfte in einem Gleitsystem wirken!

Deshalb stellt sich zunächst die Frage, wie sich anhand der äußeren Kraft F₀ die Kraft F in einem Gleitsystem gemäß dessen räumlicher Orientierung bestimmen lässt.

Hierfür ist also zum einen die räumliche Orientierung der Gleitebene relevant und zum anderen die Orientierung der Gleitrichtung innerhalb der Gleitebene. Beide Orientierungen werden jeweils über einen Winkel definiert.

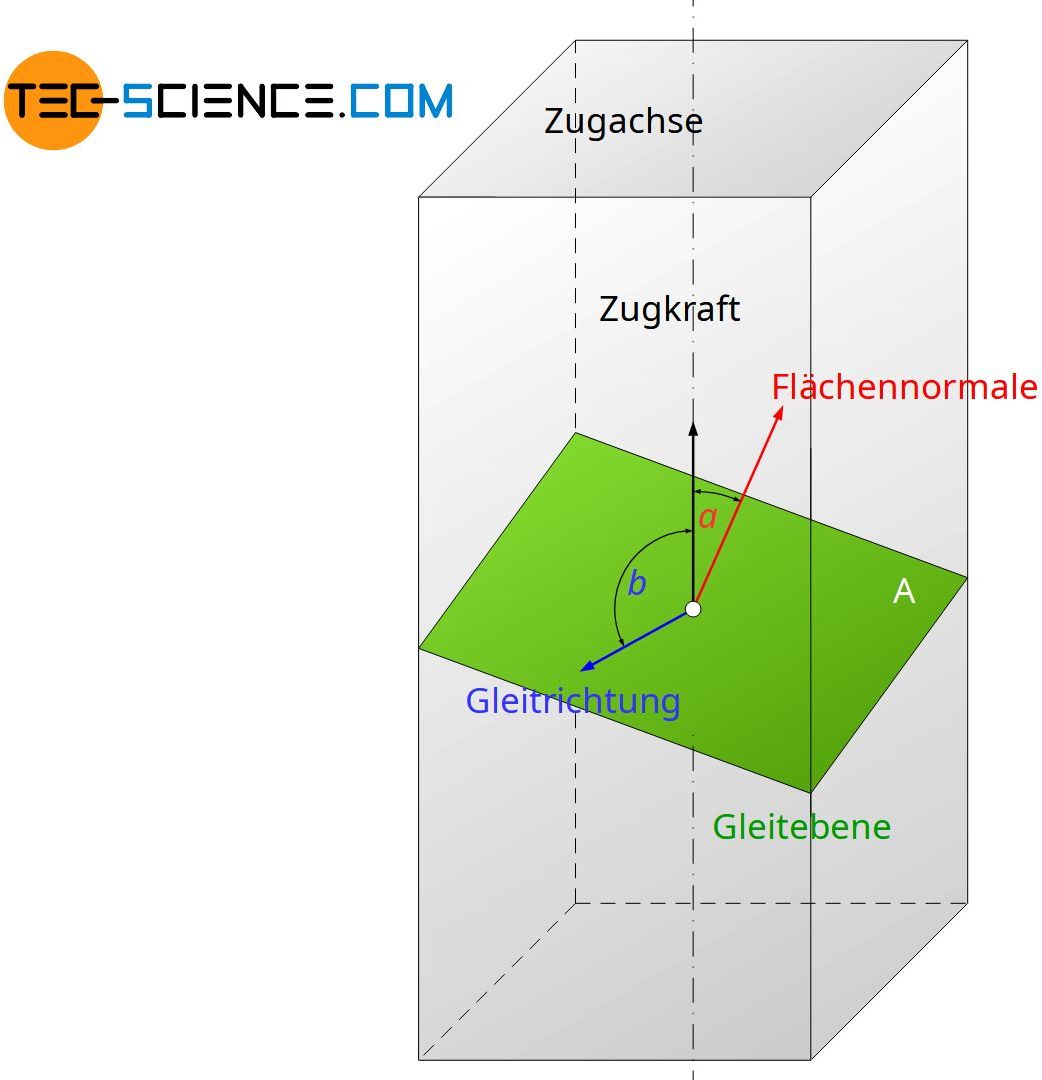
Der Winkel \(\alpha\) beschreibt dabei den Winkel zwischen äußerer Zugkraft F₀ und Flächennormalen der Gleitebene. Die Orientierung der Gleitrichtung wird analog als Winkel \(\beta\) zwischen Zugachse und Gleitrichtung definiert. Beachte, dass beide Winkel nur innerhalb bestimmter Grenzen unabhängig voneinander sind.

Zunächst wird die äußere Kraft F₀ in eine Komponente in Gleitrichtung zerlegt F_||. Dies geschieht über den Kosinus des Winkels \(\beta\):

\begin{equation}
\label{kraft}
F_{\parallel} = F_0 \cdot \cos(\beta)
\end{equation}

Offensichtlich erhält man eine größte Kraft in Gleitrichtung, wenn diese unter einem geringen Winkel \(\beta\) zur Zugachse orientiert ist. Die Gleitebene ist dann zwangsläufig sehr steil geneigt (großer Winkel \(\alpha\)). Mit einer solchen steilen Orientierung der Gleitebene nimmt jedoch auch dessen Fläche über den Querschnitt betrachtet zu.

Dies wiederum führt dazu, dass nun deutlich mehr Atombindungen zwischen den Gitterebenen „abgeschert“ werden müssen. Die abzuscherenden Gitterebenen „haften“ sozusagen stärker aneinander. In diesem Fall reicht dann selbst die größere Schubkraft aufgrund der überproportional angestiegenen Atomfläche („Haftkraft“) nicht aus, um die Ebene zum Abscheren zu bringen.

Es ist also nicht die Kraft alleine für einen Abgleitprozess entscheidend sondern ein möglichst günstiges Verhältnis von Kraft und Fläche (höchste Kraft pro Fläche)! Es ist deshalb stets die Schubspannung für einen möglichen Abgleitprozess zu betrachten.

Schubspannung

Der Quotient aus Schubkraft F_|| (in Gleitrichtung) und Gleitebenenfläche A ergibt die für den Abgleitprozess relevante Scherspannung \(\tau\):

\begin{equation}
\label{schubspannung}
\tau=\frac{F_{\parallel}}{A}
\end{equation}

Somit muss neben der vom Winkel \(\beta\) abhängigen Schubkraft F_|| auch die Abhängigkeit der Gleitebenenfläche vom Winkel \(\alpha\) bekannt sein. Wird die Querschnittsfläche der Probe mit A₀ bezeichnet, dann ergibt sich die Gleitebenenfläche A wie folgt anhand des Winkels \(\alpha\):

\begin{equation}
\label{flaeche}
A=\frac{A_0}{\cos(\alpha)}
\end{equation}

Wird Gleichung (\ref{flaeche}) und Gleichung (\ref{kraft}) in Gleichung (\ref{schubspannung}) eingesetzt, dann gilt für die Schubspannung \(\tau\) in Gleitrichtung einer beliebig geneigten Gleitebene:

\begin{align}
\label{a}
&\tau=\frac{F_{\parallel}}{A} = \frac{ F_0 \cdot \cos(\beta) }{ \tfrac{A_0}{\cos(\alpha)}} =  \frac{F_0}{A_0}\cdot \cos(\alpha) \cdot \cos(\beta) \\[5px]
\end{align}

Der Ausdruck \(\frac{F_0}{A_0}\) in Gleichung (\ref{a}) entspricht gerade der von außen aufgebrachten Normalspannung \(\sigma_0\). Damit lässt sich schließlich folgender Zusammenhang zwischen der von außen anliegenden Normalspannung \(\sigma_0\) und der in einem Gleitsystem induzierten Schubspannung  \(\tau\) herstellen:

\begin{align}
\label{s}
&\boxed{\tau = \sigma_0 \cdot \cos(\alpha) \cos(\beta)} ~~~~~\text{Schmid’sches Schubspannungsgesetz} \\[5px]
\end{align}

Gleichung (\ref{s}) wird auch Schmid’sches Schubspannungsgesetz genannt. Darin wird der Geometriefaktor \(\cos(\alpha) \cos(\beta)\) häufig auch als Schmid-Faktor \(m\) bezeichnet:

\begin{align}
\label{schmid-faktor}
&\boxed{\tau = \sigma_0 \cdot m} ~~~~~\text{mit}~~~~~\boxed{m=\cos(\alpha) \cos(\beta)} \\[5px]
\end{align}

Der Schmid-Faktor beschreibt den Zusammenhang zwischen äußerer Normalspannung und der in einem Gleitsystem hervorgerufenen Schubspannung!

Kritische aufgelöste Schubspannung

Wird in einem Gleitsystem als erstes eine bestimmte kritische Schubspannung überschritten (in jenem Gleitsystem mit dem größten Schmid-Faktor), dann beginnen dort die Ebenen abzugleiten bzw. Versetzungen durch den Kristall zu wandern. Der Verformungsprozess setzt ein.

Beachte, dass sich die kritischen Schubspannungen also nicht auf die „bloße“ Schubspannung in einer Gleitebene beziehen sondern auf jenen Anteil der in Gleitrichtung zeigt. Deshalb werden diese kritische Schubspannungen auch als kritische „aufgelöste“ Schubspannungen bezeichnet. Der Begriff „aufgelöst“ meint dabei letztlich die in Gleitrichtung zerlegte („aufgelöste“) Schubspannung.

Um Gleitebenen zum Abscheren zu bringen, müssen in einem Gleitsystem (insb. in Gleitrichtung) bestimmte kritische aufgelöste Schubspannungen überschritten werden!

Der Unterschied zwischen der „bloßen“ Schubspannung in einer Gleitebene und der aufgelösten Schubspannung in Gleitrichtung soll an einem kurzen Zahlenbeispiel erläutert werden. Hierzu wird eine Gleitebene betrachtet die unter einem Winkel von \(\alpha\) = 15° geneigt ist.

Wird nun von außen eine Normalspannung von \(\sigma_0\) = 400 N/mm² aufgebracht, dann wirkt in dieser Gleitebene eine Schubspannung von  \(\tau_{E}\) = 100 N/mm². Wäre die Gleitrichtung in diesem Fall in einem Winkel von \(\beta\) = 75° zur Zugachse orientiert, dann würden die 100 N/mm² tatsächlich auch der Schubspannung in Gleitrichtung entsprechen.

Ist die Gleitrichtung in der Gleitebene hingegen im Winkel von \(\beta\) = 80° zur Zugachse orientiert, dann wird in dieser Gleitrichtung nur eine Schubspannung von \(\tau_{R}\) = 67 N/mm² wirken. Diese in Gleitrichtung aufgelöste Schubspannung ist für die Beurteilung eines Abgleitens relevant und nicht die in der Ebene wirkende Spannung von 100 N/mm²!

Maximale aufgelöste Schubspannung

Es stellt sich die Frage, wie ein Gleitsystem räumlich orientiert sein muss, um dort eine möglichst große Schubspannung zu erhalten (maximaler Schmid-Faktor). Ist es vielleicht sogar möglich, ein Gleitsystem so zu orientieren, dass die gesamte äußere Normalspannung in Gleitrichtung aktiv ist?

Hierfür muss Gleichung (\ref{schmid-faktor}) näher betrachtet werden. Zunächst erreicht zwar der Ausdruck \(\cos(\alpha)\) für \(\alpha\) = 0 den Maximalwert 1, jedoch beträgt in diesem Fall \(\beta\) unweigerlich 90° und damit \(\cos(\beta)\) = 0. Der Schmid-Faktor ist somit null. In Gleitebenen die senkrecht zur Zugachse ausgerichtet sind, wirkt folglich keine Scherspannung!

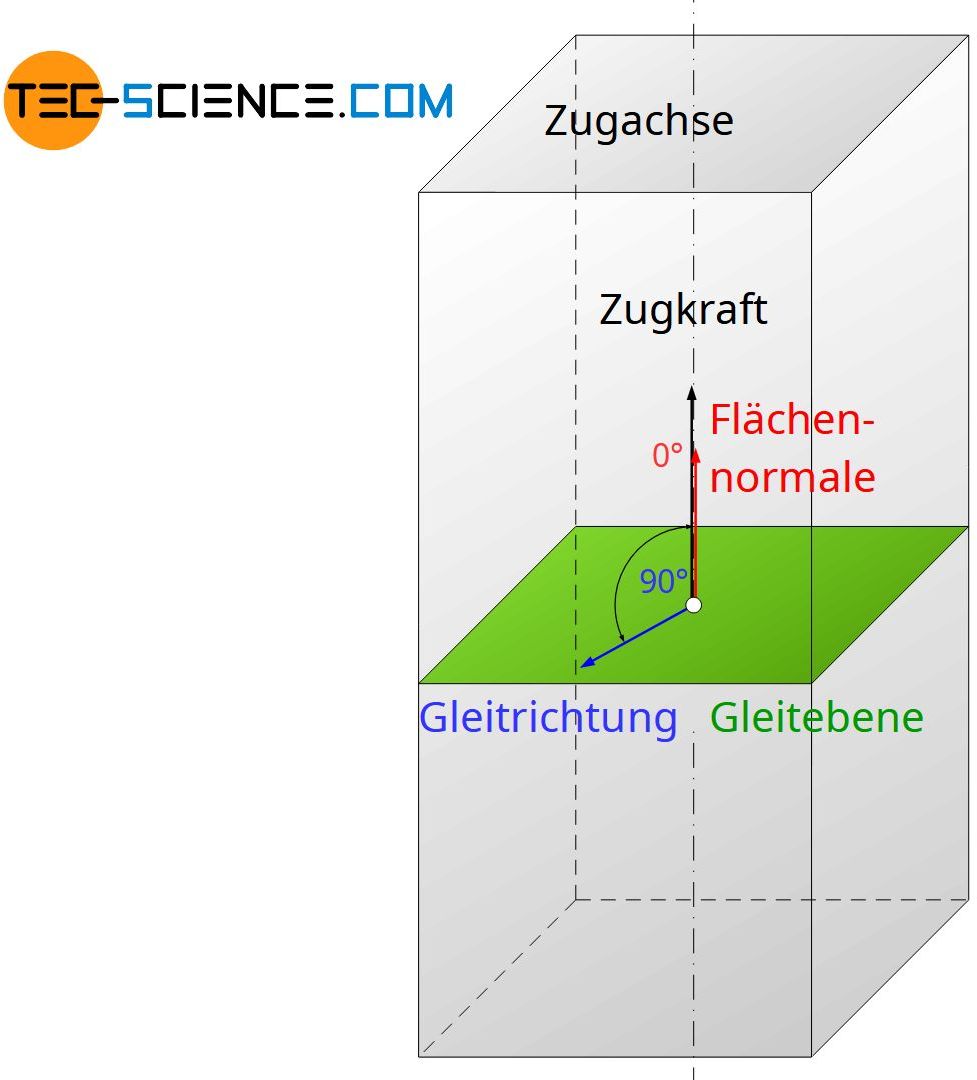
Auch für den umgekehrten Extremfall, wenn die Gleitebenen parallel zur Zugachse ausgerichtet sind (\(\alpha\)=90°), ergibt sich keine Spannung in der Gleitebene, da dann unweigerlich gilt \(\cos(\alpha)\) = 0!

Tatsächlich werden die größten Schubspannungen in einer Gleitebene unter einem Winkel von \(\alpha\)=45° zu finden sein. Die maximal wirkende (aufgelöste) Schubspannung ergibt sich dann, wenn die Gleitrichtung in dieser 45°-geneigten Gleitebene direkt „nach oben“ gerichtet ist. Der Winkel \(\beta\) beträgt in diesem Fall ebenfalls 45° (Beachte, dass die beiden Winkel nicht völlig unabhängig voneinander gewählt werden können!). Der Schmid-Faktor erreicht in diesem Idealfall 0,5. Dies entspricht folglich dem maximal möglichen Wert des Schmid’schen Orientierungsfaktors:

\begin{align}
&m_{max}=\cos(45°) \cos(45°) = 0,5 \\[5px]
&\boxed{m \le 0,5} \\[5px]
\end{align}

Die maximal aufgelösten Scherspannungen sind also im Idealfall halb so groß wie die äußeren Normalspannungen.

In Gleitsystemen die unter einem Winkel von 45° geneigt sind entstehen die größten Scherspannungen. Sie betragen die Hälfte der äußeren Normalspannungen!

Dies ist auch der Grund weshalb spezielle orientierte Einkristalle im Zugversuch Gleitstufen unter einem Winkel von 45° zur Zugachse aufweisen. Nähere Informationen hierzu finden sich im Beitrag Verformung am Einkristall wieder.